Laboratórium 1 - 2. Mérés: Alapmérések

Beugró kérdések kidolgozása

Ezt a részt még aktualizálni kell, meg valami pofásabb formára kéne hozni. Az első kérdéseknél megadtam az alapot, a többit is így kéne megformázni - Régi wikioldal

1. Egy digitális feszültségmérő 2 V-os méréshatárában 0.050 V-ot mutat. Mekkora a kvantálásból származó hiba?

Kvantálási hiba: digitális műszer utolsó számjegyének/digitjének hibája, százalékban a mért értékre vonatkoztatva. Itt: $\frac{0,001}{0,050}=2\mathrm{\%}$

2. Egy Deprez-műszer segítségével soros Ohm-mérőt építünk. Mekkorára válasszuk az Rs soros ellenállást, ha a mérendő ellenállás névleges értéke R = 1 kOhm, és maximális mérési pontosságot szeretnénk elérni? Mekkora a mérés bizonytalansága abban az esetben, ha a műszer osztálypontossága 0.5%?

o.p. Analóg műszer kitérésének hibája a maximális kitérésre vonatkoztatva, százalékban [angolul accuracy], esetleg % jel nélkül jelezve [angolul class] : $\frac{h_{abs}}{x_{\text{max}}}\cdot 100$ Ebből relatív (a mért értékre vonatkoztatott) mérési hibát így kapunk: $\frac{o.p.}{100}\cdot \frac{x_{max}}{x_{mert}}$

Hogyan mérünk egy árammérővel, és egy soros ellenállással ellenállást ? Megmérjük először csak a soros ellenálláson átfolyó áramot: $I_{max}=\frac{U}{R_s}$, majd megmérjük a mindkét ellenálláson átfolyó áramot: $I=\frac{U}{R_s+R}$. A fenti egyenletekből: $R=R_s(\frac{I_{max}}{I}-1)$ illetve amire még később szükség lesz: $\frac{I_{\max }}{I}=\frac{R_s+R}{R_s}$ Majd ezek tudatában elkezdjük addig variálni az utóbbit, amíg benne nem lesz az osztálypontosság (ugyanis más mérési hibát nem ismerünk). R hibája az árammérés hibájára vonatkoztatva (Amper/Ohm a mértékegysége, de tök mindegy). $\frac{\mathrm{\Delta }R}{\mathrm{\Delta }I}=-R_s\frac{I_{max}}{I^2}\Rightarrow \mathrm{\Delta }R=-R_s\frac{I_{max}}{I}\frac{\mathrm{\Delta }I}{I}=-R_s\frac{R_s+R}{R_s}\frac{\mathrm{\Delta }I}{I}=-(R_s+R)\frac{\mathrm{\Delta }I}{I}$. R relatív hibája : $\frac{\mathrm{\Delta }R}{R}=\frac{-(R_s+R)\frac{\mathrm{\Delta }I}{I}\cdot \frac{I_{max}}{I_{max}}}{R}=\frac{-(R_s+R)\stackrel{o.p.}{\overbrace{\frac{\mathrm{\Delta }I}{I_{max}}}}\cdot \stackrel{I_{max}/I}{\overbrace{\frac{R_s+R}{R_s}}}}{R}=-\frac{(R_s+R{)}^2}{R_{s}R}\cdot o.p.$

Ennek kell a minimumát keresni $R_s$ szerint (for advanced users: az az $R_s$ érték, ahol az $R_s$ szerinti derivált nulla: )

$-o.p.\left(\frac{2(R_s+R)R_{s}R-R(R_s+R{)}^2}{{\left(R_{s}R\right)}^2}\right)=0$ Nevezővel beszorozhatunk $-o.p.\left(R(R_s+R)\cdot (2R_s-(R_s+R)\right)=0$ $R(R_s+R)$ sosem lesz nulla $-o.p.\left((2R_s-(R_s+R)\right)=0\iff R_s\equiv R$ Ha $R_s=R$ akkor $\left|\frac{\mathrm{\Delta }R}{R}\right|=\frac{(R_s+R{)}^2}{R_{s}R}\cdot o.p.=4\cdot o.p.$

Egy Deprez-rendszerű feszültségmérővel egyenfeszültséget mérünk. A műszer skálabeosztása lineáris, végkitérése 100 osztás, méréshatára 10 V, osztálypontossága 1%. A műszer kitérése 65 osztás. Mekkora a mért feszültség értéke, és a mérés bizonytalansága?

6,5V-ot mértünk, és az osztálypontosság fenti definíciója alapján $\frac{\mathrm{\Delta }U}{U}=\frac{o.p.}{100}\cdot \frac{x_{max}}{x_{mert}}=\frac{10V}{6,5V}\cdot 0,01=1,5\mathrm{\%}$

Rajzolja fel az általános Wheatstone-híd kapcsolását, és adja meg a kiegyenlítés feltételét! Egymással átellenesen: párhuzamos(soros($R_1$, $R_2$),soros($R_3$, $R_4$)). A híd kimeneti feszültségét a bemeneti feszültségből feszültségosztással kapjuk: $U_{ki}=U_{be}\left(\frac{R_2}{R_1+R_2}-\frac{R_4}{R_3+R_4}\right)$. Kiegyenlített a híd, ha $U_{k}i=0$, azaz $R_2{R}_3=R_1{R}_4$.

5. 1 V csúcsértékű 50 Hz frekvenciájú szimmetrikus háromszögjelet mérünk Deprezműszerrel. A méréshez aktív egyutas egyenirányítót használunk. A kapcsolásban használt ellenállások mindegyike R = 1 kOhm +/- 1%, a diódafeszültség Ud = 0.6 V a műszer végkitérése 1 V, és osztálypontossága 0.5%, a műveleti erősítő ideálisnak tekinthető.

• Adja meg a kapcsolási rajzot, és a műszer által mért jelalakot!
• Milyen értéket mutat a műszer?
• Adja meg mérés eredő bizonytalanságát, az összes hibakomponens "worst case" alapú összegzésével!

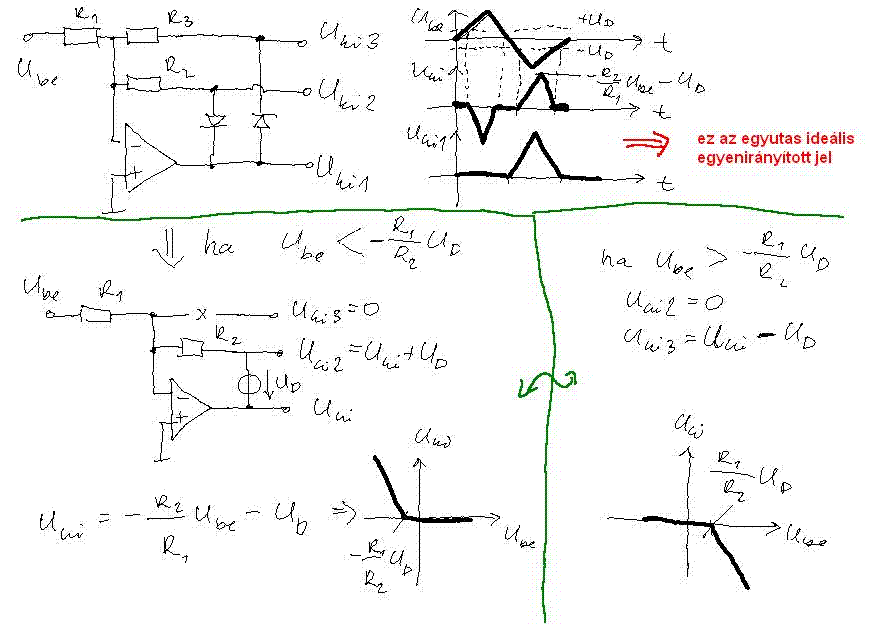
Valamelyik félhullám esetén valamelyik dióda nem vezet, tehát szakadásnak vehető, a másik dióda vezet, tehát egy 0,6V-os generátornak tekinthető. Ekkor felírható az ideális erősítő invertáló bemenetére a csomóponti áram: $\frac{U_{be}}{R_1}+\frac{U_{ki1}}{R_2}=0\Rightarrow U_{ki1}=-\frac{R_2}{R_1}{U}_{be}-0,6V$ Látszik, hogy invertáló erősítő, és erősítése 1 lesz, ha az ellenállások megegyeznek.

A műszer $U_{k}i(t)$ absz. középértékét méri (integrálás, háromszögek területe..): $\frac{1}{T}\underset{0}{\overset{T}{\int }}\left|u_{ki1}(t)\right|dt=\frac{1}{T}\cdot 2\cdot \frac{1V\cdot T/4}{2}=0,25V$ -ot mutat a műszer. $\frac{\mathrm{\Delta }{U}_{ki1}}{U_{ki1}}=\frac{\left|{\mathrm{\Delta }{U}_{ki1}|}_{R_1}\right|+\left|{\mathrm{\Delta }{U}_{ki1}|}_{R_2}\right|}{\left|U_{ki1}\right|}=\frac{\left|-\frac{R_2}{R_1^2}{U}_{be}\mathrm{\Delta }{R}_1\right|+\left|-\frac{1}{R_1}{U}_{be}\mathrm{\Delta }{R}_2\right|}{\left|-\frac{R_2}{R_1}{U}_{be}\right|}=\frac{\frac{R_2}{R_1}\frac{\mathrm{\Delta }{R}_1}{R_1}+\frac{R_2}{R_1}\frac{\mathrm{\Delta }{R}_2}{R_2}}{R_2/R_1}=\frac{\mathrm{\Delta }{R}_1}{R_1}+\frac{\mathrm{\Delta }{R}_2}{R_2}=2\mathrm{\%}$

Ehhez még hozzájön az osztálypontosságból adódó hiba: $\frac{U_{max}}{U_{ki1}}\cdot o.p.=\frac{1V}{0,25V}\cdot 1\mathrm{\%}=4\mathrm{\%}$

Így a mérés bizonytalansága 6%.

Digitális multiméterrel egyenfeszültséget mér. A műszer végkitérése 19.999 V, a mutatott érték 12.345 V. Adja meg a mérés pontosságát az alábbi specifikációs adatok, és a mutatott érték alapján! DC Voltmérés pontossága : +/- (0.05% o.v. + 0.01% o.r.) o.v. = of value (mért mennyiségre) o.r. = of range (végkitérésre) $h=\pm (o.v.+o.r.\frac{U_{mert}}{U_{max}}+\frac{0,001}{U_{mert}}\cdot 100\mathrm{\%})=\pm 0,074\mathrm{\%}$

Rajzolja fel a dual-slope átalakító blokkvázlatát és ismertesse a működését! Fejezze ki a mért feszültséget!

10 V effektív értékű szabályos valamilyenjelet mérünk akármilyenérték-mérő AC voltmérővel. Mekkora feszültséget mutat a műszer? Általában minden analóg AC mérőműszer a szinuszos jel eff. értékét jelzi ki helyesen. Akármilyenérték-mérő műszer az $U$ amplitudójú valamilyen jel $Ux$ akármilyenértékét méri, és egy ilyen $Ux$ akármilyen értékkel rendelkező szinuszos jel $U_{eff}$ effektív értékét jelzi ki. Például: 10 V effektív értékű szabályos háromszögjel amplitudója $\sqrt{3}\cdot 10V$ Absz. középérték-mérővel a $\sqrt{3}\cdot 10V$ amplitúdójú szab. hsz. jel absz.k-értékét mérjük, azaz $\frac{\sqrt{3}\cdot 10V}{2}$ -ot. Az ekkora absz.középértékkel rendelkező szinuszos jel (amplitudója $\frac{\pi }{2}\cdot \frac{\sqrt{3}\cdot 10V}{2}$, tehát) effektív értéke $\sqrt{2}\cdot \frac{\pi }{2}\cdot \frac{\sqrt{3}\cdot 10V}{2}$ Alább egy táblázat mutatja, hogy adott amplitudójú jel esetén az adott értéket mérő eszköz mit mér (nyílván az adott értéket), mit mutat (a hosszú mondat fent), és a mutatott értéket milyen *szorzó*val kell megszorozni, hogy a jel effektív értékét kapjam meg.

Jelalak	Effektív érték			Abszolút középérték			Csúcsérték
	mér	mutat	szorzó	mér	mutat	szorzó	mér	mutat	szorzó
Szinusz	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$	$1$	$\frac{2}{\pi }$	$\frac{1}{\sqrt{2}}$	$\frac{\pi }{2\sqrt{2}}$	$1$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$
Háromszög	$\frac{1}{\sqrt{3}}$	$\frac{1}{\sqrt{3}}$	$1$	$\frac{1}{2}$	$\frac{\pi }{4\sqrt{2}}$	$\frac{\pi }{2\sqrt{2}}$	$1$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$
Négyszög	$1$	$1$	$1$	$1$	$\frac{\pi }{2\sqrt{2}}$	$\frac{\pi }{2\sqrt{2}}$	$1$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$

Rajzoljon fel egy egyszerű feszültségváltót, adja meg a primer és a szekunder feszültség kapcsolatát! Egy transzformátor, bemenetén feszültség-generátor, kimenetén $Z_t>0$ terhelés. $\frac{U_2}{U_1}=\frac{N2}{N1}$

Rajzoljon fel egy egyszerű áramváltót, adja meg a primer és a szekunder áram kapcsolatát! Egy transzformátor, bemenetén áram-generátor, kimenetén $Z_t<\mathrm{\infty }$ terhelés. $\frac{I_2}{I_1}=\frac{N1}{N2}$

10 V effektív értékű szabályos négyszögjelet mér abszolútértékmérő AC voltmérővel. Mekkora feszültséget mutat a műszer?(lásd a 8. kérdést) 10VRMS négyszögjel 10VPP csúcsértékű, és ennek az abszolútértékét mérjük, ami szintén 10V. 10V abszolútértékű szinusz jel $\frac{\pi }{2}\cdot 10V$ amplitudóval, illetve $\frac{\pi }{2\sqrt{2}}\cdot 10V$ effektív értékkel bír. Utóbbit mutatja a műszer, azaz 11,1 V-ot

1000 Ohm értékű ellenállást készítünk egy 900 ohm 1%-os, és egy 100 Ohm 10%-os ellenállás sorba kapcsolásával. Mekkora lesz az ellenállás valószínű hibája? $\frac{\mathrm{\Delta }R}{R}=\sqrt{{\left({\frac{\mathrm{\Delta }R}{R}|}_{R_1}\right)}^2+{\left({\frac{\mathrm{\Delta }R}{R}|}_{R_2}\right)}^2}=\sqrt{{\left(\frac{\mathrm{\Delta }{R}_1}{R_1+R_2}\right)}^2+{\left(\frac{\mathrm{\Delta }{R}_2}{R_1+R_2}\right)}^2}=\sqrt{{\left(\frac{9\mathrm{\Omega }}{1000\mathrm{\Omega }}\right)}^2+{\left(\frac{10\mathrm{\Omega }}{1000\mathrm{\Omega }}\right)}^2}=1,35\mathrm{\%}$

Rajzoljon fel egy Graetz egyenirányító kapcsolást, és jelölje meg a váltakozó-áramú bemenetet, és az egyenáramú kimenetet! Hogy jegyezzük meg, merre néz a dióda ? :) A,B,C,D négyzet, A,C a bemenet. Ha A-ra + félhullám jön, akkor ezt az egyik kimeneten le kell szedni, legyen ez a B kimenet (tehát A->B az egyik dióda), ugyanekkor nem szabad, hogy D kimeneten a + félhullám látszódjék, ezért ott a dióda fordítva van (A<-D). Ha C-re jön a + félhullám, akkor ezt megintcsak B-n lássuk (C->B), de D-n ne (C<-D). (vajon most bizonyítottam-e mindkét irányt ? :-)

Négy db különböző értékű és pontosságú ellenállást kapcsolunk párhuzamosan: 1 db. 1 kOhm 0.01%-os, 1 db. 10 kOhm 0.1%-os 1 db. 100 kOhm 1%-os 1 db. 1 MOhm 10% -os ellenállást. Mekkora lesz az eredő ellenállás értéke, és hibája, a hibakomponensek valószínűségi összegzésével? Nem éri meg eredő ellenállással bajlódni, inkább vegyük a vezetéseket, és számoljunk azokkal, tudván azt, hogy $\frac{\mathrm{\Delta }G}{G}=-\frac{\mathrm{\Delta }R}{R}$. Az eredő vezetés értéke $G=(1+0,1+0,01+0,001)mS=1,111mS$, így az eredő ellnállás ennek reciproka: $R=900,09\mathrm{\Omega }$. A hiba $\frac{\mathrm{\Delta }G}{G}=\sqrt{\sum _{i=1}^4{\left({\frac{\mathrm{\Delta }G}{G}|}_{G_i}\right)}^2}=\sqrt{\sum _{i=1}^4{\left(\frac{\mathrm{\Delta }{G}_i}{G}\right)}^2}=\sqrt{{\left(\frac{1\cdot 0,01\mathrm{\%}}{1,111}\right)}^2+{\left(\frac{0,1\cdot 0,1\mathrm{\%}}{1,111}\right)}^2+{\left(\frac{0,01\cdot 1\mathrm{\%}}{1,111}\right)}^2+{\left(\frac{0,001\cdot 10\mathrm{\%}}{1,111}\right)}^2}=0,018\mathrm{\%}$

1 V effektív értékű szinuszjelhez 1 V egyenfeszültséget adunk. Mekkora lesz az így nyert feszültség effektív értéke? $U_{eff}=\sqrt{\sum _{i=0}^n{U}_i^2}=\sqrt{1^2+1^2}=1,41V$

Egy mérünk Deprez-műszer segítségével párhuzamos Ohm-mérőt építünk. Mekkorára válasszuk az RP párhuzamos ellenállást, ha a mérendő ellenállás névleges értéke 10 kOhm, és maximális mérési pontosságot szeretnénk elérni? Mekkora a mérés hibája abban az esetben, ha a műszer osztálypontossága 1%? Lásd 2. kérdés. Csak itt párhuzamosan van kapcsolva a mérendő és a "párhuzamos" ellenállás, valamint a Deprez-műszer, voltmérő állásban. Ha így volna, akkor az jönne ki eredményül, hogy $R_p=0$ választással 0 hibájú mérést végezhetnénk. Ez elég örömteli, csakhogy 0 ellenálláson mért feszültség nem nagyon látszik a műszeren, arról nem beszélve, hogy a táp meg elfüstölhet, ha rövidre zárják a pontos mérés érdekében. A mérési elrendezés ezért egyszer áll a párhuzamosan kapcsolt ellenállásokból, majd csak $R_p$-ből, és Deprez-műszer méri mindkét esetben az eredőáramot. $R=R_p\frac{I_{max}/I}{1-I_{max}/I}$ illetve amire még később szükség lesz: $\frac{I_{max}}{I}=\frac{R}{R_p+R}$ Mivel ez ilyen bonyolult, érdemes mindent újraszámolni vezetésre, és akkor sztem ugyanolyan alakú lesz, mint a 2. feladat (vezetés relatív hibája ugyanannyi, mint az ellenállásé).

Egy zsebtelep üresjárási (terhelés nélküli) feszültsége UO = 9.2500 V, 1 kOhm-os ellenállással terhelve a feszültsége U1 = 9.0000 V-ra változott. Mekkora a telep belső ellenállása? Mekkora az feszültségmérések hibája, ha méréseket olyan digitális multiméterrel végeztük, melynek a gépkönyvében az alábbi adatokat találjuk: DC feszültségmérés pontossága: +/- (0.05% o.v. + 0.005% o.r)

Egy oszcilloszkóp bemenete 1 MOhm ellenállással és a vele párhuzamosan kapcsolódó kapacitással modellezhető. A mérendő jelet egy 5 MOhm-os soros ellenálláson keresztül vezetjük az oszcilloszkóp bemenetére. Mekkora kapacitású kondenzátort kell a soros ellenállással párhuzamosan kapcsolni ahhoz, hogy a jel hozzávezetés frekvenciafüggetlen legyen?

Adott egy fojtótekercs, melynek 30 Ohm ellenállása és 400 Ohm a reaktanciája. 40 V, 50 Hz tápfeszültség esetén mekkora az áram abszolút értéke és fázisszöge? Mekkora az áram valós és képzetes összetevője?

Számítsa ki egy 24 V-os 40 W teljesítményű izzólámpa üzemi áramát, és ellenállását! Becsülje meg mekkora lehet a hideg ellenállása!

Rajzolja fel egy három voltmérős teljesítménymérés kapcsolási vázlatát!

Rajzolja fel egy három voltmérős teljesítménymérés fazor ábráját!