„Szerkesztő:Nagy Vilmos/Jelek Gyakorlatjegyzet - 2017 (ősz)” változatai közötti eltérés
→3. feladat: mátrix teszt |
|||
| 160. sor: | 160. sor: | ||
Számoljuk ki a rendszer impulzusválaszát! | Számoljuk ki a rendszer impulzusválaszát! | ||
A számolás módja az elődásjegyzetben van részletezve, ide csak a fontosabb rész-eredményeket vésem le | A számolás módja az elődásjegyzetben van részletezve, ide csak a fontosabb rész-eredményeket vésem le. | ||
==== A, B, C, D mátrixok ==== | |||
<math>\underline{\underline{A}} = \begin{bmatrix} | <math>\underline{\underline{A}} = \begin{bmatrix} | ||
0 & 1 \\ | 0 & 1 \\ | ||
| 172. sor: | 173. sor: | ||
<math>\underline{C}^T = \begin{bmatrix} 0 & 1\end{bmatrix}</math> | <math>\underline{C}^T = \begin{bmatrix} 0 & 1\end{bmatrix}</math> | ||
<math>d = 1</math> | <math>d = 1</math> | ||
==== Saját értékek, Lagrange Mátrixok ==== | |||
<math>\lambda_1 = -0.1</math> | |||
<math>\lambda_2 = -0.5</math> | |||
<math>\underline{\underline{L_1}} = \begin{bmatrix} | |||
1.25 & 2.5 \\ | |||
-0.125 & -0.25 | |||
\end{bmatrix}</math> | |||
<math>\underline{\underline{L_2}} = \begin{bmatrix} | |||
-0.25 & -2.5 | |||
0.125 & 1.25 | |||
\end{bmatrix}</math> | |||
<math>\underline{C}^T \cdot \underline{\underline{L_1}} \cdot \underline{B} = -0.125</math> | |||
<math>\underline{C}^T \cdot \underline{\underline{L_2}} \cdot \underline{B} = 1.625</math> | |||
==== Impulzusválasz ==== | |||
<math>h[k] = \delta[k] + \epsilon[k-1] \cdot (-0.125 \cdot (-0.1^k) + 1.625 \cdot (-0.5^k))</math> | |||
A lap 2017. szeptember 24., 17:47-kori változata
A félévben tervezem letisztázni ide a Jelek (Rendszerelmélet) jegyzeteimet - lehetőleg valami olyan formában, ami az első ZH előtt segít rendesen összefoglalni az anyagot, s egy ponthatáros kettest összehoz.
Ha a félév végéig sikerül rendesen csinálnom (igyekszem :-)), s legalább az első ZHig (~hetedeik hét) le van tisztázva az anyag, akkor közkincsé teszem, s mehet a Rendszerelmélet lap alá. Addig viszont szeretném a személyes játszóteremnek meghagyni (nemhiába szerkesztői subpage ez), s bármit hezitálás nélkül visszavonok, ami nem tetszik. Ha hibát találsz, vagy kérdésed van, a Vitalapon állok rendelkezésre. (vagy a vilmos.nagy@outlook.com email címen)
Ez az oldal a gyakorlaton elhangzott feladatokat, s azok megoldásait tartalmazza - már, amit felfogtam belőle. Az előadásjegyzetemet erre találod: Szerkesztő:Nagy_Vilmos/Jelek_Előadásjegyzet_-_2017_(ősz)
1. Gyakorlat
Periodicitás vizsgálata
Diszkrét idejű jelek
Adott . Hogyan számoljuk ki, hogy periodikus-e?
Felírjuk az periodicitás definícióját, majd számolunk:
Az így kapott L értéknek definíció szerint egész számnak kell lennie. Három eset lehet a számolás végén:
- Az L egész. Örülünk, a jel periodikus.
- Az L racionális tört. Szorozzuk fel, hogy egész legyen (erre van a képletben az n), s örülünk, a jel periodikus.
- Az L irracionális tört. Ebből sehogy nem lesz egész, a jel nem periodikus.
Általánosságban a összefüggést érdemes megjegyezni, majd abból számolni.
Feladatok
Peridokusak-e az alábbi jelek? Amennyiben igen, mi a periódusideje?
Nem.
Erre semmilyen olyan n-t nem tudunk mondani, hogy L egész legyen.
Kis számolással beláthatjuk, hogy a diszkrét idejű jelek csak akkor lesznek periodikusak, ha a k racionális többszöröse.
Igen.
Nem.
Igen.
Nem.
Igen.
Folytonos idejű jelek
Folytonos idejű jelek periodicitását ugyanúgy vizsgáljuk, mint a diszkrét idejű jeleknél. Az egyetlen különbség, hogy a folytonos idejű jeleknél a periódusidő nem szükségszerűen egész, hanem lehet racionális szám is: .
Feladatok
Peridokusak-e az alábbi jelek? Amennyiben igen, mi a periódusideje?
Ilyen jeleknél, amik több periodikus jel szuperpozíciója, az egyes részeinek periódusidejét számoljuk ki, majd ezen periódusidők legkisebb közös többszöröse lesz a szuperponált jel periódusideje.
Az jel három jel szuperpozíciója. Ezek külön, külön:
- 1.
- 2.
- 3.
Ebből az utolsó triviálisan periodikus, periódusideje tulajdonképpen bármelyik racionális szám. A másik kettőről meg megtanultuk középiskolában, hogy periodikusak, periódusidejük:
Ezek alapján az eredeti jel periodikus, periódusideje: .
A fentiek alapján periodikus, periódusideje: .
Rendszer válaszának kiszámolása lépésenként
Diszkrét idejű jelek
Adott a öszefüggés. Továbbá tudjuk, hogy , s . Számoljuk ki az y értékeit különböző k értékekre.
Az előadásvázlatban van hasonló példa. Az egészet -ra rendezve kapunk egy egyszerű összefüggést. Mivel tudjuk az -et, így az triviálisan számolható. Ezek után a következő, majd a következő, majd az azt követő y érték is. Valahogy így:
| k | u | y |
|---|---|---|
| -1 | 0 | 5 |
| 0 | 2 | 2 |
| 1 | 2 | 12.4 |
| 2 | 2 | ... |
A gyakorlaton ezt még felrajzoltuk egy grafikonra. Két dolgot jegyeztünk meg:
- A diszkrét értékeket nem kötjük össze!
- A tengelyek legyenek elnevezve!
A fenti módszer hátránya, hogyha szeretném tudni a értékét, akkor ahhoz ki kell számolni a értékét, és így tovább összes korábbi értéket is.
Folytonos idejű jelek
Folytonos idejű jelek is lehetnének hasonlóan számolhatóak, de ott a megfelelő lépésköz sokkal nehezebben meghatározható (gondolj a Taylor polinommal való közelítésre).
2. Gyakorlat
Itt nem voltam, sry. Aki akarja, pótolja nyugodtan ide
3. Gyakorlat
1. feladat
Moriczkának 1000 pénze van. 10% éves kamatra beteszi a bankba, ahol azt évente tőkésítik.
- Mennyi pénze lesz Móriczkának 1-2-3 év múlva? Számold ki kézzel!
- Rajzolj jelfolyam hálózatot.
2. feladat
Az előadásjegyzetben pedzegetett hallgatós példa, csak más számokkal. A fent linkelt előadás-jegyzetem legelején megtalálod, nem részletezem itt.
3. feladat
Adott az alábbi rendszer:
(szerk.: Remélem nem csesztem el benne semmit, az x[k], meg x[k+1] jelölés nem tuti. http://draw.io -n rajzolva, forrás itt: https://drive.google.com/open?id=0BzSJOKSJE6qqWGNHcDE2MDkzems )
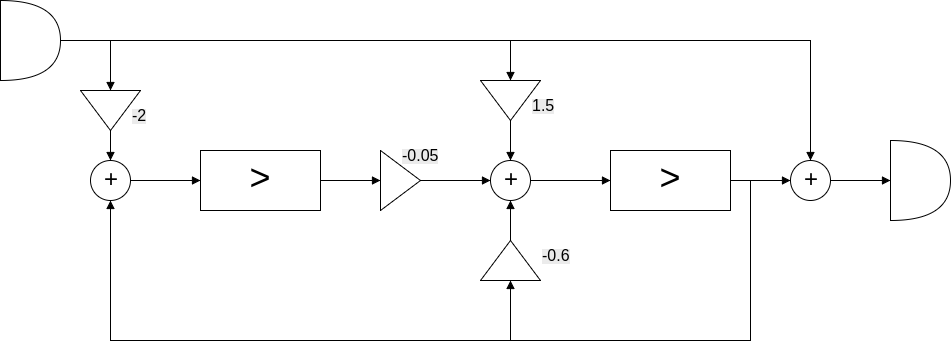
Számoljuk ki a rendszer impulzusválaszát!
A számolás módja az elődásjegyzetben van részletezve, ide csak a fontosabb rész-eredményeket vésem le.
A, B, C, D mátrixok
Saját értékek, Lagrange Mátrixok
Impulzusválasz
