„Algoritmuselmélet 2010.11.19. PZH megoldásai” változatai közötti eltérés
A VIK Wikiből
| 57. sor: | 57. sor: | ||
}} | }} | ||
===6. Feladat=== | ===6. Feladat (Van megoldás)=== | ||
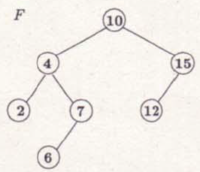
Hajtsa végre az alábbi <math>F</math> bináris keresőfán a BESZÚR(13), TÖRÖL(10) műveleteket! Minden lépést jelezzen! | |||
[[File:algel_pzh_2010osz_6_f.PNG|200px]] | |||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
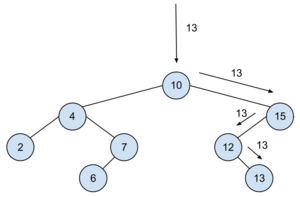
*BESZÚR(13): | |||
**Egyszerű, mint az 1x1<br> | |||
[[File:algel_pzh_2010osz_6_1.png|300px]] | |||
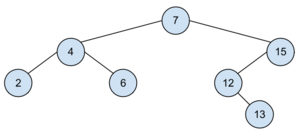
*TÖRÖL(10): | |||
**Töröljük a 10-t. | |||
**A '''BAL''' oldali részfából kiválasztjuk a '''LEGNAGYOBB''' elemet, és berakjuk a gyökérbe (ebben az esetben a 7). | |||
**A fát rendbe rakjuk (ez esetben a 6-t beírjuk a 7 régi helyére).<br> | |||
[[File:algel_pzh_2010osz_6_2.png|300px]] | |||
}} | }} | ||
A lap 2013. június 19., 20:47-kori változata
2010.11.19 - PZH megoldásai
1. Feladat
TODO
Megoldás
TODO
2. Feladat
TODO
Megoldás
TODO
3. Feladat
TODO
Megoldás
TODO
4. Feladat (Van megoldás)
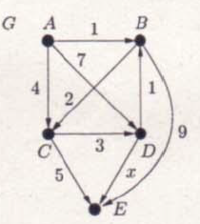
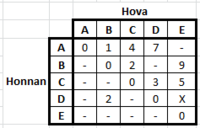
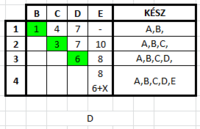
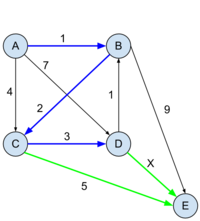
Dijkstra algoritmussal határozza meg a G gráfban az pontból az összes többi pontba menő legrövidebb utak hosszát az pozitív valós paraméter függvényében. Minden lépésnél írja fel a távolságokat tartalmazó D tömb állapotát, és a KÉSZ halmaz elemeit.
5. Feladat
TODO
Megoldás
TODO
6. Feladat (Van megoldás)
Hajtsa végre az alábbi bináris keresőfán a BESZÚR(13), TÖRÖL(10) műveleteket! Minden lépést jelezzen!
7. Feladat
TODO
Megoldás
TODO
8. Feladat
TODO
Megoldás
TODO