„Algoritmuselmélet 2010.11.19. PZH megoldásai” változatai közötti eltérés
A VIK Wikiből
Új oldal, tartalma: „{{Vissza|Algoritmuselmélet}} == 2010.11.19 - PZH megoldásai== ===1. Feladat=== TODO {{Rejtett |mutatott=<big>'''Megoldás'''</big> |szöveg= TODO }} ===2. Feladat=…” |
|||
| 32. sor: | 32. sor: | ||
===4. Feladat=== | ===4. Feladat=== | ||
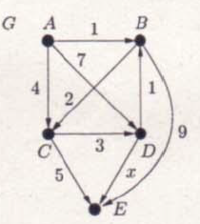
Dijkstra algoritmussal határozza meg a G gráfban az <math>A</math> pontból az összes többi pontba menő legrövidebb utak hosszát az <math>X</math> pozitív valós paraméter függvényében. Minden lépésnél írja fel a távolságokat tartalmazó D tömb állapotát, és a KÉSZ halmaz elemeit. | |||
[[File:algel_pzh_2010osz_4_f.PNG|200px]] | |||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
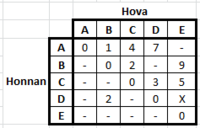
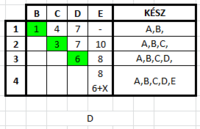
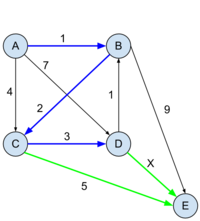
*Egy egyszerű Dijkstra-s feladat. | |||
*Annyit kell megjegyezni hozzá, hogy: | |||
**Ha <math> X \leq 2 </math>, akkor az <math>X</math> élt <math>( D \rightarrow E )</math> veszi be. | |||
**Ha <math> X \geq 2 </math>, akkor a <math>C \rightarrow E </math> élt veszi be. | |||
:::::::::[[File:algel_pzh_2010osz_4_2.PNG|200px]][[File:algel_pzh_2010osz_4_3.PNG|200px]][[File:algel_pzh_2010osz_4_1.png|200px]] | |||
}} | }} | ||
A lap 2013. június 19., 11:26-kori változata
2010.11.19 - PZH megoldásai
1. Feladat
TODO
Megoldás
TODO
2. Feladat
TODO
Megoldás
TODO
3. Feladat
TODO
Megoldás
TODO
4. Feladat
Dijkstra algoritmussal határozza meg a G gráfban az pontból az összes többi pontba menő legrövidebb utak hosszát az pozitív valós paraméter függvényében. Minden lépésnél írja fel a távolságokat tartalmazó D tömb állapotát, és a KÉSZ halmaz elemeit.
Megoldás
- Egy egyszerű Dijkstra-s feladat.
- Annyit kell megjegyezni hozzá, hogy:
- Ha , akkor az élt veszi be.
- Ha , akkor a élt veszi be.
5. Feladat
TODO
Megoldás
TODO
6. Feladat
TODO
Megoldás
TODO
7. Feladat
TODO
Megoldás
TODO
8. Feladat
TODO
Megoldás
TODO
