„Laboratórium 1 - 2. Mérés: Alapmérések” változatai közötti eltérés
Új oldal, tartalma: „{{GlobalTemplate|Villanyalap|LaborI2esMeres}} ==Ellenőrző kérdésekre a válaszok:== <ol> <li><b>Egy digitális feszültségmérő 2 V-os méréshatárában 0.050 …” |
aNincs szerkesztési összefoglaló |
||
| (10 közbenső módosítás, amit 7 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
{{ | {{Vissza|Laboratórium 1}} | ||
__TOC__ | |||
== | == A mérésről == | ||
< | == Házihoz segítség == | ||
== Beugró kérdések kidolgozása == | |||
'''''<span style="color: red">Ezt a részt még aktualizálni kell, meg valami pofásabb formára kéne hozni. Az első kérdéseknél megadtam az alapot, a többit is így kéne megformázni </span> - [https://wiki.sch.bme.hu/bin/view/Villanyalap/LaborI2esMeres Régi wikioldal]''''' | |||
'''1. Egy digitális feszültségmérő 2 V-os méréshatárában 0.050 V-ot mutat. Mekkora a kvantálásból származó hiba?''' | |||
Kvantálási hiba: digitális műszer utolsó számjegyének/digitjének hibája, százalékban a mért értékre vonatkoztatva. Itt: <math> \frac{{0,001}} {{0,050}} = 2\% </math> | |||
'''2. Egy Deprez-műszer segítségével soros Ohm-mérőt építünk. Mekkorára válasszuk az Rs soros ellenállást, ha a mérendő ellenállás névleges értéke R = 1 kOhm, és maximális mérési pontosságot szeretnénk elérni? Mekkora a mérés bizonytalansága abban az esetben, ha a műszer osztálypontossága 0.5%?''' | |||
soros ellenállást, ha a mérendő ellenállás névleges értéke R = 1 kOhm, és maximális | |||
mérési pontosságot szeretnénk elérni? Mekkora a mérés bizonytalansága abban az | |||
esetben, ha a műszer osztálypontossága 0.5%? | |||
o.p. Analóg műszer kitérésének hibája a maximális kitérésre vonatkoztatva, százalékban [angolul accuracy], esetleg % jel nélkül jelezve [angolul class] : <math> | |||
\frac{{h_{abs} }} | \frac{{h_{abs} }} | ||
{{x_{{\text{max}}} }} \cdot 100 | {{x_{{\text{max}}} }} \cdot 100 | ||
| 86. sor: | 85. sor: | ||
<b>Egy Deprez-rendszerű feszültségmérővel egyenfeszültséget mérünk. A műszer skálabeosztása lineáris, végkitérése 100 osztás, méréshatára 10 V, osztálypontossága | |||
1%. A műszer kitérése 65 osztás. Mekkora a mért feszültség értéke, és a mérés | 1%. A műszer kitérése 65 osztás. Mekkora a mért feszültség értéke, és a mérés | ||
bizonytalansága?</b> | bizonytalansága?</b> | ||
| 96. sor: | 95. sor: | ||
</math> | </math> | ||
<b>Rajzolja fel az általános Wheatstone-híd kapcsolását, és adja meg a kiegyenlítés | |||
feltételét!</b> | feltételét!</b> | ||
Egymással <u>átellenesen</u>: párhuzamos(soros(<math> R_1 </math>, <math> R_2 </math>),soros(<math> R_3 </math>, <math> R_4 </math>)). A híd kimeneti feszültségét a bemeneti feszültségből feszültségosztással kapjuk: <math> | Egymással <u>átellenesen</u>: párhuzamos(soros(<math> R_1 </math>, <math> R_2 </math>),soros(<math> R_3 </math>, <math> R_4 </math>)). A híd kimeneti feszültségét a bemeneti feszültségből feszültségosztással kapjuk: <math> | ||
| 104. sor: | 103. sor: | ||
</math>. Kiegyenlített a híd, ha <math> U_ki = 0 </math>, azaz <math> R_2 R_3 = R_1 R_4 </math>. | </math>. Kiegyenlített a híd, ha <math> U_ki = 0 </math>, azaz <math> R_2 R_3 = R_1 R_4 </math>. | ||
'''5. 1 V csúcsértékű 50 Hz frekvenciájú szimmetrikus háromszögjelet mérünk Deprezműszerrel. A méréshez aktív egyutas egyenirányítót használunk. A kapcsolásban használt ellenállások mindegyike R = 1 kOhm +/- 1%, a diódafeszültség Ud = 0.6 V a műszer végkitérése 1 V, és osztálypontossága 0.5%, a műveleti erősítő ideálisnak tekinthető.''' | |||
A méréshez aktív egyutas egyenirányítót használunk. A kapcsolásban | * '''Adja meg a kapcsolási rajzot, és a műszer által mért jelalakot!''' | ||
használt ellenállások mindegyike R = 1 kOhm +/- 1%, a diódafeszültség Ud = 0.6 V a | * '''Milyen értéket mutat a műszer?''' | ||
műszer végkitérése 1 V, és osztálypontossága 0.5%, a műveleti erősítő ideálisnak | * '''Adja meg mérés eredő bizonytalanságát, az összes hibakomponens "worst case" alapú összegzésével!''' | ||
tekinthető. | |||
alapú összegzésével! | |||
[[File:Labor1 Kép30.gif]] | |||
Valamelyik félhullám esetén valamelyik dióda nem vezet, tehát szakadásnak vehető, a másik dióda vezet, tehát egy 0,6V-os generátornak tekinthető. Ekkor felírható az ideális erősítő invertáló bemenetére a csomóponti áram: <math> | |||
\frac{{U_{be} }} | \frac{{U_{be} }} | ||
{{R_1 }} + \frac{{U_{ki1}}} | {{R_1 }} + \frac{{U_{ki1}}} | ||
| 160. sor: | 156. sor: | ||
<math> | <math> | ||
h = \pm (o.v. + o.r.\frac{{U_{ | h = \pm (o.v. + o.r.\frac{{U_{max} }} | ||
{{U_{ | {{U_{mert} }} + \frac{{0,001}} | ||
{{U_{mert} }} \cdot 100\% ) = \pm 0,074\% | {{U_{mert} }} \cdot 100\% ) = \pm 0,074\% | ||
</math> | </math> | ||
<li>Rajzolja fel a dual-slope átalakító blokkvázlatát és ismertesse a működését! Fejezze ki a | <li><b>Rajzolja fel a dual-slope átalakító blokkvázlatát és ismertesse a működését! Fejezze ki a | ||
mért feszültséget! | mért feszültséget!</b> | ||
Zoltán István: Méréstechnika 91-92 old. | |||
<li><b>10 V effektív értékű szabályos valamilyenjelet mérünk akármilyenérték-mérő AC voltmérővel. | <li><b>10 V effektív értékű szabályos valamilyenjelet mérünk akármilyenérték-mérő AC voltmérővel. | ||
| 180. sor: | 177. sor: | ||
Alább egy táblázat mutatja, hogy adott ''amplitudójú'' jel esetén az adott értéket mérő eszköz mit '''mér''' (nyílván az adott értéket), mit '''mutat''' (a hosszú mondat fent), és a mutatott értéket milyen *szorzó*val kell megszorozni, hogy a jel ''effektív értékét'' kapjam meg. | Alább egy táblázat mutatja, hogy adott ''amplitudójú'' jel esetén az adott értéket mérő eszköz mit '''mér''' (nyílván az adott értéket), mit '''mutat''' (a hosszú mondat fent), és a mutatott értéket milyen *szorzó*val kell megszorozni, hogy a jel ''effektív értékét'' kapjam meg. | ||
{| class="wikitable" border="1" | |||
| | |- | ||
! rowspan="2" | Jelalak !! colspan="3"| Effektív érték !! colspan="3"| Abszolút középérték !! colspan="3"| Csúcsérték | |||
| | |- | ||
| mér || mutat || szorzó || mér || mutat || szorzó || mér || mutat ||szorzó | |||
| | |- | ||
|Szinusz|| <math> \frac{1}{\sqrt{2}} </math> || <math> \frac{1}{\sqrt{2}} </math> || style="text-align: center;" | <math> 1 </math>||<math> \frac{2}{\pi} </math> || <math> \frac{1}{\sqrt{2}} </math>||<math> \frac{\pi}{2 \sqrt{2}} </math>|| style="text-align: center;" | <math> 1 </math>||<math> \frac{1}{\sqrt{2}} </math>||<math> \frac{1}{\sqrt{2}} </math> | |||
| | |- | ||
|Háromszög||<math> \frac{1}{\sqrt{3}} </math>||<math> \frac{1}{\sqrt{3}} </math>|| style="text-align: center;" | <math> 1 </math>||<math> \frac{1}{2} </math>||<math> \frac{\pi}{4 \sqrt{2}} </math>||<math> \frac{\pi}{2 \sqrt{2}} </math>|| style="text-align: center;" | <math> 1 </math>||<math> \frac{1}{\sqrt{2}} </math>||<math> \frac{1}{\sqrt{2}} </math> | |||
|- | |||
|Négyszög||style="text-align: center;" | <math> 1 </math>|| style="text-align: center;" | <math> 1 </math>|| style="text-align: center;" | <math> 1 </math>|| style="text-align: center;" | <math> 1 </math>||<math> \frac{\pi}{2 \sqrt{2}} </math>||<math> \frac{\pi}{2 \sqrt{2}} </math>|| style="text-align: center;" | <math> 1 </math>||<math> \frac{1}{\sqrt{2}} </math>||<math> \frac{1}{\sqrt{2}} </math> | |||
|} | |} | ||
| 281. sor: | 280. sor: | ||
DC feszültségmérés pontossága: +/- (0.05% o.v. + 0.005% o.r)</b> | DC feszültségmérés pontossága: +/- (0.05% o.v. + 0.005% o.r)</b> | ||
<li><b>Egy oszcilloszkóp bemenete 1 | <li><b>Egy oszcilloszkóp bemenete 1 MOhm ellenállással és a vele párhuzamosan kapcsolódó 30 pF értékű | ||
kapacitással modellezhető. A mérendő jelet egy 5 MOhm-os soros ellenálláson keresztül | kapacitással modellezhető. A mérendő jelet egy 5 MOhm-os soros ellenálláson keresztül | ||
vezetjük az oszcilloszkóp bemenetére. Mekkora kapacitású kondenzátort kell a soros | vezetjük az oszcilloszkóp bemenetére. Mekkora kapacitású kondenzátort kell a soros | ||
ellenállással párhuzamosan kapcsolni ahhoz, hogy a jel hozzávezetés frekvenciafüggetlen | ellenállással párhuzamosan kapcsolni ahhoz, hogy a jel hozzávezetés frekvenciafüggetlen | ||
legyen?</b> | legyen?</b> | ||
Akkor frekvenciafüggetlen ha a két párhuzamos kapcsolás időállandója egyenlő. Ez azt jelenti hogy Rs*C=Ro*Co. Ebből az egyenletből kifejezhető C. C=6pF. | |||
<li><b>Adott egy fojtótekercs, melynek 30 Ohm ellenállása és 400 Ohm a reaktanciája. 40 V, | <li><b>Adott egy fojtótekercs, melynek 30 Ohm ellenállása és 400 Ohm a reaktanciája. 40 V, | ||
50 Hz tápfeszültség esetén mekkora az áram abszolút értéke és fázisszöge? Mekkora az | 50 Hz tápfeszültség esetén mekkora az áram abszolút értéke és fázisszöge? Mekkora az | ||
| 294. sor: | 294. sor: | ||
<li><b>Rajzolja fel egy három voltmérős teljesítménymérés fazor ábráját!</b> | <li><b>Rajzolja fel egy három voltmérős teljesítménymérés fazor ábráját!</b> | ||
[[Kategória:Villamosmérnök]] | |||
A lap jelenlegi, 2020. szeptember 20., 17:45-kori változata
A mérésről
Házihoz segítség
Beugró kérdések kidolgozása
Ezt a részt még aktualizálni kell, meg valami pofásabb formára kéne hozni. Az első kérdéseknél megadtam az alapot, a többit is így kéne megformázni - Régi wikioldal
1. Egy digitális feszültségmérő 2 V-os méréshatárában 0.050 V-ot mutat. Mekkora a kvantálásból származó hiba?
Kvantálási hiba: digitális műszer utolsó számjegyének/digitjének hibája, százalékban a mért értékre vonatkoztatva. Itt:
2. Egy Deprez-műszer segítségével soros Ohm-mérőt építünk. Mekkorára válasszuk az Rs soros ellenállást, ha a mérendő ellenállás névleges értéke R = 1 kOhm, és maximális mérési pontosságot szeretnénk elérni? Mekkora a mérés bizonytalansága abban az esetben, ha a műszer osztálypontossága 0.5%?
o.p. Analóg műszer kitérésének hibája a maximális kitérésre vonatkoztatva, százalékban [angolul accuracy], esetleg % jel nélkül jelezve [angolul class] : Ebből relatív (a mért értékre vonatkoztatott) mérési hibát így kapunk:
Hogyan mérünk egy árammérővel, és egy soros ellenállással ellenállást ? Megmérjük először csak a soros ellenálláson átfolyó áramot: , majd megmérjük a mindkét ellenálláson átfolyó áramot: . A fenti egyenletekből: illetve amire még később szükség lesz: Majd ezek tudatában elkezdjük addig variálni az utóbbit, amíg benne nem lesz az osztálypontosság (ugyanis más mérési hibát nem ismerünk). R hibája az árammérés hibájára vonatkoztatva (Amper/Ohm a mértékegysége, de tök mindegy). . R relatív hibája :
Ennek kell a minimumát keresni szerint (for advanced users: az az érték, ahol az szerinti derivált nulla: )
Nevezővel beszorozhatunk sosem lesz nulla Ha akkor
Egy Deprez-rendszerű feszültségmérővel egyenfeszültséget mérünk. A műszer skálabeosztása lineáris, végkitérése 100 osztás, méréshatára 10 V, osztálypontossága
1%. A műszer kitérése 65 osztás. Mekkora a mért feszültség értéke, és a mérés
bizonytalansága?
6,5V-ot mértünk, és az osztálypontosság fenti definíciója alapján
Rajzolja fel az általános Wheatstone-híd kapcsolását, és adja meg a kiegyenlítés feltételét! Egymással átellenesen: párhuzamos(soros(, ),soros(, )). A híd kimeneti feszültségét a bemeneti feszültségből feszültségosztással kapjuk: . Kiegyenlített a híd, ha , azaz .
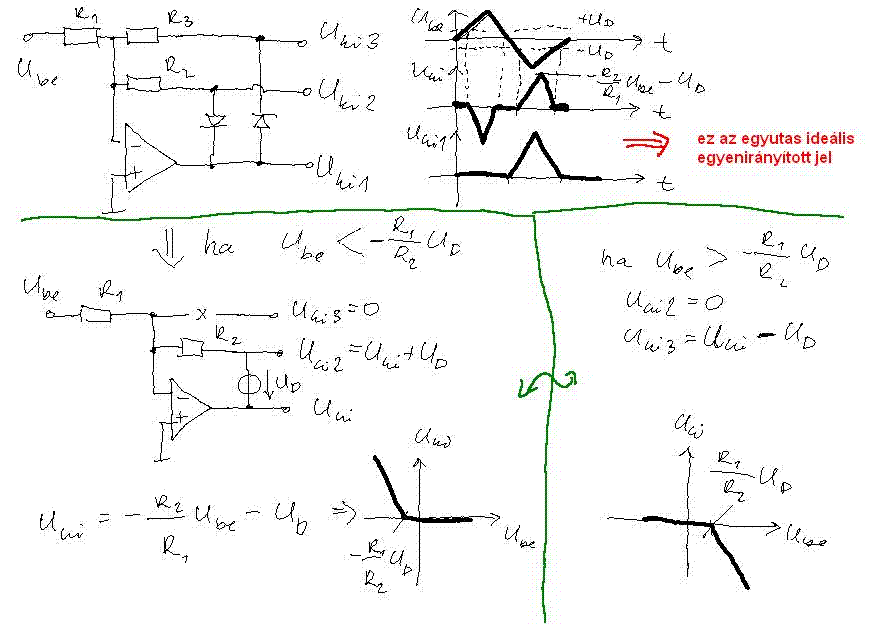
5. 1 V csúcsértékű 50 Hz frekvenciájú szimmetrikus háromszögjelet mérünk Deprezműszerrel. A méréshez aktív egyutas egyenirányítót használunk. A kapcsolásban használt ellenállások mindegyike R = 1 kOhm +/- 1%, a diódafeszültség Ud = 0.6 V a műszer végkitérése 1 V, és osztálypontossága 0.5%, a műveleti erősítő ideálisnak tekinthető.
- Adja meg a kapcsolási rajzot, és a műszer által mért jelalakot!
- Milyen értéket mutat a műszer?
- Adja meg mérés eredő bizonytalanságát, az összes hibakomponens "worst case" alapú összegzésével!
Valamelyik félhullám esetén valamelyik dióda nem vezet, tehát szakadásnak vehető, a másik dióda vezet, tehát egy 0,6V-os generátornak tekinthető. Ekkor felírható az ideális erősítő invertáló bemenetére a csomóponti áram: Látszik, hogy invertáló erősítő, és erősítése 1 lesz, ha az ellenállások megegyeznek.
A műszer absz. középértékét méri (integrálás, háromszögek területe..): -ot mutat a műszer.
Ehhez még hozzájön az osztálypontosságból adódó hiba:
Így a mérés bizonytalansága 6%.
| Jelalak | Effektív érték | Abszolút középérték | Csúcsérték | ||||||
|---|---|---|---|---|---|---|---|---|---|
| mér | mutat | szorzó | mér | mutat | szorzó | mér | mutat | szorzó | |
| Szinusz | |||||||||
| Háromszög | |||||||||
| Négyszög | |||||||||