„Számítógépes grafika és képfeldolgozás házi feladat kiírások” változatai közötti eltérés
autoedit v2: fájlhivatkozások egységesítése, az új közvetlenül az adott fájlra mutat |
|||
| (13 közbenső módosítás, amit 5 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
< | {{RightTOC}} | ||
{{Vissza|Grafika}} | |||
</ | |||
==2015/1 őszi félév== | |||
=== Első feladat === | |||
Adott egy 1000m x 1000m-res mező, amelyet kezdetben a teljes viewport-ban látunk. Az egér bal gomb lenyomásával pontokat helyezünk el a mezőn. A pontokat piros belsejű, fehér körvonalú 5m sugarú körrel jelenítjük meg. Egyrészt a pontok egy fehér, önmagában zárt Catmull-Rom spline kontrollpontjai, amelyekhez tartozó időparaméter a lenyomáskori óra állás. Másrészt az első két pont egy egyenest definiál, a harmadik pedig egy fókusz pontot. A egyenes és fókuszpont által kijelölt parabola a síkot két részre osztja. A parabola fókuszpontot tartalmazó részében a hátteret sárgára, a másik részben türkizre színezzük ki. A Catmull-Rom spline és a parabola egyik metszéspontjában (már ha van) zöld színnel érintő egyenest rajzolunk mind a parabolához, mind pedig a spline-hoz. | |||
A SPACE lenyomásának hatására a kamera ablak 500m x 500m-resre megy össze úgy, hogy a középpontja helyben marad. Ezután (2m/sec,3m/sec) kezdeti sebességgel vándorútra indul. Ha a kameraablak ütközik a mező szélével, onnan biliárd golyó módjára verődik vissza. | |||
Minden, a feladat szövege által nem specifikált részlet szabadon megválasztható. | |||
=== Második feladat === | |||
Készítsen sugárkövető programot, amely egy szobát és az abban mozgó üveg ellipszoidot jelenít meg mozgó pontszerű fényforrás megvilágítása mellett. | |||
<b>A virtuális világban a fény terjedési sebessége 1 m/s!!! (ezen feltételt mellőző megoldások nem fogadhatók el)</b> | |||
A szoba egyik oldala aranyból van, optikailag sima és forgásparaboloid geometriájú. A szoba többi oldala diffúz és valamilyen mintával textúrázott sík. A szoba mérete 10 m x 10 m x 10 m volna, ha eltekintenénk a paraboloid kitüremkedésétől. | |||
Az üveg ellipszoid tengelyei a világkoordinátarendszer egyik tengelyével sem párhuzamosak. A leghosszabb tengely 2 m, a legrövidebb 0.5 m. Az ellipszoid egyenes vonalú egyenletes mozgást véget a szoba sarkából 0.5 m/sec sebességgel úgy, hogy legalább 10 másodpercig a szoba belsejében tartózkodik, mialatt a kamerából látható. | |||
A pont fényforrás ugyancsak egyenesvonalú egyenletes mozgást végez úgy, hogy az első 10 másodpercben a szoba beljesében van. | |||
A programnak a SPACE lenyomásának időpontjában keletkezett képet kell megjelenítenie. | |||
Az arany törésmutatója és kioltási tényezője: r: 0.17/3.1, g: 0.35/2.7, b: 1.5/1.9 | |||
Az üveg törésmutatója és kioltási tényezője: r: 1.5/0, g: 1.5/0, b: 1.5/0 | |||
=== Harmadik feladat === | |||
Készítsen CSIRGURU BOMBÁZÓ játékot. A csirguru a csirke és a kenguru nászából született jószág, csirke teste, csőre, szemei, taraja van, valamint egy lába, amivel kenguruszerűen ugrál. A lába a csípőízületben nem fordul el, a térízületben hátra fordul, a bokában előre (amit a normál csirke esetében hajlamosak vagyunk előre hajló térdnek hinni). Az egy szem lábujj ugyancsak felfelé hajlítható, az ízületek tengelyei egymással párhuzamosak. | |||
A csirguruk testét néhány zárt Bézier görbével definiált keresztmetszetek Catmull-Rom spline-t alkalmazó transzfinit interpolációjával kell létrehozni. A szem, csör, taraj, lábrészek ismert egyenletű paraméteres felületekből (pl. gömb, kúp, henger, paraboloid stb.) összerakhatók. | |||
A csirguruk egy sík, textúrázott és megvilágított terepen a bomba aktuális helye alatt, a program indításától számított másodpercenként születnek meg, majd elkezdenek ugrándozni. A lendületvételi fázisban a csirguru feneke a földhöz közelít, majd a térdízület EGYENES VONALÚ GYORSULÓ MOZGÁST (inverz kinematika) végez, mialatt a lábujj a talajon marad, a térd pedig vízszintesen tartja a csirgurut. A bokaízület kiegyenesedése pillantában a csirguru elszakad a földtől és lendületvétel végén elért kezdősebességű ferde hajítással leírható pályán ugrik, a levegőben előreteszi a lábát, a földetérkezésnél pedig a lendületvételt visszafelé játsza le. Az ugrálást ismételgetheti, az egyes ugrálások között a haladási irányát ízlésesen változtatva. | |||
A felhasználó egy bombát irányíthat a mező fölött egy síkban az A, W, D, Y billentyűkkel, majd SPACE-re a bomba leesik. Ha a bomba egy csirguru közelében esik le, a csirguru testrészei független ferde hajítást követnek, mialatt midegyik testrész egy-egy forgástengely körül forog. | |||
A színteret egy irányfényforrás (nap) és ambiens fényforrás világítja meg, a csirguruk és a bombák a talajra árnyékot (síkra vetített árnyék algoritmus) vetnek. | |||
==2014/15 tavaszi félév== | |||
=== Első feladat === | |||
Készítsen elől-felül-oldalnézetes ortografikus 3D Renner spline görbeszerkesztőt, amelyben a pálya menti sebesség közelítőleg 1 m/sec. A 600x600 pixel felbontású alkalmazói ablak négy egyenlő részre van osztva, amelyekben az elől, felül és oldalnézetek látható, egy negyed pedig üres. A világ 3m x 3m x 3m-res kocka, amelynek középpontjában vettük fel az origót. A nézetekben a teljes világ vetületei látszanak, az origó értelemszerűen középen van. A transzformációkat „kézzel” kell számítani, az OpenGL mátrixok most még nem alkalmazhatók. | |||
Amíg még nincs görbénk, az egyik nézetbeli egérkattintások kontrolpontokat vesznek fel, úgy, hogy a nézetre merőleges koordináta zérus. A további nézetekbe kattintva az ott legközelebbinek talált kontrollpont áthelyezhető, a nézetre merőleges koordináta változatlanul hagyásával. A pillanatnyi állapotot minden nézetben jelezni kell, a kontrolpontokat sárga körökkel, a 3D Renner spline-t pedig a fehéren rajzolt 2D merőleges vetületeivel. | |||
A SPACE lenyomására egy kör indul el a görbe kezdőpontjából és a sebességvektorát farokként maga után húzva, kb. 1 m/sec pályamenti sebességgel végigcsúszik a görbén. | |||
=== Második feladat === | |||
Készítsen sugárkövető programot, amely 100 mm oldalhosszúságú, egyik oldalán nyitott dobozban lévő durván tesszellált, optikailag sima, tükröző arany tóruszt, és egy Schwarzschild típusú (azaz töltés nélküli és nem forgó) Föld tömegű fekete lyukat tartalmaz. A doboz oldalai diffúz+spekuláris visszaverődésűek, a diffúz tag procedúrálisan textúrázott. A színteret ambiensfény és legalább egy pontfényforrás világítja meg. Élhet azzal az egyszerűsítéssel, hogy a fekete lyuk a fényt csak az első visszaverődés után görbíti, azaz a pont fényforrás és a megvilágított felület között nem, de a rücskös és sima felületek között, valamint a felületek és a szem között igen (a másik alternatíva a fényforrásból kilépő fény görbítésére a fotontérkép módszer). A fény elgörbülését kellő tudásszomj esetén Einstein téregyenletének Schwarzschildtól származó megoldásával, egyébként pedig az ekvivalenciaelv és a klasszikus newtoni gravitációs formula felhasználásával, sugármasírozással kell szimulálni. A rendelkezésre álló CPU idő 120 sec, szükség esetén kisebb bontású kép átmintavételezésével, távolságtól függő lépés-nagysággal és befoglaló térfogatokkal lehet a programot gyorsítani. | |||
A szükséges fizikai állandók: A fény sebessége: 300 000 km/sec; A föld kerülete: 40 000 km; A nehézségi gyorsulás a föld felszínén: 10 m/sec^2. | |||
Az arany törésmutatója és kioltási tényezője: r: 0.17/3.1, g: 0.35/2.7, b: 1.5/1.9 A falak diffúz és spekuláris visszaverődési tényezője és shininess paramétere, valamint a textúra szabadon megválasztható. | |||
=== Harmadik feladat === | |||
Készítsen pingvin (Pygoscelis antarcticus) szimulátort. A pingvin teste a Geometriai modellezés diasor 25. diáján szereplő felosztási séma szerinti Catmull-Clark felosztott felület, amit négyszög hálóból minimum egy, de a teljes megoldáshoz legalább két lépéssel kell felosztani. A teljes megoldásban a 40. dián lévő half-edge adatstruktúrában kell a geometriát tárolni. A pingvin teste texúrázott, diffúz, a textúrakoordinátákat hengerkoordinátákból kell számítani (hengeres vetítés). A textúra maga procedurális. A pingvinnnek még két szeme van, csőre és két mozgatható merev vagy több ízületből összerakott lába van, amit felosztott felülettel vagy paraméteres felületekből kell kialakítani. | |||
A havas terepen diffúz/spekuláris tojások vannak. Az avatár pinvginünket W=jobbra fordul, E=előre lép, R=balra fordul, SPACE=leül billentyűkkel lehet irányítani. Ha a pingvin 3 másodpercet ül egy tojáson, akkor a tojás kikel és egy újabb pingvin születik azon a helyen, amely őseihez hasonlóan rohan tojásokat kikelteni. A kamera az avatár pingvinre néz mindig, de poziciója állandó. A nap, lévén, hogy a Déli sarok közelébe vagyunk, lapos szögbe világítja meg a sík tájat, tojásokat és pingvineket. A síkon, síkra vetített árnyékok láthatók, amelyek feketék. | |||
==2014/15 őszi félév== | |||
=== Első feladat === | |||
[[File:Graf_2014-15_01.png|thumb|300px|2014 ősz, 1. hf]] | |||
Készítsen „Síkon táncoló kontrollpontok” programot. A felhasználó az egér balgomb egyszeri lenyomással/elengedéssel veszi fel a kontrollpontokat (max 10-et), amelyekhez 2cm sugarú kisebb fekete köröket rendelünk. Ha a kontrollpontok száma legalább kettő, azokra egy türkiszkék színű, kitöltött konvex burkot, piros Bézier görbét, nulla kezdő és végsebességű, a kontrollpont lehelyezésének idejét paraméterként használó zöld Catmull-Rom spline-t és kék Catmull-Clark görbét illeszt. | |||
A háttér világosszürke. Legnagyobb prioritása a kontrollpontoknak van, majd a görbék jönnek, végül jön a konvex burok. | |||
Space lenyomására a kontrollpontok egy-egy 5 cm-es kör tetejéről elindulva, 5 másodpercenként egy teljes fordulatot téve, elkezdenek keringeni, mégpedig a páros indexűek az óramutató járásával megegyező, a páratlan indexűek pedig azzal ellentétes irányban. A konvex burok és a görbék követik a kontrollpontokat. Mindezt a felhasználó egy 58cm x 68 cm-es kameraablakon keresztül látja. Ha a felhasználó az egér jobb gombbal rábök egy kontrollpontra, akkor a kameraablakot ehhez köti, a kontrollpont elmozdulása automatikusan a kameraablakot is arrébb viszi. | |||
=== Második feladat === | |||
Készítsen csendéletet, ahol procedurálisan textúrázott, diffúz+Blinn spekuláris asztalon optikailag sima tárgyak, egy ellipszoid aranykaktusz, egy paraboloid ezüstkaktusz és egy henger üvegkaktusz áll (a háromból min. kettő megvalósítása szükséges). A kaktuszoktörzséből a törzzsel hasonló, de kisebb részek nőnek ki, mindig a felületre merőlegesen, legalább két további szinten (az összes részek számát úgy kell megválasztani, hogy a program 1 percen belül lefusson). A kinövő részek véletlenszerűen, nagyjából egyenletesen oszlanak el a felületen. A teret egy zöldes, egy kékes, és egy pirosas pontfényforrás világítja meg, a megvilágítási intenzitás a távolság négyzetével csökken. Az égbolt világoskék. Árnyékok vannak. A kamera az asztal fölött van és enyhén lefelé néz. | |||
A sugár-objektum metszéspontot és a normálvektort a metszéspontban analitikusan kell számolni. | |||
Az említett anyagok törésmutatója (n) és kioltási tényezője (k): | |||
...................r..........g..........b | |||
Üveg (n/k)......1.5/0.0, 1.5/0.0, 1.5/0.0 | |||
Arany (n/k).....0.17/3.1, 0.35/2.7, 1.5/1.9 | |||
Ezüst (n/k).....0.14/4.1, 0.16/2.3, 0.13/3.1 | |||
=== Harmadik feladat === | |||
[[File:Graf_2014-15_03.png|thumb|300px|2014 ősz, 3. hf]] | |||
Készítsen szimulátort műhold befogáshoz a Мир űrállomás számára! A fényforrás a távoli nap. Az űrállomás a csillagos égbolt előtt, egy diffúz, procedurálisan textúrázott bolygó körül kering, pályája nem geostracionárius. A bolygót átlátszó kékes légkör veszi körül. Az űrállomás teste fémes csillogású forgástest, a sziluett Catmull-Rom spline-nal adandó meg. Az űrállomáson van egy nagyjából kör alakú lyuk. Az űrállomáshoz legalább két napelem tábla tartozik. Az űrállomás egy, a fő tehetetlenségi iránytól különböző tengely körül lassan forog. | |||
Az avatárunk éppen űrsétát végez, magát az űrállomáshoz kötve egy hosszú gumikötél végén rángatózva. A gumikötél csak egy adott távolság után feszül meg, azon túl Hooke törvény szerint nyúlik. Az űrállomástól nem zérus sebességgel rúgtuk el magunkat. Avatárunk tömege az űrállomás tömegénél sokkal kisebb. Az avatár mindig az űrállomás nyílása felé néz. | |||
A mesterséges hold gömb alakú, amiből legalább három henger vagy kúp alakú fúvóka nyúlik ki (bónusz: ha a fúvókák tengelye nem megy át a súlyponton, akkor a forgását is szabályozhatjuk). Kezdetben a műhold az űrállomáshoz képest lassan halad és forog. A műhold ugyancsak diffúz-spekuláris, a fúvókák színe alapján vezérelhetjük őket. Ha a q, w, ... billentyűket lenyomjuk, a betűhöz rendelt fúvókán egy lángnyelv tör ki, a műhold pedig ellentétes irányú I impulzust kap. A lendület és perdület, mint mindig, itt is megmarad. | |||
A játék célja, hogy a mesterséges hold az űrállomás nyílásán besétáljon. | |||
A harmadik feladat a játék "csendélete", még nem kell az objektumokat animálni és lángnyelvet sem kell kilőni. A virtuális világ életre keltése és vezérlése a negyedik házi feladata lesz. | |||
=== Negyedik feladat === | |||
Egészítse ki a 3. feladatot az ott specifikált felhasználói beavatkozási lehetőségekkel és animációval. | |||
==2013/14 őszi félév== | |||
=== Első feladat === | |||
[[File:Grafika_13osz_hazi1.png|thumb|300px|2013 ősz, 1. hf]] | |||
Készítsen "Kaksiulotteisia vihaisia lintuja" programot, amelyben egy piros és egy zöld madár szerepel, valamint világos zöld talaj, a talajból kiálló tetszőleges színű kétágú csúzli, amely fekete színű széles gumival fogja körbe a kilövendő piros madarat. A csúzli tára, ahol a piros madár várja a sorsa beteljesülését, a 600x600 felbontású alkalmazói ablak bal felső sarkához képest 200 pixellel jobbra és 400 pixellel lejjebb van. | |||
A madarak teste, szeme és szemgolyója ellipszis (nem kör!), csőrük, farktollaik és szemöldökeik háromszögek. Szárny és bóbita opcionális. A zöld madár fel-le repked akár szárnyak nélkül is, magassága az időben szinuszosan változik az ütközésig. A piros madarat csúzliból lehet kilőni a fizikai törvényeknek megfelelően, a csúzli rugóenergiáját teljes mértékben átveszi a madár induláskor. A kilövés folyamat azzal kezdődik, hogy az egér bal gombjának lenyomásával a madár ellipszis alakú testének belsejébe klikkelünk, amikor a madár a kurzorhoz ragad és követi az kurzor mozgását az egérgomb elengedéséig. A csúzli gumija végig szorosan feszül a madár fenekére. Amikor elengedjük a bal gombot a piros madarat is útjára bocsátjuk, azaz kirepül a csúzliból. Perdülettel és forgással nem kell foglalkozni. A piros madárra reptében a nehézségi erő hat, közegellenállás és felhajtóerő (nincs szárnya, amivel csapkodna) pedig nincs. Ha a piros és a zöld madár ellipszis teste ütközik (figyelem, két ellipszis ütközését pontosan kell számítani), mindketten megállnak a levegőben és a piros madár sárgává változik. Ha a piros madár kirepül a látható tartományból, automatikusan születik egy új a csúzliban fejjel lefelé a két ág "között". | |||
A feladat megoldásához csak az előadáson eddig szerepelt OpenGL függvények használhatók, azaz: glBegin, glEnd, glColor, glVertex, glViewport. | |||
Figyelem: a keret változott, ezért a korábbi évek kereteit nem lehet használni. | |||
Beadási határidő: 2013. 10. 01. 23:59 (Kiadás dátuma: 2013.09.18.) | |||
=== Második feladat === | |||
[[File:Grafika_13osz_hazi2.png|thumb|300px|2013 ősz, 2. hf]] | |||
Készítsen 2D editort, amivel egy 100m x 100m-es területet lehet berendezni, amelybe egy 50m x 50m-es ablakú kamerával nézünk bele. Az ablakot minden ‘s’ lenyomásra a (10, 20) vektor tolja el. Ha az ablak elérte a terület szélét, akkor visszaugrik a bal alsó sarokba. A program a bal egérgomb lenyomásainak helyét kontrollpontnak, az lenyomás pillanatában az óra állását pedig csomóértéknek (kontrollponthoz rendelt paraméterértéknek) tekinti, így minden bal egérgomb lenyomással egy újabb kontrollpontot vehetünk fel (max 10 kontrollpontra kell a programot felkészíteni). A kontrollpontokra egy fehér Tenziós Catmull-Rom (TCR) spline-t illeszt, ahol a tenzió mindenhol -0.5. A kontrollpontok nyugalmi állapotukban 1m sugarú piros kitöltött körök. | |||
Space lenyomására a program aktivizálódik, a spline-t megduplázza és az új változatot 60 fokkal a kontrollpontok súlypontja (aminek koordinátáit a kontrollpontok koordinátánkénti aritmetikai közepeként számíthatunk) körül elforgatja, majd kék Bézier görbét csinál belőle (mialatt az eredeti TCR marad a helyén). Ezután egy-egy 1 m sugarú sárga kitöltött kör indul el minden görbén, mégpedig a TCR-n a paraméterezésnek megfelelő időzítéssel, azaz annyi idő alatt ér a görbe végére, ameddig a kontrollpontot felvétele tartott. A Bézier-t a saját köre úgy futja be, hogy ugyanakkor érkezzen a végére, mint a TCR-n szaladó társa. A futamok újra kezdődnek. A futás alatt a kontrollpontokat ábrázoló kitöltött körök sugara folyamatosan változik amivel azt mutatják, hogy milyennek kell lennie az ide elhelyezett súly abszolút értékének, hogy a görbe aktuális pontját a kontrollpontok ilyen súlyokkal vett kombinációjaként kapjuk meg (Bézier-nél nyilván a Berstein polinom, TCR-nél érdemes gondolkodni egy kicsit). Ha a súly pozitív, a kör piros. Ha negatív, akkor türkisz kék. | |||
Figyelem: csak közelítőleg C2 folytonos és egzaktul C1 folytonos valódi, nem egyenletes TCR spline elfogadható, pl. Catmull-Rom és felesleges dolgokat tartalmazó Kochanek-Bartels nem. Közérthetőbben: az Internetről másolt spline-ok ellenjavaltak. | |||
Beadási határidő: 2013. 10. 20. 23:59 (Kiadás dátuma: 2013.10.04.) | |||
=== Harmadik feladat === | |||
[[File:Grafika_13osz_hazi3.png|thumb|300px|2013 ősz, 3. hf]] | |||
Készítsen négyhengeres sugárkövető programot. Az 1. henger tartalmazza a teljes színteret, fala optikailag sima arany, alapja megválasztható színű diffúz, teteje hiányzik, amin a fehér égbolt világít be (ezt úgy lehet figyelembe venni, hogy azok a sugarak, amelyek kilépnek a hengerből ilyen sugársűrűséggel térnek vissza). A többi henger az 1. belsejében van, tengelyük sem egymással, sem bármelyik koordinátatengellyel nem párhuzamos. A 2. anyaga optikailag sima ezüst, a 3. anyaga optikailag sima réz, a 4. anyaga optikailag sima üveg, gyémánt vagy megválasztható színű diffúz lehet. Az homogén égbolton kívül még egy vagy több optikailag sima ezüst forgásparaboloid reflektorú, nem a fókuszba helyezett pontszerű fényforrás világítja meg a teret. | |||
A kamerát úgy kell elhelyezni, hogy a hengerek láthatók legyenek. Fotontérképet nyilván csak a diffúz felületekhez kell rendelni az optikailag sima felületekhez nem. A fotonok számát úgy kell beállítani, hogy a program 1 percen belül 1 CPU magon lefusson (ha ezt az időt túllépi, a fotonszámot érdemes csökkenteni, pl. úgy, hogy ne legyen 10^4-nél lényegesen nagyobb, de a nem lépi túl, akkor lehet több fotonnal is dolgozni). A fotontérkép felbontását pedig úgy kell meghatározni, hogy a kausztika az adott fotonszám mellett sima legyen. | |||
Anyagtulajdonságok: | |||
Optikailag sima anyagok: | |||
<code> | |||
<pre> | |||
...................r..........g..........b | |||
Üveg (n/k)......1.5/0.0, 1.5/0.0, 1.5/0.0 | |||
Gyémánt (n/k)...2.4/0.0, 2.4/0.0 2.4/0.0 | |||
Arany (n/k).....0.17/3.1, 0.35/2.7, 1.5/1.9 | |||
Réz (n/k).......0.2/3.6, 1.1/2.6, 1.2/2.3 | |||
Ezüst (n/k).....0.14/4.1, 0.16/2.3, 0.13/3.1 | |||
</pre> | |||
</code> | |||
Diffúz anyagok: kd(r,g,b) tetszőlegesen, jó ízléssel megválasztható. | |||
Beadási határidő: 2013. 11. 10. 23:59 (Kiadás dátuma: 2013.10.25.) | |||
=== Negyedik feladat === | |||
[[File:Grafika_13osz_hazi4.png|thumb|300px|2013 ősz, 4. hf]] | |||
Készítsen OpenGL programot, amely egy (fekete foltos textúrájú), de alapvetően fehér diffúz+spekuláris testű Szalámi Gólyát és zöld diffúz+erősen spekuláris testű (nyálkás) Ellipszoid Békákat jelenít meg diffúz, textúrázott terepen. A Szalámi Gólya onnan ismerszik meg, hogy ha testét a Catmull-Rom spline vázára merőlegesen bárhol kettészeljük, akkor a metszet kör alakú (a váz definíciója: ha a Szalámi Gólya testének minden felületi pontját egyszerre gyújtjuk meg, akkor a tűzfrontok a vázban találkoznak). A kör sugara a váz mentén változik, amelyet egy másik Catmull-Rom spline-nal kell megadni. A gólyának és a békáknak is két-két szemük van, a gólyának még piros kúp alakú csőre és két gólyalába van (amelyek biológiai ismereteink szerint, a mi lábunkkal ellentétben, térdben előre és nem visszafelé hajlíthatók). A gólya arányai olyanok, hogy előrehajolva a csőrének végével elérné a talajt. Az Ellipszoid Békák testrészei ellipszoidok. A terep textúrázott, nem szükségképpen sík. Tereptárgyak tetszés szerint megválaszthatók. A színteret a nap (irányfényforrás) az ég (ambiens fényforrás) és egy energiától duzzadó szentjános bogár (pontfényforrás) világítja meg. | |||
Beadási határidő: 2013. 12. 04. 23:59 (Kiadás dátuma: 2013.11.20., Beadási határidő először: 2013. 12. 01. 23:59, majd kitolva a határidő: 2013.12.03.; UTÁNA szerverprobléma miatt: 2013.12.04. 23:59) | |||
=== Ötödik feladat === | |||
[[File:Grafika_13osz_hazi5.png|thumb|300px|2013 ősz, 5. hf]] | |||
Mozgassa meg a 4. házi objektumait. A gólya lépeget előre 1 lépés/sec sebességgel. A támaszkodó láb nem csúszkál (inverz kinematika). A ‘J’ billentyű lenyomására 0.5 sec alatt 10 fokot jobbra fordul célszerűen a támaszkodó láb körül, hasonlóan a ‘B’ billentyű lenyomására balra. A SPACE hatására a nyakát előrehajtva lecsap és ha békatestet talál (végtagok nem számítanak), akkor a béka eltűnik. A gólyát csontváz animációval kell mozgatni, a lábrészek és a nyak hossza nem változhat a mozgás során. A láb részei tekinthetők merev testnek, de a gólyatest nem, így azt a csontvázra "bőrözni" kell. A békák merev testként akár véletlen irányokba ugrálhatnak, de két ugrás között 1 sec rákészülési időre van szükségük. A terepet illetően két lehetőség közül lehet választani. Az elsőben a terep sík és akkor a testeknek van árnyékuk rajta, amit a nap vet (síkra vetített árnyék algoritmus). A másik lehetőség, hogy a terep nem sík. | |||
Beadási határidő: 2013. 12. 16. 11:00 (Kiadás dátuma: 2013.12.04.) | |||
==2012/13 tavaszi félév== | ==2012/13 tavaszi félév== | ||
=== Első feladat === | === Első feladat === | ||
[[ | [[File:Grafika_2013t_hf1.png|thumb|300px|2013 tavasz, 1. hf]] | ||
Készítsen breakout játékot, fejet hajtva a játékfejlesztés úttörői előtt. | Készítsen breakout játékot, fejet hajtva a játékfejlesztés úttörői előtt. | ||
| 23. sor: | 192. sor: | ||
=== Második feladat === | === Második feladat === | ||
[[ | [[File:Grafika_2013t_hf2.png|thumb|300px|2013 tavasz, 2. hf]] | ||
Készítsen 2D editort, ami az egér balgomb lenyomásokat kontrolpontokként értelmezi, amelyekre egy piros Catmull-Rom (CR) spline-t és egy zöld CRI-spline-t is illeszt. | Készítsen 2D editort, ami az egér balgomb lenyomásokat kontrolpontokként értelmezi, amelyekre egy piros Catmull-Rom (CR) spline-t és egy zöld CRI-spline-t is illeszt. | ||
| 103. sor: | 272. sor: | ||
===Első feladat=== | ===Első feladat=== | ||
[[ | [[File:Grafika_2011ő_hf1.png|thumb|300px|2011 ősz, 1. hf]] | ||
Készítsen 2D giliszta üldözéses játékot OpenGL-ben. | Készítsen 2D giliszta üldözéses játékot OpenGL-ben. | ||
| 118. sor: | 287. sor: | ||
===Második feladat=== | ===Második feladat=== | ||
[[ | [[File:Grafika_2011ő_hf2.png|thumb|300px|2011 ősz, 2. hf]] | ||
Készítsen üde zöld füves versenypályát kb. 4 cm-es 2.5 dimenziós atlétacsigák (Gastropoda Athleta Dimensio II.V) számára! Az atlétacsiga az éticsigával ellentétben bedől a kanyarban, lassításkor előre, fékezéskor hátra hajol, általában a rá ható erő irányába és azzal arányosan dönti a testét. Az atlétacsiga 2.5 dimenziós volta annyit jelent, hogy ugyan 2 dimenziós görbék által kitöltött területekből áll, de a görbék kontrolpontjainak van z koordinátája is, amely alapján a pont elmozdul az x,y síkon az erővel és a z koordinátával arányosan. A test határa zárt Catmull-Rom spline (amiből a vektorizáció konkáv sokszöget hoz létre, melyet fülvágó algoritmussal kell háromszögekre bontani), a szemek határai zárt Bézier görbék, a ház több Catmull-Clark subdivision görbével határolt sokszög. Az atlétacsiga referenciapontja (pivot pont) a referenciahelyzetében az origó, hossztengelye az y tengely (a referenciapont kerül mindig a pálya fölé, és e körül fordul el az atlétacsiga a haladási irányba). A csigát - a saját érdekében – a kontrolpontokon végrehajtott saját skálázással és elforgatással, majd a csúcspontokon glTranslatef függvényekkel kell pályára helyezni. A pálya ugyancsak zárt Catmull-Rom spline, hossza kb. 1 méter, a vezérlőpontokat POINT primitívekkel lehet felrajzolni. A virtuális világban az egységet cm-re kell választani. Az atlétacsiga a pályagörbe paraméterét egyenletesen változtatva mozog a pályán, 5 másodperc alatt ér körbe. Az egér bal gombjának lenyomása a pálya kurzorhoz legközelebbi kontrolpontját a kurzor aktuális helyére mozdítja. A kamera induláskor az egész pályát befogja, a z betű lenyomásával viszont rázoomol a csigára és követi a pályáján. A kamerát a gluOrtho2D függvénnyel kell implementálni. A Catmull-Rom és Catmull-Clark kötelező műsorszám. A fülvágás, Bézier görbe, interaktív pályamódosítás és zoom részfeladatokból mind megpróbálandó, de ezekből kettő lehet hibás is, attól még elfogadjuk a feladatot. | Készítsen üde zöld füves versenypályát kb. 4 cm-es 2.5 dimenziós atlétacsigák (Gastropoda Athleta Dimensio II.V) számára! Az atlétacsiga az éticsigával ellentétben bedől a kanyarban, lassításkor előre, fékezéskor hátra hajol, általában a rá ható erő irányába és azzal arányosan dönti a testét. Az atlétacsiga 2.5 dimenziós volta annyit jelent, hogy ugyan 2 dimenziós görbék által kitöltött területekből áll, de a görbék kontrolpontjainak van z koordinátája is, amely alapján a pont elmozdul az x,y síkon az erővel és a z koordinátával arányosan. A test határa zárt Catmull-Rom spline (amiből a vektorizáció konkáv sokszöget hoz létre, melyet fülvágó algoritmussal kell háromszögekre bontani), a szemek határai zárt Bézier görbék, a ház több Catmull-Clark subdivision görbével határolt sokszög. Az atlétacsiga referenciapontja (pivot pont) a referenciahelyzetében az origó, hossztengelye az y tengely (a referenciapont kerül mindig a pálya fölé, és e körül fordul el az atlétacsiga a haladási irányba). A csigát - a saját érdekében – a kontrolpontokon végrehajtott saját skálázással és elforgatással, majd a csúcspontokon glTranslatef függvényekkel kell pályára helyezni. A pálya ugyancsak zárt Catmull-Rom spline, hossza kb. 1 méter, a vezérlőpontokat POINT primitívekkel lehet felrajzolni. A virtuális világban az egységet cm-re kell választani. Az atlétacsiga a pályagörbe paraméterét egyenletesen változtatva mozog a pályán, 5 másodperc alatt ér körbe. Az egér bal gombjának lenyomása a pálya kurzorhoz legközelebbi kontrolpontját a kurzor aktuális helyére mozdítja. A kamera induláskor az egész pályát befogja, a z betű lenyomásával viszont rázoomol a csigára és követi a pályáján. A kamerát a gluOrtho2D függvénnyel kell implementálni. A Catmull-Rom és Catmull-Clark kötelező műsorszám. A fülvágás, Bézier görbe, interaktív pályamódosítás és zoom részfeladatokból mind megpróbálandó, de ezekből kettő lehet hibás is, attól még elfogadjuk a feladatot. | ||
| 187. sor: | 356. sor: | ||
===Első feladat=== | ===Első feladat=== | ||
[[ | [[File:Grafika_2011t_hf1.png|thumb|300px|2011 tavasz, 1. hf]] | ||
Egér labirintusban. | Egér labirintusban. | ||
| 199. sor: | 368. sor: | ||
===Második feladat=== | ===Második feladat=== | ||
[[ | [[File:Grafika_2011t_hf2.png|thumb|300px|2011 tavasz, 2. hf]] | ||
Készítsen Valentin napi dobogó szívecskét! | Készítsen Valentin napi dobogó szívecskét! | ||
| 211. sor: | 380. sor: | ||
===Harmadik feladat=== | ===Harmadik feladat=== | ||
[[ | [[File:Grafika_2011t_hf3.png|thumb|300px|2011 tavasz, 3. hf]] | ||
Üveg ellipszoid és rézből készült tesszellált, paraméteres felület arany falú csonkakúpban, sugárkövetéssel megjelenítve. | Üveg ellipszoid és rézből készült tesszellált, paraméteres felület arany falú csonkakúpban, sugárkövetéssel megjelenítve. | ||
| 255. sor: | 424. sor: | ||
===Első feladat=== | ===Első feladat=== | ||
[[ | [[File:Grafika_2010ő_hf1.jpg|thumb|300px|2010 ősz, 1. hf]] | ||
Írjon 2D útkereszteződés szimulátort. | Írjon 2D útkereszteződés szimulátort. | ||
| 270. sor: | 439. sor: | ||
===Második feladat=== | ===Második feladat=== | ||
[[ | [[File:Grafika_2010ő_hf2_1.jpg|thumb|300px|2010 ősz, 2. hf - ugrás előtt]] | ||
A Placcs családban három lány van, Placcs Bereniké, Placcs Cezarina és Placcs Nikodémia. Benediké 2D-s sziluettjét egyetlen Bézier görbével, Cezariáét egy Catmull-Rom spline-nal, Nikodémiáét pedig egy NURBS-szel írhatjuk le (vajon melyikük schlank?). | A Placcs családban három lány van, Placcs Bereniké, Placcs Cezarina és Placcs Nikodémia. Benediké 2D-s sziluettjét egyetlen Bézier görbével, Cezariáét egy Catmull-Rom spline-nal, Nikodémiáét pedig egy NURBS-szel írhatjuk le (vajon melyikük schlank?). | ||
| 276. sor: | 445. sor: | ||
A lányok normális testalkatúak, tehát egy-egy fejük, két-két lábuk, illetve kezük van. A lányokat hasonló referenciahelyzetben, célszerűen, de nem kötelezően, ugyanazokkal a vezérlőpontokkal definiáljuk. A Placcs család a 2D-s világban egy 10 m hosszú és 10 méter magas lakást birtokol, a kb. 3 méter magas lányok a világban kényelmesen elférnek egymás mellett. A lányok balettoznak, így ha nevük kezdőbetűjét lenyomjuk, akkor egy 1 méter magas grand jeté-t mutatnak be (= nagy, repülésszerű ugrás, horizontálisan szétvetett lábakkal) és a levegőben maradnak mindaddig, amíg rájuk nem klikkelünk. Ekkor visszatérnek a földre (a lányok lába a föld közelébe kerül, de nem kell tökéletesen pontosan a földön állniuk). A lányokat szivárvány színátmenettel kitöltött területekkel jelenítjük meg, ahol monokromatikus fényeknek megfelelő színek követik egymást, minden lánynál más irányban. | A lányok normális testalkatúak, tehát egy-egy fejük, két-két lábuk, illetve kezük van. A lányokat hasonló referenciahelyzetben, célszerűen, de nem kötelezően, ugyanazokkal a vezérlőpontokkal definiáljuk. A Placcs család a 2D-s világban egy 10 m hosszú és 10 méter magas lakást birtokol, a kb. 3 méter magas lányok a világban kényelmesen elférnek egymás mellett. A lányok balettoznak, így ha nevük kezdőbetűjét lenyomjuk, akkor egy 1 méter magas grand jeté-t mutatnak be (= nagy, repülésszerű ugrás, horizontálisan szétvetett lábakkal) és a levegőben maradnak mindaddig, amíg rájuk nem klikkelünk. Ekkor visszatérnek a földre (a lányok lába a föld közelébe kerül, de nem kell tökéletesen pontosan a földön állniuk). A lányokat szivárvány színátmenettel kitöltött területekkel jelenítjük meg, ahol monokromatikus fényeknek megfelelő színek követik egymást, minden lánynál más irányban. | ||
[[ | [[File:Grafika_2010ő_hf2_2.jpg|thumb|300px|2010 ősz, 2. hf - ugrás közben]] | ||
A 2D kamera (ablak), amelyen keresztül belesünk Placcsék lakásába, kezdetben a teljes szobát mutatja. A középső lány olyan magasra fog ugrani, hogy a kamerakép közepére kerüljön. SPACE lenyomására a kameránk mindig a következő lányt veszi célba (a lány, ha felugrott a kép közepén lesz), és a kamerán "látószöge" (a befogott tartomány) minden SPACE után kisebb lesz, azaz folyamatosan zoom-olunk. A referenciahelyzetből a világ aktuális helyére vivő modellezési transzformációt az OpenGL MODELVIEW, a kameratranszformációt pedig a PROJECTION transzformációjával kell megvalósítani. | A 2D kamera (ablak), amelyen keresztül belesünk Placcsék lakásába, kezdetben a teljes szobát mutatja. A középső lány olyan magasra fog ugrani, hogy a kamerakép közepére kerüljön. SPACE lenyomására a kameránk mindig a következő lányt veszi célba (a lány, ha felugrott a kép közepén lesz), és a kamerán "látószöge" (a befogott tartomány) minden SPACE után kisebb lesz, azaz folyamatosan zoom-olunk. A referenciahelyzetből a világ aktuális helyére vivő modellezési transzformációt az OpenGL MODELVIEW, a kameratranszformációt pedig a PROJECTION transzformációjával kell megvalósítani. | ||
| 288. sor: | 457. sor: | ||
===Harmadik feladat=== | ===Harmadik feladat=== | ||
[[ | [[File:Grafika_2010ő_hf3.jpg|thumb|300px|2010 ősz, 3. hf]] | ||
Készítsen mozgó pont fényforrással megvilágított csendéletet kétirányú sugárkövetéssel. | Készítsen mozgó pont fényforrással megvilágított csendéletet kétirányú sugárkövetéssel. | ||
| 313. sor: | 482. sor: | ||
===Negyedik feladat=== | ===Negyedik feladat=== | ||
[[ | [[File:Grafika_2010ő_hf4.png|thumb|300px|2010 ősz, 4. hf]] | ||
Írjon OpenGL programot, amely a Star Wars univerzum Rishi bolygóján egy rövid jelenetet mutat be. | Írjon OpenGL programot, amely a Star Wars univerzum Rishi bolygóján egy rövid jelenetet mutat be. | ||
| 438. sor: | 607. sor: | ||
Beadási határidő: 2009. 11. 03. 23:59 | Beadási határidő: 2009. 11. 03. 23:59 | ||
===Harmadik feladat=== | ===Harmadik feladat=== | ||
| 465. sor: | 630. sor: | ||
===Nagy házi feladatok tabló=== | ===Nagy házi feladatok tabló=== | ||
[[ | [[File:Grafika_2009ő_tabló.jpg|thumb|500px|2009 ősz, tabló]] | ||
[[Category:Infoalap]] | [[Category:Infoalap]] | ||
A lap jelenlegi, 2017. július 12., 15:26-kori változata
2015/1 őszi félév
Első feladat
Adott egy 1000m x 1000m-res mező, amelyet kezdetben a teljes viewport-ban látunk. Az egér bal gomb lenyomásával pontokat helyezünk el a mezőn. A pontokat piros belsejű, fehér körvonalú 5m sugarú körrel jelenítjük meg. Egyrészt a pontok egy fehér, önmagában zárt Catmull-Rom spline kontrollpontjai, amelyekhez tartozó időparaméter a lenyomáskori óra állás. Másrészt az első két pont egy egyenest definiál, a harmadik pedig egy fókusz pontot. A egyenes és fókuszpont által kijelölt parabola a síkot két részre osztja. A parabola fókuszpontot tartalmazó részében a hátteret sárgára, a másik részben türkizre színezzük ki. A Catmull-Rom spline és a parabola egyik metszéspontjában (már ha van) zöld színnel érintő egyenest rajzolunk mind a parabolához, mind pedig a spline-hoz.
A SPACE lenyomásának hatására a kamera ablak 500m x 500m-resre megy össze úgy, hogy a középpontja helyben marad. Ezután (2m/sec,3m/sec) kezdeti sebességgel vándorútra indul. Ha a kameraablak ütközik a mező szélével, onnan biliárd golyó módjára verődik vissza.
Minden, a feladat szövege által nem specifikált részlet szabadon megválasztható.
Második feladat
Készítsen sugárkövető programot, amely egy szobát és az abban mozgó üveg ellipszoidot jelenít meg mozgó pontszerű fényforrás megvilágítása mellett.
A virtuális világban a fény terjedési sebessége 1 m/s!!! (ezen feltételt mellőző megoldások nem fogadhatók el)
A szoba egyik oldala aranyból van, optikailag sima és forgásparaboloid geometriájú. A szoba többi oldala diffúz és valamilyen mintával textúrázott sík. A szoba mérete 10 m x 10 m x 10 m volna, ha eltekintenénk a paraboloid kitüremkedésétől.
Az üveg ellipszoid tengelyei a világkoordinátarendszer egyik tengelyével sem párhuzamosak. A leghosszabb tengely 2 m, a legrövidebb 0.5 m. Az ellipszoid egyenes vonalú egyenletes mozgást véget a szoba sarkából 0.5 m/sec sebességgel úgy, hogy legalább 10 másodpercig a szoba belsejében tartózkodik, mialatt a kamerából látható.
A pont fényforrás ugyancsak egyenesvonalú egyenletes mozgást végez úgy, hogy az első 10 másodpercben a szoba beljesében van.
A programnak a SPACE lenyomásának időpontjában keletkezett képet kell megjelenítenie.
Az arany törésmutatója és kioltási tényezője: r: 0.17/3.1, g: 0.35/2.7, b: 1.5/1.9
Az üveg törésmutatója és kioltási tényezője: r: 1.5/0, g: 1.5/0, b: 1.5/0
Harmadik feladat
Készítsen CSIRGURU BOMBÁZÓ játékot. A csirguru a csirke és a kenguru nászából született jószág, csirke teste, csőre, szemei, taraja van, valamint egy lába, amivel kenguruszerűen ugrál. A lába a csípőízületben nem fordul el, a térízületben hátra fordul, a bokában előre (amit a normál csirke esetében hajlamosak vagyunk előre hajló térdnek hinni). Az egy szem lábujj ugyancsak felfelé hajlítható, az ízületek tengelyei egymással párhuzamosak.
A csirguruk testét néhány zárt Bézier görbével definiált keresztmetszetek Catmull-Rom spline-t alkalmazó transzfinit interpolációjával kell létrehozni. A szem, csör, taraj, lábrészek ismert egyenletű paraméteres felületekből (pl. gömb, kúp, henger, paraboloid stb.) összerakhatók.
A csirguruk egy sík, textúrázott és megvilágított terepen a bomba aktuális helye alatt, a program indításától számított másodpercenként születnek meg, majd elkezdenek ugrándozni. A lendületvételi fázisban a csirguru feneke a földhöz közelít, majd a térdízület EGYENES VONALÚ GYORSULÓ MOZGÁST (inverz kinematika) végez, mialatt a lábujj a talajon marad, a térd pedig vízszintesen tartja a csirgurut. A bokaízület kiegyenesedése pillantában a csirguru elszakad a földtől és lendületvétel végén elért kezdősebességű ferde hajítással leírható pályán ugrik, a levegőben előreteszi a lábát, a földetérkezésnél pedig a lendületvételt visszafelé játsza le. Az ugrálást ismételgetheti, az egyes ugrálások között a haladási irányát ízlésesen változtatva.
A felhasználó egy bombát irányíthat a mező fölött egy síkban az A, W, D, Y billentyűkkel, majd SPACE-re a bomba leesik. Ha a bomba egy csirguru közelében esik le, a csirguru testrészei független ferde hajítást követnek, mialatt midegyik testrész egy-egy forgástengely körül forog.
A színteret egy irányfényforrás (nap) és ambiens fényforrás világítja meg, a csirguruk és a bombák a talajra árnyékot (síkra vetített árnyék algoritmus) vetnek.
2014/15 tavaszi félév
Első feladat
Készítsen elől-felül-oldalnézetes ortografikus 3D Renner spline görbeszerkesztőt, amelyben a pálya menti sebesség közelítőleg 1 m/sec. A 600x600 pixel felbontású alkalmazói ablak négy egyenlő részre van osztva, amelyekben az elől, felül és oldalnézetek látható, egy negyed pedig üres. A világ 3m x 3m x 3m-res kocka, amelynek középpontjában vettük fel az origót. A nézetekben a teljes világ vetületei látszanak, az origó értelemszerűen középen van. A transzformációkat „kézzel” kell számítani, az OpenGL mátrixok most még nem alkalmazhatók.
Amíg még nincs görbénk, az egyik nézetbeli egérkattintások kontrolpontokat vesznek fel, úgy, hogy a nézetre merőleges koordináta zérus. A további nézetekbe kattintva az ott legközelebbinek talált kontrollpont áthelyezhető, a nézetre merőleges koordináta változatlanul hagyásával. A pillanatnyi állapotot minden nézetben jelezni kell, a kontrolpontokat sárga körökkel, a 3D Renner spline-t pedig a fehéren rajzolt 2D merőleges vetületeivel.
A SPACE lenyomására egy kör indul el a görbe kezdőpontjából és a sebességvektorát farokként maga után húzva, kb. 1 m/sec pályamenti sebességgel végigcsúszik a görbén.
Második feladat
Készítsen sugárkövető programot, amely 100 mm oldalhosszúságú, egyik oldalán nyitott dobozban lévő durván tesszellált, optikailag sima, tükröző arany tóruszt, és egy Schwarzschild típusú (azaz töltés nélküli és nem forgó) Föld tömegű fekete lyukat tartalmaz. A doboz oldalai diffúz+spekuláris visszaverődésűek, a diffúz tag procedúrálisan textúrázott. A színteret ambiensfény és legalább egy pontfényforrás világítja meg. Élhet azzal az egyszerűsítéssel, hogy a fekete lyuk a fényt csak az első visszaverődés után görbíti, azaz a pont fényforrás és a megvilágított felület között nem, de a rücskös és sima felületek között, valamint a felületek és a szem között igen (a másik alternatíva a fényforrásból kilépő fény görbítésére a fotontérkép módszer). A fény elgörbülését kellő tudásszomj esetén Einstein téregyenletének Schwarzschildtól származó megoldásával, egyébként pedig az ekvivalenciaelv és a klasszikus newtoni gravitációs formula felhasználásával, sugármasírozással kell szimulálni. A rendelkezésre álló CPU idő 120 sec, szükség esetén kisebb bontású kép átmintavételezésével, távolságtól függő lépés-nagysággal és befoglaló térfogatokkal lehet a programot gyorsítani.
A szükséges fizikai állandók: A fény sebessége: 300 000 km/sec; A föld kerülete: 40 000 km; A nehézségi gyorsulás a föld felszínén: 10 m/sec^2.
Az arany törésmutatója és kioltási tényezője: r: 0.17/3.1, g: 0.35/2.7, b: 1.5/1.9 A falak diffúz és spekuláris visszaverődési tényezője és shininess paramétere, valamint a textúra szabadon megválasztható.
Harmadik feladat
Készítsen pingvin (Pygoscelis antarcticus) szimulátort. A pingvin teste a Geometriai modellezés diasor 25. diáján szereplő felosztási séma szerinti Catmull-Clark felosztott felület, amit négyszög hálóból minimum egy, de a teljes megoldáshoz legalább két lépéssel kell felosztani. A teljes megoldásban a 40. dián lévő half-edge adatstruktúrában kell a geometriát tárolni. A pingvin teste texúrázott, diffúz, a textúrakoordinátákat hengerkoordinátákból kell számítani (hengeres vetítés). A textúra maga procedurális. A pingvinnnek még két szeme van, csőre és két mozgatható merev vagy több ízületből összerakott lába van, amit felosztott felülettel vagy paraméteres felületekből kell kialakítani.
A havas terepen diffúz/spekuláris tojások vannak. Az avatár pinvginünket W=jobbra fordul, E=előre lép, R=balra fordul, SPACE=leül billentyűkkel lehet irányítani. Ha a pingvin 3 másodpercet ül egy tojáson, akkor a tojás kikel és egy újabb pingvin születik azon a helyen, amely őseihez hasonlóan rohan tojásokat kikelteni. A kamera az avatár pingvinre néz mindig, de poziciója állandó. A nap, lévén, hogy a Déli sarok közelébe vagyunk, lapos szögbe világítja meg a sík tájat, tojásokat és pingvineket. A síkon, síkra vetített árnyékok láthatók, amelyek feketék.
2014/15 őszi félév
Első feladat
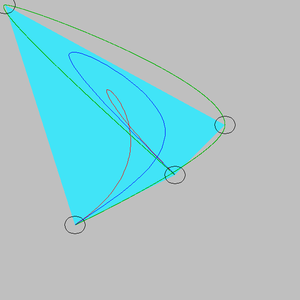
Készítsen „Síkon táncoló kontrollpontok” programot. A felhasználó az egér balgomb egyszeri lenyomással/elengedéssel veszi fel a kontrollpontokat (max 10-et), amelyekhez 2cm sugarú kisebb fekete köröket rendelünk. Ha a kontrollpontok száma legalább kettő, azokra egy türkiszkék színű, kitöltött konvex burkot, piros Bézier görbét, nulla kezdő és végsebességű, a kontrollpont lehelyezésének idejét paraméterként használó zöld Catmull-Rom spline-t és kék Catmull-Clark görbét illeszt.
A háttér világosszürke. Legnagyobb prioritása a kontrollpontoknak van, majd a görbék jönnek, végül jön a konvex burok.
Space lenyomására a kontrollpontok egy-egy 5 cm-es kör tetejéről elindulva, 5 másodpercenként egy teljes fordulatot téve, elkezdenek keringeni, mégpedig a páros indexűek az óramutató járásával megegyező, a páratlan indexűek pedig azzal ellentétes irányban. A konvex burok és a görbék követik a kontrollpontokat. Mindezt a felhasználó egy 58cm x 68 cm-es kameraablakon keresztül látja. Ha a felhasználó az egér jobb gombbal rábök egy kontrollpontra, akkor a kameraablakot ehhez köti, a kontrollpont elmozdulása automatikusan a kameraablakot is arrébb viszi.
Második feladat
Készítsen csendéletet, ahol procedurálisan textúrázott, diffúz+Blinn spekuláris asztalon optikailag sima tárgyak, egy ellipszoid aranykaktusz, egy paraboloid ezüstkaktusz és egy henger üvegkaktusz áll (a háromból min. kettő megvalósítása szükséges). A kaktuszoktörzséből a törzzsel hasonló, de kisebb részek nőnek ki, mindig a felületre merőlegesen, legalább két további szinten (az összes részek számát úgy kell megválasztani, hogy a program 1 percen belül lefusson). A kinövő részek véletlenszerűen, nagyjából egyenletesen oszlanak el a felületen. A teret egy zöldes, egy kékes, és egy pirosas pontfényforrás világítja meg, a megvilágítási intenzitás a távolság négyzetével csökken. Az égbolt világoskék. Árnyékok vannak. A kamera az asztal fölött van és enyhén lefelé néz.
A sugár-objektum metszéspontot és a normálvektort a metszéspontban analitikusan kell számolni.
Az említett anyagok törésmutatója (n) és kioltási tényezője (k):
...................r..........g..........b
Üveg (n/k)......1.5/0.0, 1.5/0.0, 1.5/0.0
Arany (n/k).....0.17/3.1, 0.35/2.7, 1.5/1.9
Ezüst (n/k).....0.14/4.1, 0.16/2.3, 0.13/3.1
Harmadik feladat

Készítsen szimulátort műhold befogáshoz a Мир űrállomás számára! A fényforrás a távoli nap. Az űrállomás a csillagos égbolt előtt, egy diffúz, procedurálisan textúrázott bolygó körül kering, pályája nem geostracionárius. A bolygót átlátszó kékes légkör veszi körül. Az űrállomás teste fémes csillogású forgástest, a sziluett Catmull-Rom spline-nal adandó meg. Az űrállomáson van egy nagyjából kör alakú lyuk. Az űrállomáshoz legalább két napelem tábla tartozik. Az űrállomás egy, a fő tehetetlenségi iránytól különböző tengely körül lassan forog.
Az avatárunk éppen űrsétát végez, magát az űrállomáshoz kötve egy hosszú gumikötél végén rángatózva. A gumikötél csak egy adott távolság után feszül meg, azon túl Hooke törvény szerint nyúlik. Az űrállomástól nem zérus sebességgel rúgtuk el magunkat. Avatárunk tömege az űrállomás tömegénél sokkal kisebb. Az avatár mindig az űrállomás nyílása felé néz.
A mesterséges hold gömb alakú, amiből legalább három henger vagy kúp alakú fúvóka nyúlik ki (bónusz: ha a fúvókák tengelye nem megy át a súlyponton, akkor a forgását is szabályozhatjuk). Kezdetben a műhold az űrállomáshoz képest lassan halad és forog. A műhold ugyancsak diffúz-spekuláris, a fúvókák színe alapján vezérelhetjük őket. Ha a q, w, ... billentyűket lenyomjuk, a betűhöz rendelt fúvókán egy lángnyelv tör ki, a műhold pedig ellentétes irányú I impulzust kap. A lendület és perdület, mint mindig, itt is megmarad.
A játék célja, hogy a mesterséges hold az űrállomás nyílásán besétáljon.
A harmadik feladat a játék "csendélete", még nem kell az objektumokat animálni és lángnyelvet sem kell kilőni. A virtuális világ életre keltése és vezérlése a negyedik házi feladata lesz.
Negyedik feladat
Egészítse ki a 3. feladatot az ott specifikált felhasználói beavatkozási lehetőségekkel és animációval.
2013/14 őszi félév
Első feladat

Készítsen "Kaksiulotteisia vihaisia lintuja" programot, amelyben egy piros és egy zöld madár szerepel, valamint világos zöld talaj, a talajból kiálló tetszőleges színű kétágú csúzli, amely fekete színű széles gumival fogja körbe a kilövendő piros madarat. A csúzli tára, ahol a piros madár várja a sorsa beteljesülését, a 600x600 felbontású alkalmazói ablak bal felső sarkához képest 200 pixellel jobbra és 400 pixellel lejjebb van.
A madarak teste, szeme és szemgolyója ellipszis (nem kör!), csőrük, farktollaik és szemöldökeik háromszögek. Szárny és bóbita opcionális. A zöld madár fel-le repked akár szárnyak nélkül is, magassága az időben szinuszosan változik az ütközésig. A piros madarat csúzliból lehet kilőni a fizikai törvényeknek megfelelően, a csúzli rugóenergiáját teljes mértékben átveszi a madár induláskor. A kilövés folyamat azzal kezdődik, hogy az egér bal gombjának lenyomásával a madár ellipszis alakú testének belsejébe klikkelünk, amikor a madár a kurzorhoz ragad és követi az kurzor mozgását az egérgomb elengedéséig. A csúzli gumija végig szorosan feszül a madár fenekére. Amikor elengedjük a bal gombot a piros madarat is útjára bocsátjuk, azaz kirepül a csúzliból. Perdülettel és forgással nem kell foglalkozni. A piros madárra reptében a nehézségi erő hat, közegellenállás és felhajtóerő (nincs szárnya, amivel csapkodna) pedig nincs. Ha a piros és a zöld madár ellipszis teste ütközik (figyelem, két ellipszis ütközését pontosan kell számítani), mindketten megállnak a levegőben és a piros madár sárgává változik. Ha a piros madár kirepül a látható tartományból, automatikusan születik egy új a csúzliban fejjel lefelé a két ág "között".
A feladat megoldásához csak az előadáson eddig szerepelt OpenGL függvények használhatók, azaz: glBegin, glEnd, glColor, glVertex, glViewport.
Figyelem: a keret változott, ezért a korábbi évek kereteit nem lehet használni.
Beadási határidő: 2013. 10. 01. 23:59 (Kiadás dátuma: 2013.09.18.)
Második feladat
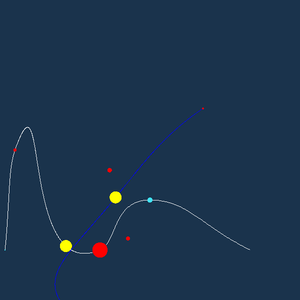
Készítsen 2D editort, amivel egy 100m x 100m-es területet lehet berendezni, amelybe egy 50m x 50m-es ablakú kamerával nézünk bele. Az ablakot minden ‘s’ lenyomásra a (10, 20) vektor tolja el. Ha az ablak elérte a terület szélét, akkor visszaugrik a bal alsó sarokba. A program a bal egérgomb lenyomásainak helyét kontrollpontnak, az lenyomás pillanatában az óra állását pedig csomóértéknek (kontrollponthoz rendelt paraméterértéknek) tekinti, így minden bal egérgomb lenyomással egy újabb kontrollpontot vehetünk fel (max 10 kontrollpontra kell a programot felkészíteni). A kontrollpontokra egy fehér Tenziós Catmull-Rom (TCR) spline-t illeszt, ahol a tenzió mindenhol -0.5. A kontrollpontok nyugalmi állapotukban 1m sugarú piros kitöltött körök.
Space lenyomására a program aktivizálódik, a spline-t megduplázza és az új változatot 60 fokkal a kontrollpontok súlypontja (aminek koordinátáit a kontrollpontok koordinátánkénti aritmetikai közepeként számíthatunk) körül elforgatja, majd kék Bézier görbét csinál belőle (mialatt az eredeti TCR marad a helyén). Ezután egy-egy 1 m sugarú sárga kitöltött kör indul el minden görbén, mégpedig a TCR-n a paraméterezésnek megfelelő időzítéssel, azaz annyi idő alatt ér a görbe végére, ameddig a kontrollpontot felvétele tartott. A Bézier-t a saját köre úgy futja be, hogy ugyanakkor érkezzen a végére, mint a TCR-n szaladó társa. A futamok újra kezdődnek. A futás alatt a kontrollpontokat ábrázoló kitöltött körök sugara folyamatosan változik amivel azt mutatják, hogy milyennek kell lennie az ide elhelyezett súly abszolút értékének, hogy a görbe aktuális pontját a kontrollpontok ilyen súlyokkal vett kombinációjaként kapjuk meg (Bézier-nél nyilván a Berstein polinom, TCR-nél érdemes gondolkodni egy kicsit). Ha a súly pozitív, a kör piros. Ha negatív, akkor türkisz kék.
Figyelem: csak közelítőleg C2 folytonos és egzaktul C1 folytonos valódi, nem egyenletes TCR spline elfogadható, pl. Catmull-Rom és felesleges dolgokat tartalmazó Kochanek-Bartels nem. Közérthetőbben: az Internetről másolt spline-ok ellenjavaltak.
Beadási határidő: 2013. 10. 20. 23:59 (Kiadás dátuma: 2013.10.04.)
Harmadik feladat

Készítsen négyhengeres sugárkövető programot. Az 1. henger tartalmazza a teljes színteret, fala optikailag sima arany, alapja megválasztható színű diffúz, teteje hiányzik, amin a fehér égbolt világít be (ezt úgy lehet figyelembe venni, hogy azok a sugarak, amelyek kilépnek a hengerből ilyen sugársűrűséggel térnek vissza). A többi henger az 1. belsejében van, tengelyük sem egymással, sem bármelyik koordinátatengellyel nem párhuzamos. A 2. anyaga optikailag sima ezüst, a 3. anyaga optikailag sima réz, a 4. anyaga optikailag sima üveg, gyémánt vagy megválasztható színű diffúz lehet. Az homogén égbolton kívül még egy vagy több optikailag sima ezüst forgásparaboloid reflektorú, nem a fókuszba helyezett pontszerű fényforrás világítja meg a teret.
A kamerát úgy kell elhelyezni, hogy a hengerek láthatók legyenek. Fotontérképet nyilván csak a diffúz felületekhez kell rendelni az optikailag sima felületekhez nem. A fotonok számát úgy kell beállítani, hogy a program 1 percen belül 1 CPU magon lefusson (ha ezt az időt túllépi, a fotonszámot érdemes csökkenteni, pl. úgy, hogy ne legyen 10^4-nél lényegesen nagyobb, de a nem lépi túl, akkor lehet több fotonnal is dolgozni). A fotontérkép felbontását pedig úgy kell meghatározni, hogy a kausztika az adott fotonszám mellett sima legyen.
Anyagtulajdonságok:
Optikailag sima anyagok:
...................r..........g..........b
Üveg (n/k)......1.5/0.0, 1.5/0.0, 1.5/0.0
Gyémánt (n/k)...2.4/0.0, 2.4/0.0 2.4/0.0
Arany (n/k).....0.17/3.1, 0.35/2.7, 1.5/1.9
Réz (n/k).......0.2/3.6, 1.1/2.6, 1.2/2.3
Ezüst (n/k).....0.14/4.1, 0.16/2.3, 0.13/3.1
Diffúz anyagok: kd(r,g,b) tetszőlegesen, jó ízléssel megválasztható.
Beadási határidő: 2013. 11. 10. 23:59 (Kiadás dátuma: 2013.10.25.)
Negyedik feladat

Készítsen OpenGL programot, amely egy (fekete foltos textúrájú), de alapvetően fehér diffúz+spekuláris testű Szalámi Gólyát és zöld diffúz+erősen spekuláris testű (nyálkás) Ellipszoid Békákat jelenít meg diffúz, textúrázott terepen. A Szalámi Gólya onnan ismerszik meg, hogy ha testét a Catmull-Rom spline vázára merőlegesen bárhol kettészeljük, akkor a metszet kör alakú (a váz definíciója: ha a Szalámi Gólya testének minden felületi pontját egyszerre gyújtjuk meg, akkor a tűzfrontok a vázban találkoznak). A kör sugara a váz mentén változik, amelyet egy másik Catmull-Rom spline-nal kell megadni. A gólyának és a békáknak is két-két szemük van, a gólyának még piros kúp alakú csőre és két gólyalába van (amelyek biológiai ismereteink szerint, a mi lábunkkal ellentétben, térdben előre és nem visszafelé hajlíthatók). A gólya arányai olyanok, hogy előrehajolva a csőrének végével elérné a talajt. Az Ellipszoid Békák testrészei ellipszoidok. A terep textúrázott, nem szükségképpen sík. Tereptárgyak tetszés szerint megválaszthatók. A színteret a nap (irányfényforrás) az ég (ambiens fényforrás) és egy energiától duzzadó szentjános bogár (pontfényforrás) világítja meg.
Beadási határidő: 2013. 12. 04. 23:59 (Kiadás dátuma: 2013.11.20., Beadási határidő először: 2013. 12. 01. 23:59, majd kitolva a határidő: 2013.12.03.; UTÁNA szerverprobléma miatt: 2013.12.04. 23:59)
Ötödik feladat

Mozgassa meg a 4. házi objektumait. A gólya lépeget előre 1 lépés/sec sebességgel. A támaszkodó láb nem csúszkál (inverz kinematika). A ‘J’ billentyű lenyomására 0.5 sec alatt 10 fokot jobbra fordul célszerűen a támaszkodó láb körül, hasonlóan a ‘B’ billentyű lenyomására balra. A SPACE hatására a nyakát előrehajtva lecsap és ha békatestet talál (végtagok nem számítanak), akkor a béka eltűnik. A gólyát csontváz animációval kell mozgatni, a lábrészek és a nyak hossza nem változhat a mozgás során. A láb részei tekinthetők merev testnek, de a gólyatest nem, így azt a csontvázra "bőrözni" kell. A békák merev testként akár véletlen irányokba ugrálhatnak, de két ugrás között 1 sec rákészülési időre van szükségük. A terepet illetően két lehetőség közül lehet választani. Az elsőben a terep sík és akkor a testeknek van árnyékuk rajta, amit a nap vet (síkra vetített árnyék algoritmus). A másik lehetőség, hogy a terep nem sík.
Beadási határidő: 2013. 12. 16. 11:00 (Kiadás dátuma: 2013.12.04.)
2012/13 tavaszi félév
Első feladat
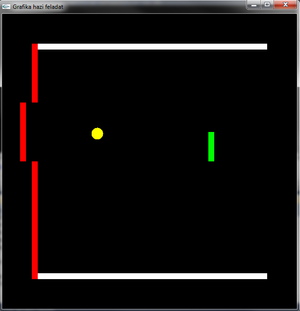
Készítsen breakout játékot, fejet hajtva a játékfejlesztés úttörői előtt.
A 2D squash szobának három oldala van, mérete 40x40 méter. A falak 1 m vastagok. A fehér oldalfalak jól oda vannak betonozva, a piros hátsó fal téglái azonban kiüthetők (a téglák száma megválasztható, de legalább 5 és a tégla területe, és így a tömege a labdáénál nagyobb kell hogy legyen, hogy vissza tudja lökni a labdát).
A játékosnak egy 4 m magas, 1m vastag téglalap alakú ütője van, amit az 'i' (föl), 'j' (balra), 'k' (jobbra) és 'm' (le) billentyűkkel mozgathat. A szobában egy 1 m sugarú sárga, köralakú labda pattog, vízszintes kezdősebessége 10 m/s, függőleges kezdősebessége 2 m/s, a falakkal rugalmasan ütközik (energia és impulzus megmarad). Az zöld ütő gyorsítja a labdát, egy ütéstől a mozgási energia 20%-kal nő.
Az ütő sarkai le vannak gyalulva, azaz az ütközési normális a sarkon 45 fokos, ami lehetőséget ad arra, hogy az ütő sarkával is odasózzunk a labdának. A hátsó fal téglái az ütközés hatására a fizikai törvényeknek megfelelően kirepülnek. Súrlódás nincs. A szobát felülnézetből látjuk, a 2D kamera a szobán túl még egy 5 méteres sávot is befog.
A használható OpenGL függvények: glBegin, glColor, glVertex2f, glEnd, glClearColor, glClear, glViewport, glMatrixMode, glLoadIdentity, gluOrtho2D.
Extra élvezet profiknak: ne csak az impulzus, hanem a perdület is maradjon meg az ütközésnél.
Beadási határidő: 2013. 03. 10. 23:59
Második feladat
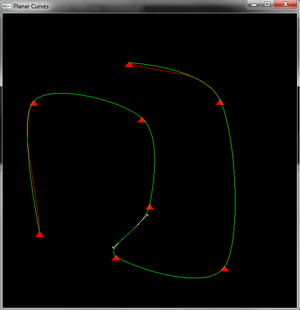
Készítsen 2D editort, ami az egér balgomb lenyomásokat kontrolpontokként értelmezi, amelyekre egy piros Catmull-Rom (CR) spline-t és egy zöld CRI-spline-t is illeszt.
A CRI spline interpolációs, a CR-hez hasonlóan harmadfokú és a kontrolpontokban C1 folytonos, másutt C2 (ezen feltételek nem teljesítése automatikus elutasítást von maga után). A CRI sebességvektora az i. kontrolpontban a megelőző és a következő kontrolpontok közötti átmenet átlagos sebessége (p[i+1]-p[i-1])/(t[i+1]-t[i-1]) (széleken megválasztható).
A görbék a csomóértékeken közösködnek, amelyek az i. pont esetén t[i]=i+sin(i/5.0)*0.4.
A ‘Z’ „zoom”-ol, azaz a kameraablak mérete felére csökken mialatt a közepe helyben marad, a ‘P’ pedig „pan”-nel, azaz a kameraablak a vízszintes méretének 10%-val balra, függőleges méretének 20%-val felfelé mozdul el. A két görbén egymással szemben periódikusan egy-egy nyíl szalad, a kezdőpontja a görbe adott időponthoz (sec-ben) tartozó pontja, egyébként pedig a sebességvektor skalárszorosa (látható legyen a képen).
Beadási határidő: 2013. 03. 24. 23:59
Harmadik feladat
Jelenítsen meg egy piros-fehéres abroszon álló teli söröspoharat sugárkövetéssel! A színtérfelépítéséhez kizárólag általános kvadratikus felületeket (4x4-es szimmetrikus mátrixot), féltereket és halmazműveleteket használhat. A söröspohár a talpával stabilan áll az abroszon. Feltételezheti, hogy a látható tartomány minden hullámhosszán az üveg törésmutatója 1.5, a söré pedig 1.3. Az üveg és a sör hullámhossz függő hatáskeresztmetszetét "méréssel" állapítsa meg közelítőleg (figyelem, dimenzió)! A csendéletet világoskék ég és egy intenzív sárgás pontfényforrás világítja meg. A kamerát úgy kell felvenni, hogy az abrosz egy része és a söröspohár teljes szépségében pompázzon. Örömmel fogadjuk, ha a sörben levegőbuborék vannak, az abroszon pedig kausztika, de ezek nem kötelezők.
Beadási határidő: 2013. 04. 14. 23:59
Negyedik feladat
Készítsen virtuális világot csempézett szobával, fókával és labdával. A padló textúrázott, diffúz/spekuláris csempe jellegű anyag. A fóka teste szabadformájú paraméteres felület (pl. Largange interpolációs felület, Bézier felület, nem klasszikus felület paraméteres formában), nem texúrázott, fekete, de spekulárisan csillogó. A fókának két szeme van, amelyeket forgathat, de a szemgolyók nem ugranak ki a szemgödörből. A strandlabda textúrázott és illuminált sárga-piros csíkos gömb.
A szobában legalább egy pont vagy irányforrás világít (lehet több is). Az 'f' billentyűvel a kamerát egy lépéssel előre, a 'b'-vel pedig hátra vihetjük.
Beadási határidő: 2013. 05. 05. 23:59
Ötödik feladat
A 4. feladat fókájába tegyen egy csontvázat (legalább két csont) és az ízületben végrehajtott elforgatást kösse az 's' (balra), 'd' (jobbra), 'e' (fel), 'x' (le) billentyűkre. Az 'a'-ra a fóka kicsit előrecsúszik, 'y'-ra hátra.
A csontvázhoz kösse a fóka tesszellált bőrét (rigid binding), mégpedig úgy, hogy egy csúcsponthoz a legközelebbi csont tartozzon. A bőr követi a csontot, azaz elszenvedi annak transzformációját.
A fókának fejelgetnie kell, azaz úgy kell irányítani a fókát, hogy a labda fején pattogjon. Az ütközésdetektáláshoz a fóka fejét közelítheti gömbbel. Az ütközés rugalmas, a fókafej sebessége a labda sebességéhez képest elhanyagolható. Kezdetben a labda éppen a fóka feje fölött van. A fóka két szeme mindig a labdára szegeződik.
Beadási határidő: 2013. 05. 19. 23:59
2012/13 őszi félév
Első feladat
Hansel és Gretel hegyes-völgyes, 10km x 10km-es négyzet alakú, kerítéssel körbevett erdőben rohangál (gyorsan), ahol elvesztették egymást.
A legmélyebb völgy tengerszint feletti magassága 250m, a legmagasabb hegycsúcsé 1014m. A terep magasságát tetszőleges differenciálható, egynél több lokális minimummal és maximummal rendelkező függvénnyel definiálhatja, ami célszerűen különbözik a közeli barátok függvényeitől.
Az erdő egy (pszeudo) véletlenszerűen kiválasztott pontján egy 20 m magas torony tetején mobiltelefon antenna található. A 't' billentyű lenyomásának hatására a telefontársaság egy brigádja kiszáll és egy szempillantás alatt egy másik (pszeudo) véletlen pontra telepíti a tornyot. Hansel az egér bal gomb lenyomásának helyét, Gretel pedig a jobb gomb lenyomásának helyét célozza meg, újabb egéreseményeknél irányt váltanak, a kerítéshez érve billiárd golyóhoz hasonlóan visszaverődnek.
Értelemszerűen Hansel és Gretel a terepen halad. Hansel és Gretel terepmenti sebessége (figyelem, ez nem egyezik meg a felülnézetből észlelt sebességgel) V*(1-M/90), ahol V=1000 m/s a vízszintes talajon elérhető sebesség, M pedig a terep meredeksége fokban (lejtő esetén a meredekség negatív). A meredekséget a függvényből szimbolikus deriválással (azaz nem differenciahányados közelítéssel) kell számítani, célszerűen saját kézzel, nem pedig valamely matematikai csomag felhasználásával.
A világ aktuális állapotát felülnézetből kell megjeleníteni, ahol a terepet szürkeárnyalatos képként ábrázoljuk, a legmagasabb pont fehér, a legalacsonyabb pont fekete, a közbenső magasságok pedig arányosan szürkék. Hansel és Gretel a Mars, illetve a Vénusz jelét kapják, Hansel világoskék, Gretel pedig rózsaszín. A bolygók jelében található köröket százszöggel kell közelíteni. A torony felülnézetben egy sárga háromszögnek látszik. A feladat azon pillanatok azonosítása, amikor Gretel mobilozhat Hanselnek, azaz, amikor mindketten rálátnak az antennára. Ekkor a torony, Hansel és Gretel között egy piros háromszöget kell kirajzolni. A fénykép tetején egy progress-bar mutatja, hogy az idő hányad részében tudta elérni Gretel Hanselt.
A feladatot diszkrét-idő szimulációval kell megoldani, ahol a mintavételi idő 100 msec. A láthatóságot sugármasírozással (ray-marching) lehet ellenőrizni, legfeljebb 100m-res lépésközt alkalmazva.
Második feladat
Középfölde királya új görbét talált fel, amit szerénytelenül KK-spline-nak nevezett el.
A következőképpen okoskodott: Minden egymás követő három vezérlőpontra egy másodfokú paraméteres görbét illesztünk, így két vezérlőpont között, a legelső és legutolsó párt kivéve, mindig két másodfokú paraméteres görbe látható, amelyek legyenek A és B. Egy másodfokú paraméteres görbe három pontját rendre kezdő, középső és megint kezdő pontnak hívjuk. Két vezérlőpont között az egyik vezérlőpont az A görbének a középső pontja a B görbének pedig a kezdő pontja. A másik vezérlőpont ugyanakkor a B görbének a középső pontja és az A kezdőpontja. A két görbeívből csináljunk egyetlen görbét konvex kombinációval úgy, hogy a középső pontban a másodfokú paraméteres görbe súlya 1, a kezdő, illetve végpontban pedig 0, közöttük pedig lineárisan változik.
Középfölde királya szeretné, ha a görbéje kiszorítaná a Catmull-Rom spline-t, ezért Önt kérte meg, hogy egy rajzolóprogramot írjon, demonstrálandó találmánya nagyszerűségét.
A rajzolóprogram a világot 0..1000 x 0..1000 mm-es négyzetben tárolja (ez felelne meg Powerpoint-ban a slide-nak), ezen kívül nem lehet rajzolni. Kezdetben a kameraablak bal alsó sarka a világ (100,100) koordinátájú pontjában van, a jobb-felső sarka pedig az (500,500) pontban. A rajzolóprogram az egér bal gomb lenyomására egy-egy újabb kontrollpontot vesz fel. A vezérlőpontok maximális száma 100. A vezérpontokhoz rendelt paraméterértékek tetszőleges olyan növekvő sorozatot alkothatnak, amelyben a növekmény az összes korábbitól különböző (pl. nem jó: 0,1,2,...; jó: 1, 2, 4, 7...). A kontrollpontokra KK-spline-t, és az összehasonlítás érdekében Catmull-Rom spline-t illeszt a program, és a teljes paramétertartományt 1000 részre osztva vektorizál, majd töröttvonalként rajzolja fel a két görbét. A KK-spline piros színben, a Catmull-Rom spline zöldben jelenik meg, ahol takarnák egymást, ott a KK-spline-nak van prioritása. Az egér jobb billentyűjének lenyomásával a görbéket ki lehet választani. Akkor választunk ki egy görbét, ha a vektorizált töröttvonal a kurzor körüli 5x5 pixel méretű négyzetet átmetszi. Ha egyszerre választjuk ki a KK-spline-t és a Catmull-Rom spline-t, akkor a KK-spline-nak van prioritása. Az egér jobb gomb újbóli lenyomása a kiválasztott görbét a két jobb klikk közötti elmozdulásnak megfelelően eltolja. A világba belezoomolni a z betű lenyomásával lehet, amikor a kurzor jelenlegi helye nem mozdul el, de a kamera ablak a zoom előtti mérethez képest tized akkorára esik össze, azaz a világ elemei a korábbihoz képest tízszer nagyobbnak fognak látszódni. Egymás után többször is lehet belezoomolni, amikor egyre nagyobb nagyítás érhető el. A kizoomolás művelet nem kötelező műsorszám, de igény esetén Z betűre megvalósítható.
Harmadik feladat
Készítsen kétirányú sugárkövető programot, amely egy diffúz barnás téglalap asztalon álló üvegtéglába zárt aranytóruszt jelenít meg.
A tórusz az üvegben egy levegőbuborék belsejében helyezkedik el. A buborék választható ellipszoidnak, gömbnek, vagy akár téglatestnek is. A tóruszt geometriailag max 100 db, árnyalónormálokkal ellátott háromszögre kell bontani. A visszaverődési irányok számításánál a lineárisan interpolált árnyalónormállal kell dolgozni. A színteret az egy fehér pontfényforrás világítja meg, amely egy félgömb irányaiban egyenletes sugársűrűséggel világít. A színteret világos színű égbolt veszi közre, amely minden irányban egyenletesen sugárzó fényforrásként viselkedik. A fényforrások teljesítménye tetszőleges, pozitív értékre állítható, a cél, hogy a kép szép legyen. A kausztikus jelenségek kezelése miatt a lövőfázis a pontfényforrásból 10000 sugarat indít, amelyekből a simafelületekkel találkozottak végül az asztalhoz rendelt fotontérképben tárolja. A fotontérképpel indirekten és a fényforrással direkt módon megvilágított színteret sugárkövetéssel fényképezze le. A számított sugársűrűségeket lineáris vagy akár nem lineáris tone-mapping alkalmazásával kell a megjeleníthető dinamikai tartományba konvertálni.
Szépségverseny: A fényforrás, illetve az alakzatok mozgatásával video készíthető, amellyel szépségversenyen lehet indulni. Itt a paraméterekre semmiféle korlátozás sincs.
Negyedik feladat
Készítsen helikoptert és alatta elterülő tájat. A helikopter (http://hu.wikipedia.org/wiki/Helikopter) háromszöghálóból, ellipszoidből és hengerből összerakott testtel rendelkezik, kétágú, forgatható főrotorja van (egy lapát egy téglatest), és háromágú csak kisebb farok rotorja.
A helikoptert a RPY szögeivel lehet kormányozni: R-E a roll, P-O a pitch, Y-X pedig a yaw szöget növeli, illetve csökkenti 20 fokkal. A virtuális kamera a helikopter felett van valamivel és kissé lefele néz, úgy, hogy az optikai tengelye a helikopter közepén átmenjen. A helikopter teste diffúz-spekuláris khaki-színűre van festve, a pilótafülke átlátszó, spekuláris, a forgólapátok szürke spekuláris jellegűek.
A helikopter pillanatnyi orientációját a kvaterniójának a megjelenítésével is megmutatjuk. Egy kvaterniót a helikopter közepéből induló piros diffúz-spekuláris nyíllal láttatjuk (nyíl=henger + a végén kúp), amelynek iránya párhuzamos a kvaternió képzetes részének irányával, hossza pedig arányos a valós rész abszolút értékével. Az arányossági tényezőt úgy kell beállítani, hogy 90 fokos elforgatásnál a nyíl kb. kétszer hosszabb legyen a helikopter hosszánál.
A tájat egy nagy tesszellált téglalapból kell létrehozni, amelyet procedúrális (!) textúrával látunk el. A tájon elszórt épületek állnak
A helikoptert és a tájat a nap (irányfényforrás) és az ég (ambiens fényforrás) világítja meg.
Ötödik feladat
Animálja a 4. feladat helikopterét a következőképpen. A fő és mellékrotor állandó szögsebességgel forog. Az R,P,Y (nagybetűkkel!) szögek a helikopter aktuális koordinátarendszeréhez képest értendők, azaz a helikopter saját magához képest kormányozzuk. A helikoptert két kormányzás között egyenesvonalú egyenletes mozgást végez előre, és egy a helikopterhez gumikötéllel odakötött, léggömbön függő kamerával követjük. A léggömbből adódó felhajtóerő állandó, a légellenállás a sebességgel arányos. A kamera mindig a gumikötés húzásának irányába néz. SPACE billenntyű lenyomására a helikopter egy gumilabdád lő ki, amely a terepen pattog, a "bounciness" 0.9, azaz az ütközéskor a merőleges sebesség abszolút értéke az eredeti 90 százaléka lesz.
2011/12 őszi félév
Első feladat
Készítsen 2D giliszta üldözéses játékot OpenGL-ben.
Két játékosunk és gilisztánk van, az egyik giliszta zöld, a másik piros. A giliszták teste szinusz hullám, amelyet vonallal, háromszög vagy négyszög szalaggal lehet felrajzolni. A giliszták feje sokszög. Az egyik játékos célja, hogy a piros giliszta érje utol a zöldet, a másiké, hogy megakadályozza ezt.
A giliszták három szinten mozoghatnak, a szintek között a két játékos egy-egy lifttel viheti át őket (Bal lift fel/le = q/a, a jobb lifté pedig o/l). A giliszták gilisztamozgással haladnak előre (nyújtáskor a farkuk vége, összehúzódáskor a fejük mozdulatlan, közben a hosszuk megközelítőleg állandó), és a falnál hátra arcot csinálnak. A giliszta akár egyetlen pontján is képes kapaszkodni, ha viszont egyetlen ponton sem támaszkodhat, leesik és az alsóbb szinten folytatja a mozgását a korábbi irányban.
A játék befejeződik, ha valamely gilisztát a lifttel agyonnyomjuk, vagy a piros utoléri a zöldet.
Beadási határidő: 2011. 09. 26. 23:59
Második feladat
Készítsen üde zöld füves versenypályát kb. 4 cm-es 2.5 dimenziós atlétacsigák (Gastropoda Athleta Dimensio II.V) számára! Az atlétacsiga az éticsigával ellentétben bedől a kanyarban, lassításkor előre, fékezéskor hátra hajol, általában a rá ható erő irányába és azzal arányosan dönti a testét. Az atlétacsiga 2.5 dimenziós volta annyit jelent, hogy ugyan 2 dimenziós görbék által kitöltött területekből áll, de a görbék kontrolpontjainak van z koordinátája is, amely alapján a pont elmozdul az x,y síkon az erővel és a z koordinátával arányosan. A test határa zárt Catmull-Rom spline (amiből a vektorizáció konkáv sokszöget hoz létre, melyet fülvágó algoritmussal kell háromszögekre bontani), a szemek határai zárt Bézier görbék, a ház több Catmull-Clark subdivision görbével határolt sokszög. Az atlétacsiga referenciapontja (pivot pont) a referenciahelyzetében az origó, hossztengelye az y tengely (a referenciapont kerül mindig a pálya fölé, és e körül fordul el az atlétacsiga a haladási irányba). A csigát - a saját érdekében – a kontrolpontokon végrehajtott saját skálázással és elforgatással, majd a csúcspontokon glTranslatef függvényekkel kell pályára helyezni. A pálya ugyancsak zárt Catmull-Rom spline, hossza kb. 1 méter, a vezérlőpontokat POINT primitívekkel lehet felrajzolni. A virtuális világban az egységet cm-re kell választani. Az atlétacsiga a pályagörbe paraméterét egyenletesen változtatva mozog a pályán, 5 másodperc alatt ér körbe. Az egér bal gombjának lenyomása a pálya kurzorhoz legközelebbi kontrolpontját a kurzor aktuális helyére mozdítja. A kamera induláskor az egész pályát befogja, a z betű lenyomásával viszont rázoomol a csigára és követi a pályáján. A kamerát a gluOrtho2D függvénnyel kell implementálni. A Catmull-Rom és Catmull-Clark kötelező műsorszám. A fülvágás, Bézier görbe, interaktív pályamódosítás és zoom részfeladatokból mind megpróbálandó, de ezekből kettő lehet hibás is, attól még elfogadjuk a feladatot.
Kiadási határidő: 2011. 09. 27. Beadási határidő: 2011. 10. 14. 23:59
Harmadik feladat
Ajándékozzon arany- vagy rézgyűrűt (az anyag megválasztható) virtuálisan, valamint opcionálisan gyémántot is!
A gyűrű egy sima felületű, azaz ideális tükörként viselkedő henger. A gyűrű egy diffúz, mintás, téglalap alakú asztalon fekszik. A mintázat azt jelenti, hogy a diffúz visszaverődési tényezőt egy alkalmasan választott függvénnyel kell előállítani, amely függ az asztalon lévő pontos helytől (procedurális textúra). A virtuális világot világoskék ambiens fény és egy fehér pont- vagy irányfényforrás (tetszés szerint választhatunk a pont és irányfényforrás között) világítja meg. Az opcionális gyémántot egy ellipszoid alakú kőből csiszolták, azaz poliéder, ami az ellipszoid tesszellált változata. A gyémánt felületek simák, ideális tükörként és törő felületként viselkednek.
A gyűrű és az opcionális gyémánt kausztikus foltokat ejt a diffúz mintás asztalon. A kamerát úgy kell elhelyezni, hogy a kausztikus foltok, árnyékok és a tárgyak szépen láthatók legyenek a keletkező képen.
A törésmutató (n) és kioltási tényező (k) az r, g, b hullámhosszain:
r g b Gyémánt (n/k) 2.4/0 2.4/0 2.4/0 Arany (n/k) 0.17/3.1 0.35/2.7 1.5/1.9 Réz (n/k) 0.2/3.6 1.1/2.6 1.2/2.3
Az opcionális gyémánt nélkül is elfogadjuk a feladatot, ha a többi rész jó.
Beadási határidő: 2011. 11. 13. 23:59
Negyedik feladat
Építsen fel egy virtuális világot csirkével és úthengerrel, és jelenítse meg OpenGL környezetben.
A virtuális világ elemek:
- Csirke: paraméteres felületekből (pl. henger, kúp, ellipszoid stb.) álló lábak, test, nyak, fej, szemek, csőr, illetve tetszőlegesen megoldható taraj és farok. A fej a nyakon forgatható, a lábak a csípőben, térben és a lábfejben előre/hátra forgathatók, a térd csirkelábként viselkedik, azaz előre hajlik. A csirke az út szélén várja sorsának beteljesülését.
- Úthenger: Diffúz/spekuláris fémes csillogású, poliéderekből (pl. téglatest, extrúdált poligon) összerakott karosszériából és textúrázott hengerekből áll. Bónusz: az úthenger kéményén átlátszó, szétfoszló füstcsomókat ereget. Az úthenger az úton áll, felkészülvén a hengerelésre.
- Füves, lapos, zöld, diffúz terep, amelyen egy textúrázott aszfalt út vezet át.
A virtuális világot egy irányfényforrás (a Nap) világítja meg, a csirke és az úthenger a terepre és az útra koromfekete árnyékot vetnek. Ambiens fény van, de az sem világosítja fel az árnyékokat.
A virtuális kamerával külső szemlélőként követjük az eseményeket.
A textúrák kizárólag procedurálisan generálhatók, óriási, konstansokkal inicializált tömbök használata tilos.
Virtuális kamerával külső szemlélőként követjük az eseményeket.
Beadási határidő: 2011. 11. 28. 23:59
Ötödik feladat
A 4. feladatból készítsen játékot két játékos számára, az egyik a csirkéket irányítja, a másik az úthengert.
Három csirke van, amelyek az út szélén várakoznak, és Játékos I. a 'c' billentyű lenyomására indíthatja őket egyesével. Az elindított csirke átsétál az úttesten, és ha túlélte boldogan ácsorog a túloldalon. A sétálás közben a támaszkodó láb nem csúszkál (inverz kinematika), a test az ízületekben nem szakad szét (karakteranimáció). Ha az úthenger eltapossa (ütközésdetektálás), a csirke kilapítottan az aszfalton marad örök mementóként (ütközésválasz).
Játékos II. az úthengert irányítja. Az 'f' billentyűvel az úthengert az orra irányába konstans gyorsulásra bírhatja, a 'b' hatására hátrafelé hasonló nagyságú gyorsulást állíthat be, az 'n' hatására a gyorsulás zérus (fizikai animáció: a sebesség és a pillanatnyi hely a dinamika alaptörvényéből számítandó).
A játékban három kamera van, az egyik a csirkék kiindulási helye körül köröz, a második a soron következő, fejét jobbra-balra forgató csirke szemszögéből mutatja be a színteret, a harmadik pedig az úthenger pilótafülkéjéből (a sebességvektor irányában). A három kamera képét három nézetben (viewport) kell megjeleníteni az alkalmazói ablakban.
A fényforrás napként viselkedik, 10 másodperces periódusidővel vöröses árnyalattal felkel, fehéren delel, majd vörösesen nyugovóra tér (fényanimáció).
Az "inverz kinematika", "fizikai animáció", "ütközés válasz", "több kamerás/nézetes képszintézis" és "fényanimáció" részfeladatokból 2 szükség esetén elhagyható.
Beadási határidő: 2011. 12. 11. 23:59
2010/11 tavaszi félév
A mintaképek csak illusztrációk, legtöbbször nem futó OpenGL programból, hanem egyéb módon lettek elkészítve!
Első feladat
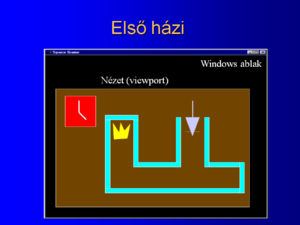
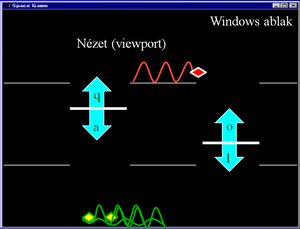
Egér labirintusban.
A szürke kisegér (háromszög alakú test, vonal farok) három billentyűvel irányítható (e=előre, j=jobbra, b=balra, mindig az egér orrához képest). Előrelépésnél a lépéshossz állandó, amit az egér egyenes vonalú egyenletes mozgással 1 sec alatt tesz meg. A fordulás 90 fokos és pillanatszerű.
Amennyiben az előrelépésnél a falon átmenne az egér, a teljes ablak piros színnel felvillan 2 másodpercig, és az egér nem mozdul el a kiindulási állapottól. A labirintus falai tetszés szerint téglalapok vagy vonalak. A labirintus végében egy sokszög alakú sárga sajt van.
A képen egy másodperc és perc mutatóval ellátott, járó óra is látható, amely akkor áll meg, ha az egér eléri a sajtot.
Második feladat
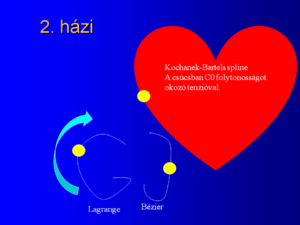
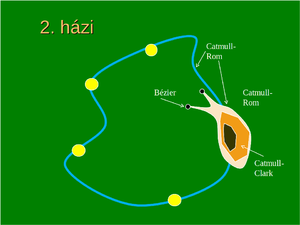
Készítsen Valentin napi dobogó szívecskét!
A virtuális világunk 20cm x 20cm-es négyzetben képzelendő el, amelyben a saját monogramja és egy dobogó szív látható. A háttér szín kék, a monogram fehér, a szív kitöltési színe (nyilván) piros. A vezetéknév Lagrange interpolációs görbe, a keresztnév Bézier görbe, a szív határa Kochanek-Bartels spline. A szívben a tenzió (tension) értéket úgy kell vezérelni, hogy a szív alja és a felső völgyének alja is hegyes legyen (Találós kérdés: miért így ábrázolja az emberiség a szívet?).
A szív az alsó csücskét helyben tartva dobog, másodpercenként egyet ver eredeti lineáris méreteit 50 %-kal megnövelve, a két szélső állapota között folyamatosan mozogva. A görbéken és a szív határán egy-egy kitöltött sárga körlap szalad végig, mégpedig úgy, hogy 2 másodperc alatt tegye meg a teljes görbét. A körlap a pálya végén elindul visszafelé. A kameraablak 18cm x 15cm méretű.
Megjegyzés: A feladatkiadáskor az előadáson elhangzottak is a specifikáció elidegeníthetetlen részét képezik. Uff.
Harmadik feladat
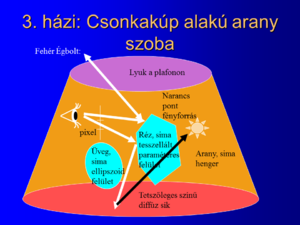
Üveg ellipszoid és rézből készült tesszellált, paraméteres felület arany falú csonkakúpban, sugárkövetéssel megjelenítve.
A csonkakúp alja diffúz, a teteje hiányzik. A tetőn keresztül az ég látszik, amelynek intenzitása minden hullámhosszon azonos.
A réz objektumot egy tetszőleges parametrikus felületből kell származtatni tesszellációval, azaz a felület háromszöghálóval történő közelítésével. A háromszögek száma max. 100 lehet.
A csonkakúp belsejében van a virtuális kamera és egy narancs színű pontfényforrás.
A kamerát úgy kell beállítani, hogy az üveg és a réz tárgyak teljes szépségükben pompázzanak. A diffúz felületen a lokális illuminációs modell értelmében csak a pontfényforrás hatása érvényesülhet.
Törésmutató/kioldási tényező a g,b,r hullámhosszokon:
b b g r Üveg (n/k) 1.5/0 1.5/0 1.5/0 Arany (n/k) 1.5/1.9 0.35/2.7 0.17/3.1 Réz (n/k) 1.2/2.3 1.1/2.6 0.2/3.6
A törésmutató egynél kisebb értéket is felvesz, azaz ezek szerint az anyag belsejében a fény 300000 km/sec-nél is gyorsabban halad (nincs itt ellentmondás?).
Az algoritmust a CPU-ra kell implementálni, a kiszámított képet glDrawPixels(width, height, format, type, data) hívással kell a rasztertárba másolni.
A program nem tartalmazhat felesleges utasításokat
Negyedik feladat
Készítsen 3D színteret és jelenítse meg OpenGL-lel.
A színtérben egy textúrázott, megvilágított ember látható (fej, nyak, test, comb, alsó lábszár, felkar, alkar, amelyeket saját programmal tesszellált kvadratikus felületekből lehet összerakni), valamint egy fényes, fémes kard poligonmodellel leírva, textúrázott föld és tetszőlegesen kialakítható textúrázott és megvilágítható tereptárgyak.
Az ember a bal és jobb kezében egy-egy pontfényforrást tart, a teret még a nap, mint irányfényforrás és az ég, mint ambiens forrás világítja meg.
A kard orientációja kvaternióval adandó meg.
Miként korábban, továbbra is érvényes, hogy csak az idáig tanult és a fejlécben szereplő függvények alkalmazhatók, tehát a glu Quadric családja (pl. gluSphere) NEM. Kéretik a textúrákat procedurálisan generálni, kilométeres inicializált tömbök mellőzendők.
2010/11 Őszi félév
A mintaképek csak illusztrációk, legtöbbször nem futó OpenGL programból, hanem egyéb módon lettek elkészítve!
Első feladat
Írjon 2D útkereszteződés szimulátort. A zebra fekete fehér, a járókelők színes téglalapok, az autók ugyancsak. A járókelőknek zöld/piros lámpájuk van, az autóknak piros/sárga/zöld, amelyek a szokásos működésűek és ugyancsak téglalap alakúak. Az autók lámpája 5 másodpercig zöld, 4 másodpercig sárga és 5 másodpercig piros, a gyalogosoké szinkronban működik.
Az autók automatikusan közlekednek és mindig tiszteletben tartják a lámpa utasításait, azaz piros lámpa esetén mindig megállnak éppen ott ahol vannak (nem kell előrecsorogni a lámpáig). A járókelőt viszont tetszőleges időpontban elindíthatjuk úgy, hogy az egér bal gombját lenyomjuk, amikor a kurzor éppen felette van. Ha az autó elüti a járókelőnket, akkor az eltűnik. Egy SPACE lenyomása után kapunk új járókelőt, aki a képernyő jobb szélén ütközve, függőleges irányban pedig a képernyő közepén jelenik meg. A SPACE hatására nem csak egy új járókelő születik a zebra szélén, hanem a képszintézis nézete (viewport) megváltozik, mind méretében, mind pedig a windows ablakon belüli helyében. A járókelő 5 másodperc alatt ér át az úton. Mialatt a gyalogosnak piros a jelzés, az autók folyamatosan jönnek és 3 másodperc alatt mennek át a kameránk látóterén.
A program futásának kezdetén a viewport legyen a teljes 600x600 pixel nagyságú ablak!
A feladat megoldásához csak azok az OpenGL függvények használhatók, amelyek az első két héten előkerültek.
Beadási határidő: 2010. 09. 30. 23:59
Második feladat
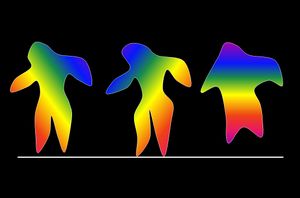
A Placcs családban három lány van, Placcs Bereniké, Placcs Cezarina és Placcs Nikodémia. Benediké 2D-s sziluettjét egyetlen Bézier görbével, Cezariáét egy Catmull-Rom spline-nal, Nikodémiáét pedig egy NURBS-szel írhatjuk le (vajon melyikük schlank?).
A lányok normális testalkatúak, tehát egy-egy fejük, két-két lábuk, illetve kezük van. A lányokat hasonló referenciahelyzetben, célszerűen, de nem kötelezően, ugyanazokkal a vezérlőpontokkal definiáljuk. A Placcs család a 2D-s világban egy 10 m hosszú és 10 méter magas lakást birtokol, a kb. 3 méter magas lányok a világban kényelmesen elférnek egymás mellett. A lányok balettoznak, így ha nevük kezdőbetűjét lenyomjuk, akkor egy 1 méter magas grand jeté-t mutatnak be (= nagy, repülésszerű ugrás, horizontálisan szétvetett lábakkal) és a levegőben maradnak mindaddig, amíg rájuk nem klikkelünk. Ekkor visszatérnek a földre (a lányok lába a föld közelébe kerül, de nem kell tökéletesen pontosan a földön állniuk). A lányokat szivárvány színátmenettel kitöltött területekkel jelenítjük meg, ahol monokromatikus fényeknek megfelelő színek követik egymást, minden lánynál más irányban.

A 2D kamera (ablak), amelyen keresztül belesünk Placcsék lakásába, kezdetben a teljes szobát mutatja. A középső lány olyan magasra fog ugrani, hogy a kamerakép közepére kerüljön. SPACE lenyomására a kameránk mindig a következő lányt veszi célba (a lány, ha felugrott a kép közepén lesz), és a kamerán "látószöge" (a befogott tartomány) minden SPACE után kisebb lesz, azaz folyamatosan zoom-olunk. A referenciahelyzetből a világ aktuális helyére vivő modellezési transzformációt az OpenGL MODELVIEW, a kameratranszformációt pedig a PROJECTION transzformációjával kell megvalósítani.
A megoldásban csak a "2D grafikus rendszerek" végéig tanult OpenGL függvények alkalmazhatók (pl. textúrák nem). A GL_POLYGON nem robusztus és ezért nem megengedett, a glu tesszellátorok tiltottak, mert nem tanuljuk őket. A beadott programban a memória nem szivároghat, azaz a dinamikus allokációt a lehetőség szerint mellőzzék (lélekben is C++-ban programozzanak), ha mégis erre kényszerülnek, akkor pedig szabadítsák fel a feleslegessé vált memóriaterületeket.
Színillesztő függvényeket elég durván közelíteni. Egy túlságosan finom mintavételezésű változat az alábbi honlapon elérhető: http://cvision.ucsd.edu/cmfs.htm
Beadási határidő: 2010. 10. 30. 23:59
Harmadik feladat
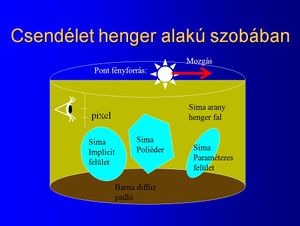
Készítsen mozgó pont fényforrással megvilágított csendéletet kétirányú sugárkövetéssel.
A sugárkövetést a CPU-n kell megvalósítani, a kiszámított és tone-mappelt 600x600 felbontású képet glDrawPixels hívással kell a rasztertárba írni.
A színtér egy henger alakú szoba, amelynek fala optikailag sima arany, padlója barna diffúz felület. A szobában három optikailag sima felületű tárgy van, egy poliéder, egy parametrikus felületből tesszellált háromszögháló és egy implicit felület, amelyek közül az egyik üveg, a másik réz, a harmadik pedig ezüst. A tárgyak primitívszáma (háromszögek és kvadratikus felületek száma) max. 100 lehet. A szobát egy izotróp (irányfüggetlen) fehér fényforrás világítja meg, amely 10 másodperc alatt faltól falig vándorol. A fotonlövés fázisában, a beadott változatban ne indítsunk túl sok fotont (pl. max tízezer), azaz a képszintézis ideje az 1 percet ne lépje túl. A diffúz anyagú padlóhoz rendelt fotontérkép felbontása 100x100.
Poliéder példák: http://local.wasp.uwa.edu.au/~pbourke/geometry/platonic/
Paraméteres felület példák: http://www.vtk.org/VTK/img/ParametricSurfaces.pdf
Anyagmodellek: az n törésmutató/ k kioltási tényező 440 nm-en (kék), 520 nm-en (zöld) és 650 nm-en (piros).
Üveg (n/k): 1.5/0, 1.5/0 1.5/0 Arany (n/k): 1.5/1.9 0.35/2.7 0.17/3.1 Ezüst (n/k): 0.16/2.3 0.13/3.1 0.14/4.1 Réz (n/k): 1.2/2.3 1.1/2.6 0.2/3.6
Beadási határidő: 2010. 11. 10. 23:59
Kiadás dátuma: 2010. 10. 19.
Negyedik feladat
Írjon OpenGL programot, amely a Star Wars univerzum Rishi bolygóján egy rövid jelenetet mutat be.
A talaj sík, diffúz textúzott. A talajon két db. kétlábú, spekuláris fémes jellegű All Terrain Empire Walker (ATEW) áll, amelyek a csípő és a térdízületeiket mozgathatják, ezen kívül a felső részük elfordulhat, a felső részükhöz rögzített ágyúcső emelkedési szöge állítható. A Rishi-nek három Napja van, amelyek irányfényforrások, az ATEW-ek lövedékei gömbök, amelyek pontfényforrásokként is működnek. Az ég ambiens fényforrás. Az ATEW-eken kívül még néhány szabadon megválasztható textúrázott tereptárgy is található.
A virtuális kamera a jelenet körül kering, vigyázó tekintetét a két ATEW középpontjára veti.
Beadási határidő: 2010. 11. 28. 23:59
Ötödik feladat
A 4. feladatban szereplő ATEW-eket sétáljanak és harcoljanak. Az ATEW-ek folyamatosan előre lépdelnek, kétmásodpercenként egyet lépve. A támaszkodó láb mindig nyújtva van (térdízület merev), az emelt lábon viszont a térd hajlít. A támaszkodó láb nem csúszkál a földön (inverz kinematika). Az ATEW-ek megpróbálják egymást lelőni. A lövedék ferde hajítással lassan repül, a (sebességgel arányos) közegellenállás jelentős és pontról-pontra véletlenszerűen változik a levegőben, hogy nehezebben találják el egymást. Az eltalált (elég a befoglaló térfogat eltalálását ellenőrizni) ATEW hanyatt esik.
A textúrákat procedurálisan kell generálni, a textúrázott felületeken is hat az illumináció. Az avatárunk a jelenet körül forog, tekintetét az ATEW-ek közé veti.
A szimuláció során használt időlépést kisebbre lehet venni, mint az Idle időlépését, azaz, ha az Idle-ban kapott időváltozás túl nagy, azt több szimulációs lépéssel is fel lehet dolgozni (a szimulációs időlépés lehet pl. 0.1 sec).
Beadási határidő: 2010. 12. 13. 23:59
Válogatás a 2010. évi kisházi feladatokból:
3. kisházi:
Angeli Róbert, Koczka Tamás, Leitner Szabolcs, Kovács Balázs, Zsemlye Nóra
5. kisházi:
Gulyás Máté, Kovács Andor, Kántor Tibor, Rajcsányi Vilmos, Balogh Norbert, Keresztes Ádám, Tükör Gábor, Mészáros Kornél, Illés János, Szebeni Szilveszter, Baski Attila, Koczka Tamás, Bozóki Szilárd, Medvey Ádám, Dul Dávid, Leitner Szabolcs, Szabó Péter, Pusztai Bálint, Dorjgotov Anudar, Lám István, Angeli Róbert, Viniczay Dávid, Schmidt Antonio, Szabó Péter, Diószegi Tamás, Fekete András, Hámos Gergely, Nagy Zoltán Adrián, Csontos Gábor, Szabó András, Kiss Attila, Szabó Bálint István, Kovács Dávid Balázs, Lázár Endre, Vőneki Balázs, Magyar Ferenc, Bori András, Lenthár Gábor, Kávássy Dániel, Mikó Norbert
2009/10 Őszi félév
Első feladat
Írjon egyenletes B-spline rajzoló programot OpenGL felhasználásával. A vezérlőpontokat egy globális tömbben tárolja, a vezérlőpontok száma min 10, max 100 lehet. A program indulásakor a vezérlőpontok látszanak a képernyőn, a görbe, valamint a görbe deriváltját (sebesség) és második deriváltját (gyorsulás) jelképező vektorok a t=0 paraméterértéknél. A vektorokat nyilakkal kell ábrázolni. Az egyes elemek színe eltérő. Minden SPACE billentyű lenyomásra, a t paraméter 0.3-mal nő, amelynél a görbe pontja, a sebesség és gyorsulás vektorok felrajzolandók. Ha elértük a görbe végét, akkor a folyamat kezdődik előlről. Az nézeti téglalap a teljes ablakot lefedi és felbontása 600x600. Fontos figyelmeztetések: 1. A feladat szövegében derivált, azaz differenciálhányados szerepel, nem pedig annak differenciahányadossal történő közelítése. A deriváltat analitikusan kell kiszámolni. 2. Más által írt program kiherélt változata, ami nem tartalmaz jelentős saját hozzájárulást = PLÁGIUM. 3. glut függvényeket használni tilos. 4. glu függvényeket csak akkor lehet használni, ha a feladat szövege ezt kifejezetten engedélyezi. Az első feladat esetében pl. a gluOrtho2D nem használható.
Beadási határidő: 2009. 10. 20. 23:60
- Egy feladatmegoldás (Nagy Máté)
- Egy másik feladatmegoldás (Mikeol)
- Egy harmadik feladatmegoldás (obrien)
Második feladat
A kecskeméti új Mercedes gyár Önt kérte fel, hogy az új XXX kategóriás csúcsmodelljében a fényszórót tervezze meg. A fényforrás pontszerű, izotróp (azaz kibocsátott fotonok iránya egyenletes eloszlású), fénye fehér. A forrást körülvevő fényvető búra paraboloid, amely aranyból van, mert az XXX kategóriánál így dukál. A lámpából a fény egy ellipszoid alakú lencsén keresztül lép ki (lásd a csatolt ábrát).
Az arany és az üveg törésmutatója, valamint kioltási tényezője a kék, zöld és vörös fény hullámhosszain a következő:
Arany törésmutató: 1.5 0.35 0.17 Arany kioltási tényező: 1.9 2.7 3.1 Üveg törésmutató: 1.5 1.5 1.5 Üveg kioltási tényező: 0 0 0
Egy szimulátorprogramot kell készítenie, amely a lámpa előtt lévő függőleges falon egy alkalmas négyzet belsejében megjelenő képet kiszámítja és a képernyőn megjeleníti. A képernyőn a falnak a lámpa által bevilágított négyzete tűnik fel, 600x600-as felbontásban, ahol egy pixel vörös/zöld/kék intenzitása a pixelnek megfelelő felületdarabra eső teljesítménnyel arányos a megfelelő hullámhosszon. Az arányossági tényezőt úgy kell beállítani, hogy a pixelek színintenzitásai a 0-1 tartományba essenek. Az első képet tízezer, egyenletes eloszlású véletlen kezdeti iránnyal létrehozott foton követésével állítsa elő. Minden space billentyű hatására a fotonok számát növelje az előző érték tízszeresére. A nem specifikált méreteket úgy vegye fel, hogy szép kép szülessen. A visszaverődés valószínűségét a Fresnel egyenlet alapján számítsa, a törési irányt pedig a Snellius-Descartes törvény szerint. A foton utakat csak maximum 5 szóródásig kell követni.
A számításokat a CPU-n végezze el, az OpenGL-t csak az elkészült kép megjelenítésére használja. Az OpenGL egy képet a glDrawPixels függvény hatására tesz ki.
Segítség az egyenletes eloszlású irányok létrehozása: Három egymás utáni, egyenletes eloszlású véletlen számot skálázzunk át a [-1,1] intervallumra. A számokat egy pont koordinátáinak tekintve a (-1,-1,-1), (1,1,1) sarokpontú kockában egyenletes eloszlással generálunk pontokat. Ha a pont az origó középpontú egységsugarú gömbön kívül van, a mintát elvetjük. A megmaradó pontok a gömb belsejében egyenletes eloszlásúak lesznek, azaz ha őket a gömb felületére vetítjük (normalizálás), akkor az egységsugarú gömb felületét – azaz az irányok halmazát – mintavételezzük egyenletesen.
Beadási határidő: 2009. 11. 03. 23:59
Harmadik feladat
Előzetes kiírás.
Hozzon létre egy virtuális világot és jelenítse meg OpenGL-lel (Cg nem használható). A virtuális világ egy 1 négyzetkilométer földterület,ahol NxM piramis (N,M>4) és egy tank található. A föld zöld, diffúz, a piramisok sárgás-fehérek és spekulárisan csillogóak, a tankon terepszínű textúra látható és ugyancsak csillogó. A nap keletről süt, 20 fokot zár be a talajjal. A nap erős intenzitású fehér irányfényforrásnak tekinthető. Az égbolt (ambiens) fény sugársűrűsége konstans, türkiszkék (szép idő van).
A tank teste poligonokból áll, lövegtornya hengerszerű, az ágyú ugyancsak henger, amelynek a belseje üres, különben nem tudna lőni. A lövegtorony forgatható, az ágyú emelhető. A lánctalpak részletes kidolgozása mellőzhető (de nem tiltott). A tank lőtt, és most éppen a lövedék a cső végének közelében van. A lövedék hengerszimmetrikus, csúcsa hegyes, szürke, csillogó. A jobb láthatóság miatt a lövedék sugara lehet nagyobb mint az ágyucső sugara.
A piramisok és a tank földre vetített árnyékát nem kötelező megjeleníteni (de lehet). Állítsa be a virtuális kamerát úgy, hogy a tank, a repülő lövedék és a piramisok egy része látható legyen.
Beadási határidő: 2009. 11. 15. 23:5
Negyedik feladat
A harmadik feladat ellenséges tankját pályaanimációval mozgassa a [0,5] sec időintervallumon egy Bézier görbe mentén. A lövegtorony mindig az avatár felé fordul, a löveg emelkedik úgy, hogy a ferde hajítás éppen az avatárnál fejeződjön be. A t=1 sec pillanatban a tank lő, a golyó ferde hajítással elrepül. Az avatár szintén egy tank, de csak a környezetet látja (FPS). Az avatártank két botkormánnyal vezérelhető, amelyek a bal és jobb lánctalpakhoz vannak kötve. A botkormányokat q, illetve p billentyűkkel lehet előre dönteni (a botkormányok alaphelyzetbe állításához bármilyen megoldást kitalálhat, azt úgy sem fogjuk tesztelni). Az avatártank a piramisokon nem hatolhat át. Az időlekérdezéshez a glutGet(GLUT_ELAPSED_TIME) függvény használható.
Beadási határidő: 2009. 12. 10. 23:59
Nagy házi feladatok tabló

