Algoritmuselmélet 2010.11.19. PZH megoldásai

← Vissza az előző oldalra – Algoritmuselmélet

2010.11.19 - PZH megoldásai

1. Feladat (Van megoldás)

Az alábbi függvényeket rendezze olyan sorozatba, hogy ha $f_i$ után közvetlenül $f_j$ következik a sorban, akkor $f_i(n)=O(f_j(n))$ teljesüljün!

• $f_1(n)=2010\cdot lo{g}_3(n^n)$
  
  
• $f_2(n)=n^{1+2+\dots +loglogn}$
  
  
• $f_3(n)=4^{100+logn}$
  
  

Megoldás

• $f_1(n)=2010\cdot lo{g}_3(n^n)=2010n\cdot lo{g}_{3}n$
  
  
• $f_2(n)=n^{1+2+\dots +loglogn}$ ezt alulról becsülhetjük $f_2^{*}(n)=n^{logn}$-nel.
  
  
• $f_3(n)=4^{100+logn}=4^{100}\cdot 4^{logn}=4^{100}\cdot (2^2{)}^{logn}=4^{100}\cdot (2^{logn}{)}^2=4^{100}\cdot n^2$
  
  

• Első lépésben belátjuk, hogy $f_1(n)=O(f_3(n)).$
  
  
  • $2010n\cdot lo{g}_{3}n\le c\cdot 4^{100}\cdot n^2$
    
    
  • $2010\cdot lo{g}_{3}n\le c\cdot 4^{100}\cdot n$
    
    
  • $lo{g}_{3}n\le c\cdot \frac{4^{100}}{2010}\cdot n$
    
    
  • $c=\frac{2010}{4^{100}},n\ge 1$
    
    

• Második lépésben belátjuk, hogy $f_1(n)=O(f_2^{*}(n)).$ (Ha ezt belátjuk, akkor $f_1(n)=O(f_2(n))$ is igaz lesz.)
  
  
  • $4^{100}\cdot n^2\le c\cdot n^{logn}$
    
    
  • $n^2\le \frac{c}{4^{100}}\cdot n^{logn}$
    
    
  • $c=4^{100}$
    
    
  • És a kitevők alapján pedig $n\ge 4$
    
    

• Tehát a megoldás $f_1(n)\to f_3(n)\to f_2(n).$

2. Feladat

TODO

Megoldás

TODO

3. Feladat

TODO

Megoldás

TODO

4. Feladat (Van megoldás)

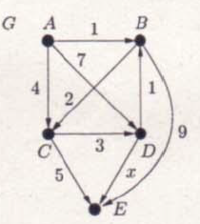
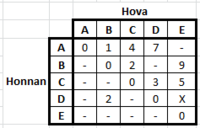
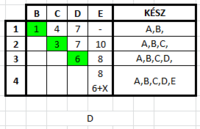
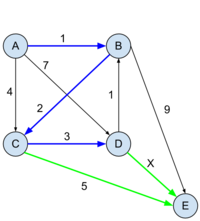
Dijkstra algoritmussal határozza meg a G gráfban az $A$ pontból az összes többi pontba menő legrövidebb utak hosszát az $X$ pozitív valós paraméter függvényében. Minden lépésnél írja fel a távolságokat tartalmazó D tömb állapotát, és a KÉSZ halmaz elemeit.

Megoldás

• Egy egyszerű Dijkstra-s feladat.
• Annyit kell megjegyezni hozzá, hogy:
  • Ha $X\le 2$, akkor az $X$ élt $(D\to E)$ veszi be.
  • Ha $X\ge 2$, akkor a $C\to E$ élt veszi be.

5. Feladat

TODO

Megoldás

TODO

6. Feladat (Van megoldás)

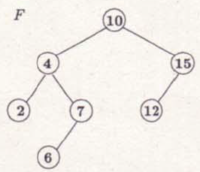
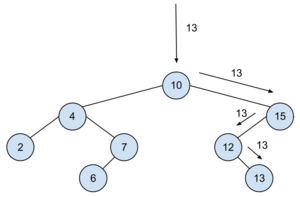
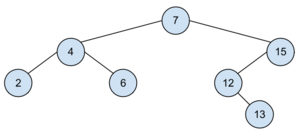
Hajtsa végre az alábbi $F$ bináris keresőfán a BESZÚR(13), TÖRÖL(10) műveleteket! Minden lépést jelezzen!

Megoldás

• BESZÚR(13):
  • Egyszerű, mint az 1x1
    

• TÖRÖL(10):
  • Töröljük a 10-t.
  • A BAL oldali részfából kiválasztjuk a LEGNAGYOBB elemet, és berakjuk a gyökérbe (ebben az esetben a 7).
  • A fát rendbe rakjuk (ez esetben a 6-t beírjuk a 7 régi helyére).
    

7. Feladat (Van megoldás)

Egy piros-fekete fa gyökerének mindkét gyereke fekete. A gyökér baloldali részfájában 14, a jobboldali részfájában 63 elemet tárolunk. Mennyi lehet a fa fekete-magassága?

Megoldás

• Először vizsgáljuk a jobboldali részfát:
  • Tudjuk, hogy $n\le 2^m-1\Rightarrow 63\le 2^m-1\Rightarrow m\ge 6$, vagyis a jobb oldali részfa magassága legalább 6.
    
    
  • Továbbá $fm\ge \frac{m}{2}\Rightarrow fm\ge 3$
    
    
• Most nézzük a baloldali részfát:
  • Ismert, hogy $b_v\ge 2^{fm(v)}-1\Rightarrow 14\ge 2^{fm(v)}-1\Rightarrow fm\le 3.907\Rightarrow \Rightarrow fm<4$

• A 2 korlátot összevetve jön ki, hogy a bal és jobb részfa esetén $fm=3.$
• Emiatt az eredeti fában pedig $fm=4.$

8. Feladat

TODO

Megoldás

TODO