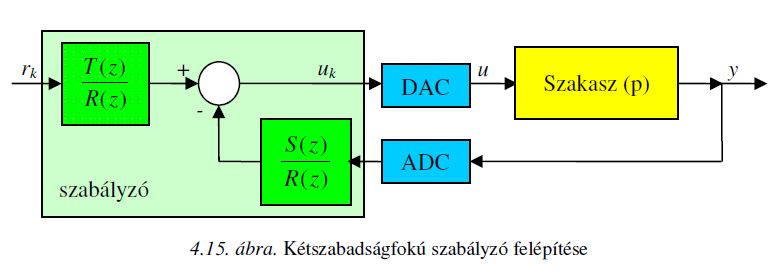
Szabályozástechnika - 2DOF szabályzó tervezése
A VIK Wikiből
A szakasz megadása és a zárt körre vonatkozó előírások
%% A szakasz a szokásos:
% Aplant
% Wp(s) = ---------------------
% (1+sT1)(1+sT2)(1+sT3)
Aplant=5;
T1=10;
T2=4;
T3=1;
wp=tf(Aplant,conv(conv([T1 1],[T2 1]),[T3 1]))
%% A zárt körre vonatkozó előírások
xi=0.7; % A domináns póluspár csillapítása
w0=1/3; % A domináns póluspár sajátfrekvenciája
scinf=-1; % További pólusok (ha szükséges)
soinf=-5; % Megfigyelő pólusok
lint=1; % Zárt körbe veendő integrátorok száma
%% A zárt kör domináns póluspárjának számítása
sdom1=-w0*xi+j*w0*sqrt(1-xi^2)
sdom2=conj(sdom1)
%% Áttérés diszkrét időre
Ts=0.2; % Mintavételi idő [s]
dp=c2d(wp,Ts,'zoh') % Áttérés diszkrét időre nulladrendű tartószervet feltételezve
zdom1=exp(sdom1*Ts) % Áttérés a z=exp(s*Ts) képlet szerint
zdom2=exp(sdom2*Ts)
zcinf=exp(scinf*Ts)
zoinf=exp(soinf*Ts)
A megoldandó egyenlet levezetése
% A 2DOF szabályzó tervezés alapelve, hogy mi a zárt kör átviteli függvényében
% előre meghatározott pólusokat szeretnénk. Azaz célunk, hogy:
%
% Bm Ao
% Dcl = ---- * ---- alakú legyen, ahol Ao az úgynevezett observer polinom.
% Am Ao
%
% Am gyökei az általunk előírt pólusok - zdom1, zdom2 és ha szükséges akkor megfelelő számú zcinf pólus is.
% Ao gyökei pedig (csak ha szükséges) - megfelelő számú zoinf pólus.
% A szakasz diszkrétidejű átviteli függvénye: D(z) = B(z) / A(z)
% A zárt kör átviteli függvénye:
%
% T B/A T*B Bm Ao
% Dcl = --- * --------------- = ----------- == ---- * ----
% R 1 + B/A * S/R A*R + B*S Am Ao
%
% Szeretnénk egyszerűsíteni a B polinommal, így R gyökei közé bevesszük B gyökeit.
% Azonban R gyökei közé csak a B stabilis gyökeit tehetjük, a szabályzó stabilitásának érdekében.
% Így B = Bplus * Bminus felbontásra jutunk, ahol Bplus tartalmazza B kiejthető gyökeit,
% azaz azokat, amelyek az egységkörön belül vannak és NEM tisztán negatív valósak!
% Tehát R gyökei közé bevehetjük Bplus gyökeit: R = R1 * Bplus
% Így le tudunk egyszerűsíteni Bplus-al az egyenlet bal oldalán:
%
% T*Bminus Bm Ao
% ----------------- == ---- * ----
% A*R1 + Bminus*S Am Ao
%
% Az egyenletből látszik, hogy Bm polinomnak mindenképpen tartalmaznia kell B nem kiejthető gyökeit,
% azaz Bm = Bm' * Bminus alakú kell hogy legyen. Így tovább egyszerűsíthetünk:
%
% T Bm' Ao
% ----------------- == ---- * ----
% A*R1 + Bminus*S Am Ao
%
% Előírás lehet, hogy a szabályzó "k" darab integrátort tartalmazzon, melyeket az R polinomba
% kell bepakolnunk. Azaz R = R1 * Bplus, ahol R1 = (z-1)^k * R1'
% Így a végleges egyenletünk:
%
% T Bm' Ao
% -------------------------- == ---- * ----
% A*(z-1)^k*R1' + Bminus*S Am Ao
%
% Ez alapján a szabályzó T polinomja egyszerűen számítható: T = Bm' * Ao
% Az egyenlet nevezője pedig egy diophantoszi polinomegyenlet, amiből a lentebb ismertetett
% módszerrel R1' (ebből pedig R) és S már egyszerűen meghatározható.
A számláló faktorizálása
B=dp.num{1} % Számláló kiolvasása a tf struktúrából
A=dp.den{1}; % Nevező kiolvasása a tf struktúrából
% Mivel a polinomok fokszámait majd az őket tároló vektorok hosszából számítjuk
% (fokszám = vektor elemszáma - 1), a Matlab pedig az átviteli függvény számlálóját
% és nevezőjét egyforma elemszámú vektorokban tárolja, ezért B elejéről le kell
% választanunk a vezető 0 elemeket.
% Jelen esetben csak 1 darab van, így csak azt kell levágni.
B=B(2:end)
Bpoles=roots(B) % B gyökeinek számítása
% Kiejthető gyökök: Egységkörön belül és NEM tisztán negatív valósak
% Nem kiejthető gyökök: Egységkörön kívűl, vagy tisztán negatív valósak
Bminus=B % Esetünkben egyik zérus sem kiejthető, mivel mind negatív valósak
Bplus=1 % FONTOS: Ha Bplus polinom nem egy konstans 1-es, akkor mindig meg kell szorozni B(1)-el!
% Általánosan kis manuális beavatkozással:
% roots(B)
% Megnézzük, hogy mik a kiejthető és mik a ki nem ejthető gyökök
% Bplus=poly([ kiejthető gyökök felsorolása ])
% Bminus=B(1)*poly([ nem kiejthető gyökök felsorolása ])
% -------------------------------------------------------------------------------------------------------
%% Csak ÍNYENCEKNEK - általános megoldás a Matlab lehetőségeit kihasználva.
% Bminus-ba azok a gyökök kerülnek, amiknek az abszolútértéke >=1 illetve tisztán valósak és negatívak.
% Az & jel a két feltétel közötti ÉS kapcsolatot jelenti, az union két halmaz (esetünkben vektor) uniója.
% Ezt a műveletet használva minden olyan elem bekerül Bminuspoles-ba, amelyre valamelyik feltétel igaz,
% de akkor is csak egyszer fog szerepelni, ha mindkét feltétel igaz rá.
Bminuspoles=union(Bpoles(abs(Bpoles)>=1), Bpoles((real(Bpoles)<0)&(imag(Bpoles)<1e-12)));
% Bplus-ba Bpoles es Bminuspoles különbsége kerül
Bpluspoles=setdiff(Bpoles,Bminuspoles);
% Bplus polinom összeállítása a gyökökből
Bplus=poly(Bpluspoles);
% Hogy Bplus*Bminus=B legyen, Bminus-t még szorozni kell egy megfelelő konstanssal, hiszen a poly
% mindenképpen 1 vezető együtthatójú polinomot képez az elemekből és az elmélet szerint Bplus monic.
Bminus=poly(Bminuspoles)*B(1);
Fokszámfeltételek (Tk - 240. oldal)
% A fokszámokat a vizsgán általában egyszerűbb és gyorsabb kézzel kiszámítani
% az ismert képletek használatával, de számíthatóak általánosan Matlab segítségével is.
grBminus=length(Bminus)-1 % A vezető 0-t már korábban leválasztottuk
grA=length(A)-1
% grAm=1+grBminus+{1: grBminus=0; 0 egyébként} - grAm legalább másodfokú kell legyen!
% grAo=grA+lint-1-{1: grBminus=0; 0 egyébként}
% Itt grBminus=2, így jelen esetben NEM kell hozzáadnunk illetve levonnunk semmit.
grAm=1+grBminus
grAo=grA+lint-1
grS=grA+lint-1
grR1prime=grBminus
% Általános megoldás - csak ínyenceknek!
% grBminus==0 1-re értékelődik ki ha Bminus fokszáma 0, 0-ra egyébként
% grAm=1+grBminus+(grBminus==0);
% grAo=grA+lint-1-(grBminus==0);
%% Referencia- és megfigyelő polinom számítása
% A polinomokat a gyökeikből a poly függvény segítségével számítjuk. Fontos, hogy a poly 1 vezető
% együtthatójú (monic) polinomokat képez, és az elmélet szerint Am és Ao is monic. Am harmadfokú (grAm=3),
% így a domináns póluspár mellett grAm-2, azaz egyszeres multiplicitással kell a zcinf pólust szerepeltetni
Am=poly([zdom1 zdom2 zcinf])
% Ao egyetlen gyöke zoinf, ezt kell most grAo, azaz háromszoros multiplicitással szerepeltetni
Ao=poly([zoinf zoinf zoinf])
% Általános megoldás:
% Am=poly([zdom1 zdom2 ones(1,grAm-2)*zcinf])
% Ao=poly(ones(1,grAo)*zoinf)
% B'm számítása: Szeretnénk, ha a zárt körnek egységugrás alapjel esetén zérus maradó hibája lenne,
% azaz a zárt kör ugrásválaszának végértéke 1 lenne:
% lim (z -> 1) { (1-z^-1)*Dcl(z)*1/(1-z^-1) } = lim (z -> 1 ) { Dcl(z) } = Dcl(1)
% 1 = Dcl(1) = Bm(1)/Am(1) = Bminus(1) * Bm' / Am(1) --> B'm = Am(z=1) / Bminus(z=1)
Bmprime=polyval(Am,1)/polyval(Bminus,1)
A diophantoszi polinomegyenlet megoldása
polyint=[1 -1]; % Az integrátor polinomja (z-1)
% Általános megoldás - csak ínyenceknek!
% lint számú integrátorra a polyint polinom számítása ( (z-1)^lint )
polyint=1;
for ii=1:lint
polyint=conv(polyint,[1 -1]);
end;
% A megoldandó diophantoszi polinomegyenlet (R1' = R1prime):
% A * polyint * R1prime + Bminus * S = Am * A0
% A lehetséges szorzásokat elvégezve az általános diophantoszi egyenlet formája:
% polyA * R1prime + polyB * S = polyC
polyA=conv(A,polyint) % A diophantoszi egyenletben szereplő A polinom
polyB=Bminus % A diophantoszi egyenletben szereplő B polinom
polyC=conv(Am,Ao) % A diophantoszi egyenletben szereplő C polinom
% A fenti egyenlet átírható lineáris egyenletrendszer alakba, ami mátrixos formában könnyen megoldható.
% Cél: A polinomegyenletnek megfelelő dioA * x = dioB lineáris egyenletrendszer mátrixainak összeállítása.
% A toeplitz(C,R) függvény olyan Toeplitz-mátrix-szal tér vissza, melynek első oszlopa C, első sora pedig R.
% Ha C(1) és R(1) nem egyezik meg, akkor figyelmeztetés mellett C(1) értéke lesz a mátrix (1,1) indexű eleme.
% Esetünkben az dioA mátrix két Toeplitz blokkból áll.
% Az ismeretlenek száma összesen 6-ra adódik - R1' és S polinomok ismeretlenjei.
% Egy Polinom ismeretlenjeinek száma = fokszám + 1.
% Mivel R1' monic polinom, azaz legmagasabb fokszámú tagjának a szorzója 1-es,
% így hiába másodfokú, csak 2 ismeretlen van benne.
% Mivel 6 ismeretlenünk van, így mindkét Toeplitz blokk sorainak száma 6, az első blokk oszlopainak száma 2
% (R1' ismeretlenjeinek száma), a másodiké pedig 4 (S ismeretlenjeinek a száma).
% A toeplitz blokkok paramétereinek megadásaikor, így megfelelő számú 0-t kell beszúrnunk az oszlop
% paraméterként megadott (polyA illetve Bminus) polinomok után úgy, hogy azok elemszáma 6 legyen.
% A sor paraméterként megadott polinomok első eleme Am(1) illetve Bminus(1), ezek után még annyi 0-ást
% kell beszúrnunk, hogy a vektorok elemszáma R1' illetve S ismeretlenjeinek számára egészüljön ki.
% Jelen esetben ez 1 illetve 3 darab NULLA beszúrását jelenti.
% Hogyan is néz ez ki?
% (1 0 | b0 0 0 0 ) (r1) (c1-a1)
% (a1 1 | b1 b0 0 0 ) (r2) (c2-a2)
% (a2 a1 | b2 b1 b0 0 ) (s0) (c3-a3)
% (a3 a2 | 0 b2 b1 b0) * (s1) = (c4-a4)
% (a4 a3 | 0 0 b2 b1) (s2) (c5 )
% (0 a4 | 0 0 0 b2) (s3) (c6 )
dioA=[toeplitz([polyA 0],[polyA(1) 0])...
toeplitz([Bminus 0 0 0],[Bminus(1) 0 0 0])]
% Általános megoldás - csak ínyenceknek!
dioA=[toeplitz([polyA zeros(1,length(polyC)-length(polyA)-1)],...
[1 zeros(1,grR1prime-1)])...
toeplitz([polyB zeros(1,length(polyC)-length(polyB)-1)],...
[polyB(1) zeros(1,grS)])];
% Most a jobb oldalon álló vektor első négy eleme polyC(2)-polyA(2) ... polyC(5)-polyA(5)
% (polyA és polyC első eleme 1, amit nem használunk fel), a további sorokban pedig polyC(6) és
% polyC(7) áll, mivel polyA egy negyedfokú polinom, így nincsenek további együtthatói.
% A legegyszerűbb ezt a vektort olyan módon számítani, hogy polyC 2..7-ik eleméből kivonunk
% egy olyan vektort, ami polyA 2..5-ik eleme után két 0-t tartalmaz. Ügyelni kell arra, hogy a
% polinomokat sorvektorként ábrázoljuk, azonban a lineáris egyenletrendszer jobb oldalán oszlopvektor
% áll, így az eredményt transzponálnunk kell.
dioB=[polyC(2:end)-[polyA(2:end) 0 0]]'
% Általános megoldás - csak ínyenceknek!
% A polyA elemei után beszúrandó 0-k számát a két polinom fokszámkülönbsége
% (a vektorok hosszának különbsége) alapján határozzuk meg.
dioB=polyC(2:end)'-[polyA(2:end) zeros(1,length(polyC)-length(polyA))]';
% Az egyenletrendszer megoldása:
dioSol=inv(dioA)*dioB
% Ínyenceknek:
% dioSol=dioA\dioB
% A 'backslash' jel hatására a Matlab stabilabb és gyorsabb algoritmussal dolgozik!
A szabályzó átviteli függvényék polinomjainak meghatározása
% A dioSol vektor most a következő elemeket tartalmazza:
% dioSol=[r1 r2 s0 s1 s2 s3]'
% Ne feledjük, hogy a megoldás is oszlopvektor formában adódott!
% R1' számítása:
% R1' másodfokú, ám mivel monic, ezért legnagyobb fokszámú együtthatója 1, így csak a további 2
% együttható szerepel a megoldásvektorban. R1prime vektor polinomnak felel meg, így sorvektornak
% kell lennie, úgyhogy transzponálnunk kell a megoldásvektor elemeit
R1prime=[1 dioSol(1:2)']
% R polinom számítása:
% R = Bplus * (z-1)^l * R1'
R=conv(conv(Bplus,polyint),R1prime)
% S polinom számítása:
% S együtthatóit a megoldásvektor 3..6-ik elemei tartalmazzák, de a vektort
% még transzponálnunk kell, hogy S vektor sorvektor legyen
S=dioSol(3:6)'
% T polinom számítása:
T=Bmprime*Ao % Bmprime egy skalár, így nincs szükség a conv-ra
% Általános megoldás - csak ínyenceknek!
% R1prime=[1 dioSol(1:grR1prime)'];
% S=dioSol(grR1prime+1:end)';
A zárt szabályozási kör összeállítása
%% A zárt szabályozási kör összeállítása
d_ff=tf(T,R,Ts) % Szabályozó az előrevezető ágban
d_fb=tf(S,R,Ts) % Szabályozó a visszacsatoló ágban
d_cl=d_ff*feedback(dp,d_fb,-1); % A zárt kör számítása
d_cl=minreal(d_cl) % PZ-kiejtés
figure(1);
step(d_cl); % A zárt kör ugrásválasza
xlabel('t');
ylabel('y');
figure(2);
pzmap(d_cl); % A csillapítás és frekvencia leolvasható és ellenőrizhető
% A beavatkozó jelre vonatkozó átviteli függvény zárt körben
d_u=d_ff*feedback(tf(1,1),dp*d_fb);
figure(3);
step(d_u); % A beavatkozó jel egységugrás alapjel esetén
xlabel('t');
ylabel('u');
% A kétszabadságfokú szabályzó működését definiáló differenciaegyenlet, azaz a beavatkozó jel
% aktuális értékének számítására vonatkozó képlet:
% u = T/R * r - S/R * y --> R*u = T*r - S*y
% A feladat során kiszámolt R(z), T(z) és S(z) polinomok behelyettesítése:
%
% (1*z^3 - 1.13*z^2 + 0.22*z - 0.09)*u = (0.88*z^3 - 0.97*z^2 + 0.36*z - 0.04)*r -
% (317*z^3 - 863*z^2 + 781*z - 235)*y
%
% Leosztunk (z^3)-el, elvégezzük az inverz Z-transzformációt és u[k]-ra rendezzük az egyenletet:
%
% u[k] = 0.88*r[k] - 0.97*r[k-1] + 0.36*r[k-2] - 0.04*r[k-3] -
% 317 *y[k] + 863 *y[k-1] - 781 *y[k-2] + 235 *y[k-3] +
% 1.13*u[k-1] - 0.22*u[k-2] + 0.09*u[k-3]
A robosztusság illusztrációja
% A szakasz minden paraméterét 25%-al megnöveljük illetve lecsökkentjük
wp125=tf(Aplant,conv(conv([1.25*T1 1],[1.25*T2 1]),[1.25*T3 1]));
wp75=tf(Aplant,conv(conv([0.75*T1 1],[0.75*T2 1]),[0.75*T3 1]));
dp125=c2d(wp125,Ts);
dp75=c2d(wp75,Ts);
% Zárt körök összeállítása a pertubált szakaszokból és az eredeti szabályzóból
d_cl75=series(d_ff,feedback(dp75,d_fb,-1));
d_cl125=series(d_ff,feedback(dp125,d_fb,-1));
% A beavatkozó jelre vonatkozó átviteli függvények
d_u75=series(d_ff,feedback(tf(1,1),dp75*d_fb));
d_u125=series(d_ff,feedback(tf(1,1),dp125*d_fb));
% Az ugrásválaszok ábrázolása
figure(4);
step(d_cl,d_cl75,d_cl125);
legend('Nominalis rendszer','75%','125%');
xlabel('t');
ylabel('y');
figure(5);
step(d_u,d_u75,d_u125);
legend('Nominalis rendszer','75%','125%');
xlabel('t');
ylabel('u');