Számítógépes látórendszerek - Ellenőrző kérdések: Képillesztés

← Vissza az előző oldalra – Számítógépes látórendszerek

Ismertesse az optikai áramlás (optical flow) algoritmus célját, alapelvét és feltételezéseit!
Írja fel az intenzitás áramlás egyenletet!
Milyen problémái vannak az algoritmusnak?

Az intenzitásalapú képillesztés alapelve, az hogyha találunk a két képen két ugyanolyan színű területet, akkor ezek egymással megfeleltethetők (ez azonban csak erős feltételezés). Lehetséges módszer az optikai áramlás algoritmus, amikor is pontpárokat két, különböző időben készült felvételen keressük és a mozgást próbáljuk leírni. Az adott pixelt a következő képen az előző pozíciójának közelében keressük. Gradiensképzést alkalmazunk.

Feltételezések:

• Az egyes objektumok intenzitása időben állandó.
• A két képkocka közti elmozdulás kicsi.
• Az egymáshoz közel eső pixelek hasonlóan mozognak.

Az optikai áramlás nem működik:

• Homogén intenzitású területen.
• Túl nagy mozgás esetén.
• Apertúra probléma.

Az intenzitás áramlás egyenlete:

$I_{x}u+I_{y}v=-I_{t}$

Mutassa be a Lucas-Kanade algoritmust és annak célját!
Milyen módszereket ismer a gyors mozgások követésére optikai áramlás segítségével?

Az optikai áramlás algoritmusánál feltételeztük, hogy az egymáshoz közeli pixelek azonos objektumhoz tartoznak, ezért együtt mozognak. Ne a pixelt nézzük, hanem a környezetét! Több pont együttes kezelése esetén az alulhatározott egyenletből túlhatározott lesz (Lucas-Kanade módszer).

A környezet elmozdulásának négyzetes hibáját minimalizáljuk. Parciális derivált = 0 helyen optimum.

$E=\sum {\left(uI_{x}+vI_{y}+I_{t}\right)^{2}}\rightarrow Min$

${\frac {\partial E}{\partial u}}=0\;\;\;{\frac {\partial E}{\partial v}}=0$

${\begin{bmatrix}\sum I_{x}^{2}&\sum I_{x}I_{y}\\\sum I_{x}I_{y}&\sum I_{y}^{2}\end{bmatrix}}\cdot {\begin{bmatrix}u\\v\end{bmatrix}}={\begin{bmatrix}-\sum I_{x}I_{t}\\-\sum I_{y}I_{t}\end{bmatrix}}$

$H{\vec {u}}=b\to {\vec {u}}=H^{-1}b$

Az Lucas-Kanade egyenlet megoldható, ha Az H sajátértékei nem túl kicsik (vagy nullák) és a H sajátértékeinek aránya nem túl nagy (H jól kondicionált).

Egyéb módszerek a gyors mozgások követésére:

• Iteratív Lucas-Kanade algoritmus.
• Optical Flow piramis.

Mit nevezünk sarokszerű képrészletnek?
Ismertesse a Harris operátor elvét és lépéseit!

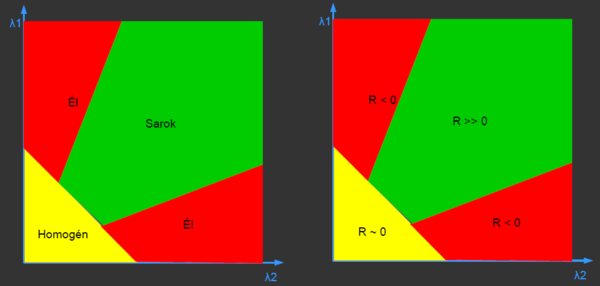
Mi a képi sarok?

• Él: Ahol valamilyen irányban az intenzitásban egy ugrás van.
• Sarok: Ahol az intenzitás minden irányban ugrik!

Harris detektor alapelve:

• Vegyünk egy ablakot a pont körül.
• Mozgassuk el minden irányba, és számoljuk ki a hibát a kép és az ablak közt.
• Ha minden irányban nagy a hiba, akkor sarokpontunk van.

$R=det(H)-k\cdot trace(H)^{2}$

$k\in [0,04-0,06]$

Milyen képtranszformációkat ismer?
Ezek közül melyekre invariáns a Harris operátor?

• Intenzitásváltozás:
  • Additív intenzitásváltozás: $I\to I+b$
  • Multiplikatív intenzitásváltozás: $I\to aI$
  • Csak részlegesen invariáns rá a Harris detektor.
• Forgatás:
  • A sajátvektorok változnak, de a sajátértékek nem!
  • Invariáns rá a Harris detektor.
• Skálázás:
  • Nincs invariancia!

Ismertesse a SIFT eljárás képrészletdetektáló részét!
Hogyan érjük el a skála invarianciát és a szubpixeles pontosságot?

SIFT = Scale Invariant Feature Transform

• Keressünk kulcspontokat
  • Érdekes (sarokszerű) legyen
  • Keressünk skálainvariáns módon
• Készítsünk minden régióhoz egy leírót, ami intenzitás, skála és rotáció invariáns

Sarokdetektálást végezzünk el több skálafaktor mellett. Ezt a skálafaktort tároljuk el az egyes jellemzőkhöz. Difference of Gaussians, azaz két eltérő szélességű (szórású) gauss szűrő különbsége - Valóságban gauss-szal szűrt képek kivonása. A DoG szűrő maximuma ott lesz a skálatérben, ahol az objektum mérete egybeesik a szűrő inflexiós pontjával → Ez lesz a jó skála!

Kulcspontok pozíciójában szubpixeles pontosságot követelünk meg! Interpolációra lesz szükség három dimenzióban (x,y,skála)

Az így megtalált kulcspontokat szűrni kell! Nem elég kontrasztos régió. Élszerű régió (sajátértékekkel).

Mutassa be a SIFT algoritmus leíró generáló részét! Hogyan érjük el a forgatás invarianciát?

A leírót a kulcspont 16x16-os környezetéből készítjük. A leírónak is invariánsnak kell lennie! A leírót ezért a kulcspont skálafaktorához tartozó képből készítjük.

• Minden pixelre kiszámoljuk a gradiens nagyságát és irányát.
• A kulcspont körül gradienshisztogramot készítünk, ami 36 rekeszből áll(10fok egy rekesz).
• Az egyes rekeszekhez az adott irányban lévő gradiens értékeket adjuk hozzá, és ezeket még súlyozzuk a kulcsponttól való távolsággal.

A jellemző orientációja az így készült hisztogram maximumánál lesz.

A leírót úgy generáljuk, hogy egy 16x16 os képrészletet 4x4-es részekre osztjuk, és azokban számoljuk a fenti metódussal az orientációkat. Ezekből álll össze a leíró vektor.