Laboratórium 2 - 8. Mérés ellenőrző kérdései

← Vissza az előző oldalra – Laboratórium 2

← Vissza az előző oldalra – Laboratórium 2 - 8. Mérés: Rendszer-identifikáció és szabályozás

1. Milyen identifikációs rendszermodelleket ismer?

AR, ARX, IV, ARMAX stb. Ezek a modellek a MATLAB System Identification (röviden IDENT) toolboxa segítségével identifikálhatók. ARX modell a klasszikus LS (least squares) becsléssel is identifikálható. A módszerek érzékenyek a jel és zaj korreláltságára, amelyen segédváltozók (IV) alkalmazásával lehet javítani. Az ARMAX modell már általánosabb zajstruktúrát alkalmaz, de identifikációja numerikusan bonyolultabb módszert igényel, nevezetesen a kvázi Newton-módszert. Lásd elméleti alapok.

2. Miért van szükség identifikációra?

Az identifikáció célja dinamikus modell nyerése az ismeretlen rendszerről, a szabályozástechnikában a szabályozott szakaszról. Dinamikus modell hiányában csak kísérletezéssel tudnánk egyszerű szabályozók paraméterbeállítását megkeresni. A dinamikus modell ismerete lehetővé teszi elméletileg megalapozott szabályozások tervezését, amely minimálissá teszi a reális folyamaton való kísérletezést. A modell jó, ha azonos bemenő jel mellett a kimenetén hasonlóan válaszol, mint az ismeretlen rendszer. A modellel szemben pótlólagos elvárásaink is lehetnek, mint például az, hogy az identifikációval kapott diszkrétidejű modellnek legyen folytonosidejű megfelelője. Ez a negatív valós pólusokkal áll kapcsolatban a z-tartományban.

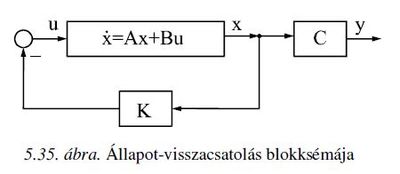
3. Mit értünk állapot-visszacsatolás alatt?

Állapot-visszacsatolás alatt azt értjük, hogy a szabályozó kimenő jelét (a beavatkozó jelet) az állapotokból állítjuk elő. Lineáris állapot-visszacsatolás esetén folytonos időben [math]u(t)=-K\cdot x(t)[/math], diszkrét időben pedig [math]u(iT)=-K\cdot x(it)[/math], vagy röviden [math]u_i=-K\cdot x_i[/math], ahol T a mintavételi idő. Egyváltozós (SISO) rendszer esetén K sorvektor.

4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete?

Folytonos időben:

• A szakasz állapotegyenlete: [math]\dot{x}=Ax + Bu[/math]
• A zárt rendszer állapotegyenlete: [math]\dot{x}=(A-BK) \cdot x[/math]
• A zárt rendszer karakterisztikus egyenlete: [math]\varphi_c(s)=det \; (sI-(A-BK))[/math]

Diszkrét időben:

• A szakasz állapotegyenlete: [math]x_{i+1}=\Phi x_i + \Gamma u_i[/math]
• A zárt rendszer állapotegyenlete: [math]x_{i+1}=(\Phi-\Gamma K) \cdot x_i[/math]
• A zárt rendszer karakterisztikus: [math]\varphi_c(z)=det \; (zI-(\Phi - \Gamma K))[/math]

A pólusáthelyezési feladatban előírjuk a zárt rendszer karakterisztikus egyenletét (ami ekvivalens a zárt rendszer pólusainak, azaz a velük megegyező sajátértékeknek az előírásával), és keressük az ehhez szükséges állapot-visszacsatolást. Vegyük észre az algebrai hasonlóságot a folytonos idejű és diszkrét idejű feladat esetén.

5. Mik a fő problémák az egyszerű u=-Kx állapot-visszacsatolás esetén tipikus irányítási rendszerekben?

Az egyik probléma az, hogy az állapotvektornak az összes komponense általában nem mérhető, például SISO esetben csak a kimenő jelet méri egy érzékelő, ezért állapotmegfigyelőt célszerű alkalmazni a becslés előállítására és bevonásába a beavatkozó jel számításába. A másik probléma, hogy az egyszerű állapot-visszacsatolás nem veszi figyelembe az alapjelet (más néven referencia jelet), ezért pótlólagos figyelembevételéről külön kell gondoskodni, lásd [math]N_x,N_u[/math]

6. Mi a domináns póluspár?

A szabályozási kör [math]s_{1,2}=- \sigma_e \pm j \omega_e[/math] póluspárját dominánsnak nevezzük, ha a zárt szabályozási kör dinamikus minőségi jellemzőit lényegében [math]s_{1,2}[/math] határozza meg. Ennek feltétele, hogy a többi stabil pólusra teljesüljön [math]\left|Re \left\{ s_i \right\} \right| \gt 3 \sigma_e[/math], mert ekkor a többi pólus okozta tranziens már lecseng az első maximumig terjedő időpont [math](T_m)[/math], a túllövés [math](\Delta v)[/math] és a beállási idő [math](T_{2 \%} )[/math] számításakor. Ebben az esetben jó közelítéssel:

[math]T_m={\pi \over \omega_e}[/math]

[math]\Delta v = \exp \left( {-\pi \sigma_e \over \omega_e} \right) = \exp \left( { - \pi \xi \over \sqrt{ 1- \xi^2 } } \right)[/math]

[math]T_{2\%}={\ln(50) \over \sigma_e } \approx {5 \over \sigma_e}[/math]

7. Mi a kapcsolat a kéttárolós lengő tag csillapítása és csillapítatlan sajátfrekvenciája valamint a hozzátartozó pólusok között?

A kéttárolós lengő tag átviteli függvénye:

[math]W(s)={\omega_0^2 \over s^2 + 2 \xi \omega_0 s + \omega_0^2 }[/math]

Pólusai: [math]s_{1,2}=-\sigma_e \pm j \omega_e= - \xi \omega_0 \pm j \omega_0 \sqrt{1 - \xi^2}[/math]

Csillapítás: [math]0\lt \xi\lt 1[/math]

Csillapítatlan sajátfrekvencia: [math]\omega_0 = {1 \over T}[/math]

Aszimptotikus amplitúdó menete az [math]\omega_0[/math] helyen törésfrekvenciával rendelkezik, rezonanciahelye és az amplitúdó értéke a rezonancia helyén [math]\xi[/math]-től függ.

Nincs rezonancia, ha [math]\xi \geq {1 \over \sqrt{2} } \approx 0.707[/math].

A [math]v(t)[/math] átmeneti függvénynek ezzel szemben [math]\Delta v \gt 0[/math] túllövése van, ha [math]\xi \lt 1[/math]

8. Mi biztosítja a konstans alapjel követését állapot-visszacsatolt rendszerekben?

Hiba a bélyegkép létrehozásakor: Nem lehet a bélyegképet a célhelyre menteni

Az [math]r = y_{\infty}[/math] alapjel követést az [math]N_x r[/math] és az [math]N_u r[/math] jelek biztosítják az állapot-visszacsatolt rendszerben, ahol [math]N_x r = x_{\infty}[/math] és [math]N_u r = u_{\infty}[/math].

Diszkrét időben ezeket a következő feltételből lehet meghatározni:

[math] \left[ \begin{array}{rr} N_x \\ N_u \end{array} \right] = \left[ \begin{array}{rr} \Phi-I & \Gamma \\ C & 0 \end{array} \right]^{-1} \cdot \left[ \begin{array}{rr} 0_{n \times m} \\ I_{m \times m} \end{array} \right][/math]

9. Miért szükséges állapotmegfigyelő alkalmazása?

Az [math]x[/math] állapotvektornak általában nem mérhető az összes komponense, például SISO esetben csak a kimenő jelet méri egy érzékelő, ezért állapotmegfigyelőt célszerű alkalmazni a becslés előállítására és bevonásába a beavatkozó jel számításába folytonos időben [math]u = - K \hat{x}[/math] , diszkrét időben pedig [math]u_i = -k \hat{x}_i[/math] alakban. Az állapotmegfigyelő egy dinamikus rendszer, amelynek kimenete a becsült állapot, bemenete pedig a szakasz kimenete és a beavatkozó jel.

10. Mi a kapcsolat a "terhelés" elnevezés és a zavaró jel között?

Terhelés alatt a szabályozott szakasz bemenetére redukált [math]d[/math] zavaró jelet értjük.

11. Hogyan küszöbölhető ki a terhelés hatása?

Ha az állapotmegfigyelő becsülni tudja a bemenetre redukált [math]d[/math] zavarást is, akkor jó becslés esetén a szabályozó kimenetéhez hozzáadva a terhelés [math]- \hat{x}_d[/math] becslését, a [math]d[/math] zavarást kompenzálja a [math]- \hat{x}_d[/math] , és a rendszer úgy viselkedik, mintha nem is lenne zavarás.

12. Mit értünk diszkrétidejű aktuális megfigyelő alatt és mik az előnyei?

A diszkrétidejű aktuális állapotmegfigyelő állapotegyenlete:

[math]\hat{x}_i = F \hat{x}_{i-1} + G y_i + H u_{i-1}[/math]

Ha [math]\tilde{x} = x - \hat{x}[/math] a becslési hiba, akkor [math]F=\Phi - GC\Phi, \; H=\Gamma - GC\Gamma[/math] választás esetén, ha a gerjesztetlen [math]\tilde{x}_i=F \tilde{x}_{i-1}[/math] rendszer stabil és gyors, akkor rövid tranziens után a becslési hiba eltünik, és az állapot-visszacsatolásban [math]x[/math] helyettesíthető a vele már megegyező [math]\hat{x}[/math] becsült állapottal.

Az aktuális megfigyelő előnye, hogy [math]\hat{x}_i[/math] számításakor már figyelembe veszi az aktuális [math]y_i[/math] kimenő jelet, és ezáltal egy mintavételi időnyi holtidőt eliminál az irányítási algoritmusban, ami gyorsabb működést eredményezhet.

Mivel [math]\varphi_0(z)=\det (zI-F)=\det \left( zI - F^T \right) =\det \left( zI- \left( \Phi^T - \Phi^T C^T G^T \right) \right)[/math] , ezért az aktuális állapotmegfigyelő tervezése algebrailag hasonló a pólusáthelyezési feladathoz, azaz előírt [math]\varphi_0(z)[/math] esetén a fiktív [math]\left( \Phi^T, \Phi^TC^T \right)_{II}[/math] rendszerhez kell [math]K_{II}=G^T[/math] fiktív állapot-visszacsatolást tervezni.

13. Miért érdemes integrátort tenni a szabályozási körbe?

A szabályozási körbe integrátort helyezve javulnak az alapjel követési és zavaró jel elnyomási tulajdonságok, ha biztosítjuk a zárt rendszer stabilitását is. Az integrátor javítja a lassú paraméterváltozásokkal szembeni robusztusságot is mindaddig, amíg a paraméterváltozások ellenére a zárt rendszer stabil marad. Ennek oka, hogy az integrátor miatt a felnyitott kör erősítése alacsony frekvencián nagy (nulla frekvencián végtelen). Másrészt viszont alacsonyfrekvenciás pólus/zérus pár léphet fel a zárt rendszer átviteli függvényében, ami a dinamikus minőségi jellemzők romlásához vezethet.

14. Hogyan képződik le egy folytonos idejű pólus a diszkrétidejű tartományba?

A folytonosidejű [math]s_i[/math] pólus a [math]z_i = \exp(s_iT)[/math] helyre képződik le a pólusok számának és multiplicitásának megőrzése mellett.

Mivel [math]s_i=(\ln z_i) /T[/math] , ezért páratlan multiplicitású negatív valós [math]z_i[/math] pólusú diszkrétidejű rendszernek nincs folytonosidejű megfelelője.

15. Mit okoznak a megfigyelő sajátértékei a zárt rendszer átviteli függvényében?

A megfigyelő sajátértékei a zárt rendszer átviteli függvényében pólus/zérus kiejtést okoznak.

A zárt rendszernek az egyszerűsítés után megmaradó pólusai a K állapot-visszacsatolás tervezésénél specifikált [math]\varphi_c[/math] polinom gyökei lesznek, vagyis az állapotmegfigyelő alkalmazása nem módosítja a zárt rendszer megtervezett pólusait (feltéve, hogy a szabályozott szakasz modelljét pontosan ismerjük).