Fizika 3 - Vizsga, 2011.01.13.

Kiskérdések

1. Mekkora annak a fotonnak a hullámhossza, amely képes ionizálni a H atomot?

$E=13,6eV=h\nu =h{\frac {c}{\lambda }}$

$\lambda ={\frac {hc}{E}}=...$

2. Ha egy 1 eV energiájú foton ütközik egy szabad állapotban lévő elektronnal, akkor maximum mennyi energiát adhat át neki?

A beérkező foton energiájából megkapjuk a hullámhosszát:

$E=1eV=h\nu _{1}=h{\frac {c}{\lambda _{1}}}$

$\lambda _{1}={\frac {hc}{E}}$

Nyilván Compton effektusos példa, maximális az energia átadás, ha $\theta =180^{o}$, ebből kiszámolhatjuk a szóródott foton hullámhosszát.

$\Delta \lambda =\Lambda (1-\cos \theta )$

$\lambda _{1}-\lambda _{2}=\Lambda (1-\cos \theta )$

$\lambda _{1}-\lambda _{2}=2\Lambda$

$\lambda _{2}=2\Lambda -\lambda _{1}$

Az energia megmaradásból megkaphatjuk az átadott energiát:

$h\nu _{1}=h\nu _{2}+E_{elektron}$

$E_{elektron}=1eV-h{\frac {c}{\lambda _{2}}}$

3. Definició alapján egy szabadon mozgó elektron valószínűségi áramsűrásége

Ebbe:

${\bar {J}}={\frac {\hbar }{2\cdot m\cdot j}}\cdot \left({{\Psi ^{*}}\cdot \nabla \Psi -\Psi \cdot \nabla {\Psi ^{*}}}\right)$

kéne behelyettesíteni a szabadon mozgó elektron állapotfüggvényét:

$\Psi (x,t)=\psi (x)\cdot \theta (t)=A\cdot {e^{j\cdot k\cdot x}}\cdot {e^{{\frac {E}{\hbar }}\cdot t}}$

Ez csak tipp, nem csináltam meg vizsgán.

4. Lineáris oszcilátor minimum 2eV energiájú fotont tud elnyelni, adja meg a 5eV energiaszinthez tartozó állapotfüggvény matematikai alakját.

a lépésköz 2 eV, a 0. állapot 1/2 hávonás omega, azaz 1eV, tehát az 5 eV a 2. állapot, ehhez tartozó függvény valami hermite polinómos módszerrel, vagy kitudja...

5. Mérés várható értékének értelmezése

$\langle A\rangle _{\phi }=\sum _{i=0}^{\infty }\left|a_{i}\right|^{2}A_{i}=\sum _{i=0}^{\infty }\left|\langle \alpha _{i},\varphi \rangle \right|^{2}A_{i}$

Ahol a_i a fi A operátor sajátbázisbeli együtthatói, A_i pedig a sajátértékek. Meg talán a szép ábra is kell.

6. Ábrázolja szabadon mozgó részecske Vo potenciálgáton való áthaladási valószínűségét

Transzmissziós tényező grafikonja

Nem a Gamow közelítés, hanem a pontosabb kell, ami már figyelembe veszi a differenciál folytonossági kritériumot is. Valami ilyesmi az ábra:

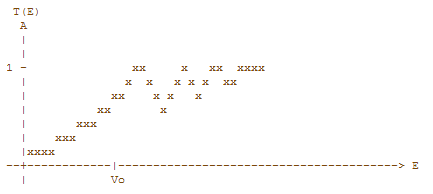
7. Spin és pálya perdületének precessziós mozgásának körfrekvenciája

Larmour (a pályáé) és cikloton (spin) körfrekvencia

$\omega _{L}=-{\frac {eB}{2m}}$

$\omega _{c}=-{\frac {eB}{m}}$

8. Kiválasztási szabályok

Jó kérdés, mi ez egyáltalán?

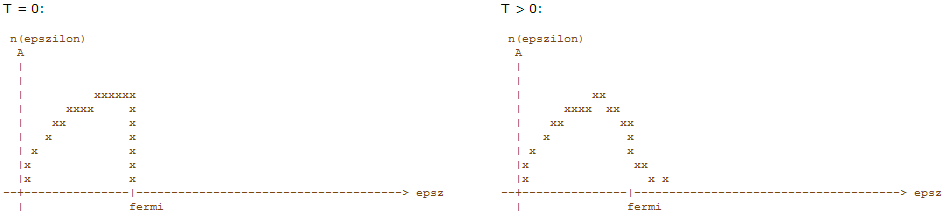
9. Elektrongáz grafikonja T = 0 és T > 0 hőmérsékleten

10. Pauli mátrixok

${\hat {S}}_{x}={\frac {hvonas}{2}}\left[{\begin{array}{rr}0&1\\1&0\end{array}}\right]$

${\hat {S}}_{x}={\frac {hvonas}{2}}\left[{\begin{array}{rr}0&-j\\j&0\end{array}}\right]$

${\hat {S}}_{x}={\frac {hvonas}{2}}\left[{\begin{array}{rr}1&0\\0&-1\end{array}}\right]$

Nagykérdések

1. A kvantummechanika posztulátumai
2. Khi ASZ és Khi SZ spinpálya állapotok lehetséges értékei
3. Vezesse le a perturbáció számítás elsőrendű közelítését 2 degeneráltságú állapot esetén.
4. Kicserélési energia
5. Bloch állapotok LCOA közelítéssel, 1D eset
6. Szilícium kristály sávszerkezetének kialakulását mutató ábra, kötő és lazító pályákkal