Algoritmuselmélet - PPZH, 2013.05.23.

← Vissza az előző oldalra – Algoritmuselmélet

2013.05.23 - PPZH megoldásai

1. Feladat (Van megoldás)

Tudjuk, hogy az Értelmezés sikertelen (ismeretlen „\textsc” függvény): {\displaystyle f(n), g(n) : \textsc{N} \rightarrow \textsc{N} } függvényekre igaz, hogy $f(n)=\mathrm{\Omega }(logn)$ és $g(n)=\mathrm{\Theta }(n^4).$ Lehetséges-e, hogy:

(a) $f(n)=\mathrm{\Theta }(g(n))?$

(b) $g(n)=O(f(n))?$

(Ez két, egymástól függetlenül megválaszolandó kérdés.)

Megoldás

a)

• Ha $f(n)=n^4,g(n)=n^4$
• Akkor igaz az, hogy:
  • $f(n)=\mathrm{\Omega }(logn)\Rightarrow n^4=\mathrm{\Omega }(logn)$
  • És az is, hogy $f(n)=\mathrm{\Theta }(g(n))\Rightarrow n^4=\mathrm{\Theta }(n^4)$
• Tehát lehetséges.

b)

• Ha $g(n)=n^4,f(n)=n^4$
• Akkor igaz az, hogy:
  • $g(n)=\mathrm{\Theta }(n^4)\Rightarrow n^4=\mathrm{\Theta }(n^4)$
  • És az is, hogy $g(n)=O(f(n))\Rightarrow n^4=O(n^4)$
• Tehát lehetséges.

2. Feladat

TODO

Megoldás

TODO

3. Feladat

TODO

Megoldás

TODO

4. Feladat

TODO

Megoldás

TODO

5. Feladat

Egy kupac elemeit preorder bejárás szerint kiolvasva az alábbi számsorozatot kapjuk: $1,17,19,21,22,31,37,2,8,3.$ Rekonstruálható-e ebből a kupac?

Megoldás

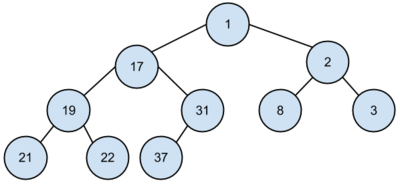
• A kupac egy teljes bináris fa, így tudjuk, hogy mi a fa alakja.
• Nincs is más dolgunk, mint felrajzolni, majd a preorder bejárás alapján beírni az elemeket a megfelelő csúcsokba, és ellenőrizni, hogy sérül-e valahol a kupac adatszerkezet egy tulajdonsága.

• Látszik, hogy minden rendben van, így a kupac rekonstruálható.

6. Feladat

TODO

Megoldás

TODO

7. Feladat

TODO

Megoldás

TODO

8. Feladat

TODO

Megoldás

TODO