Infokommunikáció - Vizsga, 2014.01.07.

← Vissza az előző oldalra – Infokommunikáció

A 2014. január 7-i Infokommunikáció-vizsga feladatai és megoldásai. A 2. és 9. feladat három, a többi két pontot ér.

1. feladat

Adott egy kód, mely a 2 bites üzenetekből a következő kódszavakat álltja elő:

• 00: 00000
• 01: 01110
• 10: 10101
• 11: 11???

a) Adja meg a kód szisztematikus generátormátrixát! v=(01010) vett szó esetén melyik kódszó lett kiküldve a legnagyobb valószínűséggel?

Megoldás

k=2 (üzenethossz), n=5 (kódszóhossz)<br\> A G szisztematikus generátormátrix azon két kódszóból áll, melyeknek első 2-2 bitjéből egységmátrix alakítható ki. Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle G= \left[ \begin{matrix} 1 & 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 1 & 0 \end{matrix} \right]} Az első két oszlop egy k-s egységmátrix, a harmadik-ötödik sorok pedig B mátrixot alkotják. <br\>

A 01110 kódszó csak 1 bitben tér el v-től, míg a többi több bitben, így valószínűleg ez lett kiküldve.

b) Adja meg a paritásellenőrző mátrixot! A fenti v-re adja meg a szindrómát!

Megoldás

A paritásellenőrző mátrix B transzponáltjának és egy (n-k)-s egységmátrixnak egymás mellé rakásából alakul ki. Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle H=\left[ \begin{matrix} 1 & 1 & 1 & 0 & 0\\0 & 1 & 0 & 1 & 0\\1 & 0 & 0 & 0 & 1 \end{matrix} \right] } <br\>

A szindróma: Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle S=H*v^T=\left[ \begin{matrix} 1 & 1 & 1 & 0 & 0\\0 & 1 & 0 & 1 & 0\\1 & 0 & 0 & 0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 0 \\ 1 \\ 0 \\ 1 \\ 0 \end{matrix} \right]= \left[ \begin{matrix} 1 & 0 & 0 \end{matrix} \right]}

2. feladat

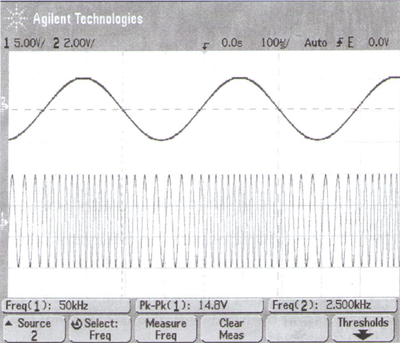
<br\><br\> a) Frekvencia- vagy fázismodulált a képen látható jel? Miért?

Megoldás

Frekvenciamodulált, mert a moduláló jel függvényében változik a modulált jel frekvenciája (sűrűsödnek/ritkulnak a nullátmenetek).

b) Becsülje meg a jel frekvencia- és fázislöketét!

Megoldás

???

c) Milyen demodulátort javasolna? Rajzolja fel a blokkvázlatát!

Megoldás

Pl: számláló típusú demodulátort.

3. feladat

Egy a 900 MHz-es sávban működő vevőantennával az interferenciazóna határán dolgozunk. Az antenna 5 m magasan van.<br\> a) Hány dB-vel változik a teljesítmény, ha a vevőantennánk magasságát felére csökkentjük?

Megoldás

Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle |E_r|=2*|E_0|*|\sin(\frac{2*h_t*h_r}{\lambda*r})|} Az interferenciazóna határán a szinusz argumentuma pontosan Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{\pi}{2}} , tehát Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle |E_{rmax}|=2*|E_0|} . Ha felére csökkentjük h_r értékét, a szinusz argumentuma is feleződik. Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle |E_r|=2*|E_0|*\sin(\frac{\pi}{4})=2*|E_0|*\frac{\sqrt{2}}{2}=|E_{rmax}|*\frac{\sqrt{2}}{2}}

A teljesítmény a térerősség négyzetével arányos, tehát az eredeti állapothoz képest feleződni fog, ami 3 dB-es csökkenést jelent.

b) Hány dB-vel változik a teljesítmény, ha a vevőantennánk magasságát kétszeresére növeljük?

Megoldás

Az előbbi képletbe kétszeres h_r-t helyettesítve a szinusz argumentuma Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \pi} lesz. Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle |E_r|=2*|E_0|*\sin{\pi}=0 \frac{V}{m}}

Nulla térerősség esetén a teljesítmény is 0 watt, ami dB-skálán Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle -\infty} . Bármekkora is volt tehát a kezdeti teljesítmény, az antenna magasságának kétszerezése után végtelen decibellel csökkent az értéke.

4. feladat

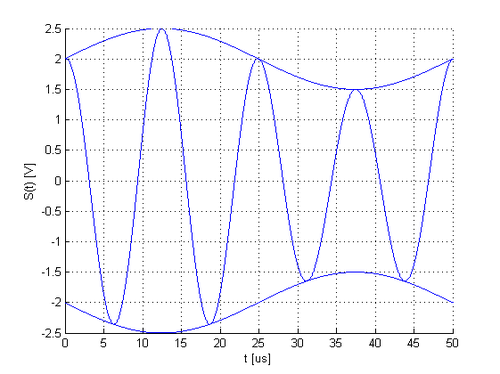
Egy AM-DSB modulált jel frekvenciája 80 kHz, a moduláló jel 20 kHz-es szinuszjel. A modulált jel csúcsértéke 2,5 V, a modulációs mélység 25%.<br\> a) Rajzolja fel a jel egy legalább 50 mikroszekundum hosszú szakaszát!

Megoldás

Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle U_v+A=2.5, A=0.25*U_v \Rightarrow A=0.5 V, U_v=2 V} <br\> Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{1}{20 kHz}=50 \mu s} , tehát a teljes jel 1 periódusa, a vivőjel 4 periódusa fér be a megadott intervallumba.<br\>

b) Írja fel a modulált jel időfüggvényét! Milyen mértékegységben kell beírni az idő értékét? Milyen frekvenciájú összetevői vannak a modulált jelnek, és mennyi ezek amplitúdója?

Megoldás

A frekvencia kHz-ben van megadva, az időt ezért ms-ban kell beírni.<br\> Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle S_{AM}(t)=(2+0.5*\sin(2\pi20t))*\cos(2\pi80t)} <br\> A jel komponensei és amplitúdójuk:

• 80 kHz : 2 V
• 80-20 = 60 kHz : 0,5/2=0,25 V
• 80+20 = 100 kHz : 0,5/2=0,25 V

5. feladat

Szuperheterodin vevő középfrekvenciája 10,7 MHz.<br\> a) Felső keverést alkalmazva hova kell hangolnunk a vevő oszcillátorát, hogy a 107 MHz-es frekvenciájú adót hallgassuk?

Megoldás

Felső keverés: Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle F_o > F_v} , ahol F_v az adó frekvenciája.<br\>

Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle F_o=F_v+f_{KF}=107+10.7=108.7 MHz}

b) Mekkora az előbbi adó tükörfrekvenciája?

Megoldás

Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle F_t=F_v+2*f_{KF}=F_o+f_{KF}=107+21.4=128.4 MHz}

6. feladat

Egy digitális rendszerben a bemenő és a visszaállító szűrő is ideális aluláteresztő jellegű, de sávszélességük nem egyezik meg. A bemenetre 1 kHz-es szimmetrikus négyszögjelet adunk, aminek minden páratlan felharmonikusa létezik az alapharmonikus mellett, de a kimeneten csak 1, 3, 7, 9 kHz-es komponensek jelennek meg.<br\> a) Mekkora lehetett a bemenő és a visszaállító szűrő sávszélessége?

Megoldás

• Nincs 5 kHz-es felharmonikus, de 3 kHz-es van, tehát a bemenő szűrő sávszélessége nagyobb, mint 3 kHz, de kisebb, mint 5 kHz.
• A legnagyobb komponens értéke 9 kHz, tehát a visszaállító szűrő sávszélessége nagyobb 9 kHz-nél.

b) A fenti adatok alapján adja meg a mintavételi frekvenciát!

Megoldás

A mintavételezés során az bemenő szűrő által leszűrt jelünk spektruma f_s egész számú többszörösei körül ugyanúgy megjelenik, ez hozza be a 7 és 9 kHz-es komponenseket a kimeneten (amiket a bemenő szűrő alapvetően levágott). A mintavételi frekvencia egész biztosan 2n MHz alakú, ahol n egész szám. Mivel a bemenő szűrő csak az alapharmonikust és a harmadik felharmonikust engedte át, a mintavételi frekvenciától plusz-mínusz 1 és 3 kHz-re jelennek meg komponensek. 2, 4, 6, 8 kHz-es mintavételezés esetén ez egészen biztosan behozna egy 5 kHz-es komponenst, olyan viszont nincs a kimeneten. A 10 kHz-es mintavételi frekvencia viszont megfelel a követelményeknek: 10-1=9, 10-3=7, amennyiben a kimenő szűrő sávszélessége kisebb, mint 11 kHz (10+1=11, 10+3=13 kHz-es komponensek levágása miatt).

7. feladat

a) Mi a fair queuing előnye a szigorú prioritáskezeléssel szemben?

Megoldás

Nincs éhezés a rendszerben.

b) Mi a WFQ algoritmus előnye a fair queuing-gal szemben?

Megoldás

WFQ = weighted fair queuing, előnye, hogy súlyozott: a fontosabb folyamatok gyakrabban jutnak erőforrásokhoz, mint a kevésbé fontosak.

8. feladat

Egy GSM-rendszerben MS-A1 és MS-A2 is az Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \alpha} hálózat előfizetője, de MS-A2 a Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \beta} hálózatban roamingol.<br\> a)-b) ill. c)-d) együtt érnek 1-1 pontot<br\> a) MS-A1 hívja MS-A2-t. Melyik VLR kerül lekérdezésre a HLR_α által?

Megoldás

VLR_β

b) Melyik MSC értesül erről?

Megoldás

MSC_α

c) Mely hálózati elemek értesülnek MS-A2 beszélgetés közbeni hálózaton belüli mozgásáról?

Megoldás

HLR_α, BTS_β, BSC_β, MSC_β, VLR_β

d) A hívás bontása után MS-A2 SMS-t ír MS-A1-nek, aki a tengerbe dobta készülékét. Melyik hálózati elem tárolja az SMS-t annak kézbesítéséig/lejártáig?

Megoldás

SMSC_α

9. feladat

DVB-C rendszerben 64QAM helyett 256QAM-et használunk. 8 MHz-es a raszter, 33,3333%-os lekerekítésű emelt koszinuszos a spektrum.<br\> a) Mekkora a szimbólum- és a bitsebesség? Hány csatorna fér el a rendszerben, ha egy csatorna átlagos sávszélessége 1,5 Mbps?

Megoldás

Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \alpha=\frac{1}{3}} <br\> Szimbólumsebesség: Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle 8 MHz=2*\frac{1}{2T}*(1+\alpha) \Rightarrow \frac{1}{T}=8*10^6*\frac{3}{4}= 6 MBaud} <br\> A 256QAM egy szimbólumban Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \log_{2} 258=8} bitet visz át, a bitsebesség tehát Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle 6 MBaud*8\frac{bit}{szimbolum}=48 Mbps} <br\>

A rendszerben Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{48}{1.5}=32} csatorna fér el.

b) Mik a 6 Mbps sebességű kódoló használatának előnyei ill. hátrányai?

Megoldás

???

c) Mik az előnyei és hátrányai annak, ha 64QAM helyett 1024QAM-et használunk?

Megoldás

• Előny: 6 helyett 10 bit átvitele egy jelzési időn belül, nagyobb bitsebesség.
• Hátrány: nagyobb teljesítményigény.

10. feladat

a) A Kraft-egyenlőtlenség segítségével bizonyítsa be, hogy lehet-e egyértelműen megfejthető kódot készíteni a következő kódszóhosszakkal: 2,2,3,3,3,4,4,4,4!

Megoldás

Ha teljesül a Kraft-egyenlőtlenség: Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \sum_{i=1}^N 2^{-l_i} \leq 1} , ahol l_i az i-edik kódszó hossza, akkor lehet egyértelműen megfejthető kódot készíteni.

Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle 2*\frac{1}{2^{-2}}+3*\frac{1}{2^{-3}}+4*\frac{1}{2^{-4}}=\frac{18}{16} > 1} , tehát nem lehetséges.

b) Készítsen prefixmentes kódot az alábbi kódszóhosszakkal: 2,2,3,3,3,5,5,5,5

Megoldás

Prefixmentes kód: egyik kódszó sem előtagja a másiknak. Jó megoldás például:

• 2 hosszúak:
  • 00
  • 11
• 3 hosszúak:
  • 010
  • 011
  • 100
• 5 hosszúak:
  • 10100
  • 10101
  • 10110
  • 10111