Makroökonómia jelölések

Itt találhatók a Mikmak for dummies I. elején szereplő rövidítések és képletek olvasható és kereshető formában.

← Vissza az előző oldalra – Mikro- és makroökonómia

Jelölések Jel Jelölt mennyiség Q Mennyiségi kibocsátás Y Hozam, jövedelem C Fogyasztás Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \hat{C}} Fogyasztási határhajlandóság C0 Autonóm/jövedelemtől független fogyasztás S Megtakarítás Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \hat{S}} Megtakarítási határhajlandóság I Beruházás i Kamatláb M Pénzmennyiség P Árszínvonal W Nominálbér L k tőke G környezeti beruházás T Adó Tr X export Im import

Képletek Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \hat{C}+\hat{S} = 1<math> * <math>Y = C_0 + \hat{C}(Y-T+T_r) + I + G} - Háromszektoros egyenlet Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle Y = C_0 + \hat{C}Y + I} - Kétszektoros egyenlet Multiplikátorok I. Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{1}{1-\hat{C}} \rightarrow } Adótól független II. Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{1}{1-\hat{C}(1-t)}; (1-t) \rightarrow \text{Jövedelemfüggetlen adó}} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{\DeltaY}{\DeltaG} = \frac{1}{1-\hat{C}}} - ??? Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{\DeltaY}{\DeltaT_r} = \frac{\hat{C}}{1-\hat{C}}} - transzfer Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{\DeltaY}{\DeltaT} = \frac{-\hat{C}}{1-\hat{C}}} - Adó GDP-s dolgok (SNA) 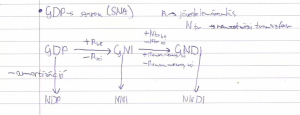Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle GDP = Y = Y + I_B + G + (X - I_m); I_B \rightarrow \text{bruttó beruházás}; (X-I_m) \rightarrow \text{belföldi többlet/nettó export}<\math> <math>NDP = C + I_n + G + (X-I_m)} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle S_k = I_m - X} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle I = S_A + S_k + S_n + S_V} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle T_{rh} + W = C + T_k + S_h} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle Y + T_{rv} = W + T_v + S_v} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle T_{rv} + T_{rh} + S_A + G = T_h + T_v} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \hat{C} + \hat{S} = 1} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle S_0 = -L_0} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle Y + t_{rv} = W + t_v + S_v} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{M}{P} = L^D \rightarrow \text{Lm körbe}} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle T_{rh} + W = C + t_h + S_h} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \mathbf{C = C_0 + \hat{C} \cdot Y}} Értelmezés sikertelen (SVG (a MathML egy böngészőkiegészítővel engedélyezhető): Érvénytelen válasz („Math extension cannot connect to Restbase.”) a(z) https://wikimedia.org/api/rest_v1/ szervertől:): {\displaystyle \frac{M_S}{P} = M^D ; \mathbf{M_0 \cdot \frac{1}{t} = M_S}}