Algoritmuselmélet - PZH, 2013.04.24.

← Vissza az előző oldalra – Algoritmuselmélet

2013.04.24. PZH megoldásai

1. Feladat (Van megoldás)

Egy algoritmus lépésszámáról tudjuk, hogy $T(n)=T\left(\left\lfloor {\frac {n}{4}}\right\rfloor \right)+O(n^{2})$ és tudjuk azt is, hogy $T(1)=T(2)=T(3)=1$. Bizonyítsa be, hogy $T(n)=O(n^{2})$.

Megoldás

Van olyan $c>0$ és $n_{0}$, hogy $n>n_{0}$ esetén $T(n)=T\left(\left\lfloor {\frac {n}{4}}\right\rfloor \right)+O(n^{2})\leq T\left(\left\lfloor {\frac {n}{4}}\right\rfloor \right)+cn^{2}\leq T\left(\left\lfloor {\frac {n}{16}}\right\rfloor \right)+c\left(n^{2}+\left({\frac {n^{2}}{4^{2}}}\right)\right)\leq T\left(\left\lfloor {\frac {n}{64}}\right\rfloor \right)+c\left(n^{2}+\left({\frac {n^{2}}{4^{2}}}\right)+\left({\frac {n^{2}}{16^{2}}}\right)\right)\leq \dots$ $\dots \leq 1+cn^{2}\cdot \left(\sum _{i=0}^{\left\lfloor log_{4}n\right\rfloor }\left({\frac {1}{16}}\right)^{i}\right)$

Azt kell észrevennünk, hogy ez tulajdonképpen egy mértani sor, amire van képletünk:
$\sum _{i=0}^{k}r^{i}={\frac {1-r^{k+1}}{1-r}}$, ahol $k=\left\lfloor log_{4}n\right\rfloor ,r={\frac {1}{16}}$, vagyis ${\frac {1-{\frac {1}{16}}^{\left\lfloor log_{4}n\right\rfloor +1}}{1-{\frac {1}{16}}}}$

${\frac {1-{\frac {1}{16}}^{\left\lfloor log_{4}n\right\rfloor +1}}{1-{\frac {1}{16}}}}<2,$ha $n\geq 1$ (A lényeg, hogy felülről becsüljük!)

Tehát $T(n)=\dots \leq 1+2\cdot cn^{2}=O(n^{2})$

2. Feladat (Van megoldás)

Adott egy teljes bináris fa, a csúcsaiba egész számok vannak írva, összesen n darab (a fa nem feltétlenül bináris keresőfa). Adjon algoritmust, ami $O(n)$ lépésben megkeres egy olyan csúcsot a fában, aminek a részfája kupac, és aminek a magassága a legető legnagyobb az összes ilyen csúcs közül.

Megoldás

Megjegyzések a feladathoz

• Bár nem tartozik a feladathoz, talán érdemes megjegyezzem, hogy bináris kereső fa nem is lehetne, hiszen akkor ott kapásból csak a legalsó szinten lévő elemek lehetnek kupacok (egy 1 elemet tartalmazó kupac), hiszen bináris keresőfánál balra kisebbek, jobbra nagyobbak vannak, míg kupacnál balra és jobbra is nagyobbak vannak.
• Továbbá a teljes bináris fára azért van szükség, mert így "jóval egyszerűbb" a feladat, és nem kell szívózni annak vizsgálatával, hogy az adott részfa teljes bináris fa-e (ugyebár ez a kupac egyik fontos tulajdonsága).

Minden csúcsban 3 adatot fogunk számon tartani: Érték (ez persze adott már), részfa magassága (jelüljük M-mel), és egy bool érték (IGAZ/HAMIS, jelöljük B-vel), hogy igaz-e a részfájára, hogy az kupac.

• Első lépésben a legalsó szinteken lévő csúcsok esetén $M:=1,B:=IGAZ$.
• Legyen egy változónk, amiben tároljuk, hogy melyik csúcsra igaz, hogy a részfája a "legnagyobb" kupac (kezdeti értéke legyen mondjuk az egyik legalsó szinten lévő csúcs).
• Minden további szinten az a feladatunk, hogy megnézzük az adott csúcs (x) bal, és jobb fiát $(JOBB(x),BAL(x))$.
  • Megnézzük, hogy nagyobbak-e, mint x, majd megnézzük, hogy kupac tulajdonsággal bírnak-e:
    • Ha $BAL(x),JOBB(x)>x;BAL(x).B=JOBB(x).B=IGAZ\Rightarrow \Rightarrow x.M:=BAL(x).M+1,x.B:=IGAZ$ majd a változónkba belerakjuk a csúcsot. Vagyis ha mindkettő nagyobb, és mindkettő kupac tulajdonsággal bír, akkor a csúcs részfa magassága 1-gyel nagyobb lesz, mint az egyik (bal, vagy jobb) fia magassága, és kupac tulajdonságú lesz.
    • Ha $BAL(x)<x$ VAGY $JOBB(x)<x$ VAGY $BAL(x).B=HAMIS$ VAGY $JOBB(x).B=HAMIS\Rightarrow \Rightarrow x.M:=BAL(x).M+1,x.B:=HAMIS$. Vagyis ha bármelyik feltétel nem teljesül (valamelyik fia kisebb, avagy valamelyik gyerekére nem igaz, hogy kupac tulajdonságú), akkor maga a csúcs sem lehet már kupac tulajdonságú (itt a magasságot nem is kéne beállítani, de...hát miért is ne).

Mivel minden csúcsot csak egyszer látogatunk meg, így $O(n)$ lépésben megyünk végig a gráfon.

3. Feladat (Van megoldás)

Kukori és Kotkoda egy-egy bináris fára gondolnak (nem feltétlenül bináris keresőfákra). Következik-e, hogy a két fa azonos, ha

(a) inorder bejárással kilolvasva a két fát ugyanazt a számsorozatot kapják?

(b) preorder bejárással kiolvasva a két fát ugyanazt a számsorozatot kapják?

Megoldás

Mindkét esetben 1-1 ellenpéldát kell szolgáltatni:

• a)

Mindkét gráfot A-B-C-D-E sorrendben olvassuk ki, de mégsem egyeznek meg, tehát nem következik.

• b)

Mindkét gráfot F-G-H-J-K sorrendben olvassuk ki, de mégsem egyeznek meg, tehát nem következik.

4. Feladat

TODO

Megoldás

TODO

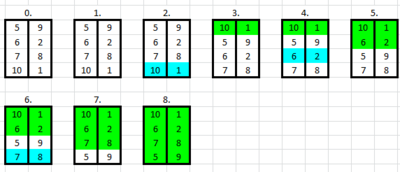
5. Feladat (Van megoldás)

Egy $n$ soros és kettő oszlopos táblázatban adott $n$ számpár (egy sor egy számpárt tartalmaz, a számok mind különböző egész számok a táblázatban). Szeretnénk a táblázat sorait úgy átrendezni, hogy a 2. oszlop szerint növekvő sorrendben legyenek a sorok (számpárok). Egy fajta műveletet hajthatunk végre: kijelölhetünk néhány egymást alatti sort (számpárt) és ezeket rendezhetjük az első oszlop szerint növekvően vagy csökkenően. Adjon algoritmust, ami csak ezt a fajta műveletet használva $O(n)$ lépésben megoldja a feladatot!

Megoldás

• Rendezzük a tömböt az 1. oszlop szerint növekvően.
• A továbbiakban minden $i.$ lépésben megkeressük az $i.$ legkisebb elemet, és a helyére tesszük.
  • Megkeressük a 2. oszlopban az $i.$ legkisebbet, az ő helye a tömbben legyen $k$
  • Mivel az 1. oszlop szerint növekvően vannak a számpárok, így ahhoz, hogy a $k.$ elem az $i.$ helyre kerüljön, a számokat csökkenő sorrendbe kell rendezni az $[i\rightarrow k]$ intervallumon.
  • Ha ezt megcsináltuk, akkor az első $i$ helyen már rendezve lesz a tömb.
  • Az $[i+1\rightarrow n]$ intervallumon rendezzük a számokat növekvő sorrendben.
  • Ezt addig folytatjuk, míg nincs minden számpár a helyén.

• A műveletet minden lépésben $\approx 2n$ alkalommal használjuk:
  • Először növekvő sorrendbe rendeztük az egész tömböt.
  • Utána minden $i.$ lépésben 2x:
    • Egyszer a helyére rakjuk az elemet azzal, hogy csökkenő sorrendbe rakjuk a számpárokat (persze csak a megfelelőket).
    • Majd újra növekvőbe a maradék számpárokat.
• Így az algoritmus $O(n)$ lépéssel rendezi a számpárokat a 2. oszlop szerint.

6. Feladat (Van megoldás)

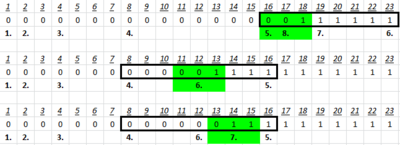
Adott egy $n$ hosszú tömb. Tudjuk, hogy a tömb első néhány ($k$ darab) elem 0, a többi 1, de $k$ értékét nem ismerjük. Adjon $O(logk)$ (nem $O(logn)$ )¹ összehasonlítást használó algoritmust, ami meghatározza $k$ értékét.

¹ A feladatban $O(logk)$ szerepel, de az csak elgépelés.

Megoldás

• Először nézzük meg, hogy az első 2 elem $0-1$-e, ha igen, akkor $k=1$.
• Ha nem, akkor minden további lépésnél ugorjunk a 2x annyiadik cellába (ez legyen $m$), ha pedig túl lépnénk a tömböt ezzel, akkor az utolsóba.
• Vizsgáljuk meg, hogy "hol vagyunk": (az aktuális cellát, és a 2 szomszédját)
  • Ha $0-0-0$-t látunk, akkor ugrunk megint 2x akkorát (ugyanazzal a kritériummal, mint előbb).
  • Ha $0-0-1$-t látunk, akkor $k=m$.
  • Ha $0-1-1$-t látunk, akkor $k=m-1$.
  • Ha $1-1-1$-t látunk, akkor egy bináris keresés segítségével⁽¹⁾ a 2 legutóbbi vizsgált elem közötti cellákban megkeressük a $0-1-1$, vagy $0-0-1$ felállást, és a $k$ értékét a látottak alapján beállítjuk $(k=m-1$ vagy $k=m)$.

⁽¹⁾ Ha $0-0-0$-t lát, jobbra lép, ha $1-1-1$-t, akkor balra, másik 2 esetben pedig találatunk van.

• Az algoritmus működése alapján belátható, hogy $O(logk)$ időben fut.

7. Feladat

TODO

Megoldás

TODO

8. Feladat (Van megoldás)

Bizonyítsa be, hogy egy piros-fekete fában egy levél testvére vagy levél, vagy piros csúcs!

Megoldás

• Összesen 5 felállás lehet:
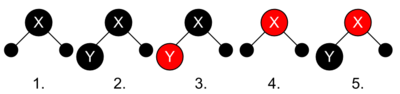
  • Ebből az 1. és a 4. jó is (a 4. persze csak akkor, ha X az nem a főgyökér).
  • A 3. - kis módosítással - látszik, hogy szintén fenn állhat gond nélkül:
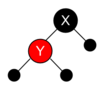
  • Egyedül a 2. és az 5. problémás. Ezek viszont rosszak is, hiszen mindkét esetben elmondható, hogy X-nek a fekete magassága jobbra 1, balra viszont legalább 2, mert az Y csúcsnak legalább 1-1 levél fia van. Tehát belső csúcsnál ilyen állapot nem állhat fent.

• Az első 2 esetben azt bizonyítottuk, hogy levél testvére lehet levél, vagy piros csúcs.
• A 3. esetben pedig azt, hogy nem lehet fekete csúcs a levél testvére.
• Így be is bizonyítottuk, hogy levél testvére CSAK levél, vagy piros csúcs lehet.