„Jelek és jelfeldolgozás kvíz” változatai közötti eltérés
A VIK Wikiből
a (Visszavontam a saját szerkesztésemet (oldid: 205594) – nem ezzel volt a gond) Címke: Visszavonás |
a (Sortörések javítása) |
||
| 37. sor: | 37. sor: | ||
\end{cases}</math> Adja meg a rendszer állapotváltozóinak <math>x(t)</math> közelítő számításához szolgáló előrelépő Euler-séma formuláját!== | \end{cases}</math> Adja meg a rendszer állapotváltozóinak <math>x(t)</math> közelítő számításához szolgáló előrelépő Euler-séma formuláját!== | ||
{{Kvízkérdés|típus=egy|válasz=4}} | {{Kvízkérdés|típus=egy|válasz=4}} | ||
#<math>x(t_k+h_k)\approx(1-h_k)x(t_k)-3h_ku(t_k)</math> | #<math>x(t_k+h_k)\approx(1-h_k)x(t_k)-3h_ku(t_k)</math> | ||
#<math>x(t_k+h_k)\approx(1-2h_k)x(t_k)+3h_ku(t_k)</math> | #<math>x(t_k+h_k)\approx(1-2h_k)x(t_k)+3h_ku(t_k)</math> | ||
| 48. sor: | 47. sor: | ||
\end{cases}</math> Adja meg a rendszer állapotváltozóinak <math>x(t)</math> közelítő számításához szolgáló előrelépő Euler-séma formuláját!== | \end{cases}</math> Adja meg a rendszer állapotváltozóinak <math>x(t)</math> közelítő számításához szolgáló előrelépő Euler-séma formuláját!== | ||
{{Kvízkérdés|típus=egy|válasz=2}} | {{Kvízkérdés|típus=egy|válasz=2}} | ||
#<math>x(t_k+h_k)\approx(1+3h_k)x(t_k)+h_ku(t_k)</math> | #<math>x(t_k+h_k)\approx(1+3h_k)x(t_k)+h_ku(t_k)</math> | ||
#<math>x(t_k+h_k)\approx(1+3h_k)x(t_k)+2h_ku(t_k)</math> | #<math>x(t_k+h_k)\approx(1+3h_k)x(t_k)+2h_ku(t_k)</math> | ||
| 57. sor: | 55. sor: | ||
Jelölje meg az összes tulajdonságot, melyet igaznak tart! | Jelölje meg az összes tulajdonságot, melyet igaznak tart! | ||
{{Kvízkérdés|típus=több|válasz=1,2,4}} | {{Kvízkérdés|típus=több|válasz=1,2,4}} | ||
#invariáns | #invariáns | ||
#kauzális | #kauzális | ||
| 66. sor: | 63. sor: | ||
Jelölje meg az összes tulajdonságot, melyet igaznak tart! | Jelölje meg az összes tulajdonságot, melyet igaznak tart! | ||
{{Kvízkérdés|típus=több|válasz=1,3,4}} | {{Kvízkérdés|típus=több|válasz=1,3,4}} | ||
#invariáns | #invariáns | ||
#kauzális | #kauzális | ||
| 73. sor: | 69. sor: | ||
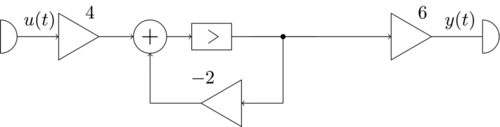
==Az alábbi ábrán látható egy folytonos idejű rendszert reprezentáló jelfolyamhálózat. Adja meg a rendszer állapotváltozós leírásának normálalakját!== | ==Az alábbi ábrán látható egy folytonos idejű rendszert reprezentáló jelfolyamhálózat. Adja meg a rendszer állapotváltozós leírásának normálalakját!== | ||
[[Fájl:Jelek_20240424_ZH_jelfolyamhálózat.png|keret|keretnélküli|500x500px]]{{Kvízkérdés|típus=egy|válasz=4}} | [[Fájl:Jelek_20240424_ZH_jelfolyamhálózat.png|keret|keretnélküli|500x500px]] | ||
{{Kvízkérdés|típus=egy|válasz=4}} | |||
#<math>\begin{cases} | #<math>\begin{cases} | ||
x'(t)=4x(t)+2u(t) \\ | x'(t)=4x(t)+2u(t) \\ | ||
| 94. sor: | 90. sor: | ||
==Egy diszkrét idejű rendszer ugrásválasza <math>g[k]=\varepsilon[k]2^k</math>. Adja meg a rendszer <math>h[k]</math> impulzusválaszát!== | ==Egy diszkrét idejű rendszer ugrásválasza <math>g[k]=\varepsilon[k]2^k</math>. Adja meg a rendszer <math>h[k]</math> impulzusválaszát!== | ||
{{Kvízkérdés|típus=egy|válasz=3}} | {{Kvízkérdés|típus=egy|válasz=3}} | ||
#<math>\frac{1}{2}\delta[k]</math> | #<math>\frac{1}{2}\delta[k]</math> | ||
#<math>\frac{1}{2}\varepsilon[k]2^k</math> | #<math>\frac{1}{2}\varepsilon[k]2^k</math> | ||
| 103. sor: | 98. sor: | ||
==Egy diszkrét idejű rendszer rendszeregyenlete <math>y[k]+5y[k-1]=u[k]-2u[k-1]</math>. Adja meg a rendszer átviteli karakterisztikáját!== | ==Egy diszkrét idejű rendszer rendszeregyenlete <math>y[k]+5y[k-1]=u[k]-2u[k-1]</math>. Adja meg a rendszer átviteli karakterisztikáját!== | ||
{{Kvízkérdés|típus=egy|válasz=3}} | {{Kvízkérdés|típus=egy|válasz=3}} | ||
#<math>H(e^{j\vartheta})=\frac{-1+2e^{-j\vartheta}}{1+5e^{-j\vartheta}}</math> | #<math>H(e^{j\vartheta})=\frac{-1+2e^{-j\vartheta}}{1+5e^{-j\vartheta}}</math> | ||
#Nem létezik | #Nem létezik | ||
| 113. sor: | 107. sor: | ||
A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező. | A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező. | ||
{{Kvízkérdés|típus=egy|válasz=3}} | {{Kvízkérdés|típus=egy|válasz=3}} | ||
#3 | #3 | ||
#4 | #4 | ||
| 122. sor: | 115. sor: | ||
A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező. | A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező. | ||
{{Kvízkérdés|típus=egy|válasz=2}} | {{Kvízkérdés|típus=egy|válasz=2}} | ||
#3 | #3 | ||
#4 | #4 | ||
| 130. sor: | 122. sor: | ||
==Egy diszkrét idejű, lineáris, invariáns rendszer ugrásválasza <math>y[k]=5\cdot0,8^k\varepsilon[k]</math>. Adja meg a rendszer válaszát az <math>u[k]=2\cdot\varepsilon[k+3]</math> gerjesztésre!== | ==Egy diszkrét idejű, lineáris, invariáns rendszer ugrásválasza <math>y[k]=5\cdot0,8^k\varepsilon[k]</math>. Adja meg a rendszer válaszát az <math>u[k]=2\cdot\varepsilon[k+3]</math> gerjesztésre!== | ||
{{Kvízkérdés|típus=egy|válasz=3}} | {{Kvízkérdés|típus=egy|válasz=3}} | ||
#<math>5\cdot0,8^{k+3}\varepsilon[k+3]</math> | #<math>5\cdot0,8^{k+3}\varepsilon[k+3]</math> | ||
#Az <math>u[k]</math> nem belépő, ezért nem létezik | #Az <math>u[k]</math> nem belépő, ezért nem létezik | ||
| 139. sor: | 130. sor: | ||
==Egy diszkrét idejű jel időfüggvénye <math>x[k]=2\cos[0,25\pi k-1,25]</math>. Adja meg a jel fazorát (komplex csúcsértékét)!== | ==Egy diszkrét idejű jel időfüggvénye <math>x[k]=2\cos[0,25\pi k-1,25]</math>. Adja meg a jel fazorát (komplex csúcsértékét)!== | ||
{{Kvízkérdés|típus=egy|válasz=4}} | {{Kvízkérdés|típus=egy|válasz=4}} | ||
#<math>\bar X=2e^{j0,25}</math> | #<math>\bar X=2e^{j0,25}</math> | ||
#<math>\bar X=2e^{j1,25}</math> | #<math>\bar X=2e^{j1,25}</math> | ||
#<math>\bar X=2e^{-j0,25}</math> | #<math>\bar X=2e^{-j0,25}</math> | ||
#<math>\bar X=2e^{-j1,25}</math> | #<math>\bar X=2e^{-j1,25}</math> | ||
==Egy diszkrét idejű jel időfüggvénye <math>x[k]=5\cos[0,5\pi k-0,5]</math>. Adja meg a jel fazorát (komplex csúcsértékét)!== | ==Egy diszkrét idejű jel időfüggvénye <math>x[k]=5\cos[0,5\pi k-0,5]</math>. Adja meg a jel fazorát (komplex csúcsértékét)!== | ||
{{Kvízkérdés|típus=egy|válasz=3}} | {{Kvízkérdés|típus=egy|válasz=3}} | ||
#<math>\bar X=5e^{j0,5}</math> | #<math>\bar X=5e^{j0,5}</math> | ||
#<math>\bar X=0,5e^{j0,5}</math> | #<math>\bar X=0,5e^{j0,5}</math> | ||
#<math>\bar X=5e^{-j0,5}</math> | #<math>\bar X=5e^{-j0,5}</math> | ||
#<math>\bar X=0,5e^{-j0,05}</math> | #<math>\bar X=0,5e^{-j0,05}</math> | ||
A lap 2024. június 5., 20:41-kori változata
A csillaggal jelölt kérdések csak a vizsgán várhatóak.
Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza . Gerjesztés-válasz stabilis-e a rendszer?
- Nem, mert az impulzusválaszban szerepel a .
- Igen, mert az impulzusválasz belépő.
- Igen, mert az impulzusválasz abszolút integrálható.
- Nem, mert az impulzusválasz nem abszolút integrálható.
- Igen, mert az impulzusválaszban szereplő és együtthatója azonos nagyságú és ellentétes előjelű.
Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza . Gerjesztés-válasz stabilis-e a rendszer?
- Nem, mert az impulzusválaszban szerepel a .
- Igen, mert az impulzusválasz belépő.
- Igen, mert az impulzusválasz abszolút integrálható.
- Nem, mert az impulzusválasz nem abszolút integrálható.
- Igen, mert az impulzusválaszban szereplő és együtthatója azonos nagyságú és ellentétes előjelű.
Egy folytonos idejű rendszer impulzusválasza . Adja meg a rendszer ugrásválaszát!
- Nem létezik
Adott egy elsőrendű, folytonos idejű lineáris invariáns rendszer állapotváltozós leírásának normálalakja: Adja meg a rendszer állapotváltozóinak közelítő számításához szolgáló előrelépő Euler-séma formuláját!
Adott egy elsőrendű, folytonos idejű lineáris invariáns rendszer állapotváltozós leírásának normálalakja: Adja meg a rendszer állapotváltozóinak közelítő számításához szolgáló előrelépő Euler-séma formuláját!
Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: . Jellemezze a rendszert!
![{\displaystyle y(t)=5[u(t)]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5147ee900b30c5e0709a9fd86325a9c030580519)
Jelölje meg az összes tulajdonságot, melyet igaznak tart!
- invariáns
- kauzális
- lineáris
- gerjesztés-válasz stabil
Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: . Jellemezze a rendszert!
![{\displaystyle y(t)=5[u(t+3)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d41e671a0c9a00eba015d7657d66b4d968bbd8a)
Jelölje meg az összes tulajdonságot, melyet igaznak tart!
- invariáns
- kauzális
- lineáris
- gerjesztés-válasz stabil
Az alábbi ábrán látható egy folytonos idejű rendszert reprezentáló jelfolyamhálózat. Adja meg a rendszer állapotváltozós leírásának normálalakját!
Egy diszkrét idejű rendszer ugrásválasza . Adja meg a rendszer impulzusválaszát!
![{\displaystyle g[k]=\varepsilon [k]2^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fcdb86d62c75ff1d16ba223a92e753d04e7b120)
![{\displaystyle h[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e944606b94261ca96a82ff41b4b8aade7ff14acc)
- Nem létezik
![{\displaystyle {\frac {1}{2}}\delta [k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc847929f61f8ba98a016787696aa42df096714a)
![{\displaystyle {\frac {1}{2}}\varepsilon [k]2^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b32fe105a6a89eb2abd2612b0a82f0a80ad8df19)
![{\displaystyle {\frac {1}{2}}\delta [k]+{\frac {1}{2}}\varepsilon [k]2^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48e0365bf729610806d6bb31c5af0873ed233b23)
![{\displaystyle \delta [k]+\varepsilon [k]2^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b4bbb9ec8fe4bbd862c39a7aca7c04ab43fd850)
Egy diszkrét idejű rendszer rendszeregyenlete . Adja meg a rendszer átviteli karakterisztikáját!
![{\displaystyle y[k]+5y[k-1]=u[k]-2u[k-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e67d6f2ab82b574a2eb01bc59768932a3a9dbd7)
- Nem létezik
Egy diszkrét idejű jel időfüggénye a . Állapítsa meg a jel periódushosszát!
![{\displaystyle x[k]=\cos[0,4\pi k+4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e322b5206345acd388c554972636ab8d431042e9)
A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.
- 3
- 4
- 5
- 6
Egy diszkrét idejű jel időfüggénye a . Állapítsa meg a jel periódushosszát!
![{\displaystyle x[k]=\cos[0,75\pi k+4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a27e81988f739fe209575b547cef793bbae7e106)
A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.
- 3
- 4
- 5
- 6
Egy diszkrét idejű, lineáris, invariáns rendszer ugrásválasza . Adja meg a rendszer válaszát az gerjesztésre!
![{\displaystyle y[k]=5\cdot 0,8^{k}\varepsilon [k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/865b3dd8a0f721d5200583e78dfc1eeda54513c7)
![{\displaystyle u[k]=2\cdot \varepsilon [k+3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddaa6f47b1ee9d5f5894dc8481e8d04c02ad5b65)
- Az nem belépő, ezért nem létezik
![{\displaystyle 5\cdot 0,8^{k+3}\varepsilon [k+3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2b0ad943f5c46064492c795be47ba7692a444c9)
![{\displaystyle u[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fdeceffda4e9932b27b66ad7f7e1ddf8a831df3)
![{\displaystyle 10\cdot 0,8^{k+3}\varepsilon [k+3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1926b606f7fdf4676bdfc59ae1971cb1bae67d57)
![{\displaystyle 10\cdot 0,8^{k-3}\varepsilon [k-3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebf8284523a2ca5d5df5c9f9458649513529580d)
![{\displaystyle 5\cdot 0,8^{k-3}\varepsilon [k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57d4e391751bf67f136edba7b60d022260e6611f)
Egy diszkrét idejű jel időfüggvénye . Adja meg a jel fazorát (komplex csúcsértékét)!
![{\displaystyle x[k]=2\cos[0,25\pi k-1,25]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd1c68db161c7de8d43a5162cf1f316e63020475)
Egy diszkrét idejű jel időfüggvénye . Adja meg a jel fazorát (komplex csúcsértékét)!
![{\displaystyle x[k]=5\cos[0,5\pi k-0,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faaf01728b67676bbeedcf4366110abfaf482a35)
