„Záróvizsga kvíz - Algoritmusok” változatai közötti eltérés
kérdések hozzáadása |
kérdések hozzáadása |
||
| 29. sor: | 29. sor: | ||
# <math>\left(\begin{array}{c}2 n-3 \\ n\end{array}\right)</math> | # <math>\left(\begin{array}{c}2 n-3 \\ n\end{array}\right)</math> | ||
# <math>\left(\begin{array}{c}2 n \\ n\end{array}\right) \cdot \frac{1}{3 !}</math> | # <math>\left(\begin{array}{c}2 n \\ n\end{array}\right) \cdot \frac{1}{3 !}</math> | ||
== Pozitív egész számokat szeretnénk tárolni valami adatszerkezet segítségével úgy, hogy <math>n</math> tárolt elem esetén tetszőleges <math>x</math> egész számról <math>O(\log n)</math> lépésben meg tudjuk mondani, hogy igaz-e rá, hogy <math>x</math> a tárolt számok között van, de sem <math>x-1</math>, sem <math>x+1</math> nincsen. (2022 jun) == | |||
Melyik adatszerkezettel valósítható ez meg? | |||
{{Kvízkérdés|típus=egy|válasz=1}} | |||
# 2-3 fa | |||
# rendezett lista | |||
# nyílt címzésú hash | |||
# (nem feltétlenül kiegyensúlyozott) bináris keresőfa | |||
== Az 1, 8, 10,12, 20, 27, 30 rendezett tömbben bináris kereséssel keressük a 30-at. Hány összehasonlítás után találjuk meg? (2022 jun) == | |||
{{Kvízkérdés|típus=egy|válasz=4}} | |||
# 2 | |||
# 1 | |||
# 7 | |||
# 3 | |||
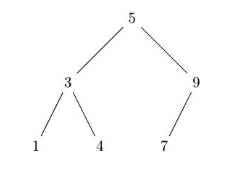
== Egy kezdetben üres bináris keresőfába szúrtunk be elemeket (törlés nem volt). Az alábbiak közül melyik beszúrási sorrend eredményezi az ábrán látható fát? (2022 jun) == | |||
[[Fájl:2022 jun info zv adatb fagraf.png|keretnélküli]] | |||
{{Kvízkérdés|típus=egy|válasz=3}} | |||
# <math>5,9,1,7,3,4</math> | |||
# <math>5,7,4,9,3,1</math> | |||
# <math>5,3,4,9,1,7</math> | |||
# <math>5,4,7,3,9,1</math> | |||
== Tekintsük azt a feladatot, ahol egy <math>n>100</math> csúcsú irányított <math>G</math> gráfról azt szeretnénk eldönteni, hogy van-e 100 olyan csúcsa, hogy a gráfból ezeket elhagyva a maradék gráf csupa izolált pontból áll. (2022 jun) == | |||
Melyik állítás igaz az alábbiak közül, ha feltesszük, hogy <math>P \neq N P</math> ? | |||
{{Kvízkérdés|típus=egy|válasz=4}} | |||
# A probléma <math>P</math>-ben van, de nincs <math>N P</math>-ben. | |||
# A probléma <math>N P</math>-teljes és nincs <math>P</math>-ben. | |||
# A probléma <math>P</math>-ben van és <math>N P</math>-teljes. | |||
# A probléma <math>P</math>-ben és <math>N P</math>-ben is benne van. | |||
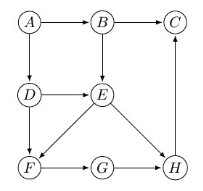
== A megadottak közül melyik egy topologikus sorrendje az ábrán látható gráfnak? (2022 jun) == | |||
[[Fájl:2022 jun info zv algoritmusok graf.png|keretnélküli]] | |||
{{Kvízkérdés|típus=egy|válasz=1}} | |||
# <math>A, B, D, E, F, G, H, C</math> | |||
# <math>A, D, F, G, H, C, E, B</math> | |||
# <math>A, B, C, D, E, F, G, H</math> | |||
# <math>A, D, F, E, B, G, H, C</math> | |||
== Egy <math>n \times n</math>-es táblázat mezőin akarunk eljutni a bal felső cellából az utolsó sorba (itt mindegy, hogy a soron belül melyik oszlopba érkezünk). (2022 jun) == | == Egy <math>n \times n</math>-es táblázat mezőin akarunk eljutni a bal felső cellából az utolsó sorba (itt mindegy, hogy a soron belül melyik oszlopba érkezünk). (2022 jun) == | ||
A szabályok a következők: | A szabályok a következők: | ||
# Az első oszlop első mezőjéről kell indulnunk és a végén az utolsó sor tetszőleges mezőjére kell érkeznünk. | |||
# Egy lépésben vagy egy cellát mehetünk lefele (és maradunk ugyanabban az oszlopban) vagy egy cellát megyünk jobbra (és maradunk ugyanabban a sorban) vagy átlósan lépünk egyet lefele jobbra (azaz egy sort lefele és egy oszlopnyit jobbra). | |||
Jelölje <math>T[i, j](1 \leq i, j \leq n</math> esetén) azt, hogy az <math>i</math>-edik sor <math>j</math>-edik oszlopában levő mezőbe hányféleképpen juthatok el a bal felső cellából. | Jelölje <math>T[i, j](1 \leq i, j \leq n</math> esetén) azt, hogy az <math>i</math>-edik sor <math>j</math>-edik oszlopában levő mezőbe hányféleképpen juthatok el a bal felső cellából. | ||
Inicializáljuk a kezdeti értékeket így: mivel az első sor minden cellájába egyféleképpen juthatunk, ezért <math>T[1, j]=1</math> minden <math>1 \leq j \leq n</math> esetén és hasonlóan, mivel az első oszlop minden cellájába is egy út vezet, ezért <math>T[i, 1]=1</math> minden <math>1 \leq i \leq n</math> esetén. | Inicializáljuk a kezdeti értékeket így: mivel az első sor minden cellájába egyféleképpen juthatunk, ezért <math>T[1, j]=1</math> minden <math>1 \leq j \leq n</math> esetén és hasonlóan, mivel az első oszlop minden cellájába is egy út vezet, ezért <math>T[i, 1]=1</math> minden <math>1 \leq i \leq n</math> esetén. | ||
A lap 2023. december 11., 22:51-kori változata
Az 1, 8, 10,12, 20, 27, 30 rendezett tömbben bináris kereséssel keressük a 30-at. Hány összehasonlítás után találjuk meg? (2022 jun)
- 2
- 1
- 7
- 3
A hátizsák feladatra tanult dinamikus programozást használó algoritmust futtatjuk -es hátizsák kapacitással. A táblázat -es sora az értékekkel így néz ki: (2022 jan)
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 0 | 0 | 7 | 7 | 8 | 12 | 12 | 12 | 12 | 20 | 20 |
Mi igaz a következő, -as sor értékeire az alábbiak közül, ha a 8. tárgy súlya , értéke pedig ? ( jelentése: az első tárgyból hátizsák kapacitás mellett elérhető maximális érték.)
A tömböt rendezzük öszefésüléses rendezéssel. Hány összehasonlítás történik a rendezés teljes futása alatt? (2022 jan)
- 12
- 7
- 4
- 8
Egy irányítatlan nyolc csúcsú gráfon DFS-t (mélységi bejárást) futtatunk úgy, hogy ha döntési helyzetben vagyunk, akkor az ábécé szerinti sorrend szerint haladunk. A DFS fába az alábbi élek kerülnek be ebben a sorrendben: . Mi igaz a csúcs fokszámára az alábbiak közül? (2022 jan)
- fokszáma lehet 1 vagy 2, és más nem lehet
- fokszáma lehet 1, 2, 3 vagy 4, és más nem lehet
- fokszáma lehet 1, 2 vagy 3, és más nem lehet
- fokszáma lehet 1, 2, 3, 4 vagy 5, és más nem lehet
Egy -es táblázat mezőin akarunk eljutni a bal felső cellából az utolsó sorba (itt mindegy, hogy a soron belül melyik oszlopba érkezünk). (2022 jun)
A szabályok a következők:
- Az első oszlop első mezőjéről kell indulnunk és a végén az utolsó sor tetszőleges mezőjére kell érkeznünk.
- Egy lépésben vagy egy cellát mehetünk lefele (és maradunk ugyanabban az oszlopban) vagy egy cellát megyünk jobbra (és maradunk ugyanabban a sorban) vagy átlósan lépünk egyet lefele jobbra (azaz egy sort lefele és egy oszlopnyit jobbra).
Jelölje esetén) azt, hogy az -edik sor -edik oszlopában levő mezőbe hányféleképpen juthatok el a bal felső cellából. Inicializáljuk a kezdeti értékeket így: mivel az első sor minden cellájába egyféleképpen juthatunk, ezért minden esetén és hasonlóan, mivel az első oszlop minden cellájába is egy út vezet, ezért minden esetén. Melyik rekurziós képlet a helyes a többi érték meghatározására?
Az előző feladat folytatása:
A teljesen kitöltött táblázat segítségével hogyan kaphatjuk meg azt, hogy hányféleképpen lehet eljutni a bal felső cellából a legalsó sorba?
- adja meg ezt.
- adja meg ezt.
- adja meg ezt.
- adja meg ezt
- adja meg ezt.
Egy kezdetben üres bináris keresőfába beszúrtuk az egész számokat valamilyen sorrendben (a sorrend nem ismert). Mi igaz biztosan az alábbiak közül? (2022 jan)
- Az 1 levélben van.
- A fának 7 szintje van.
- A legutoljára beszúrt érték levélben van.
- A középső érték, azaz a 64, a gyökérben van.
Tekintsük az alábbi két függvényt (itt a log függvény kettes alapú logaritmust jelöl): (2023 jun)
Az alábbiak közül melyik állítás igaz?
- , mert mindkét függvényre igaz, hogy
- , mert és
- , de az előző két indoklás egyike sem helyes
Legyen a Értelmezés sikertelen (formai hiba): {\displaystyle 2SZÍN} eldöntési probléma, azaz ahol egy egyszerü, irányítatlan gráfról azt szeretnénk eldönteni, hogy ki lehet-e színezni a csúcsait két színnel úgy, hogy azonos színú csúcsok közőtt ne menjen él. Az eldöntési problémában pedig azt kell eldöntenünk darab pozitív egész számról, hogy van-e ezeknek a számoknak egy olyan részhalmaza, hogy a részhalmazban levő számok összege megegyezik a részhalmazba be nem vett számok összegével. (2022 jun)
Mi igaz az alábbiak közül, ha feltételezzük, hogy ?
- nem Karp-redukálható -ra, de Karp-redukálható -re.
- Karp-redukálható -ra és is Karp-redukálható -re.
- sem Karp-redukálható -ra és sem Karp-redukálható -re.
- Karp-redukálható -ra, de nem Karp-redukálható -re.
Tekintsük az alábbi három függvényt (itt a függvény mindig kettes alapú logaritmust jelöl): (2022 jan)
Az alábbiak közül melyik állítás igaz ezen három függvény nagyságrendjére?
- és
- és
- és
- és
Adott egy csúcsú teljes gráf, a csúcsok számozottak, az 1, 2,…, n számozású csúcsok pirosra vannak színezve, a többi csúcs színtelen. Hány olyan különböző Hamilton-út van a gráfban, amelyben az első n csúcs piros? (2022 jan)
Radix rendezéssel rendezünk 5 hosszú karaktersorozatokat, ahol a karakterek mindegyik pozícióban a 4-elemű ábécéből kerülnek ki. Mi igaz ekkor a radix rendezés során használt ládarendezésekre? (2022 jan)
- 1 ládarendezést használunk ládával.
- 5 ládarendezést használunk, mindegyik esetben 4 ládával.
- 4 ládarendezést használunk, mindegyik esetben 5 ládával.
- 1 ládarendezést használunk 20 ládával.
Egy bináris keresőfa preorder bejárása a csúcsokat sorrendben látogatja meg. (2023 jun)
Melyik igaz az alábbi állítások közül a keresőfára?
- A 7 a 12 egyik részfájában van.
- A 8 a gyökérben van.
- A 10 a 2 egyik részfájában van.
- A 2 egy levélben van.
Pozitív egész számokat szeretnénk tárolni valami adatszerkezet segítségével úgy, hogy tárolt elem esetén tetszőleges egész számról lépésben meg tudjuk mondani, hogy igaz-e rá, hogy a tárolt számok között van, de sem , sem nincsen. (2022 jun)
Melyik adatszerkezettel valósítható ez meg?
- 2-3 fa
- rendezett lista
- nyílt címzésú hash
- (nem feltétlenül kiegyensúlyozott) bináris keresőfa
darab különböző csokiból hányféleképpen tudunk kiválasztani darabot úgy, hogy a három kedvenc csokink a kiválasztottak között legyen? (2023 jun)
Legyen az az eldöntési probléma, ahol egy irányítatlan páros gráfról és egy számról azt szeretnénk eldönteni, hogy van-e -ben élű párosítás és legyen az a kérdés, ahol egy irányítatlan gráfról és egy számról azt szeretnénk eldönteni, hogy van-e -ben pontból álló klikk (azaz teljes gráf). (2022 jan)
Mi igaz az alábbiak közül, ha feltételezzük, hogy ?
- Karp-redukálható -ra, de nem Karp-redukálható -re.
- nem Karp-redukálható -ra, de Karp-redukálható -re.
- Karp-redukálható -ra és is Karp-redukálható -re.
- sem Karp-redukálható -ra és sem Karp-redukálható -re.
Tekintsük azt a feladatot, ahol egy csúcsú irányított gráfról azt szeretnénk eldönteni, hogy van-e 100 olyan csúcsa, hogy a gráfból ezeket elhagyva a maradék gráf csupa izolált pontból áll. (2022 jun)
Melyik állítás igaz az alábbiak közül, ha feltesszük, hogy ?
- A probléma -ben van, de nincs -ben.
- A probléma -teljes és nincs -ben.
- A probléma -ben van és -teljes.
- A probléma -ben és -ben is benne van.
A egyszerű, irányítatlan gráf élei súlyozottak. Tegyük fel, hogy az élek súlyai különbözőek és hogy van legalább három éle a gráfnak. (2022 jun)
Tekintsük a következő állításokat: A: minden minimális feszítőfája tartalmazza a legkisebb súlyú élt. B: minden minimális feszítőfája tartalmazza a második legkisebb súlyú élt. C: egyik minimális feszítőfája sem tartalmazza a legnagyobb súlyú élt. Melyik a helyes az alábbi lehetőségek közül?
- Csak az állítás igaz, a másik kettő nem
- Az , a és a állítás is igaz.
- Csak az és a állítás igaz, a nem.
- Csak az és a állítás igaz, a nem.
Az algoritmusról tudjuk, hogy lépésszáma a bemenet hosszának, -nek a függvényében . (2022 jun)
Melyik nem igaz az alábbiak közül?
- Minden pozitív számhoz lehet olyan hosszú bemenet, amelyiken lépésszáma kisebb, mint .
- Minden pozitív számhoz lehet olyan hosszú bemenet, amelyiken lépésszáma nagyobb, mint .
- Minden pozitív számhoz lehet olyan hosszú bemenet, amelyiken lépésszáma kisebb, mint .
- Minden pozitív számhoz lehet olyan hosszú bemenet, amelyiken lépésszáma nagyobb, mint .
Egy csupa különböző egész számot tartalmazó bináris keresőfában egy keresés során az alábbi értékeket látjuk (x értéke nem ismert): . Az alábbiak közül mi igaz x értékére? (2022 jan)
- x lehet 1 is és 9 is
- x lehet 6 is és 9 is
- x lehet 1 is és 6 is
- x lehet 2 is és 12 is
Egy kezdetben üres bináris keresőfába szúrtunk be elemeket (törlés nem volt). Az alábbiak közül melyik beszúrási sorrend eredményezi az ábrán látható fát? (2022 jun)
Az tömböt rendezzük a szokásos (módosítás nélkül futtatott) öszefésüléses rendezéssel. Hány összehasonlítás történik a rendezés teljes futása alatt? (2022 jun)
- 0
- 64
- 32
Tekintsük azt a teljes páros gráfot, melynek és a két osztálya. Hány maximális (azaz tovább nem bővíthető) párosítás van ebben a gráfban? (Két párosítás különböző, ha nem pontosan ugyanazokból az élekből áll.) (2022 jun)
- !
Tekintsük azt az eldöntési feladatot, ahol egy irányított gráfról azt szeretnénk eldönteni, hogy van-e két olyan és csúcsa, hogy -ből van irányított út -be, de -ből nincsen irányított út -be (2022 jan)
Melyik állítás igaz az alábbiak közül, ha feltesszük, hogy ?
- A probléma -ben és -ben is benne van.
- A probléma -ben van, de nincs -ben.
- A probléma -teljes és nincs -ben.
- A probléma -ben van és -teljes.