|
|
| 100. sor: |
100. sor: |
|
| |
|
|
| |
|
| * <math>Y = C_0 + \hat{C}(Y-T+T_r) + I + G</math> - Háromszektoros egyenlet | | * <math>Y = C_0 + \hat{C}(Y+TR - T) + I + G</math> - Háromszektoros egyenlet |
| | * <math>T = T_0 - z \cdot Y</math> |
| | * <math>I = I_0 - a \cdot r</math> |
| * <math>Y = C_0 + \hat{C}Y + I</math> - Kétszektoros egyenlet | | * <math>Y = C_0 + \hat{C}Y + I</math> - Kétszektoros egyenlet |
| * Multiplikátorok | | * Multiplikátorok |
| # <math>\frac{1}{1-\hat{C}} \rightarrow </math> Adótól független | | # <math>\frac{1}{1-\hat{C}} \rightarrow </math> Adótól független |
| # <math>\frac{1}{1-\hat{C}(1-t)}; (1-t) \rightarrow \text{Jövedelemfüggetlen adó}</math> | | # <math>\frac{1}{1-\hat{C}(1-z)} \rightarrow \text{Adókulccsal bőcített kiadási multiplikátor}</math> |
|
| |
|
|
| |
|
| * <math>\frac{\Delta Y}{\Delta G} = \frac{1}{1-\hat{C}}</math> - '''???''' | | * Kormányzati kereslet multiplikátora: <math>\frac{\Delta Y}{\Delta G} \text{ vagy } \frac{\Delta Y}{\Delta C_0} \text{ vagy } \frac{\Delta Y}{\Delta I_0} = \frac{1}{1-\hat{C}(1-z)}</math> |
| * <math>\frac{\Delta Y}{\Delta T_r} = \frac{\hat{C}}{1-\hat{C}}</math> - transzfer | | * Transzfer multiplikátora: <math>\frac{\Delta Y}{\Delta T_r} = \frac{\hat{C}}{1-\hat{C}(1-z)}</math> |
| * <math>\frac{\Delta Y}{\Delta T} = \frac{-\hat{C}}{1-\hat{C}}</math> - Adó | | * Autonóm adó multiplikátora: <math>\frac{\Delta Y}{\Delta T} = \frac{-\hat{C}}{1-\hat{C}(1-z)}</math> |
| | |
| | Haavelmo-tétel: <math>z = 0 \text{, és csak } T_0 \text{ van}</math> |
| | |
| | Tétel: <math> \Delta G = \Delta T \Rightarrow \Delta Y = \Delta G </math> |
|
| |
|
| * GDP-s dolgok (SNA) | | * GDP-s dolgok (SNA) |
A lap 2017. december 2., 13:14-kori változata
Itt találhatók a Mikmak for dummies I. elején szereplő rövidítések és képletek olvasható és kereshető formában.
Jelölések
| Jel |
Jelölt mennyiség
|
| Q |
Mennyiségi kibocsátás
|
| Y |
Hozam, jövedelem
|
| YDIS |
Rendelkezésre álló jövedelem
|
| C |
Fogyasztás
|
|
Fogyasztási határhajlandóság
|
| C0 |
Autonóm/jövedelemtől független fogyasztás
|
| S |
Megtakarítás/Elszivárgás
|
| S0 |
Autonóm megtakarítás
|
|
Megtakarítási határhajlandóság
|
| I |
Beruházás
|
| IB |
Bruttó beruházás
|
| In |
|
| r |
Kamatláb
|
| a |
Kamatérzékenység
|
| M |
(Minimális) Pénzmennyiség
|
| P |
Árszínvonal
|
| W |
Nominálbér (pénzben kifejezett munkabér)
|
| L |
|
| LD |
pénzkereseti függvény
|
| k |
tőke
|
| G |
környezeti beruházás/állami kiadások
|
| T |
Adó
|
| T0 |
Autonóm adó
|
| Tr |
Transzfer juttatások (ellenszolgáltatás nélküli)
|
| X |
export
|
| Im |
import
|
| GDP |
bruttó hazai termék (gross domestic product)
|
| NDP |
|
| GNI |
gross national income
|
| MNI |
|
| GNDI |
|
| NNDI |
|
| R |
jövedelemáramlás
|
| GO |
A nemzetgazdaság adott évi összes megtermelt java, másnéven bruttó kibocsátás
|
| BB |
Költségvetés
|
| z |
Jövedelemfüggő adókulcs
|
|
Képletek
- Jövedelemfüggő adó
- - Háromszektoros egyenlet
- - Kétszektoros egyenlet
- Multiplikátorok
- Adótól független
- Kormányzati kereslet multiplikátora:
- Transzfer multiplikátora:
- Autonóm adó multiplikátora:
Haavelmo-tétel:
Tétel:
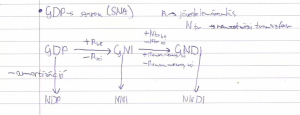
- Árupiac:
- Reál GDP:
- Értelmezés sikertelen (formai hiba): {\displaystyle NNI = GNI - amortizáció}
- Háztartás:
- Vállalat:
- Állam:
- Külföld:
- Tőkepiac: Értelmezés sikertelen (formai hiba): {\displaystyle I = S_Á + S_k + S_h + S_V}
|

