Számítógépes látórendszerek - Ellenőrző kérdések: Mérések

← Vissza az előző oldalra – Számítógépes látórendszerek

Hogyan definiálhatjuk egy objektum pozícióját?
Ismertesse a pozíciómérés lehetőségeit.
Mutassa meg, hogy lehet a pozíció értékét meghatározni bináris és maszkolt szürkeárnyalatos képeken.

Egy 2D-s képet ábrázolhatunk egy derékszögű koordinátarendszerben, ahol az egyes pixelekhez hozzárendelhetünk egy (x,y) egész koordinátapárt. A koordinátarendszer középpontja tetszőlegesen, feladattól függően megválasztható, de általában a bal felső sarokban lévő pixelhez rendeljük hozzá a (0,0)-t. Egy objektum pozíciója az objektum egy jellegzetes koordinátapárjával jellemezhető. Ez a koordinátapár lehet: geometriai középpont – az objektumot befoglaló téglalap/kör középpontja tömegközéppont

Tömegközéppont $(x_{c},y_{c})$ meghatározása

A kép mérete: $M\cdot N$ pixel

• $p_{x}(x)=$ az $x$ koordinátájú sorban a vizsgált objektum pixeleinek száma
• $p_{y}(y)=$ az $y$ koordinátájú oszlopban a vizsgált objektum pixeleinek száma

Szürkeárnyalatos képekre

$I(x,y)$: intenzitásfüggvény

Geometriai középpont $(x_{g},y_{g})$ meghatározása

$x_{min},x_{max},y_{min},y_{max}$ : az objektum legszélső pixeleinek koordinátái

Hogyan definiálhatjuk egy objektum orientációját?
Sorolja fel az orientációmérés lehetőségeit, illetve röviden ismertesse ezek alapelvét.

Objektum orientációján egy objektum egy olyan 1D-s jellemzését értjük, mely irány-, szöginformációkat szolgáltat az adott objektumról. Objektum orientációja megadható a

• befoglaló téglalap arányaival és méreteivel
• legnagyobb távolsággal az objektumon belül
• középponttól vett legnagyobb távolsággal
• rá illeszthető legkisebb nyomatékú tengellyel

Mit jelent az Euler szám?
Mire használható?
Adja meg a mellékelt ábra Euler számát.

Az Euler-szám egyike a topológiai tulajdonságoknak, melyek egy kép geometriai leírását segítik elő. Fontos része az ilyen tulajdonságoknak, hogy rubber-sheet jellegű transzormációkra invariáns. Az ilyen jellegű tulajdonságok jól használhatók formák keresésére, objektumok felismerésére, adatbázisbeli keresésre. Euler-szám fontos szerepet játszik például orvosi képfeldolgozásban, fertőzött sejtek felismerésében.

Euler-szám = (egybefüggő régiók száma) – (lyukak száma)

Mit jelent a lánckód? Mire használható?
Mi a különbség a 4-szomszádos és 8-szomszédos lánckód között? Mik az előnyei és a hátrányai az így ábrázolt objektumoknak?
Hogyan tudunk segítségével kerület- és hossz-számítást végezni? Milyen problémák adódnak?

A lánckód egy veszteségmentes tömörítési algoritmus bináris képekhez. Lánckód segítségével alakfelismerést, sarokdetektálást végezhetünk. (A kódból egyértelműen látszik, hol vannak pl.: dudorok, bemélyedések.) Az objektum egy szélső pixelétől elindulva szomszédos, határ menti pixelekre lépkedünk. Attól függően, hogy milyen irányba lépünk tovább a pixelhez egy számot rendelünk hozzá. Ez a számsorozat alkotja a lánckódot.

• 4-szomszédos: csak azok a pixelek számítanak szomszédosnak, amiknek van közös élük
• 8-szomszédos: közös él, vagy közös csúcs

• 4-szomszédos lánckód maximális hiba: 41% (45°-os átlós egyenes)
• 8-szomszédos lánckód maximális hiba: 7.9% (~18-27°-os átlós egyenes)

Kerület = kódhossz

Hossz számításnál kerül elő az a probléma, hogy négyzetes pixelek esetén egy átlós lépés valóságos hossza sqrt(2) egység. 4-szomszédos lánckód 2 egység hosszúnak, míg a 8-szomszédos esetben 1 egység hosszúnak veszi alapból. Ha szükséges akkor ezt kompenzálni kell.

Számítógépes_látórendszerek_lánckód_1.jpg

Forrás

Ismertessen szubpixeles eljárásokat. Hogyan tudunk pozíciót, kerületet, ill. területet mérni segítségükkel?

Interpoláció alapú eljárás, mely segítségével pixel alatti pontossággal illeszthetünk görbét egy objektumra. Megfelelő algoritmussal akár 0.1% pontosság is elérhető.

Eljárás szürkeárnyalatos képekhez

1. Szürkeárnyalatos képeket először is binarizáljuk.
2. Visszatérve az eredeti képhez (fekete-fehér kép alapján) az átmeneteknél lévő pixelekhez egy súlytényezőt (értéke lehet tört, megadja az interpoláció finomságát) rendelünk attól függően, hogy mennyire világos/sötét az adott pixel.
3. Megfelelő ablakozással (pl.: 2x2) végigpásztázzuk a határokat és súlyozásoknak megfelelően felbontjuk (kijelöljük a határpontot/határpontokat) a két szomszédos fekete-fehér pixel középpontját összekötő szakaszt.

Pozíciószámítás során a 3. lépésben meghatározott határpontok koordinátáit használjuk fel a képletekben. Kerület, területnél hasonlóan.

Ismertesse az egyenesekre vonatkozó Hough-transzformáció működését.

Hough-transzformáció

A Hough-transzformáció segítségével a képen általában az Értelmezés sikertelen (formai hiba): {\displaystyle f (x, y ; a_1 , a_2 ,…, a_n)=0 } ahol Értelmezés sikertelen (formai hiba): {\displaystyle a_1, a_2,…, a_n } paraméterekkel explicit alakban megadható görbéket keressük. A Hough-transzformáció alkalmazása célravezető, ha ismert alakú (és méretű) objektumokat keresünk a képen. Akkor is célszerű, ha az egyenesek részben takartak vagy zajosak.

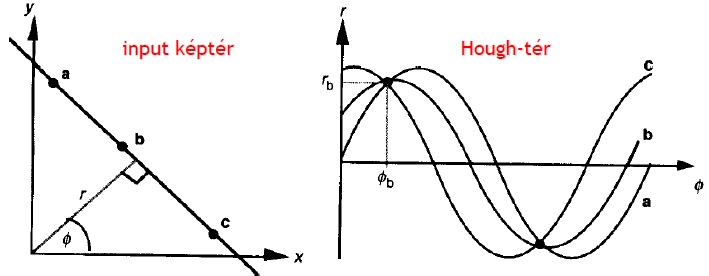
Áttérés a Hough-térbe

Az input (kép)tér egy $(x_{i},y_{i})$ pontjának az Értelmezés sikertelen (formai hiba): {\displaystyle r=x_i·\cosφ+y_i·\sinφ } szinuszos görbe felel meg a Hough-térben. Az egy egyenesbe eső pontokhoz tartozó szinuszos görbék egy pontban metszik egymást.

Egyenesek meghatározása

• Egy (él)pont a képtérben megfelel egy szinuszos görbének a Hough-térben.
• Két pontnak két görbe felel meg.
• Két (vagy több) ilyen görbe metszéspontja által reprezentált egyenesre ekkor kettő (vagy több) szavazat esett.
• Az így kapott egyenes valamennyi rá szavazó ponton átmegy a képtérben.
• A Hough-tér küszöbölésével megkapjuk a képtér egyeneseit.