„Laboratórium 2 - 8. Mérés ellenőrző kérdései” változatai közötti eltérés
Nincs szerkesztési összefoglaló |
|||
| 24. sor: | 24. sor: | ||
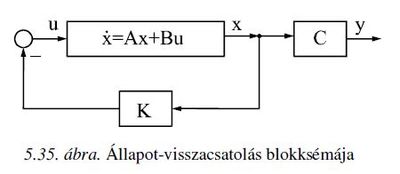
*A szakasz állapotegyenlete: <math>\dot{x}=Ax + Bu</math> | *A szakasz állapotegyenlete: <math>\dot{x}=Ax + Bu</math> | ||
*A zárt rendszer állapotegyenlete: <math>\dot{x}=(A-BK) \cdot x</math> | *A zárt rendszer állapotegyenlete: <math>\dot{x}=(A-BK) \cdot x</math> | ||
*A zárt rendszer karakterisztikus egyenlete: <math>\varphi_c(s)=det(sI-(A-BK))</math> | *A zárt rendszer karakterisztikus egyenlete: <math>\varphi_c(s)=det \; (sI-(A-BK))</math> | ||
Diszkrét időben: | Diszkrét időben: | ||
*A szakasz állapotegyenlete: <math>x_{i+1}=\Phi x_i + \Gamma u_i</math> | *A szakasz állapotegyenlete: <math>x_{i+1}=\Phi x_i + \Gamma u_i</math> | ||
*A zárt rendszer állapotegyenlete: <math>x_{i+1}=(\Phi-\Gamma K) \cdot x_i</math> | *A zárt rendszer állapotegyenlete: <math>x_{i+1}=(\Phi-\Gamma K) \cdot x_i</math> | ||
*A zárt rendszer állapotegyenlete: <math>\varphi_c(z)=(zI-(\Phi - \Gamma K))</math> | *A zárt rendszer állapotegyenlete: <math>\varphi_c(z)=det \; (zI-(\Phi - \Gamma K))</math> | ||
A pólusáthelyezési feladatban előírjuk a zárt rendszer karakterisztikus egyenletét (ami ekvivalens a zárt rendszer pólusainak, azaz a velük megegyező sajátértékeknek az előírásával), és keressük az ehhez szükséges állapot-visszacsatolást. Vegyük észre az algebrai hasonlóságot a folytonosidejű és diszkrétidejű feladat esetén. | A pólusáthelyezési feladatban előírjuk a zárt rendszer karakterisztikus egyenletét (ami ekvivalens a zárt rendszer pólusainak, azaz a velük megegyező sajátértékeknek az előírásával), és keressük az ehhez szükséges állapot-visszacsatolást. Vegyük észre az algebrai hasonlóságot a folytonosidejű és diszkrétidejű feladat esetén. | ||
A lap 2014. március 15., 19:40-kori változata
1. Milyen identifikációs rendszermodelleket ismer?
AR, ARX, IV, ARMAX stb. Ezek a modellek a MATLAB System Identification (röviden IDENT) toolboxa segítségével identifikálhatók. ARX modell a klasszikus LS (least squares) becsléssel is identifikálható. A módszerek érzékenyek a jel és zaj korreláltságára, amelyen segédváltozók (IV) alkalmazásával lehet javítani. Az ARMAX modell már általánosabb zajstruktúrát alkalmaz, de identifikációja numerikusan bonyolultabb módszert igényel, nevezetesen a kvázi Newton-módszert. Lásd elméleti alapok.
2. Miért van szükség identifikációra?
Az identifikáció célja dinamikus modell nyerése az ismeretlen rendszerről, a szabályozástechnikában a szabályozott szakaszról. Dinamikus modell hiányában csak kísérletezéssel tudnánk egyszerű szabályozók paraméterbeállítását megkeresni. A dinamikus modell ismerete lehetővé teszi elméletileg megalapozott szabályozások tervezését, amely minimálissá teszi a reális folyamaton való kísérletezést. A modell jó, ha azonos bemenő jel mellett a kimenetén hasonlóan válaszol, mint az ismeretlen rendszer. A modellel szemben pótlólagos elvárásaink is lehetnek, mint például az, hogy az identifikációval kapott diszkrétidejű modellnek legyen folytonosidejű megfelelője. Ez a negatív valós pólusokkal áll kapcsolatban a z-tartományban.
3. Mit értünk állapot-visszacsatolás alatt?
Állapot-visszacsatolás alatt azt értjük, hogy a szabályozó kimenő jelét (a beavatkozó jelet) az állapotokból állítjuk elő. Lineáris állapot-visszacsatolás esetén folytonos időben , diszkrét időben pedig , vagy röviden , ahol T a mintavételi idő. Egyváltozós (SISO) rendszer esetén K sorvektor.
4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete?
Folytonos időben:
- A szakasz állapotegyenlete:
- A zárt rendszer állapotegyenlete:
- A zárt rendszer karakterisztikus egyenlete:
Diszkrét időben:
- A szakasz állapotegyenlete:
- A zárt rendszer állapotegyenlete:
- A zárt rendszer állapotegyenlete:
A pólusáthelyezési feladatban előírjuk a zárt rendszer karakterisztikus egyenletét (ami ekvivalens a zárt rendszer pólusainak, azaz a velük megegyező sajátértékeknek az előírásával), és keressük az ehhez szükséges állapot-visszacsatolást. Vegyük észre az algebrai hasonlóságot a folytonosidejű és diszkrétidejű feladat esetén.
5. Mik a fő problémák az egyszerű u=-Kx állapot-visszacsatolás esetén tipikus irányítási rendszerekben?
Az egyik probléma az, hogy az állapotvektornak az összes komponense általában nem mérhető, például SISO esetben csak a kimenő jelet méri egy érzékelő, ezért állapotmegfigyelőt célszerű alkalmazni a becslés előállítására és bevonásába a beavatkozó jel számításába. A másik probléma, hogy az egyszerű állapot-visszacsatolás nem veszi figyelembe az alapjelet (más néven referencia jelet), ezért pótlólagos figyelembevételéről külön kell gondoskodni, lásd
6. Mi a domináns póluspár?
A szabályozási kör póluspárját dominánsnak nevezzük, ha a zárt szabályozási kör dinamikus minőségi jellemzőit lényegében határozza meg. Ennek feltétele, hogy a többi stabil pólusra teljesüljön , mert ekkor a többi pólus okozta tranziens már lecseng az első maximumig terjedő időpont , a túllövés és a beállási idő számításakor. Ebben az esetben jó közelítéssel:
7. Mi a kapcsolat a kéttárolós lengő tag csillapítása és csillapítatlan sajátfrekvenciája valamint a hozzátartozó pólusok között?
A kéttárolós lengő tag átviteli függvénye:
Pólusai:
Csillapítás:
Csillapítatlan sajátfrekvencia:
Aszimptotikus amplitúdó menete az helyen törésfrekvenciával rendelkezik, rezonanciahelye és az amplitúdó értéke a rezonancia helyén -től függ.
Nincs rezonancia, ha .
A átmeneti függvénynek ezzel szemben túllövése van, ha
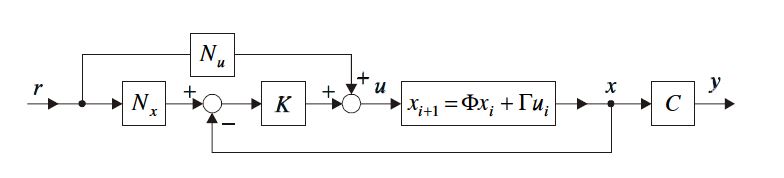
8. Mi biztosítja a konstans alapjel követését állapot-visszacsatolt rendszerekben?
Az alapjel követést az és az jelek biztosítják az állapot-visszacsatolt rendszerben, ahol és .
Diszkrét időben ezeket a következő feltételből lehet meghatározni:
9. Miért szükséges állapotmegfigyelő alkalmazása?
Az állapotvektornak általában nem mérhető az összes komponense, például SISO esetben csak az kimenő jelet méri egy érzékelő, ezért állapotmegfigyelőt célszerű alkalmazni a becslés előállítására és bevonásába a beavatkozó jel számításába folytonos időben , diszkrét időben pedig alakban. Az állapotmegfigyelő egy dinamikus rendszer, amelynek kimenete a becsült állapot, bemenete pedig a szakasz kimenete és a beavatkozó jel.
10. Mi a kapcsolat a "terhelés" elnevezés és a zavaró jel között?
Terhelés alatt a szabályozott szakasz bemenetére redukált zavaró jelet értjük.
11. Hogyan küszöbölhető ki a terhelés hatása?
Ha az állapotmegfigyelő becsülni tudja a bemenetre redukált zavarást is, akkor jó becslés esetén a szabályozó kimenetéhez hozzáadva a terhelés becslését, a zavarást kompenzálja a , és a rendszer úgy viselkedik, mintha nem is lenne zavarás.
12. Mit értünk diszkrétidejű aktuális megfigyelő alatt és mik az előnyei?
A diszkrétidejű aktuális állapotmegfigyelő állapotegyenlete:
Ha a becslési hiba, akkor választás esetén, ha a gerjesztetlen rendszer stabil és gyors, akkor rövid tranziens után a becslési hiba eltünik, és az állapot-visszacsatolásban helyettesíthető a vele már megegyező becsült állapottal.
Az aktuális megfigyelő előnye, hogy számításakor már figyelembe veszi az aktuális kimenő jelet, és ezáltal egy mintavételi időnyi holtidőt eliminál az irányítási algoritmusban, ami gyorsabb működést eredményezhet.
Mivel , ezért az aktuális állapotmegfigyelő tervezése algebrailag hasonló a pólusáthelyezési feladathoz, azaz előírt esetén a fiktív rendszerhez kell fiktív állapot-visszacsatolást tervezni.
13. Miért érdemes integrátort tenni a szabályozási körbe?
A szabályozási körbe integrátort helyezve javulnak az alapjel követési és zavaró jel elnyomási tulajdonságok, ha biztosítjuk a zárt rendszer stabilitását is. Az integrátor javítja a lassú paraméterváltozásokkal szembeni robusztusságot is mindaddig, amíg a paraméterváltozások ellenére a zárt rendszer stabil marad. Ennek oka, hogy az integrátor miatt a felnyitott kör erősítése alacsony frekvencián nagy (nulla frekvencián végtelen). Másrészt viszont alacsonyfrekvenciás pólus/zérus pár léphet fel a zárt rendszer átviteli függvényében, ami a dinamikus minőségi jellemzők romlásához vezethet.
14. Hogyan képződik le egy folytonos idejű pólus a diszkrétidejű tartományba?
A folytonosidejű pólus a helyre képződik le a pólusok számának és multiplicitásának megőrzése mellett.
Mivel , ezért páratlan multiplicitású negatív valós pólusú diszkrétidejű rendszernek nincs folytonosidejű megfelelője.
15. Mit okoznak a megfigyelő sajátértékei a zárt rendszer átviteli függvényében?
A megfigyelő sajátértékei a zárt rendszer átviteli függvényében pólus/zérus kiejtést okoznak.
A zárt rendszernek az egyszerűsítés után megmaradó pólusai a K állapot-visszacsatolás tervezésénél specifikált polinom gyökei lesznek, vagyis az állapotmegfigyelő alkalmazása nem módosítja a zárt rendszer megtervezett pólusait (feltéve, hogy a szabályozott szakasz modelljét pontosan ismerjük).