„Laboratórium 2 - 3. Mérés ellenőrző kérdései” változatai közötti eltérés
| 279. sor: | 279. sor: | ||
==12. Elektromágneses tereknél mit nevezünk közeltérnek illetve távoltérnek?== | ==12. Elektromágneses tereknél mit nevezünk közeltérnek illetve távoltérnek?== | ||
Közeltérnek nevezzük az antenna közelében létrehozott elektromágneses sugárzási teret, amelynek összetevői szabad térben az antennától mért távolság négyzetével, illetve köbével csökkennek. | |||
Távoltérnek nevezzük az antennától elég nagy - kb. 10 hullámhossznyinál nagyobb - távolságban létrehozott elektromágneses sugárzási teret, amelynek összetevői szabad térben az antennától mért távolsággal fordítottan ( 1/R ) arányosak. | |||
[[Category:Villanyalap]] | [[Category:Villanyalap]] | ||
A lap 2014. február 16., 03:07-kori változata
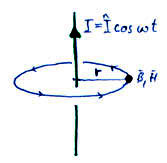
1. Határozza meg egy végtelen hosszú egyenes vezető mágneses terét!
Feladat: Egy végtelen hosszú, szinuszos áramot szállító vezetőtől távolságban lévő pontban határozza meg a térerősséget és a indukciót!
Megoldás:
Ábra:
Ampere-féle gerjesztési törvényt felírva egy olyan zárt L görbére, amely által kifeszített, a vezetékre merőleges A körlapot a vezeték pont a közepén döfi át:
Szimmetria okokból, a mágneses térerősségvektorok a görbe mentén mindenhol érintő irányúak, így a vonalintegrál egy egyszerű szorzássá egyszerűsödik. Az elektromos eltolásvektor időbeli változása zérus, az áramsűrűségvektor pedig merőleges az A körlapra, a felületintegrál eredménye az A körlapon átfolyó áramerősség:
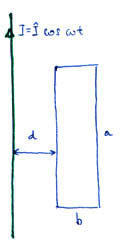
2. Határozza meg egy végtelen hosszú egyenes vezető környezetében elhelyezkedő vezetőkeretben indukált feszültséget!
Feladat: Egy végtelen hosszú, szinuszos áramot szállító vezető síkjában egy téglalap alakú, méretű vezetőkeret helyezkedik el. A vezetőkeret méretű oldala párhuzamos az áramot szállító vezetővel. Határozza meg a vezetőkeretben indukált feszültséget!
Megoldás
Ábra:
A Faraday-féle indukciós törvény felhasználásával:
Az integrálást tehát csak a oldal szerint végezzük el, mivel oldal mentén a mágneses térerősség állandó. A keret távolsága a vezetőtől .
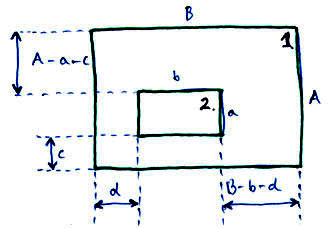
3. Határozza meg egy vezetőkeret rendszerben indukált feszültséget és kölcsönös induktivitást!
Feladat: Egy téglalap alakú, méretű, szinuszos áramot szállító vezetőkeret síkjában, a kereten belül egy második, méretű kisebb vezetőkeret aszimmetrikusan helyezkedik el. Az és illetve és méretű oldalak párhuzamosak. A legegyszerűbb modell alapján becsülve, közelítőleg mekkora feszültség indukálódik a második keretben? Mekkora a kölcsönös induktivitás?
Megoldás
Ábra:
Az alkalmazott modellben a külső keret által a belső keretben indukált feszültséget oly módon számítjuk, hogy a külső keret oldalait külön-külön, végtelen hosszú vezetőnek tekintjük, így felhasználható az előző kérdés megoldása:
A belső vezetőkeretben indukált feszültség a Faraday-féle indukciós térvénnyel egyszerűen számítható:
A kölcsönös induktivitás definíció szerint számítható:
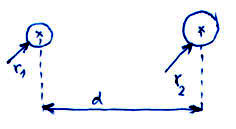
4. Határozza meg két végtelen hosszú, párhuzamosan futó hengeres vezető között a hosszegységre eső villamos kapacitást!
Ábra:
Vezessük be az alábbi jelöléseket:
- és
- Az sugarú vezetőhenger egységnyi hosszúságú szakaszára eső töltés
- Az sugarú vezetőhenger egységnyi hosszúságú szakaszára eső töltés
Egy töltött sugarú hengeres vezető által keltett elektromos térerősségvektor a Gauss-tétellel meghatározható, ha azt egy hosszúságú sugarú felületű koaxiális hengerre írjuk fel.
Szimmetria okok miatt az elektromos térerősségvektor mindig sugárirányú lesz, így a henger lapjain az integrál értéke zérus, míg hengerpaláston egy egyszerű szorzássá egyszerűsödik.
Az sugarú henger töltése potenciálkülönbséget hoz létre a két henger között.
Az sugarú henger töltése potenciálkülönbséget hoz létre a két henger között. Hasonló számítással adódik, hogy:
MIvel a potenciáltér lineáris, így a két henger közötti potenciálkülönbség:
A két hengeres vezető közötti hosszegységre eső kapacitás definíció szerint:
Ha mindkét henger azonos sugarú, azaz , abban az esetben:
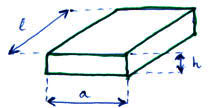
5. Határozza meg nyomtatott huzalozás esetén egy vezetőszakasz ellenállását és annak bizonytalanságát!
Ábra:
Ahol a fajlagos ellenállás, a vezetékszakasz hossza, a szélessége, pedig a vastagsága.
A hibakomponensek worst case összegzése esetén:
A hibakomponensek valószínűségi összegzésével, ami a tényleges bizonytalanságot adja:
6. Tanulmányozza a CD11.4599.151 típusú hálózati szűrő működését és műszaki adatait!
Műszaki adatok:
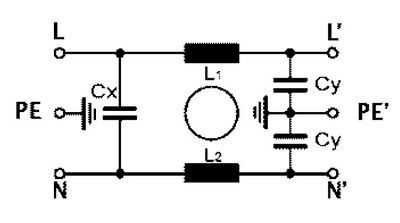
A CD11.4599.151 típusú szűrővel rendelkező hálózati csatlakozó 2 pólusú kapcsolója lengő vezetéken helyezkedik el. Névleges áramerőssége 1A, általános célú berendezésekbe tervezték, 1 pólusú beépített olvadóbiztosítékkal.
A belső elemek értékei: L= 2 x 10 mH, Cx = 68 nF, Cy = 2,2 nF.
A Cx és Cy kondenzátorok szigorú szabványok alapján tervezett, öngyógyuló dielektrikumos fóliakondenzátorok.
A szűrő kettős feladatot lát el:
- Az eszközre jutó feszültségcsúcsok ellen véd, amelyet elektromechanikus kapcsolók illetve relék okozhatnak.
- Ugyanez a szűrő a másik irányban is működik, az eszköz által keltett nagyfrekvenciás zavarokat csillapítja.
Működési elv:
A zavarokat feloszthatjuk közös és differenciális módusú zavarokra. Földeletlen zavarforrásból származó zavaró jel a tápáramhoz hasonló módon, az egyik vezetéken befolyik az eszközbe, a másikon pedig ki. Ezt nevezzük differenciális módusú zavaró jelnek. A közös módusú zavar ezzel szemben (a mechanikai kialakítás következtében) mindkét tápvezetéken folyik be az eszközbe, és a földelésen folyik vissza a zavarforráshoz.
A közös módusú zavarok csillapítása --> ld. 7. kérdés
A differenciális módusú zavarokat a fojtó csak kismértékben csillapítja (ld. 7. kérdés), ezért van szükség a Cy kondenzátorok beépítésére, amelyek viszont a védővezetőbe folyó (úgynevezett szivárgási) áramot okoznak. Ha a szivárgási áramra vonatkozó követelmény szigorú, ezeket el kell hagyni (pl. orvosi célú szűrők, melyekben a nagy Cx kapacitás kisütésére még egy ellenállást is beépítenek, hogy a táplálatlan szűrő kimenetén ne maradhasson fenn az üzemi feszültség).
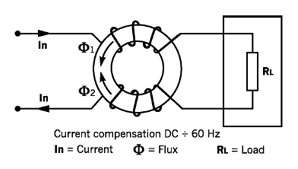
7. A szűrő közös vasmagon elhelyezett két tekercsének milyen a menetirányítása és miért?
A szűrő egy rádiófrekvenciás áramkompenzált fojtó (angolul RF Current Compensated Suppression Choke). A tekercsei úgy vannak irányítva, hogy a rajtuk folyó üzemi áramok által létrehozott fluxusok ellentétes irányúak legyenek, így kioltsák egymást. Ezek alapján, az áramirányok figyelembevételével mondhatjuk, hogy a tekercsek menetirányítása ellentétes.
Emiatt a differenciális módusú zavarok által keltett fluxusok (ideális esetben, azaz tökéletes csatolást feltéve) kioltják egymást. A közös módusú zavarok által keltett fluxusok viszont egyirányúak, így az ilyen zavarokat a fojtó szűrni tudja. A valóságban viszont a laza csatolás miatt fellépő szórási fluxus következtében a differenciális módusú zavarok kismértékű csillapítására is képes.
8. Adja meg a szűrő aszimmetrikus zavarjelre érvényes modelljét!
A hálózati szűrő kapcsolási rajza:
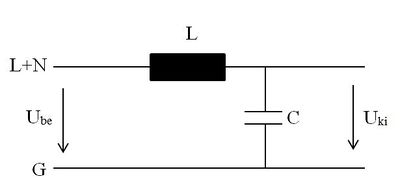
A szűrő aszimmetrikus zavarjelre érvényes modellje (Fázis + Nulla --> Védőföld)
9. Ideális elemeket feltételezve írja fel a szűrő csillapítását aszimmetrikus zavarjelre!
10. Adja meg a szűrő szimmetrikus zavarjelre érvényes modelljét!
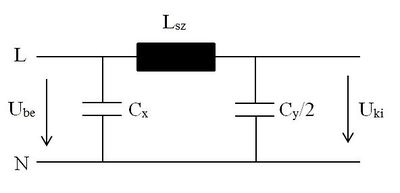
A hálózati szűrő kapcsolási rajza:
A szűrő szimmetrikus zavarjelre érvényes modellje (Fázis --> Nulla)
11. Ideális elemeket feltételezve írja fel a szűrő csillapítását szimmetrikus zavarjelre!
Ideális eset: (szivárgási induktivitás) A csillapítás egységnyi, a kimeneti feszültség bármely frekvencián megegyezik a bemeneti feszültséggel.
Valóságban:
A gyakorlatban adott frekvencián méréssel meghatározható, majd a képlettel számítható.
12. Elektromágneses tereknél mit nevezünk közeltérnek illetve távoltérnek?
Közeltérnek nevezzük az antenna közelében létrehozott elektromágneses sugárzási teret, amelynek összetevői szabad térben az antennától mért távolság négyzetével, illetve köbével csökkennek.
Távoltérnek nevezzük az antennától elég nagy - kb. 10 hullámhossznyinál nagyobb - távolságban létrehozott elektromágneses sugárzási teret, amelynek összetevői szabad térben az antennától mért távolsággal fordítottan ( 1/R ) arányosak.