Laboratórium 1 - 7. Mérés: Négypólusok vizsgálata

A mérésről

A beugró nagyrészt az ellenőrző kérdések közül kerül ki:

• 1:1 transzformátor mire jó?
• $\mu _{0}$ értéke
• Egy konkrét számításnál az erővonalhossz és a felület számítása (d és D adottak mint az 1.1 feladatban)
• Transzformátor helyettesítőképe (elektrotechnika jegyzetben ott van)
• Érdemes megtanulni a főbb mértékegységeket (pl: $B,H,\mu _{0}$ ...)

A mérések első 3 feladatát csináltuk meg, azok közül sem minden részletet (pl. 1.4, 1.5 kimaradt). A karakterisztika átszámításánál érdemes már otthon kiszámolni a skalártényezőt ami a két mennyiség között teremt kapcsolatot. Tehát valami $H=const\cdot I$, illetve $\mu _{0}=const_{2}\cdot Z$.

A két ajánlott irodalom alapos átolvasása nagyjából semmit sem segített :)

Házihoz segítség

Kidolgozott házi feladat

1.7 feladat: a kidolgozásban lévő válasz nem jó, a helyes megoldás: nem bírja a műszer lemérni a keresett értéket ekkora feszültségen és áramon.

1.9 feladat: Itt csak a Szekeres András-féle változat jó. "Infó a levlistáról: A tanár ma ezt mondta: A réz permeabilitása (műje) igazából Mű0. Mint a levegőjé, vagy bármely más nem mágnesezhető anyagé. Tehát a réz relatív permeabilitása 1, és permeabilitása mű0. Így kijön,hogy a behatolási mélység ~10mm(javítva), ami azt jelenti, hogy érdemes vastag rézvezetéket rakni a falba. Ha kicsi lenne a behatolási mélység (néhány mikron), akkor egy vékonyfalú cső is ugyanúgy megfelelne... és Dopeti kidolgozása: behatm = sqrt(2/(mu * szigma * omega) mu = mu0 omega = 2pi*f a rez fajlagos ellenállása 1.72x10-8 Ohm/m rez rel. permeabilitás = 1 behatm = sqrt(2/mu0) * sqrt(fajlagos ellenállás/(relatív permeabilitás * omega) = = sqrt(2/(mu0 * 2pi)) * sqrt(fajlell/(relperm * frek)) = = 503.29 * sqrt(fajlell / frek) = tovább gyúrva: =0.066 * sqrt(1/f) [méter] -> 66.006 * sqrt(1/f) [mm] tehát pl: 1Hz-en 6.6 cm a behatolási mélység, 50 Hz-en 9.33 mm 1 kHz-en 2mm 1 MHz-en 66 um "

Beugró kérdések kidolgozása

Nekünk volt beugró a következő kérdésekkel:

• B és H hogyan függ egymástól
• Hiszterézis görbe és a nevezetes pontjai
• Milyen veszteségek alakulnak ki egy tekercsben
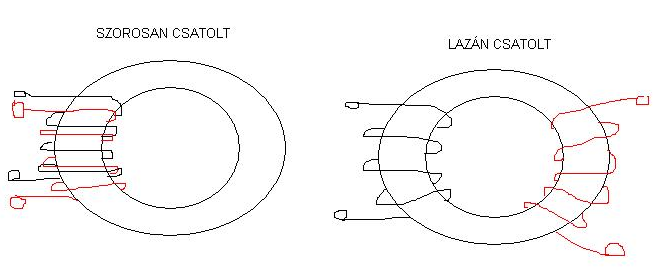
• Szorosan és lazán csatolt tekercs (ez sztem félreérthetően van a kidolgozásban uh küldtem fel róla)
• Z(f) jelleggörbe ideális és valós tekercsre ami azért sz*patós mert a 6.os laboron ezt mérted

Szorosan és Lazán csatolt tekercsek:

Szorosan csatolt tekercs: A szorosan csatolt tekercseket főleg a teljesítmény átvitelnél használják. Itt a főmező induktivitás nagyságrendekkel nagyobb mint a lazán csatolt tekercsnél (tehát ha pl mérésen csak 10% jön ki akkor vmit elszúrtatok) Kisebb a szórt impedancia is ami a kisebb szórt tér miatt van.

Lazán csatolt tekercs: Lazán csatolt tekercseket nagy feszültségen használják, mivel itt távolabb vannak a vezetékek, nehezebben üt át a vezeték.

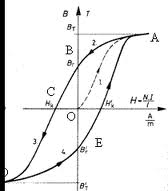
Hiszterézis görbe:

Br – Remanens indukció : ha megszünteted a mágneses teret ennyire marad mágneses a vas (ennyi lesz az indukció gerjesztés nélkül)

Hc -(az ábrán Hx) a Coercitiv erő : az a mágneses tér ami szükséges az anyag „Lemágnesezéséhez”

Bt - Telítési indukció: itt a vas telítésbe kerül a további mágneses tér növelésével. Gyakorlatilag nem nő az indukció tovább. (Tulajdonképpen nő, csak míg az első szakaszon a meredekség ~1000, a telítési szakaszon csak ~1).

Szűzgörbe: Az ábrán szaggatottal jelölt görbe az első felmágnesezéskor alakul ki. Első szakasza lineáris tartomány a második a permeabilitási tartomány a harmadik pedig a telítési tartomány

A hiszterézis görbe által körülzárt terület a hiszterézis veszteség.

Tekercs veszteségei:

• Vasveszteség:
  • Hiszterézis veszteség
  • Örvényáramú veszteség
• Rézveszteség

Impedanciamérés:

• 3 vezetékes, illetve 5 vezetékes impedancia mérés, működés,és kapcsolási rajz.