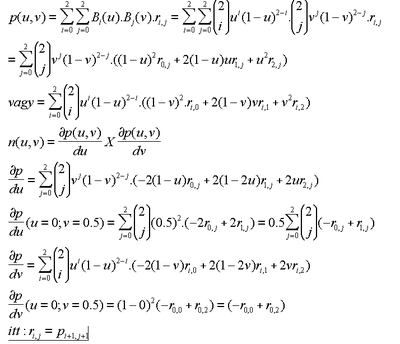„Grafika vizsga 20050104” változatai közötti eltérés
A VIK Wikiből
Új oldal, tartalma: „{{GlobalTemplate|Infoalap|SzgGrafVizsga20050104A}} [http://info.sch.bme.hu/document.php?cmd=download_proc&tmp_page=&doc_id=9719 infosite alapján] ==1.)== <b> Képek s…” |
Nincs szerkesztési összefoglaló |
||
| 1. sor: | 1. sor: | ||
__NOTOC__ | |||
==1.)== | ==1.)== | ||
; Képek szűrése a Fourier-térben. | |||
Képek szűrése a Fourier-térben. | : Alapelv: a képet Fourier-transzformáljuk, a frekvenciatartományban elvégzünk bizonyos műveleteket az együtthatókon, majd az eredményt visszatranszformáljuk. | ||
; Homályosítás | |||
: A Fourier-transzformáltban (FT) levágjuk a nagy frekvenciájú összetevőket, ezáltal elvesznek a részletek (élek, kontúrok). | |||
;"Laposítás" | |||
: Levágjuk a kis frekvenciájú összetevőket, a képből ezáltal elvesznek a lassú változások, de az élek megmaradnak (szürke foltos, lapos lesz a kép, de az alakokat ki lehet venni). | |||
; Élesítés | |||
: A FT-ban kiemeljük a nagy frekvenciájú összetevőket (5-20-as szorzó). Gond: a keletkezett képben a zaj is felerősödik. | |||
; Inverz szűrés (dekonvolúció): | |||
: A FT-at leosztjuk egy szóródási függvény FT-jával, ezzel látványos javulás érhető el (pl homályos kép kiélesítése). Problémák: | |||
A FT- | :: zaj | ||
:: kioltási vonalak | |||
:: ciklikusság | |||
:: wrap-around | |||
:: a súlyfüggvényt meg kell tudni állapítani, valódi kamerával felvett homályos képen az ún gradációs függvény inverzével is be kell szorozni | |||
==2.)== | ==2.)== | ||
;A hisztogram. Fényességi transzformációk | |||
A hisztogram. Fényességi transzformációk | |||
; Hisztogram: | |||
: Minden fényesség-értékre megadja az illető fényességgel rendelkező pontok számát a képen.<br> | |||
Minden fényesség-értékre megadja az illető fényességgel rendelkező pontok számát a képen.<br> | |||
Esetek: kevés árnyalaton kódolt kép, kiugró oszlop (túl- és alulexponált kép), kihasználatlan fényességi tartomány (sötét/világos részletek nem kivehetőek). | Esetek: kevés árnyalaton kódolt kép, kiugró oszlop (túl- és alulexponált kép), kihasználatlan fényességi tartomány (sötét/világos részletek nem kivehetőek). | ||
; Fényességi transzformáció: | |||
: Olyan (pixelenként végrehajtott) képfeldolgozó művelet, melynek eredménye kizárólag az aktuális képpont fényességétől függ. | |||
Olyan (pixelenként végrehajtott) képfeldolgozó művelet, melynek eredménye kizárólag az aktuális képpont fényességétől függ. | :: negálás | ||
:: fényesség-tartomány kinagyítása | |||
:: normálás | |||
:: vágás | |||
==3.)== | ==3.)== | ||
; Adott egy 9 vezérlőpontra illeszkedő 3x3-as Bezier felület. A vezérlőpontok rendre p11..p33. Adja meg a felület normálvektorát a (0 0.5) paraméterértékek mellett. | |||
Adott egy 9 vezérlőpontra illeszkedő 3x3-as Bezier felület. A vezérlőpontok rendre p11..p33. Adja meg a felület normálvektorát a (0 0.5) paraméterértékek mellett. | |||
A Bézier-felület egy szorzatfelület, így ha r(i,j) a vezérlopontok halmaza, akkor a felületet az alábbi explicit alakban lehet megadni ( 0 <= u, v <= 1): | : A Bézier-felület egy szorzatfelület, így ha r(i,j) a vezérlopontok halmaza, akkor a felületet az alábbi explicit alakban lehet megadni ( 0 <= u, v <= 1): | ||
: [[File:grafika_vizsga_20050104_3feladat.PNG|400px]] | |||
==4.)== | ==4.)== | ||
; Hogyan váltoik az előző feldataban kiszámolt normálvektor, ha a vezérlőpontokat a T homogén lineáris transzormációs mátrixszal megoszorozzuk. | |||
Hogyan | |||
: <math> T = \left[ \begin{array}{rrrr} 2 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 4 & 0 \\ 6 & 7 & 8 & 1 \\ \end{array} \right] </math> | |||
:A feladat a látszat ellenére teljesen független a harmadik feladattól. Az eltolás (azaz a 4x4-es transzformáló mátrix alsó sora) a normálvektort nem változtatja meg, ezért elég a bal felsõ 3x3-as részmátrixot tekinteni, ami tengelyek menti skálázást hajt végre. | |||
:A megoldási mód, ahogyan az az előadásokon is elhangzott, a mátrix inverzének a transzponáltjával való szorzás jobbról. A mátrix inverze a főátlóbeli elemek reciprokukra cserélésével kapható, a transzponált pedig nem változtat semmit a mátrixon, hisz az szimmetrikus. Tehát az új n'=(x1,y1,t1) normálvektor koordinátái x1=x0/2, y1=y0/3, z1=z0/4, ha az eredeti normálvektor n=(x0,y0,z0), és a skálázó mátrix fõátlója (2,3,4), és a mátrix diagonális. | |||
==5.)== | ==5.)== | ||
; Írja fel a 3D projektív tér összes ideális síkjának és ideális egyenesének egyenletét (az ideális térelem csak ideális pontokat tartalmaz. Hány ideális sík és egyenes van? | |||
Írja fel a 3D projektív tér összes ideális síkjának és ideális egyenesének egyenletét (az ideális térelem csak ideális pontokat tartalmaz. Hány ideális sík és egyenes van? | |||
==6.)== | ==6.)== | ||
; Az alábbi lövedék röpül a hegyes végét elől tartva( úgy, ahogy egy tisztessséges lövedéktől elvárható) a 3D virtuális térben (lásd lent). A lövedék hengeres részének magassága 4m, a kúpos részének magassága 2m, átmérője 1.5m. A lövedék végének középpontja [x0 y0 z0] pontról indul [vx0 vy0 vz0] kezdősebességgel. A lövedék az űgyúscső hornyolása miatt f [fok/sec] szögsebességgel forog a főtengelye körül. A nehézségi gyorsulás g [m/sec^2] a közöegellenállás elhanyagolható, ütközés nincs. Írjon C föggvényt, amely képletanimációval meghatározza a t pillanatban érvényes mozgásaállapotot, és OpenGL függvényhívások segítségével fel is rajzolja a lövedéket. A rajzoláshoz felhasználhatja a Henger függvényt, amley egy 1mmagasságú origó középpontú z tengelyű 1m átmérőjű hengert jelenít meg, és a kúp vüggvényt mely egy xy álló, 1m magas 1m átmérős alapkörrel rendelkező kúpot rajzol fel. | |||
Az alábbi lövedék röpül a hegyes végét elől tartva( úgy, ahogy egy tisztessséges lövedéktől elvárható) a 3D virtuális térben (lásd lent). A lövedék hengeres részének magassága 4m, a kúpos részének magassága 2m, átmérője 1.5m. A lövedék végének középpontja [x0 y0 z0] pontról indul [vx0 vy0 vz0] kezdősebességgel. A lövedék az űgyúscső hornyolása miatt f [fok/sec] szögsebességgel forog a főtengelye körül. A nehézségi gyorsulás g [m/sec^2] a közöegellenállás elhanyagolható, ütközés nincs. Írjon C föggvényt, amely képletanimációval meghatározza a t pillanatban érvényes mozgásaállapotot, és OpenGL függvényhívások segítségével fel is rajzolja a lövedéket. A rajzoláshoz felhasználhatja a Henger függvényt, amley egy 1mmagasságú origó középpontú z tengelyű 1m átmérőjű hengert jelenít meg, és a kúp vüggvényt mely egy xy álló, 1m magas 1m átmérős alapkörrel rendelkező kúpot rajzol fel | |||
[[Category:Infoalap]] | [[Category:Infoalap]] | ||
A lap 2013. október 15., 09:21-kori változata
1.)
- Képek szűrése a Fourier-térben.
- Alapelv: a képet Fourier-transzformáljuk, a frekvenciatartományban elvégzünk bizonyos műveleteket az együtthatókon, majd az eredményt visszatranszformáljuk.
- Homályosítás
- A Fourier-transzformáltban (FT) levágjuk a nagy frekvenciájú összetevőket, ezáltal elvesznek a részletek (élek, kontúrok).
- "Laposítás"
- Levágjuk a kis frekvenciájú összetevőket, a képből ezáltal elvesznek a lassú változások, de az élek megmaradnak (szürke foltos, lapos lesz a kép, de az alakokat ki lehet venni).
- Élesítés
- A FT-ban kiemeljük a nagy frekvenciájú összetevőket (5-20-as szorzó). Gond: a keletkezett képben a zaj is felerősödik.
- Inverz szűrés (dekonvolúció)
- A FT-at leosztjuk egy szóródási függvény FT-jával, ezzel látványos javulás érhető el (pl homályos kép kiélesítése). Problémák:
- zaj
- kioltási vonalak
- ciklikusság
- wrap-around
- a súlyfüggvényt meg kell tudni állapítani, valódi kamerával felvett homályos képen az ún gradációs függvény inverzével is be kell szorozni
2.)
- A hisztogram. Fényességi transzformációk
- Hisztogram
- Minden fényesség-értékre megadja az illető fényességgel rendelkező pontok számát a képen.
Esetek: kevés árnyalaton kódolt kép, kiugró oszlop (túl- és alulexponált kép), kihasználatlan fényességi tartomány (sötét/világos részletek nem kivehetőek).
- Fényességi transzformáció
- Olyan (pixelenként végrehajtott) képfeldolgozó művelet, melynek eredménye kizárólag az aktuális képpont fényességétől függ.
- negálás
- fényesség-tartomány kinagyítása
- normálás
- vágás
3.)
- Adott egy 9 vezérlőpontra illeszkedő 3x3-as Bezier felület. A vezérlőpontok rendre p11..p33. Adja meg a felület normálvektorát a (0 0.5) paraméterértékek mellett.
- A Bézier-felület egy szorzatfelület, így ha r(i,j) a vezérlopontok halmaza, akkor a felületet az alábbi explicit alakban lehet megadni ( 0 <= u, v <= 1):
4.)
- Hogyan váltoik az előző feldataban kiszámolt normálvektor, ha a vezérlőpontokat a T homogén lineáris transzormációs mátrixszal megoszorozzuk.
- A feladat a látszat ellenére teljesen független a harmadik feladattól. Az eltolás (azaz a 4x4-es transzformáló mátrix alsó sora) a normálvektort nem változtatja meg, ezért elég a bal felsõ 3x3-as részmátrixot tekinteni, ami tengelyek menti skálázást hajt végre.
- A megoldási mód, ahogyan az az előadásokon is elhangzott, a mátrix inverzének a transzponáltjával való szorzás jobbról. A mátrix inverze a főátlóbeli elemek reciprokukra cserélésével kapható, a transzponált pedig nem változtat semmit a mátrixon, hisz az szimmetrikus. Tehát az új n'=(x1,y1,t1) normálvektor koordinátái x1=x0/2, y1=y0/3, z1=z0/4, ha az eredeti normálvektor n=(x0,y0,z0), és a skálázó mátrix fõátlója (2,3,4), és a mátrix diagonális.
5.)
- Írja fel a 3D projektív tér összes ideális síkjának és ideális egyenesének egyenletét (az ideális térelem csak ideális pontokat tartalmaz. Hány ideális sík és egyenes van?
6.)
- Az alábbi lövedék röpül a hegyes végét elől tartva( úgy, ahogy egy tisztessséges lövedéktől elvárható) a 3D virtuális térben (lásd lent). A lövedék hengeres részének magassága 4m, a kúpos részének magassága 2m, átmérője 1.5m. A lövedék végének középpontja [x0 y0 z0] pontról indul [vx0 vy0 vz0] kezdősebességgel. A lövedék az űgyúscső hornyolása miatt f [fok/sec] szögsebességgel forog a főtengelye körül. A nehézségi gyorsulás g [m/sec^2] a közöegellenállás elhanyagolható, ütközés nincs. Írjon C föggvényt, amely képletanimációval meghatározza a t pillanatban érvényes mozgásaállapotot, és OpenGL függvényhívások segítségével fel is rajzolja a lövedéket. A rajzoláshoz felhasználhatja a Henger függvényt, amley egy 1mmagasságú origó középpontú z tengelyű 1m átmérőjű hengert jelenít meg, és a kúp vüggvényt mely egy xy álló, 1m magas 1m átmérős alapkörrel rendelkező kúpot rajzol fel.