„Algoritmuselmélet - PPZH, 2013.05.23.” változatai közötti eltérés
A VIK Wikiből
| 62. sor: | 62. sor: | ||
}} | }} | ||
===5. Feladat=== | ===5. Feladat (Van megoldás)=== | ||
Egy kupac elemeit preorder bejárás szerint kiolvasva az alábbi számsorozatot kapjuk: <math> 1, 17, 19, 21, 22, 31, 37, 2, 8, 3.</math> Rekonstruálható-e ebből a kupac? | Egy kupac elemeit preorder bejárás szerint kiolvasva az alábbi számsorozatot kapjuk: <math> 1, 17, 19, 21, 22, 31, 37, 2, 8, 3.</math> Rekonstruálható-e ebből a kupac? | ||
{{Rejtett | {{Rejtett | ||
A lap 2013. június 18., 21:07-kori változata
2013.05.23 - PPZH megoldásai
1. Feladat (Van megoldás)
Tudjuk, hogy az Értelmezés sikertelen (ismeretlen „\textsc” függvény): {\displaystyle f(n), g(n) : \textsc{N} \rightarrow \textsc{N} } függvényekre igaz, hogy és Lehetséges-e, hogy:
(a)
(b)
(Ez két, egymástól függetlenül megválaszolandó kérdés.)
Megoldás
a)
- Ha
- Akkor igaz az, hogy:
- És az is, hogy
- Tehát lehetséges.
b)
- Ha
- Akkor igaz az, hogy:
- És az is, hogy
- Tehát lehetséges.
2. Feladat
TODO
Megoldás
TODO
3. Feladat
TODO
Megoldás
TODO
4. Feladat
TODO
Megoldás
TODO
5. Feladat (Van megoldás)
Egy kupac elemeit preorder bejárás szerint kiolvasva az alábbi számsorozatot kapjuk: Rekonstruálható-e ebből a kupac?
Megoldás
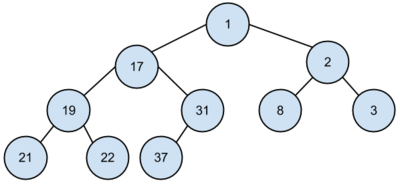
- A kupac egy teljes bináris fa, így tudjuk, hogy mi a fa alakja.
- Nincs is más dolgunk, mint felrajzolni, majd a preorder bejárás alapján beírni az elemeket a megfelelő csúcsokba, és ellenőrizni, hogy sérül-e valahol a kupac adatszerkezet egy tulajdonsága.
- Látszik, hogy minden rendben van, így a kupac rekonstruálható.
6. Feladat
TODO
Megoldás
TODO
7. Feladat
TODO
Megoldás
TODO
8. Feladat
TODO
Megoldás
TODO