„Laboratórium 1 - 2005 őszi ZH megoldások” változatai közötti eltérés
a David14 átnevezte a(z) Labor 1. 2005 ZH lapot a következő névre: Laboratórium 1 - 2005 őszi ZH megoldások |
aNincs szerkesztési összefoglaló |
||
| 1. sor: | 1. sor: | ||
== 1. Feladat == | |||
'''Határozza meg egy egyenfeszültségű generátor Thevenin helyettesítőképének elemeit (U0,Rb) a következő mérési eredmények alapján: U1=10V, U2=9.88V. Az U1 kapocsfeszültséget terhelés nélkül, az U2-t Rt=1kOhm terheléssel mértük.''' | |||
==== | * Terheletlen esetben: <math> U_0 = U_1 </math> | ||
* Terhelt esetben: <math> U_{rb} = U_0 - U_2 </math> (<math> R_b </math> -n eső fesz), <math> \frac{U_{rb}}{U_2} = \frac{R_b}{R_t} \Rightarrow R_b = \frac{(U0-U2)Rt}{U_2} = 0.012k \Omega</math> | |||
== 2. Feladat == | |||
'''Két azonos frekvenciájú szinuszjel közötti fázistolást szeretnénk megmérni Lissajous-módszerrel.''' | |||
'''a) Rajzolja fel az oszcilloszkópon látható ábrát!''' | |||
<math> \varphi = \frac{\Delta t}{T}*360^{\circ} </math> | |||
<math> \varphi = \arcsin(\frac{c}{d}) </math> | * Méréskönyv 169.oldal, vagy labor segédlet 34.oldal. | ||
<math> c = 2*Y_p*\sin \varphi, d = 2*Y_p </math>, | [[Fájl:Labor1 kép1.bmp]] | ||
'''b) Adja meg a fázistolás származtatási összefüggését és a változók jelentését!''' | |||
*<math> \varphi = \frac{\Delta t}{T}*360^{\circ} </math> | |||
*<math> \varphi = \arcsin(\frac{c}{d}) </math> | |||
*<math> c = 2*Y_p*\sin \varphi, d = 2*Y_p </math>, | |||
*Ahol c a tengelymetszetek távolsága, d pedig a legnagyobb távolság. | |||
'''c) Milyen üzemmódban használjuk az oszcilloszkópot (időalap)?''' | |||
* XY üzemmód | * XY üzemmód | ||
'''d) Hogyan befolyásolja az időalap generátor nemlinearitása a mérést?''' | |||
* | |||
* Nem függ tőle a pontosság, mivel az eltérítést külső jelek végzik. | |||
* Nem befolyásolja a generátor erősítési hibája sem, mivel hányadosképzés miatt a hiba kiesik. | * Nem befolyásolja a generátor erősítési hibája sem, mivel hányadosképzés miatt a hiba kiesik. | ||
* Kalibrált állás fontos, mert ekkor van a földpont a képernyő közepén. | * Kalibrált állás fontos, mert ekkor van a földpont a képernyő közepén. | ||
==== | == 3. Feladat == | ||
'''Az oszcilloszkóp FFT funkciójával 3 csúcsot látunk, melyek frekvenciája 100, 300 és 500 Hz, amplitudója rendre -5.35, -14.89, -19.33dB. Ideális négyszögjel, vagy háromszögjel a bemenet? Hány Hz a bemenőjel alapfrekvenciája? (megjegyzés: a szkópon 0dBV nagyságú csúcs jelenik meg 1V effektív értékű szinuszjel esetén, úgy tekintjük, hogy az FFT a spektrumot torzítatlanul méri)''' | |||
* Ideális négyszögjel: <math> \frac{1}{x} </math> szerint változik | * Ideális négyszögjel: <math> \frac{1}{x} </math> szerint változik | ||
| 32. sor: | 40. sor: | ||
Az alapfrekvencia pedig 100 Hz. | Az alapfrekvencia pedig 100 Hz. | ||
Megjegyzés: | Kiszámolhatóak a dBV értékekből a feszültség értékek <math> U = 10^{\frac{U_{dBV}}{20}} </math>, majd a feszültségek arányai: U2/U1 = 1/3 illetve U3/U1 = 1/5. Ebből látszik, hogy a megadott jel négyszögjel, mert spektruma 1/x szerű a páratlan felharmonikusoknál. Háromszögjelnél 1/9 illetve 1/25 lenne a két arány. | ||
Megjegyzés: Nyilvánvalóan fölösleges munka kiszámolni a feszültségeket, a dBV értékekből is hasonló következtetést lehet levonni. | |||
== 4. Feladat == | |||
'''Rajzolja fel egy valódi kondenzátor négyelemű modelljét. Milyen fizikai hatásokat reprezentálnak az egyes elemek? Adja meg a modell reaktáns elemeinek segítségével a rezonanciafrekvenciát!''' | |||
[[Fájl:Labor1 kép2.JPG]] | |||
Rezonancia frekvencia: <math> f = \frac{1}{2 \pi \sqrt{LC}} </math> | |||
<math> \omega = \frac{1}{\sqrt{LC}} </math> | |||
<math> Z = R + j \omega L + \frac{1}{j\omega C} </math> | |||
== 5. Feladat == | |||
'''Egy telecom trafót egy R0=600 Ohm-os feszültségforrás és egy Rt=600 Ohm-os terhelés illesztett elválasztására használunk. Az adatok: N2=1000, R2=10 Ohm, N1=a*N2, R1=a*R2, ahol N2 és N1 rendre a szekunder és a primer menetszám, R2 és R1 pedig rendre a szekunder és a primer rézellenállás. Rajzolja fel a kapcsolást, benne a trafó modelljével. A szórási induktivitás és a mágnesezőáram elhanyagolható. Mekkora a szükséges primer menetszám?''' | |||
Általános megoldás: | |||
* | Rb = R1 + n^2*R2 + n^2*Rt ,ahol: | ||
*Rb - generátor belső ellenállása | |||
*R1,R2 - tekercsek DC ellenállása | |||
*Rt - terhelő ellenállás | |||
*n - menetszám áttétel n = N_primer / N_szekunder | |||
Magyarázat: A fő cél a reflexiómentesség, ezt úgy érhetjük el, hogy illesztett lezárást alkalmazunk. Azaz a generátor belső ellenállásának és a terhelésnek meg kell egyeznie. A terhelés esetünkben összetett: tekercsek DC ellenállása, és a terhelő ellenállás. És ezek nem egyszerűen kapcsolódnak a trafó miatt. Ha a primer oldalról benézünk, akkor a szekunder DC ellenállás és a terhelő ellenállás n^2-szeresét látjuk. Ezért ez a képlet. | |||
== | == 6. Feladat == | ||
'''Rajzolja fel egy bipoláris tranzisztor közös (földelt) emmitteres kimeneti (Ic-Uce) karakterisztikáját! Jelöljön be az aktív tartományban egy munkapontot és írja le hogyan mérné meg a tranzisztor h11, h21, h22 (hibrid) paramétereit!''' | |||
A megoldások megtalálhatóak az Elektronika I. könyvben. A kimeneti karakterisztika az 5-30as oldalon, a hibrid paraméterek számítási módjai pedig az 5-51 - 5-53as oldalakon. Illetve itt is be van mutatva egy példán (és talán inkább ezt kérnék ennél a példánál): | |||
[[Fájl:Labor1 kép3.JPG]] | |||
== 7. Feladat == | |||
'''Egy D flip-flopot a következő gyári adatok jellemeznek: <math>t_{su}</math>= 20 ns set-up time, <math>t_h</math>= 8 ns hold time''' | |||
'''a) A D flip-flopot egy áramkörbe építve annak órajele a helytelen kapcsolási elrendezés és vezetékezés miatt az adatjelhez képest 5ns-mal késik. Mekkora a módosult flip-flopnak a tsn és th értéke?''' | |||
<math>t_{setup} = 20 - 5 =15</math> nsec | |||
<math>t_{hold}= 8 + 5 = 13</math> nsec | |||
'''b) Hogyan módosulnak ezek az adatok, ha az 5ns-os késleltetés az adatvonalon lenne?''' | |||
<math>t_{setup} = 20 + 5 =25</math> nsec | |||
<math>t_{hold}= 8 - 5 = 3</math> nsec | |||
== | == 8. Feladat == | ||
'''Egy decimális számlálóval frekvenciaosztót képeztünk, amellyel egy kb 50MHz frekvenciájú, szimmetrikus kitöltésű négyszögjelet osztunk le ( A leosztandó négyszögjel a számláló órajelét képezi).''' | |||
'''a) Megmérjük a leosztott jel egy periódusát a LogicWave logikai analizátorral időzítésanalízis üzemmódban, a lehető legnagyobb pontossággal. Becsülje meg a mérés relatív hibáját!''' | |||
'''b) Hogyan módosul az előbbi hibaalap, ha a kurzorok segítségével nem egy, hanem 5 periódus idejét mérjük le?''' | |||
'''c) Megmérhető-e a leosztott jel periódusideje a LogicWave logikai analizátor állapotanalízis üzemmódjával? + meg vannak adva adatok...''' | |||
== 9. Feladat == | |||
'''Rajzolja fel a 4 számjegyű 7 szegmenses kijelző egység jellemző hullámformáit időmultiplex számjegykiválasztás esetére! Milyen időzítéseket érdemes használni a "jól látható" kijelzés érdekében?''' | |||
Az időmultiplexált kijelzőnél az összes kijelző ugyanazt a 7 szegmenses kódolású adatot kapja. Azonban egyszerre mindig csak egy kijelző van engedélyezve (a dekóderrel), az amelyhez tartozik az adat. Ezután a következő adat kerül a buszra (a multiplexer által), s a következő kijelző lesz engedélyezve. Ez ismétlődik ciklikusan olyan sebességgel, hogy az emberi szem egyszerre látja az összes karakter. Ehhez egy karakterre 25 Hz-nél sűrűbben kel hogy sor kerüljön. Így a számlálót n kijelző esetén legalább n*25 Hz-el kell léptetni. | |||
== 10. Feladat == | |||
'''Adjon egy olyan tesztvektor sorozatot, az alábbi egyetlen X bemenettel rendelkező automatához amely leteszteli az automata összes állapotátmenetét!''' | |||
[[Fájl:Labor1 kép4.GIF]] | |||
{| border="1" | {| border="1" | ||
| 86. sor: | 124. sor: | ||
| allapot || A || B || B || C || C || B || A || C | | allapot || A || B || B || C || C || B || A || C | ||
|} | |} | ||
[[Category:Villanyalap]] | [[Category:Villanyalap]] | ||
A lap 2013. február 7., 20:41-kori változata
1. Feladat
Határozza meg egy egyenfeszültségű generátor Thevenin helyettesítőképének elemeit (U0,Rb) a következő mérési eredmények alapján: U1=10V, U2=9.88V. Az U1 kapocsfeszültséget terhelés nélkül, az U2-t Rt=1kOhm terheléssel mértük.
- Terheletlen esetben:
- Terhelt esetben: ( -n eső fesz),
2. Feladat
Két azonos frekvenciájú szinuszjel közötti fázistolást szeretnénk megmérni Lissajous-módszerrel.
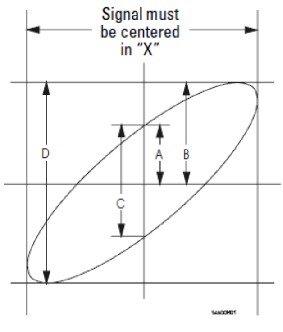
a) Rajzolja fel az oszcilloszkópon látható ábrát!
- Méréskönyv 169.oldal, vagy labor segédlet 34.oldal.
b) Adja meg a fázistolás származtatási összefüggését és a változók jelentését!
- ,
- Ahol c a tengelymetszetek távolsága, d pedig a legnagyobb távolság.
c) Milyen üzemmódban használjuk az oszcilloszkópot (időalap)?
- XY üzemmód
d) Hogyan befolyásolja az időalap generátor nemlinearitása a mérést?
- Nem függ tőle a pontosság, mivel az eltérítést külső jelek végzik.
- Nem befolyásolja a generátor erősítési hibája sem, mivel hányadosképzés miatt a hiba kiesik.
- Kalibrált állás fontos, mert ekkor van a földpont a képernyő közepén.
3. Feladat
Az oszcilloszkóp FFT funkciójával 3 csúcsot látunk, melyek frekvenciája 100, 300 és 500 Hz, amplitudója rendre -5.35, -14.89, -19.33dB. Ideális négyszögjel, vagy háromszögjel a bemenet? Hány Hz a bemenőjel alapfrekvenciája? (megjegyzés: a szkópon 0dBV nagyságú csúcs jelenik meg 1V effektív értékű szinuszjel esetén, úgy tekintjük, hogy az FFT a spektrumot torzítatlanul méri)
- Ideális négyszögjel: szerint változik
- Ideális háromszögjel: szerint változik
Az alapfrekvencia pedig 100 Hz.
Kiszámolhatóak a dBV értékekből a feszültség értékek , majd a feszültségek arányai: U2/U1 = 1/3 illetve U3/U1 = 1/5. Ebből látszik, hogy a megadott jel négyszögjel, mert spektruma 1/x szerű a páratlan felharmonikusoknál. Háromszögjelnél 1/9 illetve 1/25 lenne a két arány.
Megjegyzés: Nyilvánvalóan fölösleges munka kiszámolni a feszültségeket, a dBV értékekből is hasonló következtetést lehet levonni.
4. Feladat
Rajzolja fel egy valódi kondenzátor négyelemű modelljét. Milyen fizikai hatásokat reprezentálnak az egyes elemek? Adja meg a modell reaktáns elemeinek segítségével a rezonanciafrekvenciát!
Rezonancia frekvencia:
5. Feladat
Egy telecom trafót egy R0=600 Ohm-os feszültségforrás és egy Rt=600 Ohm-os terhelés illesztett elválasztására használunk. Az adatok: N2=1000, R2=10 Ohm, N1=a*N2, R1=a*R2, ahol N2 és N1 rendre a szekunder és a primer menetszám, R2 és R1 pedig rendre a szekunder és a primer rézellenállás. Rajzolja fel a kapcsolást, benne a trafó modelljével. A szórási induktivitás és a mágnesezőáram elhanyagolható. Mekkora a szükséges primer menetszám?
Általános megoldás:
Rb = R1 + n^2*R2 + n^2*Rt ,ahol:
- Rb - generátor belső ellenállása
- R1,R2 - tekercsek DC ellenállása
- Rt - terhelő ellenállás
- n - menetszám áttétel n = N_primer / N_szekunder
Magyarázat: A fő cél a reflexiómentesség, ezt úgy érhetjük el, hogy illesztett lezárást alkalmazunk. Azaz a generátor belső ellenállásának és a terhelésnek meg kell egyeznie. A terhelés esetünkben összetett: tekercsek DC ellenállása, és a terhelő ellenállás. És ezek nem egyszerűen kapcsolódnak a trafó miatt. Ha a primer oldalról benézünk, akkor a szekunder DC ellenállás és a terhelő ellenállás n^2-szeresét látjuk. Ezért ez a képlet.
6. Feladat
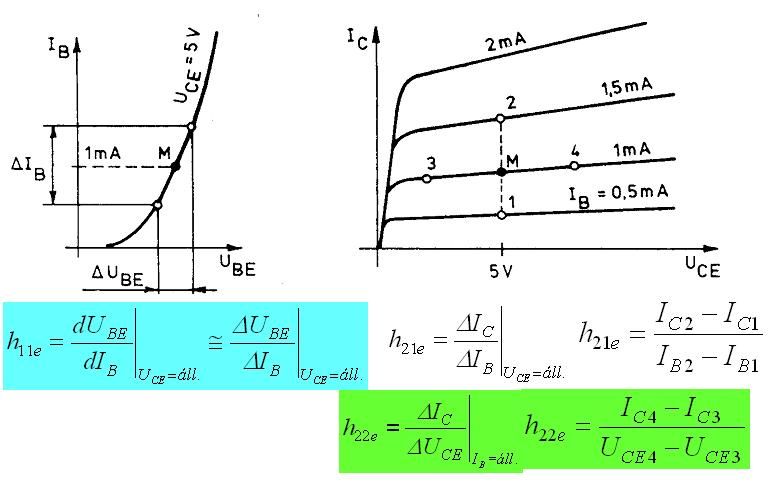
Rajzolja fel egy bipoláris tranzisztor közös (földelt) emmitteres kimeneti (Ic-Uce) karakterisztikáját! Jelöljön be az aktív tartományban egy munkapontot és írja le hogyan mérné meg a tranzisztor h11, h21, h22 (hibrid) paramétereit!
A megoldások megtalálhatóak az Elektronika I. könyvben. A kimeneti karakterisztika az 5-30as oldalon, a hibrid paraméterek számítási módjai pedig az 5-51 - 5-53as oldalakon. Illetve itt is be van mutatva egy példán (és talán inkább ezt kérnék ennél a példánál):
7. Feladat
Egy D flip-flopot a következő gyári adatok jellemeznek: = 20 ns set-up time, = 8 ns hold time
a) A D flip-flopot egy áramkörbe építve annak órajele a helytelen kapcsolási elrendezés és vezetékezés miatt az adatjelhez képest 5ns-mal késik. Mekkora a módosult flip-flopnak a tsn és th értéke?
nsec
nsec
b) Hogyan módosulnak ezek az adatok, ha az 5ns-os késleltetés az adatvonalon lenne?
nsec
nsec
8. Feladat
Egy decimális számlálóval frekvenciaosztót képeztünk, amellyel egy kb 50MHz frekvenciájú, szimmetrikus kitöltésű négyszögjelet osztunk le ( A leosztandó négyszögjel a számláló órajelét képezi).
a) Megmérjük a leosztott jel egy periódusát a LogicWave logikai analizátorral időzítésanalízis üzemmódban, a lehető legnagyobb pontossággal. Becsülje meg a mérés relatív hibáját!
b) Hogyan módosul az előbbi hibaalap, ha a kurzorok segítségével nem egy, hanem 5 periódus idejét mérjük le?
c) Megmérhető-e a leosztott jel periódusideje a LogicWave logikai analizátor állapotanalízis üzemmódjával? + meg vannak adva adatok...
9. Feladat
Rajzolja fel a 4 számjegyű 7 szegmenses kijelző egység jellemző hullámformáit időmultiplex számjegykiválasztás esetére! Milyen időzítéseket érdemes használni a "jól látható" kijelzés érdekében?
Az időmultiplexált kijelzőnél az összes kijelző ugyanazt a 7 szegmenses kódolású adatot kapja. Azonban egyszerre mindig csak egy kijelző van engedélyezve (a dekóderrel), az amelyhez tartozik az adat. Ezután a következő adat kerül a buszra (a multiplexer által), s a következő kijelző lesz engedélyezve. Ez ismétlődik ciklikusan olyan sebességgel, hogy az emberi szem egyszerre látja az összes karakter. Ehhez egy karakterre 25 Hz-nél sűrűbben kel hogy sor kerüljön. Így a számlálót n kijelző esetén legalább n*25 Hz-el kell léptetni.
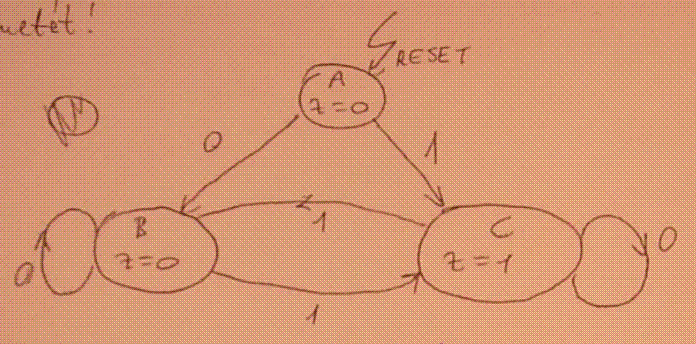
10. Feladat
Adjon egy olyan tesztvektor sorozatot, az alábbi egyetlen X bemenettel rendelkező automatához amely leteszteli az automata összes állapotátmenetét!
| reset | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| X | - | 0 | 0 | 1 | 0 | 1 | - | 1 |
| allapot | A | B | B | C | C | B | A | C |