„Fizika 1 - Ellenőrző kérdések és válaszok” változatai közötti eltérés
| 1 299. sor: | 1 299. sor: | ||
==XX. Fejezet== | ==XX. Fejezet== | ||
===A01. Az ideális gáz állapotegyenlete.=== | |||
=== | |||
pV = nRT | pV = nRT | ||
pV = | pV = NkT | ||
=== | ===A02. A molnyi mennyiség definíciója.=== | ||
<math> \approx 6*10^{23} </math> db részecske. | <math> \approx 6*10^{23} </math> db részecske. | ||
| 1 312. sor: | 1 310. sor: | ||
Egy mól: Bármely anyagból az a mennyiség, ami ugyanannyi elemi részecskét tartalmaz, mint ahány atom található 0,012 kg 12-es C izotrópban. | Egy mól: Bármely anyagból az a mennyiség, ami ugyanannyi elemi részecskét tartalmaz, mint ahány atom található 0,012 kg 12-es C izotrópban. | ||
=== | ===A03. Az ideális gáz kinetikus modellje.=== | ||
# A gáz nagyszámú azonos tömegpontból áll | # A gáz nagyszámú azonos tömegpontból áll | ||
# A részecskék különböző sebességű, véletlen szerű mozgást végeznek, tökéletesen rugalmasan ütköznek egymással és a fallal | # A részecskék különböző sebességű, véletlen szerű mozgást végeznek, tökéletesen rugalmasan ütköznek egymással és a fallal | ||
# Az ütközések során semmilyen más erő nem hat, csak ütközés kölcsönhatásából származó, valamint az ütközés elhanyagolható ideig tart | # Az ütközések során semmilyen más erő nem hat, csak ütközés kölcsönhatásából származó, valamint az ütközés elhanyagolható ideig tart | ||
=== | ===A04. Az átlagos kinetikus energia és a hőmérséklet (egyatomos) ideális gáz estén.=== | ||
<math> \frac{3}{2}kT = \frac{1}{2}m \overline{v}^2 </math> | <math> \frac{3}{2}kT = \frac{1}{2}m \overline{v}^2 </math> | ||
=== | ===A05. A Maxwell-féle sebességeloszlás "diagramja".=== | ||
http://en.wikipedia.org/wiki/Image:MaxwellBoltzmann-en.svg | http://en.wikipedia.org/wiki/Image:MaxwellBoltzmann-en.svg | ||
===B01. Cseppfolyósítható gázok p(V) diagramja és a kritikus pont fogalma.=== | |||
=== | |||
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/fig6VaporDomePV_web.jpg | http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/fig6VaporDomePV_web.jpg | ||
| 1 331. sor: | 1 327. sor: | ||
A kritikus pont felett nem lehet különbséget tenni a folyadék és a gőz állapot között, mivel e pontban a gőz sűrűsége eléri a vele egyensúlyban lévő folyadékfázis sűrűségét. | A kritikus pont felett nem lehet különbséget tenni a folyadék és a gőz állapot között, mivel e pontban a gőz sűrűsége eléri a vele egyensúlyban lévő folyadékfázis sűrűségét. | ||
=== | ===B02. A p(T) fázisdiagram és a hármaspont fogalma.=== | ||
Ahol a három szín találkozik az a hármas pont :) | Ahol a három szín találkozik az a hármas pont :) | ||
http://www.rfcafe.com/references/general/images/p-t_rfcafe.gif | http://www.rfcafe.com/references/general/images/p-t_rfcafe.gif | ||
=== | ===B03. Az ideális gáz állapotegyenletének a levezetése a kinetikus modell alapján.=== | ||
=== | ===B04. A "négyzetes középhőmérséklet" fogalma.=== | ||
=== | ===B05. A "legvalószínűbb sebesség" fogalma és értéke "T" hőmérsékletű ideális gáz esetén.. === | ||
=== | ===B06. A parciális nyomás fogalma. === | ||
A parciális nyomás egy résznyomás, amit akkor fejtene ki a gázelegy adott B komponense, ha az egyedül töltené ki a rendelkezésre álló teljes térfogatot. A B komponens részesedése a rendszer össznyomásából. A komponensek parciális nyomásának összege adja a rendszer össznyomását (Dalton-törvény). | A parciális nyomás egy résznyomás, amit akkor fejtene ki a gázelegy adott B komponense, ha az egyedül töltené ki a rendelkezésre álló teljes térfogatot. A B komponens részesedése a rendszer össznyomásából. A komponensek parciális nyomásának összege adja a rendszer össznyomását (Dalton-törvény). | ||
=== | ===B07. A Maxwell-féle sebességeloszlás matematikai alakja (Tk: 20C-43 feladat)=== | ||
<math>D(v)\,dv = \left ( \frac {m}{2 \pi k T} \right) ^{3/2} 4 \pi v^2 e^{-mv^2/(2kT)}\, dv </math> | <math>D(v)\,dv = \left ( \frac {m}{2 \pi k T} \right) ^{3/2} 4 \pi v^2 e^{-mv^2/(2kT)}\, dv </math> | ||
==XXI. Fejezet== | ==XXI. Fejezet== | ||
A lap 2013. január 23., 19:11-kori változata
Ez az oldal a Fizika 1 tárgyhoz kapcsolódó elméleti kérdések-válaszok gyűjteménye! A Hudson-Nelson könyv fejezeteinek a végén található ellenőrző kérdések közül azok vannak itt, amiket az előadók megoldásra javasoltak.
Szerkesszétek és bővítsétek!
- "A" típusú kérdések: A tananyag legfontosabb, szükséges alapismereteit foglalja össze (ez jelentheti az a tudás "elégséges" szintjét).
- "B" típusú kérdések: A tananyag által megkívánt további ismereteket öleli fel mindez tulajdonképpen a tudásszintet határozza meg.
A ZH-kon és a vizsgákon lényegében ezen ismeretek számonkérése történik. A vizsga harmadik része 5 db. szöveges kifejtést igénylő kérdést tartalmaz, amelyek a ebből kérdésgyűjteményből valók.
II. Fejezet
A01. Az átlagsebesség definíciója egyenes vonalú mozgás esetén.
Átlagsebesség vekor:
A02. A v(t) pillanatnyi sebesség definíciója egyenes vonalú mozgás esetén.
A03. Az átlagos gyorsulás definíciója egyenes vonalú mozgás esetén.
A04. Az a(t) pillanatnyi gyorsulás definíciója egyenes vonalú mozgás esetén.
A05. Az egyenes vonalú egyenletesen gyorsuló mozgás kinematikai egyenletei , azaz x(t), v(t), a(t)
B01. Az x(t) ismeretében határozza meg a v(t) és a(t) függvényeket!
B02. Az a(t) ismeretében határozza meg a v(t) és x(t) függvényeket!
B03. Az x(t), v(t), a(t) függvények közötti kapcsolatok grafikus értelmezése.
Definícióból következik, hogy az x(t) adott pontbeli érintőjének meredeksége az adott pontbeli v(t) értéke. A v(t) grafikon alatti terület pedig megegyezik a megtett úttal, számértékben természetesen. Ugyanez elmondható a v(t) és a(t) kapcsolatáról.
III. Fejezet
A01. A Descartes koordináta-rendszer definíciója (x,y,z).
- _Matekosabb definíció_: feletti vektortér i,j,k ortonormált bázisra illesztett koordináta-rendszer.
- _Szövegesebb definíció_: Három, páronként egymásra merőleges, közös origójú számegyenes Descartes-féle derékszögű, jobbsodrású koordináta-rendszert alkot. A pontnak a koordináta-rendszer síkjaitól mért előjeles távolságát _x_, _y_, _z_ betűkkel jelöljük, ezek a pont derékszögű koordinátái.
A02. A elmozdulásvektor definíciója térbeli mozgások esetén.
A03. Az átlagsebesség és a pillanatnyi sebesség definíciója térbeli mozgás esetén.
A04. Az átlagos gyorsulás és a pillanatnyi gyorsulás definíciója térbeli mozgás esetén.
B01. A henger koordináta-rendszer definíciója.
Két távolsággal és egy szögel definiált vektor:
- _r_: a vektor xy síkbeli vetületének hossza
- _z_: a vektor z tengelyre vett vetületének hossza
- : a vektor xy síkbeli vetületének irányszöge (iránytangense)
Átváltás hengerből Descartes-ba:
B02. A gömbi koordináta-rendszer definíciója.
(Több fajtája is van, a könyvben lévőt írom ide.)
Két szöggel és egy távolsággal definiált vektor:
- _r_: a vektor hossza
- : a vektor xy síkbeli vetületének irányszöge (iránytangense)
- : a vektor a k bázisvektorral bezárt szöge
Átváltás gömbiből Descartes-ba:
B03. A függőleges hajítás.
Általánosságban: Csak a z tengely irányában van elmozdulás, állandó g gyorsulással. Így ez nem más, mint a már fentebb leírt egyenes vonalú egyenletesen gyorsuló mozgás, ahol a = g.
(Az általánosságnak elégnek kell lennie vizsgára, az alábbiak csak a teljesség igénye miatt, ártani biztos nem árt polgárjogon vannak itt!)
Függőleges lefelé hajítás kezdősebességgel:
A test pillanatnyi helyének függőleges koordinátája:
A pillanatnyi sebesség:
Függőleges felfelé hajítás kezdősebességgel:
A test pillanatnyi helyének függőleges koordinátája:
A pillanatnyi sebesség:
Az emelkedés ideje:
Maximális emelkedés:
B05. A ferde hajítás.
Általánosságban: A tér minden irányában történik elmozdulás. Az elmozgás vektora minden esetben felbontható i,j,k bázisvektorokkal párhuzamos összetevőkre, így a továbbiakban elegendő 3 különálló egydimenziós mozgással foglalkozni.
(Itt ugyanaz érvényes, mint az előbb!)
Speciálisan, két dimenzióban: Tegyük fel, hogy az origóból, a vízszintessel szöget bezáró kezdősebességgel hajítunk. Az x irányú sebességkomponens és a pillanatnyi sebességvektor bezárt szöge . Ekkor:
A test pillanatnyi koordinátái:
A pillanatnyi sebesség koordinátái:
A pillanatnyi sebesség nagysága és iránya:
Az emelkedés ideje:
A mozgás teljes ideje:
A hajítás távolsága:
Az emelkedés maximális értéke:
A pálya egyenlete:
B04. A vízszintes hajítás.
Általánosságban: A ferde hajtás egy speciális esete, amikor a kezdeti sebesség vektor Z koordinátája 0.
(Itt is ugyanaz!)
Speciálisan, két dimenzióban: Tegyük fel, hogy az origóból vízszintesen kezdősebességgel hajítunk. Az x irányú sebességkomponens és a pillanatnyi sebességvektor bezárt szöge . Ekkor:
A test pillanatnyi koordinátái:
A pillanatnyi sebesség koordinátái:
A pillanatnyi sebesség nagysága és iránya:
IV. Fejezet
A01. A síkbeli polár koordináták definíciója.
Egy adott _O_ pontból kiinduló félegyenes (polártengely) és egy rá illeszkedő rögzített sík alkotja. E síkban mozgó _P_ pont polárkoordinátái
- a pontban az _O_ pólustól való _r_ távolsága és az
- OP egyenesnek a polártengellyel bezárt szöge.
Átváltás:
A02. A körmozgást végző pont sebességének a grafikus értelmezése.
A sebesség vektor mindig érintő irányú. (Erre gondolt vajon?)
A03. Az egyenletes körmozgást végző pont gyorsulásának a grafikus értelmezése.
Ekkor csak centripetális gyorsulása van, ami a kör középpontja felé mutat, ez a gyorsulás tartja körpályán a testet.
A04. A nem egyenletes körmozgást végző pont gyorsulásának a grafikus értelmezése.
Ekkor a test gyorsulásának van egy tangenciális (érintővel párhuzamos) és egy centripetális összetevője (ami a kör középpontja felé mutat).
B01. Az és az egységvektorok időderiváltjai.
(Könyv jelölései: és )
B02. Az általános körmozgást végző tömegpont sebessége polárkoordinátákkal.
B03.Az általános körmozgást végző tömegpont gyorsulása polárkoordinátákkal.
B04. Általános, görbe vonalú mozgás sebessége.
B05. Általános, görbe vonalú mozgás gyorsulása.
B06. A térbeli pálya görbületi sugarának a definíciója.
Egy pálya görbéjének minden egyes pontjához illeszthető simuló (görbületi) kör, ennek sugara a görbületi sugár. (Matematikában a simulókör görbülete a simulókör sugarának reciproka.)
V. Fejezet
A01. Newton első axiómája és az ezzel kapcsolatos megfigyelések és kísérletek.
Létezik olyan inerciarendszer, melyben minden test nyugalomban marad vagy egyenes vonalú egyenletes mozgást végez mindaddig, míg ezt az állapotot egy másik test vagy mező meg nem változtatja. Megfigyelések és kísérletek:
- A csillagközi térben mozgó protonra lényegében nem hat erő, így megtartja egyenes vonalú egyenletes mozgását.
- Ha úgy húzunk egy kocsit, hogy az erő csak a súrlódást egyenlít ki, akkor a kocsi megtartja egyenes vonalú egyenletes mozgását.
A02. Newton második axiómája és az ezzel kapcsolatos megfigyelések és kísérletek.
Egy pontszerű test 'a' gyorsulása egyenesen arányos a testre ható, a gyorsulással azonos irányú 'F' erővel, és fordítottan arányos a test 'm' tömegével. Ennek két változata él:
- a klasszikus:
- és a relativisztikusan is alkalmazható:
Megfigyelések és kísérletek:
- Ugyanakkora rúgás mást okoz a focilabdának és mást az ólomgolyónak, mert az ólomgolyónak más a tömege. A tömeg definíciója a mozgásállapot-változtató hatással szemben tanúsított ellenállás. Itt a mozgásállapot-változtató hatás értelemszerűen a rúgás, ezzel szemben az ólomgolyónak nagyobb az ellenállása.
- Nyilván, lehet akkorát rúgni az ólomgolyóba, hogy ugyanoda repüljön, mint a focilabda.
A03. Newton harmadik axiómája és az ezzel kapcsolatos megfigyelések és kísérletek.
Ha egy testre egy másik test F erővel hat, akkor a második test az első testre ugyanekkora nagyságú, ellentétes irányú ellenerővel hat. Megfigyelések és kísérletek:
- Nyomóerő - tartóerő.
- Autó gyorsítása: a kerék "hátrafelé löki" a talajt, az pedig "előrenyomja" a kerekeket.
A04. Az erőhatások szuperpozíciója (Newton "negyedik axiómája" - Stevin-tétel) és az ezzel kapcsolatos megfigyelések és kísérletek.
Az erő vektormennyiség, azaz vektorként adódnak össze és vektorként szorzódik skalárral. Megfigyelések és kísérletek:
- Kötélhúzás.
- Lejtőn lecsúszó test.
A05. Az impulzus definíciója.
B01. A "húzó" (illetve "nyomó") erő.
Olyan erők, melyek egy közeg atomjait egymástól távolítják, vagy közelítik. A húzó- illetve nyomóerő különböző testek között közvetíthető elhanyagolható tömegű kötél illetve rúd segítségével. (Ha van valakinek elfogadott válasza erre, írja fel!)
B02. A "rugóerő".
Hooke-törvény: ahol _k_ az adott rugóra jellemző rugóállandó és _r_ a kitérés az egyensúlyi állapottól.
B03. A "súrlódási erő".
B04. A testek tömege és a súlya.
- Tömeg: _m_, a mozgásállapot-változtató hatással szembeni ellenállás mérőszáma.
- Súly(erő): _G_, az az erő, mellyel egy test az alátámasztást nyomja, vagy a felfüggesztést húzza.
VI. Fejezet
A01. Az állandó nagyságú erő munkája.
Az F erő W munkája megegyezik az erő elmozdulás irányába eső komponensének és az elmozdulás nagyságának szorzatával. vagy ahol s: elmozdulás.
Mértékegysége: [W] = Nm = J (joule).
A02. A gravitációs erő munkája.
Ha a mozgás során g állandó: ahol:
- _h_: magasság
- _m_: a test tömege
- _g_: gravitációs gyorsulás
Ha nem tekinthetjük g-t állandónak:
_A_ és _B_ pontok között:
ahol
- a gravitációs állandó
- _A_ és _B_ a kép pont, melyek között a mozgás történik, és ezen pontok helyvektorai
- _m_ a vizsgált test tömege, _M_ pedig a gravitációs teret keltő test tömege
A03. A változó nagyságú erő munkája.
_A_ és _B_ pontok között:
A04. A rugóerő munkája.
ahol
- _k_: a rugóra jellemző rugóállandó [N/m]
- _x_: a kitérés
A05. A munkatétel.
vagy
A06. A potenciális energia definíciója.
ahol a viszonyítási pont helyvektora. Az az energia, amellyel egy test rendelkezik konzervatív erőtérben.
Konzervatív erőtér: (ekvivalens definíciók)
- Olyan erőtér, mely forrásos és örvénymentes.
- Olyan erőtér, melyben ható erő - a konzervatív erő - munkája csak a pálya kezdő-, és végpontjától függ, vagyis független a pálya alakjától.
- Olyan erőtér, melyben ható erő - a konzervatív erő - bármely zárt görbén végzett összes munkája nulla, vagyis
A07. A pillanatnyi teljesítmény definíciója.
B01. A munkatétel levezetése.
Tekintsük a hely függvényében változó F(x) erőt. Az ilyen eredő erő hatására x = a -tól _b_ -ig elmozduló testen a munkavégzés: Tudjuk, hogy . Alkalmazzuk a deriváltra a (lejjebb található) 1. összefüggést (a láncszabályt): és helyettesítsük be az eredményt az egyenletbe. Azt kapjuk, hogy Így a méglejjebb található 2. összefüggés felhasználásával a következőt kapjuk:
A fent használt összefüggések:
- A láncszabály:
B02. A súrlódási erő munkája.
B03. A munkatétel és a potenciális energia.
B04. A hatásfok definíciója.
VII. Fejezet
A01. A konzervatív erõk definíciója.
Ekvivalens definíciók:
- A konzervatív erő munkája csak a pálya kezdő-, és végpontjától függ, vagyis független a pálya alakjától.
- A konzervatív erő bármely zárt görbén végzett összes munkája nulla, vagyis
A02. A potenciális energia és a konzervatív erő.
Ekvivalens megfogalmazások:
- Az az energia, amellyel egy test rendelkezik konzervatív erőtérben.
- Az a munkamennyiség, amely ahhoz szükséges, hogy a testet (vagy töltést) a potenciális energia 0 szintjéről egy adott helyre mozgassunk.
A03. A mechanikai energia megmaradásának a tétele.
Ha csak konzervatív erők hatnak:
A04. Az energia megmaradásának az (általános) tétele.
B01. Példák nem konzervatív erőkre.
Nem konzervatív, vagyis disszipatív erők.
- Súrlódási erő
- Bármely időtől vagy a tömegpont sebességétől függő erő
B02. Példák a mechanikai energiamegmaradás tételére.
- Egy töltéssel rendelkező fém golyó gurul lefelé egy súrlódásmentes lejtőn és egy rugónak csapódik. Miközben lökődik vissza a rugóról odateszünk egy azonos töltésű részecskét és eltaszítjuk egy homogén mágneses térbe, így körpályán kering az idők végezetéig. Az egész jelenség természetesen vákuumban játszódik le. (Megjegyzés: ez jópofa, ezért bennhagytam, de helytelen, ugyanis a gyorsuló töltés elektromágneses sugárzást bocsájt ki!)
- Tökéletesen rugalmas ütközés.
B03. Példák az energiamegmaradás (általános) tételére.
- (Most nem súrlódásmentes) lejtőn leguruló testre ráfingik egy lepke (közegellenállás).
- Ütközés: a jelentősen lecsökkenő mozgási energia fedezi az ütköző testek deformációját, bizonyos mennyiségű hő is keletkezik.
- Égés: az anyagon belüli molekuláris kötésekben tárolt (kémiai) energia szabadul fel hő-, fény-, hang-, satöbbi energiává, miközben az anyag is átalakul (A dieselből lesz korom, szén-, és nitrogénoxidok, stb.)
B04. Az energiamegmaradás tétele a fizikában (mikro- és makroszkopikus szinten).
Egy test belső energiájának megváltozása egyenlő a testtel közölt hő és a rajta végzett térfogati munka összegével:
VIII. Fejezet
A01. Az impulzus megmaradás tétele.
Két test kölcsönhatásánál az egyes testek sebességei úgy aránylanak egymáshoz, mint a tömegeik, következésképpen tömegük és sebességváltozásuk szorzata megegyezik. A hatás-ellenhatás elve alapján feltételezhetjük, hogy a dinamikai párkölcsönhatásban a két testet azonos ideig ugyanolyan nagyságú hatás éri, következésképpen dinamikai jellemzőik is azonos mértékben változnak. Amennyiben a két test által alkotott rendszert zártnak tekinthetjük, fentiek alapján kijelenthető, hogy a zárt rendszerben a lendületváltozások vektori összege 0, vagyis a rendszer össz lendülete állandó.
A02. Az "erőlökés" ("erőimpulzus") fogalma.
Az erőlökés a testekre kifejtett mozgásállapot-változtató hatást jellemzi. Egyenesen arányos
- a testre ható erővel
- az erőhatás időtartamával
Az erőlökés megegyezik a lendületváltozással.
A03. A "rakéta mozgás" elve.
A rakéta testének és a kiáramló hajtógázoknak az összes impulzusa állandó, így a "hátrafelé" kiáramló gázok impulzusa megegyezik a rakétatest impulzusával.
B01. Az impulzus megmaradás tételének a levezetése.
2 tömegpontra: például 2 golyó ütközik.
Az egymásra ható erők Newton 3. törvénye értelmében megegyeznek: , így:
Tehát az impulzusok vektori összege az ütközések során nem változik, egy időtől független állandó. Ez kiterjeszthető tetszőleges zárt rendszerre:
ahol a 0 index a kezdeti értéket, az index hiánya pedig a tetszőleges _t_ időponthoz tartozó értéket jelöli.
B02. Példák az impulzus megmaradás tételére.
- Rakétamozgás.
- Rugalmas és rugalmatlan ütközés.
B03. A rakéta mozgás részletes matematikai tárgyalása.
Hozzávalók:
- Földhöz rögzített viszonyítási rendszer
- a _t_ időpontban:
- _v_ a rakéta sebessége
- _m_ a rakéta tömege
- a időpontban:
- a rakéta kiáramló hajtóanyag hatására megnövekedett sebessége
- a rakéta kiáramló hajtóanyag miatt lecsökkent tömege
- a hajtóanyag kiáramlásának sebessége
- a kiáramlott hajtóanyag tömege
- _g_ állandó
Vegyük észre a következőket:
- tehát a kibocsájtott üzemanyag Földhöz képesti sebessége egyenlő a rakéta Földhöz képesti sebessége mínusz a hajtóanyag rakétához viszonyított sebessége.
- vagyis értelemszerűen ahogy halad a rakéta, úgy csökken a tömege, mivel bocsájtja ki a hajtóanyagot, tehát növekszik a kibocsájtott hajtóanyag-mennyiség.
Írjuk fel Newton II. törvényét a következő formában:
Mivel a "Vegyük észre..." pontban észrevettük a 2. pontot, ezért tudjuk:
Mivel , így , valamint , tehát , így a rakéta gyorsulása:
A rakéta sebességének meghatározása, ha időben nyugalomból indul integrálással:
B04. Szabadon (gravitáció mentes térben) mozgó rakéta maximális sebessége.
Az előző pontban elkövetett levezetés eredményét felhasználva rögtön látszik a megoldás:
Gravitáció nélkül ennyi maradt. Látható, hogy a maximális sebességet kétféleképpen lehet növelni:
- a rakéta kezdeti tömegének és a minden üzemanyag elégetése utáni üres tömegének hányadosa legyen minél nagyobb és
- a hajtóanyag minél nagyobb sebességgel áramoljék ki a fúvókákon.
B05. Példák folytonosan változó tömegű rendszerek impulzusára.
- Szállítószalag, melyre árut öntenek.
- Egy lánc, amit lassan a földre eresztünk.
IX. Fejezet
A01. A rugalmas ütközés definíciója.
Rugalmas ütközés esetén a vizsgált részecskerendszer tagjainak összes kinetikus energiája az ütközés után és előtt megegyező. Tehát a mechanikai energia és a lendületmegmaradás is érvényes.
A02. A rugalmatlan ütközés definíciója.
Ha az ütközés során a kinetikus energia egy része "elvész" (például hővé alakul, vagy deformálódik a test), akkor rugalmatlan ütközésről beszélünk. Itt tehát a mechanikai energia megmaradás nem érvényesül, csak a lendületmegmaradás.
A03. A tömegközéppont definíciója két részecske esetén.
A04. A tömegközéppont tétele két részecske esetén.
A TKP úgy mozog, mintha oda összpontosulna a két részecske együttes tömege, és rá a külső erők vektori összege hatna.
A05. A tömegpontrendszer definíciója.
Az , , ... helyeken található , , ... tömegű pontszerű testek pontrendszert alkotnak.
B01. A tömegközéppont definíciója "N" db. részecskéből álló tömegpontrendszer esetén.
B02. A tömegközéppont tétele "N" db. részecskéből álló tömegpontrendszer esetén.
A TKP úgy mozog, mintha benne a rendszer teljes _M_ tömege egyesítve lenne, és rá a külső erők vektori összege hatna.
B03. Newton második törvénye "N" db. részecskéből álló tömegpontrendszer esetén.
B04. A tömegpontrendszer impulzusa.
B05. A tömegpontrendszer kinetikus energiája.
B06. Kétrészecskés ütközések leírása tömegközépponti koordináta-rendszerben.
A TKP nem mozog >> p = 0 Így egyszerűbb a számítás.
B07. Ütközések osztályzása: rugalmas, centrális, egyenes ütközések definíciója.
- Rugalmas: a mechanikai energia és a lendület is megmarad.
- Centrális: az ütközési ponton a két test felületének normál vektora a másik test tömegközéppontjába mutat. (Vagyis "telibe" kapják egymást, nem csak a szélük találkozik.)
- Egyenes: a sebességvektorok párhuzamosak.
B08. Az "ütközési paraméter" fogalma.
Vegyünk merev, kiterjedt testeket, melyek közül az egyik mozdulatlan, a másik _v_ sebességgel halad felé. A mozgó test sebességvektora és az álló test tömegközéppontján áthaladó, a sebességvektorral párhuzamos egyenes távolsága az ütközési paraméter. Ha az ütközési paraméter zérus, akkor centrális ütközésről beszélünk. ahol
- az ütközési paraméter
- és a sebességek
- és a kezdeti koordináták
- a relatív sebesség
X. Fejezet
A01. A forgatónyomaték(vektor) definíciója.
A02. A merev test definíciója.
A merev test részecskéi megtartják egyméshoz viszonyított helyzetüket.
A03. A merev test tömegközéppontja ("súlypontja").
A04. A merev test egyensúlya.
B01. A merev test egyensúlyának típusai.
- Stabilis: innen kimozdítva a test visszaáll eredeti helyzetébe, pl. kelj fel Jancsi.
- Instabil (labilis): nem áll vissza ugyanoda, egy másik egyensúlyi pontba mozdul tovább, pl. kártyavár.
- Semleges: picit elmozdítva egy másik egyensúlyi helyzetbe kerül, pl. vízszintes felületen egy golyót odébb gurítunk.
XI. Fejezet
A01. Az átlagos- és a pillanatnyi szögsebesség.
A02. Az átlagos- és a pillanatnyi szöggyorsulás.
A03. A körmozgást végző pont kerületi- és szögsebessége közötti kapcsolat.
A04. A körmozgást végző pont centripetális gyorsulása és a szögsebesség.
A05. A körmozgást végző pont tangenciális gyorsulása és a szöggyorsulás.
B01. A forgó mozgás kinematikai egyenletei
Az átlagos szögsebesség definíciójából:
B02. A forgó mozgás kinematikai egyenleteinek levezetése.
Állandó esetén mindkét oldalt integrálva
Elvégezve az integrálást:
Mivel , így:
Integrálva:
Elvégezve az integrálást:
Tehát:
A másik két kinematikai egyenlet az átlagos szögsebesség definíciójából következik.
B03. A gördülő kerék mozgásának jellemzése.
Csúszás nélküli, tehát a TKP sebessége megegyezik a forgás kerületi sebességével:
Haladó mozgásra felírható egyenlet:
Forgó mozgásra felírható egyenlet:
TKP egyensúlyban van:
A fenti öt egyenlet egyértelműen jellemzi a mozgást.
XII. Fejezet
A01. A merev test adott tengelyre vett tehetetlenségi nyomatékának a definíciója.
A könyv I-vel jelöli, így a továbbiakban én is ezzel fogom
A02. A perdület (impulzusmomentum) vektor definíciója.
_v_ sebességgel mozgó, _m_ tömegű pontnak adott _O_ pontra vonatkozó perdületén (impulzusnyomatékán, impulzusmomentumán, mozgásmennyiségének nyomatékán) lendületének az _O_ pontra vonatkozó nyomatékát értjük.
ahol _r_ az _O_ pont és az _m_ tömegpont távolsága.
Nagysága:
ahol _k_ az impulzusvektor "karja", vagyis az impulzusvektor egyenesének és az _O_ pontnak a távolsága.
Szimmetriatengelyük körül forgó szimmetrikus testekre:
Perdülettétel:
Ha a forgatónyomaték változó, és időpontok között:
A03. A forgó mozgás alapegyenlete.
A04. Az impulzusmomentum megmaradásának a tétele.
A05. A munkatétel rögzített tengely körül forgó merev test esetén.
B01. Homogén pálca tehetetlenségi nyomatékának a számítása.
Tömör, homogén henger _r_ sugárral, _m_ tömeggel és _h_ magassággal:
http://upload.wikimedia.org/wikipedia/commons/8/84/Moment_of_inertia_solid_cylinder.png
Ha a henger valamelyik paramétere a feladat szövege szerint elhanyagolható, akkor értelemszerűen 0-ként vesszük figyelembe (például itt a "pálca" szóból lehet gondolni, hogy .)
B02. Tömör, homogén henger szimmetriatengelyére vett tehetetlenségi nyomatékának a kiszámítása.
Lásd egyel feljebb!
B03. A szögsebesség vektor definíciója.
XIII. Fejezet
A01. Newton-féle mozgásegyenlet (kiterjedt) testek mozgása esetén.
!A02. Az impulzusmomentum tétele (kiterjedt) testek mozgása esetén.
Egy test tömegközéppontra vett impulzusmomentumának változási sebessége egyenlő a tömegközéppontra vett külső forgatónyomatékok erdőjével, még akkor is, ha a test tömegközéppontja - a gyorsulást is beleértve - elmozdul.
A03. A Steiner-tétel.
A tehetetlenségi nyomaték definíció szerint függ a tengely megválasztásától. A szimmetriatengellyel egybeeső forgástengelyek ismeretében az ezzel párhuzamos tengelyekre vonatkoztatott tehetetlenségi nyomatékok közötti összefüggést a Steiner-tétel adja meg:
ahol
- _m_ a test össztömege
- _d_ a párhuzamos tengelyek távolsága
- a tömegközépponton átmenő tengelyre vonatkozó tehetetlenségi nyomaték
- a tömegközépponton átmenő tengellyel párhuzamos, attól _d_ távolságra vélő forgástengelyre vonatkozó tehetetlenségi nyomaték
A04. Az erőpár fogalma
Két erő, melyek hatásvonala párhuzamos, egy síkban vannak és ellentétes irányúak, erőpárt alkotnak. Ez a legelemibb erőrendszer, ami nem írható fel egyetlen eredő erővel.
B01. A pörgettyű precessziója.
"Az L impulzusmomentum vektor követni igyekszik az _M_ forgatónyomaték vektor irányát"
B02. A pörgettyűs iránytű működése.
Lásd itt!
XIV. Fejezet
A01. Tehetetlenségi erő transzlációs (egyenesvonalú) gyorsulást végző koordináta-rendszerekben.
Ha a koordináta-rendszer gyorsulása :
A02. A centrifugális erő forgó koordinátarendszerekben.
Mindig a forgástengelyre merőlegesen kifelé mutat.
A03. A Coriolis erő forgó koordinátarendszerekben.
Ha a test forgó koordinátarendzserben nem mozog, akkor nincs Coriolis erő.
Az északi féltekén jobbra, a déli féltekén balra tereli el a mozgást.
B01. A Foucault inga.
Lásd itt!
B02. A ciklonok kialakulása.
A Coriolis erő az északi féltekén mozgó légtömegeket jobbra téríti el. Ha egy alacsony nyomású tartomány a környező légtömegeket vonzani kezdi, akkor a Coriolis eltérítés az óramutató járásával ellentétes irányú "örvényt", cikont hoz létre.
XV. Fejezet
A01. Az egyszerű (egydimenziós) harmonikus rezgő mozgás mozgásegyenlete.
A02. Az egyszerű harmonikus rezgő mozgás mozgástörvénye.
Hooke törvény:
A03. Az energia megmaradás tétele egyszerű harmonikus rezgő mozgás esetén.
A04. A fonálinga (matematikai inga) mozgásegyenlete.
Kis kitérések esetén (Értelmezés sikertelen (formai hiba): {\displaystyle \theta \leq 5° } ):
ahol
- a szögelfordulás
- _g_ a gravitációs gyorsulás
- _l_ a fonál hossza
A lengésidő kis kitérések esetében:
A05. A fizikai inga mozgásegyenlete.
Kis kitérések esetén (Értelmezés sikertelen (formai hiba): {\displaystyle \theta \leq 5° } ) igaz, hogy :
ahol
- _l_ a felfüggesztési pont távolsága a test tömegközéppontjától.
- _g_ a gravitációs gyorsulás
- _M_ a forgatónyomaték
- _I_ a tehetetlenségi nyomaték
Lengésidő kis kitésérek esetén:
A06. A csillapított rezgőmozgás mozgásegyenlete.
ahol
- _m_ a rezgő test tömege
- _b_ a csillapítási tényező
- _k_ a rugóállandó
Ha a csillapítás kicsi, tehát , akkor az x(t) függvény:
ahol a fentiek mellett
Az amplitúdó időfüggvénye:
A07. Az alulcsillapított rezgőmozgás mozgástörvénye.
ha
A08. A gerjesztett rezgőmozgás mozgásegyenlete.
ahol
- _m_ a rezgő test tömege
- _b_ a csillapítási tényező
- _k_ a rugóállandó
- a gerjesztő erő
A09. A rezonancia fogalma.
Rezonancia (magyarul együttrezgés) akkor jön létre, ha a kényszerítő rezgést végző test frekvenciája megegyezik a kényszerrezgést végző test sajátfrekvenciájával. Rezonancia esetén a kényszerrezgést végző test amplitúdója a más frekvenciákon történő kényszerrezgéseknél előálló amplitúdókhoz képest a lehető legnagyobb. Amennyiben ez a megnövekedett amplitúdó eléri az adott anyag deformálhatóságának a határát, bekövetkezik a rezonanciakatasztrófa. A rezonancia jelenségére és a rezonanciakatasztrófára példa az Amerikai Egyesült Államok Washington államában lévő Tacoma Narrows Bridge 1940-es összeomlása. A függőhíd szerkezete nem bírta a ki a szél által keltett lökéshullámokat, és az útpálya beszakadt.
B01. Az egyszerű (egydimenziós) harmonikus rezgő mozgás mozgásegyenletének a megoldása.
Lásd: A01. és A02.
B02. A fonálinga (matematikai inga) mozgásegyenletének a megoldása.
Lásd: A04.
B03. A torziós inga mozgásegyenlete.
Fentieket egyesítve:
ahol a torziós rugóállandó
B04. A torziós inga mozgásegyenletének a megoldása.
megoldása:
ahol a mozgás szögamplitúdója radiánban.
Lengésidő:
B05. A fizikai inga mozgásegyenletének a megoldása.
Lásd A05.
B06. A mozgástörvény kritikus csillapítás esetén.
Kritikus csillapítás esetén a csillapítási tényező .
B07. A mozgástörvény túlcsillapítás esetén.
Túlcsillapítás esetén a csillapítási tényező ..
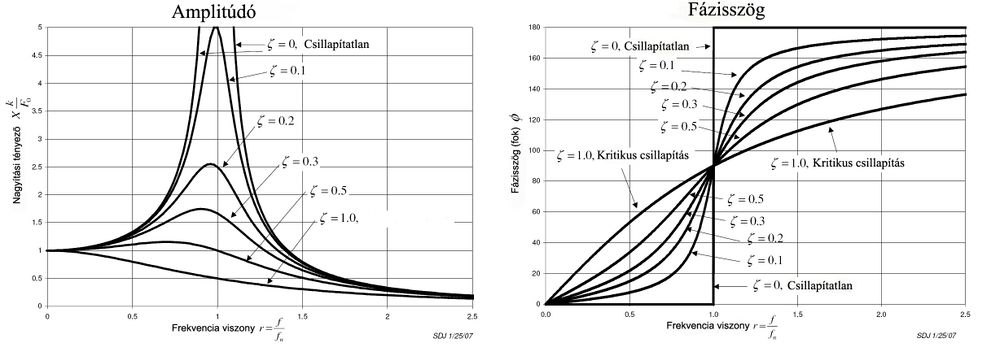
B08. A kényszerrezgés amplitúdó-frekvencia függvényének a grafikonja.
B09. A kényszerrezgés fáziskésés-frekvencia függvényének a grafikonja.
Lásd: B08.
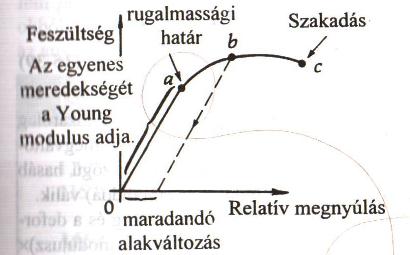
B10. A rugalmas anyagok "feszültség-megnyúlás" diagramja.
B11. A "húzó-" és a "nyírófeszültség" definíciója.
- Húzófeszültség: az erő merőleges a felületre.
- Nyírófeszültség: az erő a felület legfelső rétege mentén érintőlegesen hat.
B12. A "deformáció" fogalma és fajtái.
Az anyag feszültség hatására bekövetkező alakváltozása. Fajtái:
- Hosszirányú deformáció: húzó feszültség hatására (ld. B11.).
- Térfogati deformáció: a test térfogati változász szenved, de alakja megmarad.
- Nyírási deformáció: nyírófeszültség hatására (ld. B11.).
XVI. Fejezet
A01. Newton tömegvonzási törvénye
Bármely két részecske között fellépő vonzóreő:
ahol
- a gravitációs állandó
- _r_ a részecskék közötti tavolság
- _m_ és _M_ a kölcsönhatásban résztvevő testek tömegei
Vektoriális alakban:
A02. A centrális erő fogalma
Olyan vonzó vagy taszító erő, melynek hatásvonala mindig egy rögzített ponton megy át, például a gravitációs erő, amit a Nap gyakorol a Földre.
A03. Tömegpont impulzusmomentuma centrális erőtérben
A centrumra vonatkoztatott imulzusmomentum megmarad.
(Centrális erőtér: olyan erőtér, amelyben mindig található egy pont (erőcentrum), amelyen minden az erőtérhez tartozó erő hatásvonala átmegy.)
A04. A gravitációs térerősség.
A gravitációs térerősség a _g_ nehézségi gyorsulás:
_M_ tömegponttól származó gravitációs térerősség
A05. A gravitációs potenciális energia definíciója.
ahol
- a gravitációs állandó
- _m_ a vizsgált test tömege, _M_ pedig a gravitációs teret keltő test tömege
B01. A szökési sebesség fogalma
Az a legkisebb kezdeti sebesség mellyel a Föld felszínéről indított test úgy hagyhatja el a Földet, hogy soha nem tér vissza.
B02. A gravitációs térerősség homogén tömör gömb esetén
A gömbszimmetrikus tömegeloszlású, gömbalakú testen kívül lévő _m_ tömegű részecskére a gömb által ható gravitációs erő ugyanolyan, mintha a gömb tömege a középpontban lenne koncentrálva.
B03. A gravitációs térerősség homogén gömbhéj esetén
Az a gravitációs erő, amit a homogén gömbhéj a belsejében tetszés szerinti helyen lévő részecskére gyakorol, zérussal egyenlő.
B04. A gravitációs potenciális energiafüggvény homogén tömör gömb esetén.
ahol
- a gravitációs állandó
- _r_ a részecskék közötti tavolság
- _m_ és _M_ a kölcsönhatásban résztvevő testek tömegei
B05. A Kepler törvények
- A bolygók olyan ellipszispályán keringenek, amelynek egyik gyújtóponjában a Nap van.
- A Naptól a bolygóhoz húzott sugár egyenlő időközök alatt egyenlő területeket súrol.
- A keringési idők négyzetei úgy aránylanak egymáshoz, mint a nagytengelyek köbei, azaz pl.:
B06. A mesterséges hold pályája és energiája közötti kapcsolat.
Mesterséges hold energiája:
- Amennyiben E < 0, úgy ellipszis pályán mozog a szatellit, melynek egyik gyújtópontjában a Föld áll.
- Amennyiben E = 0, úgy parabola pályán mozog a szatellit, a test sebessége végtelenben 0-hoz tart.
- Amennyiben E > 0, úgy hiperbola pályán mozog a szatellit, elhagyja a Földet.
XVII. Fejezet
K I M A R A D
XVIII. Fejezet
A01. A rugalmas hullámok osztályozása.
- Transzverzális hullám: közeg részecskéi a hullám haladási irányra merőlegesen rezegnek.
- Longitudinális hullám: közeg részecskéi a hullám haladási irányval párhuzamosan rezegnek.
A02. Az egydimenziós hullámegyenlet.
A03. Az (egydimenziós) hullámegyenlet általános megoldása.
A04. Az (egydimenziós) harmonikus hullámfüggvény
A05. A hullámszám és a hullámhossz.
Hullámszám:
Hullámhossz:
A06. A fázissebesség fogalma.
A kifeszített húron haladó transzverzális hullám terjedési sebessége: ahol
- _F_ a húrt feszítő erő
- a hosszegységre jutó tömeg - lineáris tömegsűrűség
A07. Az (egydimenziós) állóhullám.
Rögzített végű kötél esetén:
Legyen _l_ a kötél hossza, így a visszavert hullám (fázisugrást szenved):
Összemasszírozva:
Csomópont van, ha:
Speciális eset, ha a hullám önmagába megy át:
Állóhullámok, N = 1 az alapharmónikus, N > 1 felharmónikusok
A08. A Doppler effektus.
B01. A megfeszített kötélen érvényes (egydimenziós) hullámegyenlet levezetése.
Hozzávalók:
- _x_: a lökéshullám terjedési irányába mért koordináta
- _y_: a kötél részecskéinek kitérése az egyensúlyi helyzetből
- : a kötél lineáris tömegsűrűsége
- : a kötél adott szakasza által meghatározott egyenes és az egyensúlyi állapotban lévő kötél hajlásszöge
Vegyük észre, hogy:
- ...mivel a kötél lineáris tömegsűrűsége, így egy hosszúságú szakaszának tömege .
- ...
Feltételezéseink:
- A szög mindig kicsi
- Az _y_ irányú kitérés mindig elég kicsi ahhoz, hogy a folyamat során az _F_ erő ne változzék
Az 1. feltételezésünk miatt:
A kötélszakaszra a következő függőleges irányú erő hat:
Értelmezés sikertelen (formai hiba): {\displaystyle F_{eredő_{transz}} = F \sin(\theta + \Delta \theta) - F \sin\theta }
Vagyis az előző kettőt egyesítve:
Értelmezés sikertelen (formai hiba): {\displaystyle F_{eredő_{transz}} = F \left[ \left( \frac{\partial y}{\partial x} \right)_{x + \Delta x} - \left( \frac{\partial y}{\partial x} \right)_{x} \right] }
Mivel:
így a fentiekből a következőt kapjuk:
Értelmezés sikertelen (formai hiba): {\displaystyle F_{eredő_{transz}} = F \left( \frac{\partial^2y}{\partial x^2} \right) \Delta x }
Newton II. törvényét a transzverzális mozgásra () és a fenti "Vegyük észre..." 1. pontját figyelembe véve a következőt állíthatjuk:
Átrendezgetve:
A fenti, és a "Vegyük észre..." 2. pontja alapján pedig kijön a hullámegyenlet:
B02. A rugalmas transzverzális hullámok (fázis)sebessége.
G: nyírási modulusz
B03. A rugalmas longitudinális hullámok (fázis)sebessége.
K: kompresszió modulusz
B04. A gázokban terjedő hullámok (fázis)sebessége.
B05. A hullámfront fogalma.
A hullámfront minden egyes pontja azonos fázisban van (2-3D-s hullámokra van értelme).
B06. A sík-, henger- és gömbhullámok.
A04-es egyenletet ki lehet egészíteni y és z koordinátákra, így 2 ill 3 D-s hulláokat kapunk.
B07. A "decibel" skála.
I helyére bármilyen mennyiség kerülhetne, speciálisan hullámokra I az intenzitás, pedig nemzetközi referencia szint . A hányadosnak és az lg-nek nincs mértékegysége, így a 10-re rá szoktunk akasztani egy dB mértékegységet, jól látszik azonban, hogy így ez nem lesz SI beli.
B08. A síkbeli hanghullám energia-áramsűrűsége.
B09. Hullámok visszaverődése (peremfeltételek).
A húr mentén terjedő hullámok a húr rögzített végéről 180°-os fázisváltozással (ld. A07.), szabad végről azonos fázisban verődnek vissza.
B10. A Mach-kúp nyílásszöge lökéshullámok esetén
A kúp félnyílásszögének színusza:
B11. A lebegés frekvenciája.
Egy és egy körfrekvenciájú hullám találkozik, és a két körfrekvencia közti eltérés elég kicsi.
Jól látszok a fenti függvényből, hogy a rezgés frekvenciája lesz, amit egy alacsony () rezgésszámú szinusz hullám modulál.
XLI. Fejezet
A01. A Galilei transzformáció
Legyen az x tengely mentén mozgó (vesszős) koordinátarendszer sebessége a referenciához képest V. Ekkor:
A02. Az esemény fogalma
egy esemény: (x,y,z,t)
A03. Az Einstein-féle relativitáselmélet posztulátumai
- A fizika minden törvényének ugyan az a matematika alakja minden inerciarendszerben
- A vákuumbeli fénysebesséég értéke ugyan az minden inerciarendszerben
A04. A Lorentz transzformáció
A05. A relativisztikus impulzus
A relativisztikus tömeg:
A06. A relativisztikus energia
B01. Az idődilatáció
B02. Az ikerparadoxon
Kér ikertesó közül az egyik egy közel fénysebességgel haladó ürhajóval járja be az univerzumot, számára a Földihez ékpest sokkal lasabban tellik az idő. Amikor visszaér a testvére már öreg és földig ér a szakálla, míg az utazó csak pár évvel idősebb.
B03. Az egyidejűség
Az egyidejűség relativitása azt mondja ki, hogy az egyidejűség nem abszolút, hanem függ a megfigyelő helyzetétől.
B04. A hosszkontrakció
B05. A relativisztikus sebességösszeadás
B06. A relativisztikus Doppler effektus
Távolodó fényforrás: Közeledő fényforrás:
B07. Az általános relativitáselmélet alapposztulátuma
- A természet törvényei megfogalmazgatóak úgy, hogy tetszőleges tér-idő vonatkoztatási rendszerben bármely megfigyelő szerint azonos matematikai alakúak legyenek (akár gyorsuló vonatkoztatási rendszerben is)
- Tetszőleges pont közelében a gravitációs tér minden tekintetben egyenértékű egy olyan gyorsuló vonatkoztatási rendszerrel, amelyben nincs gravitáció.
XIX. Fejezet
A01. A hőmennyiség fogalma és mértékegysége.
A rendszer és környezete között - kizárólag hőmérsékletkülönbség következtében - kicserélődő energia.
Mértékegysége: kalória (cal); 1 cal = 4,184 J
A02. A (termikus) belső energia fogalma
Atomok és molukulák potenciális és kinetikus energiájából adódó energia.
A03. A (fajlagos, moláris) hőkapacitás
- Fajhő:
- Mólhő:
A04. Az átalakulási hő ("látens hő") fogalma és mértékegysége.
A fázisátalakulás során átvitt hőmennyiség. Mértékegysége:
Egyébként pedig
ahol _L_ a látens hő.
A05. A hővezetés alapegyenlete.
A06. A gázhőmérő.
A gáz nyomása az a termometrikus tulajdonság, ami hőmérséklet meghatározására alkalmas.
Hudson-Nelson 472. oldal 19-17 ábra
A gáz megtartja térfogatát, de a nyomása megváltozik. A nyomást a két higanyoszlop közötti _h_ magasságkülönbségből számolhatjuk ki.
B01. A lineáris hőtágulási együttható fogalma
Arányossági tényező, megmutatja, hogy 1 fok hőmérséklet növekedés hatására milyen arányban nyúlik meg a test hossza.
B02. A kristályos, szilárd testek lineáris hőtágulásának mikrofizikai oka
Az anyagok melegedése során a molekuláris mozgás egyre hevesebb. Szilárd testben a szomszédos atomok közt működő erők potenciális energia-függvény segítségével adhatók meg. Hőm. növekedésével egyre nagyobb potenciális energiára tesznek szert az atomok. De a potenciális energia görbe nem szimmetrikus, azaz nagyobb távolságban kisebb erő húzza vissza az atomot, mint ami a közelben ellőki. Tehát több időt tölt magyobb távolságban, így átlagban tágulni fog a test. (Ha szimmetrikusan rezegne tovább, csak nagyobb amplitúdóval, attól még átlagosan ugyan annyi maradna.)
B03. A térfogati hőtágulási együttható.
A lineáris hőtágulási együttható csak egy adott irányba néztük a tágulást. Valójában természetesen minden irányban történik tágulás, így szügség van egy térfogati hőtágulási együtthatóra, amely a térfogat növekedésének arányát mutatja meg: Mi a kapcsolat alfa és béta között? Nézzük meg!
B04. A hőáramlási tényező fogalma.
A hőáramlási tényezőben minden olyan változót foglaluk össze, ami a hőáramlást befolyásolhatja (pl felület alakja, orientációja, közeg sőrősége, viszkozitása, hővezetőképessége, fajhője, hőtágulási együtthatója)
B05. A Stefan-Boltzmann törvény.
B06. A Kelvin skála és a "hármasponti hőmérséklet".
A Kelvin skála az abszolút hőmérsékleti skála. Sokkal természetesebb megközelítés, mint a Celsius. Miután matematikailag bizonyításra került, hogy kb. -273,15 Celsius foknál hidegebb nem lehet semmi, kézen fekvő volt egy olyan skála bevezetése, amin a 0 fok az abszolút nulla, azaz ami alá ténylegesen nem mehet a hőmérséklet. Azért a Celsius skála beosztását megtartották, egész egyszerűen eltolták -273,15 fokkal a nullát.
A hármasponti hőmérséklet pedig az a hőmérséklet, amelyiken a három halmazállapot egyensúlyban van. Pl a víz hármaspontja 610,1 Pa nyomáson 0,01 C fok.
Hivatalosan a Kelvin skála egy beosztása a víz hármaspontjának az 1/273,16od része, ami gyakorlatilag a Celsius skála beosztása :)
XX. Fejezet
A01. Az ideális gáz állapotegyenlete.
pV = nRT pV = NkT
A02. A molnyi mennyiség definíciója.
db részecske.
Ezt a számot Avogadro-számnak nevezzük.
Egy mól: Bármely anyagból az a mennyiség, ami ugyanannyi elemi részecskét tartalmaz, mint ahány atom található 0,012 kg 12-es C izotrópban.
A03. Az ideális gáz kinetikus modellje.
- A gáz nagyszámú azonos tömegpontból áll
- A részecskék különböző sebességű, véletlen szerű mozgást végeznek, tökéletesen rugalmasan ütköznek egymással és a fallal
- Az ütközések során semmilyen más erő nem hat, csak ütközés kölcsönhatásából származó, valamint az ütközés elhanyagolható ideig tart
A04. Az átlagos kinetikus energia és a hőmérséklet (egyatomos) ideális gáz estén.
A05. A Maxwell-féle sebességeloszlás "diagramja".
http://en.wikipedia.org/wiki/Image:MaxwellBoltzmann-en.svg
B01. Cseppfolyósítható gázok p(V) diagramja és a kritikus pont fogalma.
http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/fig6VaporDomePV_web.jpg
Kritikus pont: A kritikus pont felett nem lehet különbséget tenni a folyadék és a gőz állapot között, mivel e pontban a gőz sűrűsége eléri a vele egyensúlyban lévő folyadékfázis sűrűségét.
B02. A p(T) fázisdiagram és a hármaspont fogalma.
Ahol a három szín találkozik az a hármas pont :) http://www.rfcafe.com/references/general/images/p-t_rfcafe.gif
B03. Az ideális gáz állapotegyenletének a levezetése a kinetikus modell alapján.
B04. A "négyzetes középhőmérséklet" fogalma.
B05. A "legvalószínűbb sebesség" fogalma és értéke "T" hőmérsékletű ideális gáz esetén..
B06. A parciális nyomás fogalma.
A parciális nyomás egy résznyomás, amit akkor fejtene ki a gázelegy adott B komponense, ha az egyedül töltené ki a rendelkezésre álló teljes térfogatot. A B komponens részesedése a rendszer össznyomásából. A komponensek parciális nyomásának összege adja a rendszer össznyomását (Dalton-törvény).
B07. A Maxwell-féle sebességeloszlás matematikai alakja (Tk: 20C-43 feladat)
XXI. Fejezet
!!A01. A termodinamikai rendszer fogalma és a termodinamika nulladik főtétele.
A termodinamikai rendszer az anyagi valóság egy, általunk kiválasztott szempont vagy szempontrendszer szerint elhatárolt része. Az elhatárolás történhet egy valóságos fallal vagy egy látszólagos, képzelt elhatároló felülettel.
Szigetelt rendszer idővel mindig eléri a termikus egyensúlyi állapotot, amely magától sohasem változik meg. Ezt az alapvető tapasztalati törvényt szokták a termodinamika nulladik főtételének is nevezni.
Két rendszer mindegyike termikus egyensúlyban van egy harmadikkal akkor a két rendszer egymással is termikus egyensúlyban van.
!!A02. A belső energia fogalma és a termodinamika első főtétele.
belső energia:
atomok és molekulák véletlenszerű mozgásának energiája
A TERMODINAMIKA ELSŐ FŐTÉTELE
[A belső energia megváltozása] = [A rendszerrel közölt hő] + [A rendszer által a környezeten végzett munka]
Q pozitív, ha hőt közlünk a rendszerrel
W pozitív, ha a rendszer égez munkát a köznyezeten
ΔU pozitív, ha a belső energia növekszik (ΔEb = Uv-Uk, Uv>Uk)
!!A03. Reverzibilis és irreverzibilis folyamatok fogalma.
visszafordítható, visszafordíthatatlan
Reverzibilis folyamatok vagy megfordítható folyamatok lefolytatása után a rendszerrel a folyamatot ellenkező irányba hajtva végre, visszaáll az eredeti állapot , azaz sem a rendszerben sem a környezetben nem jöttek létre az eredeti állapothoz képest változások.
Irreverzibilisnek vagy meg nem fordíthatónak nevezünk egy olyan folyamatot , melynek lefolytatása után a rendszert eredeti állapotába nem tudjuk úgy visszavinni , hogy a rendszerben vagy környezetében ne jöjjön létre az eredeti állapothoz képest változás
!!A04. Az ideális gáz moláris hőkapacitása ("molhő").
!!A05. Az adiabatikus állapotváltozás fogalma.
Q = 0
!!A06. Egyatomos ideális gáz átlagos energiája.
3/2 NkT
!!B01. Az izochor állapotváltozás és () számítása ideális gáz esetén.
V = áll -> W = 0,
!!B02. Az izobár állapotváltozás és () számítása ideális gáz esetén.
p = áll -> W = p,
(Rober Mayer egyenlet)
!!B03. Az izoterm állapotváltozás és () számítása ideális gáz esetén.
T = áll -> pV = áll; -->
!!B04. Ideális gáz adiabatikus állapotváltozása és ábrázolása (p,V) diagrammon..
http://sciaga.onet.pl/_i/Fizykasciaga/adiabata_izoterma.jpg
!!B05. Az adiabatikus állapotváltozás és () számítása ideális gáz esetén.
Q = 0;
!!B06. A (termodinamikai) szabadságfok fogalma.
Az energiatárolás független lehetőségeinek a számát.
!!B07. Az ekvipartíció tétele.
Egyensúly esetén minden termodinamikai szabadságfokra azonos energia jut, részecskénként.
!!B08. A hidrogén CV (moláris hőkapacitásának) változása a hőmérséklet függvényében (rajz és magyarázat).
Hudson-Nelson 523.oldal
!!B09. A Dulong-Petit szabály.
XXII. Fejezet
!!A01. A termodinamika második főtételének Kelvin-Planck féle megfogalmazása.
Lehetetlen olyan periódikusan működő gépet készíteni, ami 100%os hatásfokkal alakít át termikus energiát munkává
!!A02. A termodinamika második főtételének Clausius-féle megfogalmazása.
Lehetetlen olyan periodikusan működőgépet készíteni, ami termikus energiát a hideg testről forró testre visz át anélkül, hogy a környezet munkát végezne rajta.
vagy: a Hő spontán csak a melegebről megy a hideg felé.
!!A03. A Carnot körfolyamat és ábrázolása (p,V) diagrammon.
http://www.grc.nasa.gov/WWW/K-12/airplane/Images/carnot.gif
!!A04. A hőerőgép hatásfoka
Q2 a betáplált hőmérséklet, Q1 pedig amit működése során kényszerszerűen lead
!!A05. A Carnot körfolyamat hatásfoka
A könyvben meghatározott elv szerint T2>T1
!!A06. A termodinamika harmadik főtétel és az abszolút zérus hőmérséklet.
Lehetetlen egy test hőmérsékletét véges számú lépésben ábszolót zérusra csökkenteni.
!!B01. A hűtőgép és a "teljesítménytényezője".
Carnot körfolyamat megfordítva
A könyvben meghatározott elv szerint T2>T1
!!B02. A hőszivattyú és a "teljesítménytényezője".
Carnot körfolyamat megfordítva
A könyvben meghatározott elv szerint T2>T1
!!B03. Az Otto-körfolyamat definíciója és ábrázolása (p,V) diagrammon.
[[1]] http://www.qrg.northwestern.edu/thermo/design-library/otto/Otto-Pv-diagram.gif
!!B04. A Diesel-körfolyamat definíciója és ábrázolása (p,V) diagrammon.
[[2]] http://www.qrg.northwestern.edu/thermo/design-library/diesel/Diesel-Pv-diagram.gif
!!B05. A Stirling-körfolyamat definíciója és ábrázolása (p,V) diagrammon.
[[3]] Itt adiabaták helyett izotermák vannak! http://www.globalcooling.com/images/pvdiag.jpg
!!B06. A Carnot-féle (hatásfok)tétel.
A Carnot körfolyamat a legjobb hatásfokot biztosítja minden olyan lehetséges hőerőgép közül, amely két megadott hőmérséklet között működik.
!!B07. Az abszolút hőmérsékleti skála.
ld. XIX B06.
XXIII. Fejezet
!!A01. Az entropia definíciója (a Carnot körfolyamat alapján).
Az entrópia a rendszer átalakító képességének a mértéke. Azaz adott hőmérséklet eléréséhez mekkora hőt kell betáplálni. Az alábbi megállapítások mind csak reverzibilis folyamatokra érvényesek!!
!!A02. Az entropia mint állapotfüggvény.
Az entrópia csak a rendszer állapotától függ, így alkalmas a rendszer állapotának jellemzésére -> állapotfv.
!!B01. Az entropia megváltozása (ideális gáz) "szabad tágulása" esetén.
!!B02. Az entropia megváltozása fázisátalakulás (pl. jég olvadása) során.
A hőmérséklet állandó marad az egész folyamat során: T = 0°C = 273K.
A hőátvitel a jég-víz fázisátmenetnek köszönhető. A folyamat reverzibilis.
(A jég olvadáshője: )
!!B03 Az entropia változása "kalorimetriás" folyamat esetén (pl.: forró vasat hideg vízbe mártunk).
Hudson-Nelson 551. oldal 23-2 példa
Egy tömegű fajhőjű hőmérsékletű, forró követ tömegű, fajhőjű hőmérsékletű hideg vízbe dobunk .
A végső hőmérséklet .
A folyamat irreverzibilis, mivel véges hőmérsékletkülönbséggel jár. Ha azonban elképzelünk egy kezdeti és végállapotot összekötő reverzibilis folyamatot, az enrópiaváltozás az általunk keresett érték lesz ( mivel az entrópiaváltozás nem függ az úttól ).
A differenciális hőmennyiség:
Az első kifejezés pozitív, mert , a második pedig negatív.
, ezért a pozitív tag nagysága mindig nagyobb, ami mindig entrópianövekedést eredményez.
!!B04. Az enropia változása egyszerű hővezetés esetén.
Hudson-Nelson 551.oldal 23-3 példa
!!B05. A termodinamikai valószínűség.
W = V1/V2
!!B06. Az entropia mikroszkópikus definíciója (a Boltzmann formula).
S = klnW
!!B07. A termodinamika második főtétele és az entropia.
Minden természetes (irrevezibilis) folyamatra:
Csak reverzibilis folyamatokra:
!!B08. Az entropia és az információ kapcsolata.
Az információ (I) alapvető definíciója:
W annak a valószínűsége, hogy bizonyos üzenetet kitalálunk, mielőtt megkapjuk.
Az információ megfelel a negatív entrópiának.
!!B09. Az "örökmozgók".
Az örökmozgó (perpetuum mobile) olyan hipotetikus gép, amit, ha egyszer beindítunk, örökké mozgásban marad, miközben nem von el energiát a környezetétől és a belső energiája is állandó szinten marad. A termodinamika kétféle örökmozgót különböztet meg
- az elsőfajú örökmozgó olyan gép, ami több munkát végez, mint amennyi energiát fölvesz a környezetétől. Egy ilyen gép hatásfoka nagyobb, mint 100%. Az energiamegmaradás törvénye (a termodinamika első főtétele) alapján ilyen gépet nem lehet készíteni.
- a másodfajú örökmozgó olyan gép, ami a környezetéből felvett hőenergiát veszteségek nélkül munkavégzésre tudja fordítani. Egy ilyen gép hatásfoka pontosan 100%. A termodinamika második főtétele alapján ilyen gépet nem lehet készíteni. Egy ilyen gép például az óceánok hőenergiáját tudná hasznosítani.
A villamosságtan első fejezeteihez tartozó ellenőrző kérdések és válaszok a Fizika 2 tárgynál találhatóak! -- MAKond - 2011.01.15.
-- SzelPeter - 2008.05.28.-tól 2008.06.04-ig II.-tól a XXIII. témakörig kb.
-- Silivrian - 2008.06.01.
-- MAKond - 2010.06.12.