„Adatbázisok/ZH feladatok” változatai közötti eltérés
aNincs szerkesztési összefoglaló |
Nincs szerkesztési összefoglaló |
||
| 3. sor: | 3. sor: | ||
TODO. | TODO. | ||
}} | }} | ||
-->Ezen az oldalon néhány feladatot találsz témakörönként az új (VITMAB04) [[Adatbázisok|Adatbázisokhoz]], amik a régi tárgy 1996-2007 közötti ZH feladatsoraiból lettek kiválogatva. Ehhez hasonló jellegű feladatok lehetnek az új tárgyban is. | -->Ezen az oldalon néhány feladatot találsz témakörönként az új (VITMAB04) [[Adatbázisok|Adatbázisokhoz]], amik a régi tárgy 1996-2007 közötti ZH feladatsoraiból lettek kiválogatva. Ehhez hasonló jellegű feladatok lehetnek az új tárgyban is. Az eredeti feladatlapokat megtalálod a [[Adatbázisok_(régi)#Zh|régi tárgy]] oldalán. | ||
== ER modell és diagram, átalakítás relációs sémára == | == ER modell és diagram, átalakítás relációs sémára == | ||
(1996-04-16 1.) Az alábbi leírást egy laikus adta: Egy | (1996-04-16 1.) Az alábbi leírást egy laikus adta: Egy páciensnek számos betegsége is lehet, vannak betegségek, amiben pillanatnyilag senki sem szenved. Minden pácienst egyetlen mentőállomáson kezelnek, akár több orvos is. Az orvosoknak több páciensük is lehet, akik különböző mentőállomásokon is fekhetnek. Egy mentőállomás lehet akár üres is és mindig pontosan egy kórházhoz tartozik. Egy kórháznak esetleg több mentőállomása és több orvosa is van. Egy orvost legfeljebb 3 kórház alkalmaz. A kórházat mindig egy olyan igazgató vezeti, aki a kórház orvosa is, közgazdászdiplomával is rendelkezik és más kórházzal nincs munkaviszonya. | ||
a) Készítsen a fentiekről egyed-kapcsolati diagramot! Tüntesse fel pontosan a kapcsolatok funkcionalitását is! Azonosítsa az egyedeket | a) Készítsen a fentiekről egyed-kapcsolati diagramot! Tüntesse fel pontosan a kapcsolatok funkcionalitását is! Azonosítsa az egyedeket célszerűen megválasztott attribútumokkal, határozza meg a kulcsokat! | ||
b) Alakítsa át a diagramot relációs sémákká úgy, hogy a kapcsolatok megvalósításához a lehető legkevesebb relációt használja! | b) Alakítsa át a diagramot relációs sémákká úgy, hogy a kapcsolatok megvalósításához a lehető legkevesebb relációt használja! | ||
| 41. sor: | 41. sor: | ||
(2002-11-15/B 5. módosítva) Tervezzen ER-diagramot egy színházi adatbázishoz, melyben az alábbiakat akarjuk tárolni. A színházakról nyilvántartjuk a nevüket, címüket, milyen darabokat játszanak jelenleg, kik a dolgozói főállásban. Egy színdarabról tároljuk a címét, szerzőjét, rendezőjét, azt, hogy melyik színházban játsszák és hogy kik szerepelnek benne. A dolgozókról tároljuk nevüket, személyi számukat és hogy melyik színházban dolgoznak. A színészekről ezeken kívül még azt is akarjuk tudni, hogy tudnak-e énekelni és hogy melyik darabokban játszanak, a rendezőkről pedig azt, hogy miket rendeznek. Az alábbi megkötések érvényesek: egy darabot csak egy ember rendez, egy darab csak egy színházban megy, továbbá egy dolgozó csak egy színháznál lehet főállásban. | (2002-11-15/B 5. módosítva) Tervezzen ER-diagramot egy színházi adatbázishoz, melyben az alábbiakat akarjuk tárolni. A színházakról nyilvántartjuk a nevüket, címüket, milyen darabokat játszanak jelenleg, kik a dolgozói főállásban. Egy színdarabról tároljuk a címét, szerzőjét, rendezőjét, azt, hogy melyik színházban játsszák és hogy kik szerepelnek benne. A dolgozókról tároljuk nevüket, személyi számukat és hogy melyik színházban dolgoznak. A színészekről ezeken kívül még azt is akarjuk tudni, hogy tudnak-e énekelni és hogy melyik darabokban játszanak, a rendezőkről pedig azt, hogy miket rendeznek. Az alábbi megkötések érvényesek: egy darabot csak egy ember rendez, egy darab csak egy színházban megy, továbbá egy dolgozó csak egy színháznál lehet főállásban. | ||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
[[Fájl:Adatb zh 2002-11-15-B feladat-5 ER-diagram.png|600px]] | |||
}} | |||
| 62. sor: | 66. sor: | ||
(2007-04-25 1.) Egy óvoda adatait szeretnénk tárolni egy adatbázisban. Az óvodában gyerekek vannak illetve óvónénik és óvóbácsik dolgoznak. Mindenkiről nyilván akarjuk tartani a nevét, személyi számát, születési dátumát és helyét. A gyerekekről tárolni akarjuk az óvodai jelüket és a szüleik mobilszámát, a dolgozókról pedig a diplomázásuk évét. Az óvodában csoportok is vannak, minden csoportnak van neve. Tárolni akarjuk, hogy melyik gyerek melyik csoportba jár és melyik csoportnak ki az óvónénije illetve óvóbácsija. (Egy gyerek egy csoportba jár, egy csoportnak két gondozója van, minden dolgozó pontosan egy csoportban dolgozik.) Az óvodában különórákat is szerveznek, itt tárolni akarjuk a különóra nevét (pl. angol), a különóra időpontját, azt, hogy ki tartja (ez valaki az óvoda dolgozói közül) és hogy kik járnak rá. Készítsen E/K | (2007-04-25 1.) Egy óvoda adatait szeretnénk tárolni egy adatbázisban. Az óvodában gyerekek vannak illetve óvónénik és óvóbácsik dolgoznak. Mindenkiről nyilván akarjuk tartani a nevét, személyi számát, születési dátumát és helyét. A gyerekekről tárolni akarjuk az óvodai jelüket és a szüleik mobilszámát, a dolgozókról pedig a diplomázásuk évét. Az óvodában csoportok is vannak, minden csoportnak van neve. Tárolni akarjuk, hogy melyik gyerek melyik csoportba jár és melyik csoportnak ki az óvónénije illetve óvóbácsija. (Egy gyerek egy csoportba jár, egy csoportnak két gondozója van, minden dolgozó pontosan egy csoportban dolgozik.) Az óvodában különórákat is szerveznek, itt tárolni akarjuk a különóra nevét (pl. angol), a különóra időpontját, azt, hogy ki tartja (ez valaki az óvoda dolgozói közül) és hogy kik járnak rá. Készítsen E/K diagramot ehhez az adatbázishoz, ne feledkezzen el a kulcsok jelöléséről sem. Röviden írja le, hogyan határozta meg az egyes kapcsolatok jellegét. | ||
| 68. sor: | 72. sor: | ||
(2005-04-19 1.) Egy menza havi menüit szeretnénk tárolni | (2005-04-19 1.) Egy menza havi menüit szeretnénk tárolni egy adatbázisban. A menü minden nap egy levest, egy főételt és egy édességet tartalmaz. Egy étel többször is előfordulhat az adott hónapban, de tudjuk, hogy egy adott leves-főétel kombinációhoz, csak egyféle édesség illik. Minden ételnek szeretnénk tárolni a nevét, az energiatartalmát és hogy melyik hozzávalóból mennyi kell. Készíts E/K diagramot az adatbázishoz! | ||
| 84. sor: | 88. sor: | ||
(2006-11-20 1.) Egy középiskola tanárait és diákjait szeretnénk tárolni egy adatbázisban. Mindenkiről nyilván akarjuk tartani a nevét, személyi számát, születési dátumát és helyét. Minden diákról tárolni akarjuk, hogy melyik osztályba jár most (pl. 10.b) és hogy eddig hány évfolyamon bukott. Minden tanárról tároljuk a gúnynevét és azt hogy mely osztályokban mely tárgyakat tanítja, akik pedig osztályfőnökök is, azokról azt is, hogy hol osztályfőnökök és hogy ez hányadik osztályuk a pályafutásuk során. (Minden tanár legfeljebb egy osztályban osztályfőnök egy időben és egy osztálynak csak egy osztályfőnöke van.) | (2006-11-20 1.) Egy középiskola tanárait és diákjait szeretnénk tárolni egy adatbázisban. Mindenkiről nyilván akarjuk tartani a nevét, személyi számát, születési dátumát és helyét. Minden diákról tárolni akarjuk, hogy melyik osztályba jár most (pl. 10.b) és hogy eddig hány évfolyamon bukott. Minden tanárról tároljuk a gúnynevét és azt hogy mely osztályokban mely tárgyakat tanítja, akik pedig osztályfőnökök is, azokról azt is, hogy hol osztályfőnökök és hogy ez hányadik osztályuk a pályafutásuk során. (Minden tanár legfeljebb egy osztályban osztályfőnök egy időben és egy osztálynak csak egy osztályfőnöke van.) | ||
a) Készítsen E/K | a) Készítsen E/K diagrmot ehhez az adatbázishoz, ne feledkezzen el a kulcsok jelöléséről sem. Röviden írja le, hogyan határozta meg az egyes kapcsolatok jellegét. | ||
b) Alakítsa át a az előző pontban adott E/K | b) Alakítsa át a az előző pontban adott E/K diagramot relációs sémává, az órán tanult eljárást használva. | ||
| 109. sor: | 113. sor: | ||
b) azon személyek összességét, akik minden sört kedvelnek azokban a sörözőkben, ahol látogatnak. | b) azon személyek összességét, akik minden sört kedvelnek azokban a sörözőkben, ahol látogatnak. | ||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
a) π<sub>sör</sub>(Kapható) \ π<sub>sör</sub>(π<sub>személy,sör</sub>(Kapható ⋈ Látogat) \ Kedvel) | |||
Magyarázat: π<sub>személy,sör</sub>(Kapható ⋈ Látogat) megadja azt, hogy az emberek milyen sörökhöz juthatnak hozzá, π<sub>személy,sör</sub>(Kapható ⋈ Látogat) \ Kedvel a "rossz" (személy, sör) párokat adja meg, azaz azokat az embereket és söröket, amely emberek megkaphatják kocsmájukban az adott sört, de nem szeretik. Ezen reláció sör-vetülete a "rossz" sörök halmaza, ezt kell kivonni az összes sör halmazából. Itt hallgatólagosan feltettük, hogy minden sör kapható valahol. Megjegyzés: Az olyan relációs algabrai kifejezések, melyekben csak , , , , vetítés és szelekció fordul elő, szükségképpen monotonok, abban az értelemben, hogy ha a kifejezésekben szereplő alaprelációkat bővítjük, akkor az eredmény semmiképpen sem lesz szűkebb. Ez a monotonitás azonban nem igaz a feladatbeli relációra: például ha a Kapható relációt bővítjük egy olyan (Kocsma, Sör) párral, amely sörnek egy esküdt ellensége látogatja az adott kocsmát, akkor ezzel a "jó" sörök halmaza szűkül(het). Ezért biztosan nem jók azok a megoldások, melyekben csak a fenti műveletek szerepelnek. | |||
b) π<sub>személy</sub>(Látogat) \ π<sub>személy</sub>(π<sub>személy,sör</sub>(Kapható ⋈ Látogat) \ Kedvel) | |||
}} | |||
| 130. sor: | 142. sor: | ||
b) megkeresi azon a dolgozók nevét, akik Catherine Janeway kapitány hajóján dolgoznak. | b) megkeresi azon a dolgozók nevét, akik Catherine Janeway kapitány hajóján dolgoznak. | ||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
a) π<sub>dolgozónév</sub>(π<sub>azonosító,dolgozónév</sub>(Dolgozó) ⋈ (π<sub>hajónév,azonosító</sub>(Beosztás) ⋈ π<sub>hajónév</sub>(σ<sub>faj='klingon'</sub>(Csillaghajó))) | |||
b) CJHajói = π<sub>hajónév</sub>(σ<sub>rang='kapitány'</sub>(π<sub>azonosító</sub>(σ<sub>dolgozónév='Catherine Janeway'</sub>(Dolgozó)) ⋈ Beosztás)) | |||
π<sub>dolgozónév</sub>(Dolgozó ⋈ π<sub>azonosító</sub>(Beosztás ⋈ CJHajói)) | |||
}} | |||
---- | ---- | ||
(2002-11-15/A-B 4.) Legyen R és S két, azonos attribútumokkal rendelkező reláció, X pedig ezen közös attribútumhalmaz egy részhalmaza. Mely igaz (melyek igazak) az alábbi állítások közül? | (2002-11-15/A-B 4.) Legyen R és S két, azonos attribútumokkal rendelkező reláció, X pedig ezen közös attribútumhalmaz egy részhalmaza. Mely igaz (melyek igazak) az alábbi állítások közül? Válaszodat indokold! | ||
a) π<sub>X</sub>(R ∩ S) = π<sub>X</sub>(R) ∩ π<sub>X</sub>(S) | a) π<sub>X</sub>(R ∩ S) = π<sub>X</sub>(R) ∩ π<sub>X</sub>(S) | ||
| 141. sor: | 160. sor: | ||
c) π<sub>X</sub>(R \ S) = π<sub>X</sub>(R) \ π<sub>X</sub>(S) | c) π<sub>X</sub>(R \ S) = π<sub>X</sub>(R) \ π<sub>X</sub>(S) | ||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
a) Nem igaz. Ellenpélda: legyen a két séma R(A, B) és S(A, B), X legyen az A-ból álló egy elemű halmaz. R-nek csak egy sora legyen: (a,b), és S-nek is csak egy sora legyen: (a,b'). Ekkor π<sub>A</sub>(R ∩ S) = ∅, de π<sub>A</sub>(R) ∩ π<sub>A</sub>(S) = {a}. | |||
b) Igaz. Mindkét irányba megmutatjuk a tartalmazást. Először belátjuk, hogy π<sub>X</sub>(R ∪ S) ⊆ π<sub>X</sub>(R) ∪ π<sub>X</sub>(S) igaz. Ha egy t sor eleme π<sub>X</sub>(R ∪ S)-nak, akkor létezik olyan t' sor R ∪ S-ben definíció szerint, hogy t'-nek X-re eső vetülete éppen t. Az unió definíciója miatt t' ∈ R vagy t' ∈ S fennáll. Mivel t a t' X-re eső vetülete, ezért vagy t ∈ π<sub>X</sub>(R) vagy t ∈ π<sub>X</sub>(S) igaz lesz és így t ∈ π<sub>X</sub>(R) ∪ π<sub>X</sub>(S). | |||
A másik irányban: Ha t ∈ π<sub>X</sub>(R) ∪ π<sub>X</sub>(S), akkor t ∈ π<sub>X</sub>(R) vagy t ∈ π<sub>X</sub>(S) fennáll, tegyük fel, hogy t ∈ π<sub>X</sub>(R) (a másik eset hasonló). Ekkor létezik definíció szerint egy olyan t' ∈ R sor, melynek X-re eső vetülete éppen t. De mivel t' ∈ R ∪ S is igaz, ezért t ∈ π<sub>X</sub>(R ∪ S) is fennáll. | |||
c) Nem igaz. Ellenpélda: legyen a két séma R(A, B) és S(A, B), X legyen az A-ból álló egy elemű halmaz. R-nek csak egy sora legyen: (a,b), és S-nek is csak egy sora legyen: (a,b'). Ekkor π<sub>A</sub>(R \ S) = {a}, de π<sub>A</sub>(R) \ π<sub>A</sub>(S) = ∅. | |||
}} | |||
| 181. sor: | 210. sor: | ||
(2000-11-17/A-B 4.) Legyenek R(A, B, C, D) és S(C, D, E) alaprelációk, és | (2000-11-17/A-B 4.) Legyenek R(A, B, C, D) és S(C, D, E) alaprelációk, és legyen | ||
a) π<sub>AC</sub>(σ<sub>E=2</sub>(R ⋈ S)) | |||
b) π<sub>CD</sub>(R) ∩ π<sub>CD</sub>(S) | |||
belőle képzett leszármaztatott reláció. Fejezze ki ez utóbbit sor- és oszlopkalkulussal. | |||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
a) | |||
Sorkalkulussal: { t<sup>(2)</sup> | ∃u<sup>(4)</sup> ∃v<sup>(3)</sup> R(u) ∧ S(v) ∧ u[3] = v[1] ∧ u[4] = v[2] ∧ v[3] = '2' ∧ t[1] = u[1] ∧ t[2] = u[3] } | |||
Oszlopkalkulussal: { a, c | ∃b ∃d ∃e R(a,b,c,d) ∧ S(c,d,e) ∧ e = '2' } | |||
b) | |||
Sorkalkulussal: { t<sup>(2)</sup> | ∃u<sup>(4)</sup> ∃v<sup>(3)</sup> R(u) ∧ S(v) ∧ u[3] = v[1] ∧ u[4] = v[2] ∧ t[1] = u[3] ∧ t[2] = u[4] } | |||
Oszlopkalkulussal: { c, d | ∃a ∃b ∃e R(a,b,c,d) ∧ S(c,d,e) } | |||
}} | |||
| 187. sor: | 236. sor: | ||
(2002-11-15/A 3.a) Az R | (2002-11-15/A 3.a) Az R reláció attribútumai (A; B; C; D; E) az S reláció attribútumai pedig (A; B; F; G). Fejezze ki sorkalkulus segítségével R ⋈ S-et! | ||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
{ t<sup>(7)</sup> | ∃r<sup>(5)</sup> ∃s<sup>(4)</sup> ( R(r) ∧ S(s) ∧ r[1] = s[1] ∧ r[2] = s[2] ∧ r[1] = t[1] ∧ r[2] = t[2] ∧ r[3] = t[3] ∧ r[4] = t[4] ∧ r[5] = t[5] ∧ s[3] = t[6] ∧ s[4] = t[7] ) } | |||
}} | |||
| 193. sor: | 246. sor: | ||
(2002-11-15/A 3.b) Az R | (2002-11-15/A 3.b) Az R reláció attribútumai (A; B ; C; D), az S-é pedig (C; D). Ekkor R ÷ S, R és S hányadosa, azon (A; B) attribútumú t sorokból áll, melyekre igaz, hogy bármely S-beli s sor esetén a ts sor R-ben van. Fejezze ki R ÷ S-t oszlopkalkulus segítségével! Feltehetjük, hogy az S reláció nem üres. | ||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
{a, b | ∀c ∀d ( R(a, b, c, d) ∨ ¬S(c, d) ) } | |||
Magyarázat: Egy (a,b) pár pontosan akkor van benne a hányadosban, ha minden S-beli (c,d) párra (a,b,c,d) R-ben van. Azaz annak kell teljesülnie, hogy S(c, d) implikálja R(a, b, c, d)-t minden (c,d) esetén. Az S(c, d) → R(a, b, c, d) implikációt pedig R(a, b, c, d) ∨ ¬S(c, d) alakba lehet írni. | |||
}} | |||
| 230. sor: | 289. sor: | ||
d) A kulcs R-ben, B kulcs S-ben? | d) A kulcs R-ben, B kulcs S-ben? | ||
(Ez tehát 8 különböző kérdés, mindegyik eredményt | (Ez tehát 8 különböző kérdés, mindegyik eredményt indokold röviden.) | ||
| 284. sor: | 343. sor: | ||
b) 2-szintes ritka index | b) 2-szintes ritka index | ||
segítségével szeretnénk tárolni. Adjon értelmes alsó becslést az összes | segítségével szeretnénk tárolni. Adjon értelmes alsó becslést az összes szükséges blokk számára az alábbi feltételek mellett: az állomány 3 millió rekordból áll, egy rekord hossza 300 byte, egy blokk mérete 1000 byte, a kulcshossz 45 byte, egy mutató hossza 5 byte. | ||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
a) A főállományban 3 × 10<sup>6</sup> rekord van, és mivel rekordok nem lóghatnak át blokkhatáron, ezért ehhez kell 10<sup>6</sup> blokk. A sűrű indexben annyi bejegyzés lesz, mint ahány rekord van a főállományban, azaz 3 × 10<sup>6</sup>. Egy blokkra pontosan 20 bejegyzés fér: ez 1,5 × 10<sup>5</sup> blokk. Ez azt is jelenti, hogy a ritka indexben lesz legalább 1,5 × 10<sup>5</sup> bejegyzés, ehhez kell még 7,5 × 10<sup>5</sup> blokk. Ez összesen 1157500 blokk. | |||
b) A főállományban 3 × 10<sup>6</sup> rekord van, és mivel rekordok nem lóghatnak át blokkhatáron, ezért ehhez kell legalább 10<sup>6</sup> blokk. Az első ritka indeben lesz ennyi bejegyzés, azaz 10<sup>6</sup>. Egy blokkra pontosan 20 bejegyzés fér: ez legalább 5 × 10<sup>4</sup> blokk. Ez azt is jelenti, hogy a második szintű ritka indexben lesz 5 × 10<sup>4</sup> bejegyzés, ehhez kell még 25 × 10<sup>2</sup> blokk. Ez összesen 1052500 blokk. | |||
}} | |||
| 301. sor: | 366. sor: | ||
(2002-11-15/A 1. módosítva) Egy 240000 rekordból álló állományt szeretnénk tárolni. Két lehetőség közül választhatunk: vagy sűrű indexre épített 1-szintes ritka indexet használunk, vagy 3-szintes ritka indexet. Melyik megoldást lehet kevesebb blokk felhasználásával megvalósítani, ha még azt is el szeretnénk érni, hogy sem az indexállományban, sem a főállományban ne legyenek 80%-nál telítettebb blokkok? Tudjuk, hogy egy blokk mérete 1500 byte, egy rekord hossza 350 byte, a kulcs hossza 45 byte, a mutató hossza pedig 15 byte. | (2002-11-15/A 1. módosítva) Egy 240000 rekordból álló állományt szeretnénk tárolni. Két lehetőség közül választhatunk: vagy sűrű indexre épített 1-szintes ritka indexet használunk, vagy 3-szintes ritka indexet. Melyik megoldást lehet kevesebb blokk felhasználásával megvalósítani, ha még azt is el szeretnénk érni, hogy sem az indexállományban, sem a főállományban ne legyenek 80%-nál telítettebb blokkok? Tudjuk, hogy egy blokk mérete 1500 byte, egy rekord hossza 350 byte, a kulcs hossza 45 byte, a mutató hossza pedig 15 byte. | ||
{{Rejtett|mutatott='''Megoldás'''|szöveg= | |||
A sűrű indexes verziónál: A főállomány 80.000 blokkból fog állni, mert egy blokkra 3 rekord fér csak rá (1500 × 80% = 1200 byte hasznos hely van egy blokkon és egy rekord 350 byte). Egy blokk 20 darab kulcs+mutató pár fér el, mert az 1200 byte a hasznos hely laponként és egy pár helyigénye 60 byte. Így a sűrű indexhez kell 12.000 blokk (mert van 240.000 indexbejegyzés, annyi, amennyi rekord van a főállományban). A ritka indexhez pedig kell 600 blokk, mivel 12.000 indexbejegyzést kell elhelyeznünk (ennyi blokk van a sűrű indexben). Ez összesen 92.600 blokk (főállomány, sűrű index, ritka index) | |||
A másik verzió esetén: A főállomány itt is 80.000 blokk lesz és egy blokkra most is 20 indexbejegyzés fér el. A fentiek miatt, az első szintű ritka indexben lesz 4.000 blokk (mert 80.000 indexbejegyzésnek kell hely), a második szinten lesz 200 blokk, a harmadikon pedig 10. Azaz összesen lesz 84.210 blokk, ami kevesebb, mint az előbb, azaz ez a takarékosabb megoldás. | |||
}} | |||
A lap 2018. december 27., 00:14-kori változata
Ezen az oldalon néhány feladatot találsz témakörönként az új (VITMAB04) Adatbázisokhoz, amik a régi tárgy 1996-2007 közötti ZH feladatsoraiból lettek kiválogatva. Ehhez hasonló jellegű feladatok lehetnek az új tárgyban is. Az eredeti feladatlapokat megtalálod a régi tárgy oldalán.
ER modell és diagram, átalakítás relációs sémára
(1996-04-16 1.) Az alábbi leírást egy laikus adta: Egy páciensnek számos betegsége is lehet, vannak betegségek, amiben pillanatnyilag senki sem szenved. Minden pácienst egyetlen mentőállomáson kezelnek, akár több orvos is. Az orvosoknak több páciensük is lehet, akik különböző mentőállomásokon is fekhetnek. Egy mentőállomás lehet akár üres is és mindig pontosan egy kórházhoz tartozik. Egy kórháznak esetleg több mentőállomása és több orvosa is van. Egy orvost legfeljebb 3 kórház alkalmaz. A kórházat mindig egy olyan igazgató vezeti, aki a kórház orvosa is, közgazdászdiplomával is rendelkezik és más kórházzal nincs munkaviszonya.
a) Készítsen a fentiekről egyed-kapcsolati diagramot! Tüntesse fel pontosan a kapcsolatok funkcionalitását is! Azonosítsa az egyedeket célszerűen megválasztott attribútumokkal, határozza meg a kulcsokat!
b) Alakítsa át a diagramot relációs sémákká úgy, hogy a kapcsolatok megvalósításához a lehető legkevesebb relációt használja!
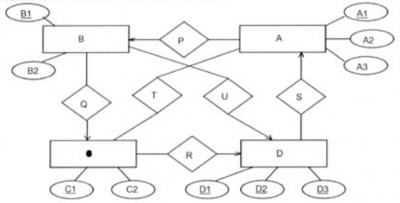
(2000-04-25 1. módosítva) Alakítsa át az alábbi ER diagramot relációs sémára úgy, hogy minimális számú sémát használjon fel!
(2000-11-17/A 1. módosítva) Alakítson ki ER-modellt, ami személyeket, munkahelyeiket és munkáikat leíró (egyszerűsített) adatbázis alapjául szolgálhat. Az alábbiakat szeretnénk ábrázolni. Személy; név, személyi szám, lakcím, munkahely(ek), beosztás(ok), projektek, amiken dolgozik. Eszköz; megnevezés, azonosító, tulajdonos cég, a projekt(ek) amiben használják. Cég; név, cím, vezető, dolgozók, projektek. Projekt; elnevezés, vezető, érintett cég(ek), határidő, résztvevők.
(2001-11-16 1.) Adott az alábbi E-R diagram, amely egy videokölcsönző üzlet működéséhez szükséges elemeket tartalmazza: a kazettákat, ügyfeleket, kölcsönzéseket, előjegyzéseket.
Alakítsa át a diagramot relációs sémákba úgy, hogy a lehető legkevesebb relációs sémát definiálja! A relációs séma elemeit a megfelelő ER-diagrambeli elemmel azonosan nevezze el.
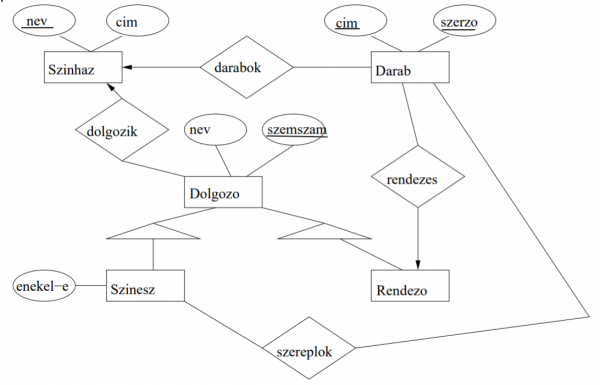
(2002-11-15/B 5. módosítva) Tervezzen ER-diagramot egy színházi adatbázishoz, melyben az alábbiakat akarjuk tárolni. A színházakról nyilvántartjuk a nevüket, címüket, milyen darabokat játszanak jelenleg, kik a dolgozói főállásban. Egy színdarabról tároljuk a címét, szerzőjét, rendezőjét, azt, hogy melyik színházban játsszák és hogy kik szerepelnek benne. A dolgozókról tároljuk nevüket, személyi számukat és hogy melyik színházban dolgoznak. A színészekről ezeken kívül még azt is akarjuk tudni, hogy tudnak-e énekelni és hogy melyik darabokban játszanak, a rendezőkről pedig azt, hogy miket rendeznek. Az alábbi megkötések érvényesek: egy darabot csak egy ember rendez, egy darab csak egy színházban megy, továbbá egy dolgozó csak egy színháznál lehet főállásban.
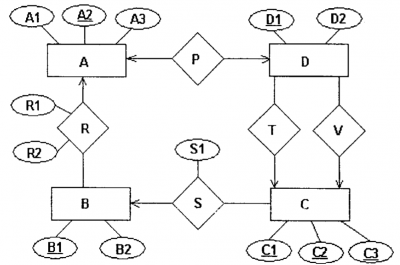
(2004-06-02 4. módosítva) Alakítsa át az alábbi ER diagramot relációs sémára!
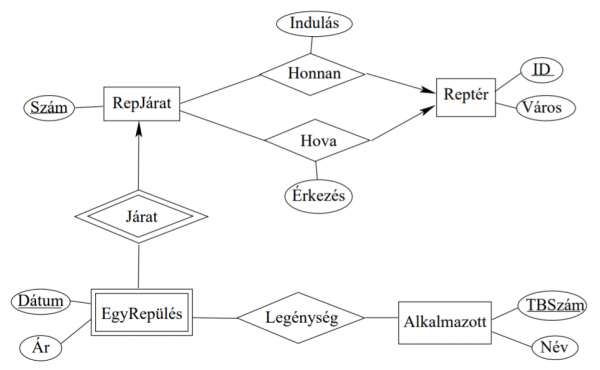
(2004-11-19 1.) A következő egyed kapcsolat modell egy repülőtársaság adatbázisának egyszerűsített tervét tartalmazza. A következő információkat szeretnénk tárolni: Repülőtér; az azonosító kódját és a várost ahol van, RepJárat; különböző járatok számát, az indulási és érkezési időpontot és repteret (minden járat leszállás nélkül közlekedik), EgyRepülés; egy adott járat konkrét napon való közlekedését és az aznapra beosztott legénységet (de nincs feltüntetve ki milyen beosztásban van, pl. ki a pilóta, ... ), Alkalmazott: az összes alkalmazott TBSzáma és neve. Alakíts ki egy megfelelő relációs sémát a modellhez! Törekedj a redundancia-mentességre! Ne felejtsd el megadni a kulcsokat!
(2007-04-25 1.) Egy óvoda adatait szeretnénk tárolni egy adatbázisban. Az óvodában gyerekek vannak illetve óvónénik és óvóbácsik dolgoznak. Mindenkiről nyilván akarjuk tartani a nevét, személyi számát, születési dátumát és helyét. A gyerekekről tárolni akarjuk az óvodai jelüket és a szüleik mobilszámát, a dolgozókról pedig a diplomázásuk évét. Az óvodában csoportok is vannak, minden csoportnak van neve. Tárolni akarjuk, hogy melyik gyerek melyik csoportba jár és melyik csoportnak ki az óvónénije illetve óvóbácsija. (Egy gyerek egy csoportba jár, egy csoportnak két gondozója van, minden dolgozó pontosan egy csoportban dolgozik.) Az óvodában különórákat is szerveznek, itt tárolni akarjuk a különóra nevét (pl. angol), a különóra időpontját, azt, hogy ki tartja (ez valaki az óvoda dolgozói közül) és hogy kik járnak rá. Készítsen E/K diagramot ehhez az adatbázishoz, ne feledkezzen el a kulcsok jelöléséről sem. Röviden írja le, hogyan határozta meg az egyes kapcsolatok jellegét.
(2005-04-19 1.) Egy menza havi menüit szeretnénk tárolni egy adatbázisban. A menü minden nap egy levest, egy főételt és egy édességet tartalmaz. Egy étel többször is előfordulhat az adott hónapban, de tudjuk, hogy egy adott leves-főétel kombinációhoz, csak egyféle édesség illik. Minden ételnek szeretnénk tárolni a nevét, az energiatartalmát és hogy melyik hozzávalóból mennyi kell. Készíts E/K diagramot az adatbázishoz!
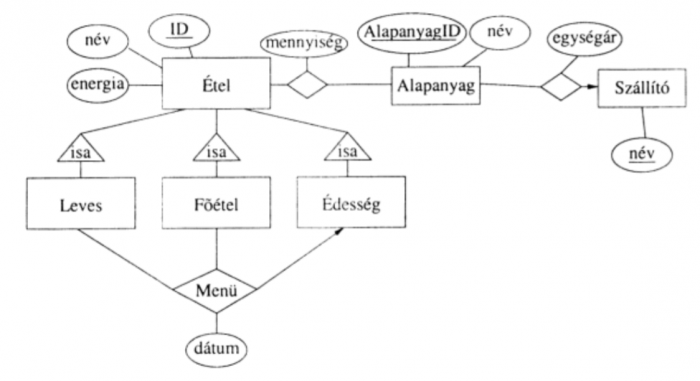
(2005-05-03 1. módosítva) A következő E/K modellhez határozz meg relációs sémát!
(2006-11-20 1.) Egy középiskola tanárait és diákjait szeretnénk tárolni egy adatbázisban. Mindenkiről nyilván akarjuk tartani a nevét, személyi számát, születési dátumát és helyét. Minden diákról tárolni akarjuk, hogy melyik osztályba jár most (pl. 10.b) és hogy eddig hány évfolyamon bukott. Minden tanárról tároljuk a gúnynevét és azt hogy mely osztályokban mely tárgyakat tanítja, akik pedig osztályfőnökök is, azokról azt is, hogy hol osztályfőnökök és hogy ez hányadik osztályuk a pályafutásuk során. (Minden tanár legfeljebb egy osztályban osztályfőnök egy időben és egy osztálynak csak egy osztályfőnöke van.)
a) Készítsen E/K diagrmot ehhez az adatbázishoz, ne feledkezzen el a kulcsok jelöléséről sem. Röviden írja le, hogyan határozta meg az egyes kapcsolatok jellegét.
b) Alakítsa át a az előző pontban adott E/K diagramot relációs sémává, az órán tanult eljárást használva.
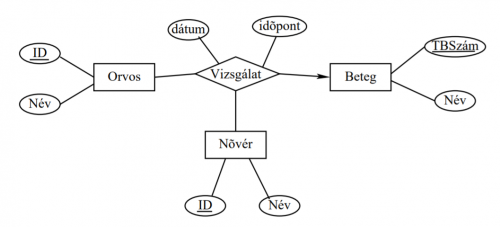
(2004-11-30 1. módosítva) A következő egyed kapcsolat modell egy orvosi rendelő adatbázisának egyszerűsített tervét tartalmazza. Alakíts ki egy megfelelő relációs séma tervet ugyanehhez az adatbázishoz! Törekedj a redundanciamentességre! Ne felejtsd el megadni a kulcsokat!
Relációs adatmodell
(2004-06-02 2.) Ha egy A attribútum kardinalitása kisebb, mint az A domén elemeinek száma, akkor A nem lehet (egyszerű) kulcs. Igazolja vagy cáfolja az állítást!
Relációs algebra
(2000-11-17/A-B 3.) Tekintsük a következő alaprelációkat (a kézenfekvő értelmezéssel): Kedvel(személy, sör), Kapható(söröző,sör), Látogat(személy, söröző). Fejezze ki relációs algebra segítségével
a) azon sörök összességét, melyeket minden látogató kedvel azokban a sörözőkben, ahol kaphatók.
b) azon személyek összességét, akik minden sört kedvelnek azokban a sörözőkben, ahol látogatnak.
a) πsör(Kapható) \ πsör(πszemély,sör(Kapható ⋈ Látogat) \ Kedvel)
Magyarázat: πszemély,sör(Kapható ⋈ Látogat) megadja azt, hogy az emberek milyen sörökhöz juthatnak hozzá, πszemély,sör(Kapható ⋈ Látogat) \ Kedvel a "rossz" (személy, sör) párokat adja meg, azaz azokat az embereket és söröket, amely emberek megkaphatják kocsmájukban az adott sört, de nem szeretik. Ezen reláció sör-vetülete a "rossz" sörök halmaza, ezt kell kivonni az összes sör halmazából. Itt hallgatólagosan feltettük, hogy minden sör kapható valahol. Megjegyzés: Az olyan relációs algabrai kifejezések, melyekben csak , , , , vetítés és szelekció fordul elő, szükségképpen monotonok, abban az értelemben, hogy ha a kifejezésekben szereplő alaprelációkat bővítjük, akkor az eredmény semmiképpen sem lesz szűkebb. Ez a monotonitás azonban nem igaz a feladatbeli relációra: például ha a Kapható relációt bővítjük egy olyan (Kocsma, Sör) párral, amely sörnek egy esküdt ellensége látogatja az adott kocsmát, akkor ezzel a "jó" sörök halmaza szűkül(het). Ezért biztosan nem jók azok a megoldások, melyekben csak a fenti műveletek szerepelnek.
b) πszemély(Látogat) \ πszemély(πszemély,sör(Kapható ⋈ Látogat) \ Kedvel)
(2001-11-16 2.) Egy könyvtári kölcsönzéseket segítő relációs adatbázis négy relációjának a sémái az alábbiak. Az azonos nevű attribútumok jelentése is azonos. KÖNYV(RAKT, SZERZO, CIM), KÖLCS(RAKT, O_ID, K_DATUM), OLVASO(O_ID, O_NEV, LAKCIM), VISSZA(RAKT, O_ID, V_DATUM, K_ID) A relációk, ill. attribútumaik jelentése rendre a könyvtári KÖNYVek RAKTári száma (egyedi azonosító), SZERZŐje és CÍMe, a KÖLCSönzött könyvek RAKTári száma, a kölcsönző Olvasó egyedi azonosítója és a Kölcsönzés DÁTUMa. Az OLVASÓ reláció az Olvasók azonosítóját, NEVét és LAKCÍMét tartalmazza. Amikor egy könyvet VISSZAhoznak, akkor belekerül a vissza relációba, a V_DATUM értéke pedig a visszavétel dátuma lesz, K_ID a visszavevő könyvtáros azonosítója.
a) Adjon meg egy relációalgebrai kifejezést, amely azt a relációt állítja elő, amely azoknak az olvasóknak a neveit valamint az általuk kölcsönzött könyvek szerzőit és címeit tartalmazza, amelyeket az olvasók 2001. okt. folyamán késve hoztak vissza a könyvtárba. A kölcsönzési idő 1 hónap.
b) Mit tudunk mondani a jelenleg kölcsönzés alatt lévő könyvekről?
(2002-11-15/A 2. módosított) Tekintsük az alábbi Csillagflotta adatbázissémát: Csillaghajó(hajónév, év, faj), Dolgozó(dolgozónév, azonosító, születés), Beosztás(azonosító, hajónév, rang). A relációk jelentése: Csillaghajó; a hajó neve, gyártási éve és az, hogy melyik faj tervei alapján készült, Dolgozó; neve, Csillagflotta-azonosítója, mikor született, Beosztás: melyik dolgozó, melyik hajón, milyen rangban dolgozik. Adjunk relációs algebrai kifejezést, mely
a) előállítja azon a dolgozók nevét, akik klingon (faj által tervezett) hajón dolgoznak.
b) megkeresi azon a dolgozók nevét, akik Catherine Janeway kapitány hajóján dolgoznak.
a) πdolgozónév(πazonosító,dolgozónév(Dolgozó) ⋈ (πhajónév,azonosító(Beosztás) ⋈ πhajónév(σfaj='klingon'(Csillaghajó)))
b) CJHajói = πhajónév(σrang='kapitány'(πazonosító(σdolgozónév='Catherine Janeway'(Dolgozó)) ⋈ Beosztás))
πdolgozónév(Dolgozó ⋈ πazonosító(Beosztás ⋈ CJHajói))
(2002-11-15/A-B 4.) Legyen R és S két, azonos attribútumokkal rendelkező reláció, X pedig ezen közös attribútumhalmaz egy részhalmaza. Mely igaz (melyek igazak) az alábbi állítások közül? Válaszodat indokold!
a) πX(R ∩ S) = πX(R) ∩ πX(S)
b) πX(R ∪ S) = πX(R) ∪ πX(S)
c) πX(R \ S) = πX(R) \ πX(S)
a) Nem igaz. Ellenpélda: legyen a két séma R(A, B) és S(A, B), X legyen az A-ból álló egy elemű halmaz. R-nek csak egy sora legyen: (a,b), és S-nek is csak egy sora legyen: (a,b'). Ekkor πA(R ∩ S) = ∅, de πA(R) ∩ πA(S) = {a}.
b) Igaz. Mindkét irányba megmutatjuk a tartalmazást. Először belátjuk, hogy πX(R ∪ S) ⊆ πX(R) ∪ πX(S) igaz. Ha egy t sor eleme πX(R ∪ S)-nak, akkor létezik olyan t' sor R ∪ S-ben definíció szerint, hogy t'-nek X-re eső vetülete éppen t. Az unió definíciója miatt t' ∈ R vagy t' ∈ S fennáll. Mivel t a t' X-re eső vetülete, ezért vagy t ∈ πX(R) vagy t ∈ πX(S) igaz lesz és így t ∈ πX(R) ∪ πX(S).
A másik irányban: Ha t ∈ πX(R) ∪ πX(S), akkor t ∈ πX(R) vagy t ∈ πX(S) fennáll, tegyük fel, hogy t ∈ πX(R) (a másik eset hasonló). Ekkor létezik definíció szerint egy olyan t' ∈ R sor, melynek X-re eső vetülete éppen t. De mivel t' ∈ R ∪ S is igaz, ezért t ∈ πX(R ∪ S) is fennáll.
c) Nem igaz. Ellenpélda: legyen a két séma R(A, B) és S(A, B), X legyen az A-ból álló egy elemű halmaz. R-nek csak egy sora legyen: (a,b), és S-nek is csak egy sora legyen: (a,b'). Ekkor πA(R \ S) = {a}, de πA(R) \ πA(S) = ∅.
(2007-04-25 2.) Tekintsük a következő három relációból álló adatbázissémát (ami a Húsvéti Nyúl számára készült): Gyerek(GyerekNév, Nem, SzületésiÉv) (milyen nevű, milyen nemű gyerek mikor született), Kér(GyerekNév, JátékNév) (melyik gyerek mit kért húsvétra), Kap(GyerekNév, JátékNév) (melyik gyerek mit kap húsvétra). Adja meg relációs algebrával azon gyerekek nevét, akik semmi olyat nem kapnak, amit kértek. (Azt feltehetjük, hogy minden gyerek kért legalább egy dolgot.)
(2006-11-20 2.) Tekintsük a következő két relációból álló adatbázissémát: Hallgató (HallgatóNév, Nem, Neptunkód) (milyen nevű, milyen nemű hallgatónak mi a Neptun kódja, kulcs a Neptunkód), Átlagok(Neptunkód, Félév, Átlag) (melyik Neptun kódhoz milyen átlag tartozik egy adott félévben, kulcs a (Neptunkód, Félév) pár). Adja meg relációs algebrával azon hallgatók nevét, akik a "2006/2007/1" félévben a legmagasabb átlagot érték el.
(2004-11-30 3.a) Tekintsük az alábbi adatbázissémát: Járat(Járatszám, Honnan, Hova, Távolság, Indul, Érkezik), Repülőtípus(TípusAzonosító, TípusNév, Hatótávolság), Jogosítvány(PilótaAzonosító, TípusAzonosító), Pilóta(PilótaAzonosító, PilótaNév). A relációk jelentése: Járat; melyik számú járat mikor és honnan, mikor és hova érkezik, mennyi távolságot tesz meg (kulcs a Járatszám), Repülőtípus; a típus azonosítója, neve és mennyit tud megtenni leszállás nélkül (kulcs a TípusAzonosító), Jogosítvány; milyen azonosítójú pilóta milyen azonosítójú gépet tud elvezetni (itt a PilótaAzonosító és a TípusAzonosító együtt alkot kulcsot), Pilóta; milyen azonosítójú polóta és mi a neve (kulcs a PilótaAzonosító). Fejezd ki relációs algebrával azon repülőgépek TípusAzonosítóit, melyek leszállás nélkül el tudnak repülni Budapestről Bombayba.
Sor- és oszlopkalkulus
(1996-04-16 5.) Adott az alábbi relációs adatbázis: LÁTOGAT(KORHELY, KOCSMA), ÁRUL(KOCSMA, SÖR), KEDVEL(KORHELY, SÖR). A relációk értelme rendre: azon KOCSMÁk, amiket egy KORHELY látogat; melyik KOCSMA milyen SÖRt árul; a KORHELYek melyik SÖRöket kedvelik.
Adjon meg egy sorkalkulus kifejezést arra a relációra, amely azokat a korhelyeket tartalmazza, akik látogatnak olyan kocsmát, amely árul olyan sört, amelyet a korhely kedvel!
(2000-04-25 3.) Adott az alábbi relációs adatbázis: GYÁRT(CÉG, TÍPUS, ÁR), SZERETI(VEVŐ, TIPLIS), DOLGOZIK(VEVŐ, CÉG, BEOSZTÁS) A relációk jelentése rendre: azon autóTÍPUSok, amiket egy CÉG gyárt az azok eladási ÁRa; egy VEVŐ melyik autóTÍPUSt szereti; a VEVŐ melyik CÉGnél dolgozik, milyen BEOSZTÁSban.
a) Adjon meg egy sorkalkulus kifejezést, amely azokat a vevőket tartalmazó relációt állítja elő, akik olyan cégnél dolgoznak, amelyek gyártanak olyan autótípust, amilyet a vevő szeret!
b.) Vizsgálja meg, hogy a felírt kifejezés biztonságos-e!
(2000-11-17/A-B 4.) Legyenek R(A, B, C, D) és S(C, D, E) alaprelációk, és legyen
a) πAC(σE=2(R ⋈ S))
b) πCD(R) ∩ πCD(S)
belőle képzett leszármaztatott reláció. Fejezze ki ez utóbbit sor- és oszlopkalkulussal.
a)
Sorkalkulussal: { t(2) | ∃u(4) ∃v(3) R(u) ∧ S(v) ∧ u[3] = v[1] ∧ u[4] = v[2] ∧ v[3] = '2' ∧ t[1] = u[1] ∧ t[2] = u[3] }
Oszlopkalkulussal: { a, c | ∃b ∃d ∃e R(a,b,c,d) ∧ S(c,d,e) ∧ e = '2' }
b)
Sorkalkulussal: { t(2) | ∃u(4) ∃v(3) R(u) ∧ S(v) ∧ u[3] = v[1] ∧ u[4] = v[2] ∧ t[1] = u[3] ∧ t[2] = u[4] }
Oszlopkalkulussal: { c, d | ∃a ∃b ∃e R(a,b,c,d) ∧ S(c,d,e) }
(2002-11-15/A 3.a) Az R reláció attribútumai (A; B; C; D; E) az S reláció attribútumai pedig (A; B; F; G). Fejezze ki sorkalkulus segítségével R ⋈ S-et!
(2002-11-15/A 3.b) Az R reláció attribútumai (A; B ; C; D), az S-é pedig (C; D). Ekkor R ÷ S, R és S hányadosa, azon (A; B) attribútumú t sorokból áll, melyekre igaz, hogy bármely S-beli s sor esetén a ts sor R-ben van. Fejezze ki R ÷ S-t oszlopkalkulus segítségével! Feltehetjük, hogy az S reláció nem üres.
{a, b | ∀c ∀d ( R(a, b, c, d) ∨ ¬S(c, d) ) }
Magyarázat: Egy (a,b) pár pontosan akkor van benne a hányadosban, ha minden S-beli (c,d) párra (a,b,c,d) R-ben van. Azaz annak kell teljesülnie, hogy S(c, d) implikálja R(a, b, c, d)-t minden (c,d) esetén. Az S(c, d) → R(a, b, c, d) implikációt pedig R(a, b, c, d) ∨ ¬S(c, d) alakba lehet írni.
(2004-06-02 5.) Vizsgálja meg, hogy biztonságos-e a sorkalkulus. Minden változó doménje a természetes számok halmaza, alma1 = {2,3}.
{ x(1) | (∃ t(1)) x(1)[1] = t(1)[1] ∧ t(1)[1] > 2 ∧ alma(1)(x(1)) }
(2007-04-25 3.) Tekintsük a következő három relációból álló adatbázissémát (ami a Húsvéti Nyúl számára készült): Gyerek(GyerekNév, Nem, SzületésiÉv) (milyen nevű, milyen nemű gyerek mikor született), Kér(GyerekNév, JátékNév) (melyik gyerek mit kért húsvétra), Kap(GyerekNév, JátékNév) (melyik gyerek mit kap húsvétra).
a) Fogalmazza meg szavakkal, hogy mit fejez ki az alábbi sorkalkulusos kifejezés: { t(1) | (∃ u(3)) (u[1] = t[1] ∧ Gyerek(u) ∧ (∀ v(2)) ( v[1] ≠ t[1] ∨ ¬Kér(v) ∨ Kap(v) ) ) }
b) Biztonságos-e a fenti kifejezés?
c) Megadható-e relációs algebrával az a) pontban adott halmaz?
(2005-04-19 2.) Adott egy r és egy s reláció, melyek rendre az R(A, B) illetve az S(B, C) sémára illeszkednek. r-nek nr csupa különböző sora van, s-nek pedig ns. Legfeljebb és legalább hány sora lehet (nr és ns függvényében) az r ⋈ s relációnak, ha
a) A kulcs R-ben,
b) B kulcs R-ben,
c) B kulcs R-ben és S-ben is,
d) A kulcs R-ben, B kulcs S-ben?
(Ez tehát 8 különböző kérdés, mindegyik eredményt indokold röviden.)
(2005-05-03 2.) Adott a következő séma: Jegyek(Neptun, DiákNév, Tárgykód, Jegy). (Melyik diák melyik tárgyból milyen jegyet kapott, kulcs a. (Neptun, Tárgykód) pár.) Fejezd ki sorkalkulussal azokat a tárgykódokat, amely tárgyakból csak olyan diákok szereztek jegyet, akik Legalább egy tárgyból szereztek legalább elégségest.
(2006-11-20 3.) Adott a következő séma: Jegyek (Neptun, DiákNév, Tárgykód, Jegy). (Melyik diák melyik tárgyból milyen jegyet kapott, kulcs a (Neptun, Tárgykód) pár.)
a) Biztonságos-e az alábbi sorkalkulusos kifejezés? {s(1) | ∃ q(4)(Jegyek(q) ∧ q[3] = s[1]) ∧ ∀t(4)(¬Jegyek(t) ∨ s[1] ≠ t[3] ∨ t[4] = '5') }
b) Fejezze ki szavakkal, hogy mit ír le a fenti sorkalkulusos kifejezés.
(2004-11-30 3.b) Tekintsük az alábbi adatbázissémát: Járat(Járatszám, Honnan, Hova, Távolság, Indul, Érkezik), Repülőtípus(TípusAzonosító, TípusNév, Hatótávolság), Jogosítvány(PilótaAzonosító, TípusAzonosító), Pilóta(PilótaAzonosító, PilótaNév). A relációk jelentése: Járat; melyik számú járat mikor és honnan, mikor és hova érkezik, mennyi távolságot tesz meg (kulcs a Járatszám), Repülőtípus; a típus azonosítója, neve és mennyit tud megtenni leszállás nélkül (kulcs a TípusAzonosító), Jogosítvány; milyen azonosítójú pilóta milyen azonosítójú gépet tud elvezetni (itt a PilótaAzonosító és a TípusAzonosító együtt alkot kulcsot), Pilóta; milyen azonosítójú polóta és mi a neve (kulcs a PilótaAzonosító). Fejezd ki sorkalkulussal azon repülőgépek TípusAzonosítóit, melyek leszállás nélkül el tudnak repülni Budapestről Bombayba.
Fizikai adatbázis
(1996-04-16 3.) Egy 15525 rekordból álló állományt szeretnénk ritka index szervezéssel tárolni. A rekordhossz 850 byte, egy blokk kapacitása (a fejrészt nem számítva) 4000 byte. A kulcs 50 byte-os, egy mutatóhoz 18 byte kell.
a) Legalább hány blokkra van szükség?
b) Mennyi ideig tart legfeljebb egy rekord tartalmának kiolvasása, ha az operatív tárban rendelkezésünkre álló szabad hely 5000 byte? Segít-e a legnagyobb rekordhozzáférési idő csökkentésében, ha 10-szer (100-szor) ennyi szabad memóriával gazdálkodhatunk?
(2000-04-25 2.) Létrehozunk egy állományt, amelyben "vödrös hash" szervezéssel tároljuk a rekordokat 2048 vödörben. A rekordhossz 260 byte, egy blokk kapacitása (a fejrészt nem számítva) 1500 byte. A kulcsok 40 byte-osak, egy mutatóhoz 9 byte kell. Egy blokkművelet feltételezett időigénye 10 ms. A vödörkatalógust kereséskor a memóriában tároljuk.
a) Mekkora az a maximális rekordmennyiség, amely mellett tetszőlegesen kiválasztott kedvező feltételeke esetén nem több, mint 30 ms alatt megtalálunk az állományban?
b) Legfeljebb hány blokkot foglal el ilyenkor a teljes struktúra (vödörkatagólussal együtt) a diszken?
c) Hogyan lehet a rekordelérési idő maximumát a lehető legkevesebb többlet-memóriával a 2/3-ára csökkenteni, és mennyi memória kell ehhez?
(2000-11-17/A-B 2. módosítva) Egy állományt
a) sűrű index, majd erre épített 1-szintes ritka index
b) 2-szintes ritka index
segítségével szeretnénk tárolni. Adjon értelmes alsó becslést az összes szükséges blokk számára az alábbi feltételek mellett: az állomány 3 millió rekordból áll, egy rekord hossza 300 byte, egy blokk mérete 1000 byte, a kulcshossz 45 byte, egy mutató hossza 5 byte.
a) A főállományban 3 × 106 rekord van, és mivel rekordok nem lóghatnak át blokkhatáron, ezért ehhez kell 106 blokk. A sűrű indexben annyi bejegyzés lesz, mint ahány rekord van a főállományban, azaz 3 × 106. Egy blokkra pontosan 20 bejegyzés fér: ez 1,5 × 105 blokk. Ez azt is jelenti, hogy a ritka indexben lesz legalább 1,5 × 105 bejegyzés, ehhez kell még 7,5 × 105 blokk. Ez összesen 1157500 blokk.
b) A főállományban 3 × 106 rekord van, és mivel rekordok nem lóghatnak át blokkhatáron, ezért ehhez kell legalább 106 blokk. Az első ritka indeben lesz ennyi bejegyzés, azaz 106. Egy blokkra pontosan 20 bejegyzés fér: ez legalább 5 × 104 blokk. Ez azt is jelenti, hogy a második szintű ritka indexben lesz 5 × 104 bejegyzés, ehhez kell még 25 × 102 blokk. Ez összesen 1052500 blokk.
(2001-11-16 3.) Egy nagy távközlési cég a hívásrekordjait adatbázisban tárolja. A max. 1 milliárd darab 200 byte-os rekordot tartalmazó állomány rekordjait szeretnénk minél hatékonyabban elérni annak figyelembe vételével, hogy benne a kereséseket két különböző kulcs szerint is 35 msec-on belül végre kell tudni hajtani. A blokkméret 8000 byte, a blokkelérési idő 4 msec, mindkét kulcs hossza 10 byte, a mutatók 32 bitesek. Az adatállomány blokkjai a háttértáron rendezetlenül helyezkednek el. Az egyszerűség kedvéért tételezzük fel, hogy a memóriában egyszerre csak egyetlen blokk tárolására van lehetőség. A megoldásnak támogatnia kell az intervallumkeresést is.
a) Javasoljon megoldást a problémára a tantárgyban tanult módszerek közül és bizonyítsa is be, hogy a javaslata valóban kielégíti a specifikációt! Készítsen magyarázó ábrát is a megoldásjavaslatához!
b) Egy alkalommal meg is kell valósítani az intervallumkeresést az egyik kulcs alapján. A találati halmaz várhatóan a rekordoknak mintegy 9%-át fogja tartalmazni. Adjon javaslatot a lekérdezés végrehajtására, hogy az a lehető legrövidebb időn belül lefusson!
(2002-11-15/A 1. módosítva) Egy 240000 rekordból álló állományt szeretnénk tárolni. Két lehetőség közül választhatunk: vagy sűrű indexre épített 1-szintes ritka indexet használunk, vagy 3-szintes ritka indexet. Melyik megoldást lehet kevesebb blokk felhasználásával megvalósítani, ha még azt is el szeretnénk érni, hogy sem az indexállományban, sem a főállományban ne legyenek 80%-nál telítettebb blokkok? Tudjuk, hogy egy blokk mérete 1500 byte, egy rekord hossza 350 byte, a kulcs hossza 45 byte, a mutató hossza pedig 15 byte.
A sűrű indexes verziónál: A főállomány 80.000 blokkból fog állni, mert egy blokkra 3 rekord fér csak rá (1500 × 80% = 1200 byte hasznos hely van egy blokkon és egy rekord 350 byte). Egy blokk 20 darab kulcs+mutató pár fér el, mert az 1200 byte a hasznos hely laponként és egy pár helyigénye 60 byte. Így a sűrű indexhez kell 12.000 blokk (mert van 240.000 indexbejegyzés, annyi, amennyi rekord van a főállományban). A ritka indexhez pedig kell 600 blokk, mivel 12.000 indexbejegyzést kell elhelyeznünk (ennyi blokk van a sűrű indexben). Ez összesen 92.600 blokk (főállomány, sűrű index, ritka index)
A másik verzió esetén: A főállomány itt is 80.000 blokk lesz és egy blokkra most is 20 indexbejegyzés fér el. A fentiek miatt, az első szintű ritka indexben lesz 4.000 blokk (mert 80.000 indexbejegyzésnek kell hely), a második szinten lesz 200 blokk, a harmadikon pedig 10. Azaz összesen lesz 84.210 blokk, ami kevesebb, mint az előbb, azaz ez a takarékosabb megoldás.
(2004-06-02 3.) Vödrös hash-elést alkalmazunk, rekordok száma 12500000, egy rekord hossza 240 byte, egy blokkba 4000 byte fér el, egy kulcs hossza 25 byte, a mutatóé 8 byte. Mekkora legyen a vödrök minimális száma ha a keresés során maximum 5 blokkelérési idő alatt akarjuk megtálalni a keresett rekordot? (Feltételezhetjük hogy a hash függvény egyenletesen osztja el a kulcsokat, és a keresés során a vödör-katalógust a memóriában tároljuk.) Minimum hány byte-os a hash-tábla?
Optimalizálás
(2004-11-30 4.) Legyen r egy olyan R(A, B, C, D) sémára illeszkedő reláció, melynek 40000 sora van, 20 fér el egy blokkban, és van rá építve ritka index. Ennek keresési kulcsának mérete egy sor hosszának tizede. Az s reláció az S(A, E, F, G) sémára illeszkedik, 25000 sora van, egy blokkba 5 sor fér el. Tudjuk, hogy mindkét relációban az A attribútum értékei teljesen egyenletesen oszlanak el, minden érték pontosan 5-ször fordul elő. A memóriában 401 blokk fér el egyszerre. Legalább hány blokkolvasást kell végeznünk ha az r ⋈ s relációt
a) beágyazott ciklikus algoritmussal
b) az indexet használó algoritmussal
számítjuk ki?