„Makroökonómia jelölések” változatai közötti eltérés
A VIK Wikiből
| 70. sor: | 70. sor: | ||
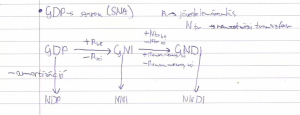
[[Fájl:gdp.png|keretnélküli|GDP-s dolgok]] | [[Fájl:gdp.png|keretnélküli|GDP-s dolgok]] | ||
<math>GDP = Y = Y + I_B + G + (X - I_m); I_B \rightarrow \text{bruttó beruházás}; (X-I_m) \rightarrow \text{belföldi többlet/nettó export}< | <math>GDP = Y = Y + I_B + G + (X - I_m); I_B \rightarrow \text{bruttó beruházás}; (X-I_m) \rightarrow \text{belföldi többlet/nettó export}</math> | ||
<math>NDP = C + I_n + G + (X-I_m)</math> | <math>NDP = C + I_n + G + (X-I_m)</math> | ||
| 82. sor: | 82. sor: | ||
* <math>S_0 = -L_0</math> | * <math>S_0 = -L_0</math> | ||
<math>Y + t_{rv} = W + t_v + S_v</math> | <math>Y + t_{rv} = W + t_v + S_v</math> | ||
* <math>\frac{M}{P} = L^D \rightarrow \text{Lm | * <math>\frac{M}{P} = L^D \rightarrow \text{Lm görbe}</math> | ||
<math>T_{rh} + W = C + t_h + S_h</math> | <math>T_{rh} + W = C + t_h + S_h</math> | ||
* <math>\mathbf{C = C_0 + \hat{C} \cdot Y}</math> | * <math>\mathbf{C = C_0 + \hat{C} \cdot Y}</math> | ||
A lap 2017. november 17., 14:45-kori változata
Itt találhatók a Mikmak for dummies I. elején szereplő rövidítések és képletek olvasható és kereshető formában.
Jelölések
|
Képletek
I. Adótól független II. - ??? - transzfer - Adó
|