„Orvosi képdiagnosztika-ACM Snake” változatai közötti eltérés
A VIK Wikiből
aNincs szerkesztési összefoglaló |
aNincs szerkesztési összefoglaló |
||
| 2. sor: | 2. sor: | ||
== Jegyzetek == | == Jegyzetek == | ||
* [http://home.mit.bme.hu/~hadhazi/Oktatas/OKD/diak/Snake_16.pdf ACM Snake diák ( | * [http://home.mit.bme.hu/~hadhazi/Oktatas/OKD/diak/Snake_16.pdf ACM Snake diák 2016] (nehezen érhető) | ||
* [https://en.wikipedia.org/wiki/Active_contour_model ACM Snake wikipedia] | * [https://en.wikipedia.org/wiki/Active_contour_model ACM Snake wikipedia] (bevezetőnek jó) | ||
* '''[https://pdfs.semanticscholar.org/a4ef/a6a763f808863d7e2ded15a14e3c5d439363.pdf ACM Snake publikáció]''' (a teljes anyagot lefedi, részletes és könnyen érhető) | |||
== Összefoglaló == | == Összefoglaló == | ||
A lap 2016. december 20., 10:11-kori változata
Az Orvosi képdiagnosztika tárgy egyik témaköre.
Jegyzetek
- ACM Snake diák 2016 (nehezen érhető)
- ACM Snake wikipedia (bevezetőnek jó)
- ACM Snake publikáció (a teljes anyagot lefedi, részletes és könnyen érhető)
Összefoglaló
Az ACM (Active Contour Modell) Snake célja egy objektum kontúrjainak meghatározása egy zajos képen.
Ellenőzrő kérdések (2016)
Ismertesse formálisan a Snake futása során megvalósított optimalizálási feladatot az energiapotenciál (E(x)) felhasználásával. Mit tud mondani az optimalizálási probléma algoritmikus nehézségéről? Az energiapotenciál esetén mi az integrandus egyes tagjainak interpretációja? Az belső energia egyes tagjai milyen kényszereket gyakorolnak a szegmentáló görbe pontjaira?
Amennyiben a többi energiatag értéke x-től független skalár, abban az esetben milyen az optimalizáció végén előálló szegmentáló görbe?
[TODO]
Legmeredekebb lejtő módszere esetén a Snake minimalizálandó energiafüggvények a megváltozását az alábbi összefüggés definiálja: . Oldja fel az jelöléseket! Mit tudunk a legmeredekebb lejtő által megválasztott irányáról, és mit a hosszáról? (Segítségül a görbe belső energiáját az alábbi összefüggés definiálja: .)
[TODO]
Mi az Euler-Lagrange optimalizáció / feltétel alapötlete? Mondja ki a feltételt a Snake esetén! Amennyiben a Snake esetén teljesül a feltétel, akkor megtalálta az eljárás a globálisan minimális energiájú görbét? A kérdésre adott válaszát indokolja! Származtassa 1D diszkrét jelek esetén a Laplace szűrés, illetve a 4-edik derivált diszkrét közelítését.
[TODO]
Magyarázza el a szemi-implicit minimalizáció alapötletét, és formálisan ismertesse a szemiimplicit minimalizáció egy-egy iterációját a Snake eljárás esetén (megelégszünk a differenciálegyenlet diszkretizáltjával, nem szükséges a pentadiagonális mátrix felírása). Segítségül a módszerrel Snake esetén az egyenlet megoldását keressük, ahol és definiálja a Snake kontúrját s „helyen”.
[TODO]
Hogyan jelentkezik a lokális optimum probléma a Snake szegmentáló eljárás esetén. Milyen módszereket ismer a probléma kezelésére? Mi az ú.n. kétfázisú szegmentáció lényege (gondoljon az esettanulmányra)? A mellékelt ábrák segítségével magyarázza el az energiafüggvény/energiapotenciál multiscale Gaussal történő elmosásán alapuló többlépéses szegmentálás lényegét: 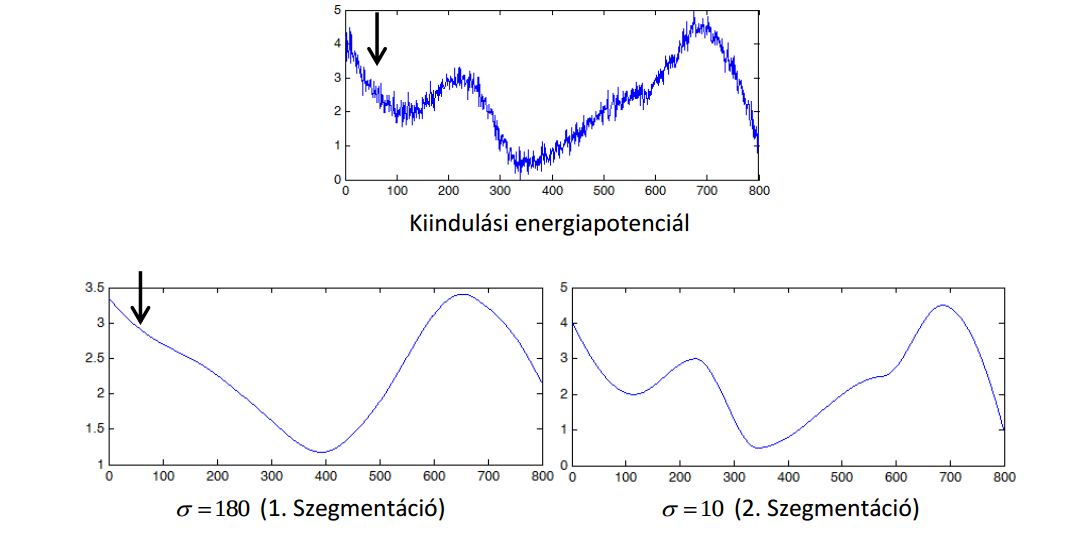

Fekete nyíllal jelöljük a Snake minimalizációjának kiindulási állapotát. Jelölje be, hogy az első szegmentáció leállásának az állapotát, és a 2. Szegmentáció indulásának és leállásának a helyét. Az ábrák és saját ismeretei alapján interpretálja paraméter értének megválasztását.
[TODO]
| 1. félév (tavasz) | |
|---|---|
| 2. félév (ősz) | |
| Egyéb | |
| Szakirányok | |
