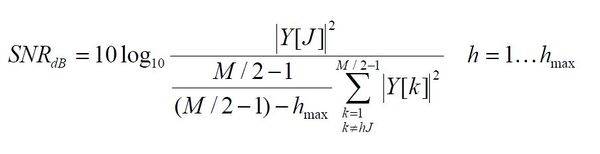„Laboratórium 2 - 7. Mérés ellenőrző kérdései” változatai közötti eltérés
| 116. sor: | 116. sor: | ||
Ha le akarjuk írni a D/A-átalakító transzfer karakterisztikánk a problémánk az, hogy | Ha le akarjuk írni a D/A-átalakító transzfer karakterisztikánk a problémánk az, hogy | ||
összesen 2^N+2 ismeretlent kell meghatároznunk, a nemlinearitási hibák miatt. Ehhez első | összesen <math>2^N+2</math> ismeretlent kell meghatároznunk, a nemlinearitási hibák miatt. | ||
lépésként egy ideális egyenest kell becsléssel meghatároznunk, erre létezik két módszer: | |||
*A végpontokra illesztett egyenes a legegyszerűbb megoldás a fenti problémára. A nemlinearitási hibát a karakterisztika két pontjában nullának definiáljuk: ez a két pont a karakterisztika két szélső értéke, tehát a 0 digitális kódhoz, illetve a végértékhez tartozó szint. Így a modellben máris csak 2^N ismeretlen maradt, így a lineáris egyenletrendszer megoldásával a keresett paraméterek egyszerűen meghatározhatóak. | Ehhez első lépésként egy ideális egyenest kell becsléssel meghatároznunk, erre létezik két módszer: | ||
*A végpontokra illesztett egyenes a legegyszerűbb megoldás a fenti problémára. A nemlinearitási hibát a karakterisztika két pontjában nullának definiáljuk: ez a két pont a karakterisztika két szélső értéke, tehát a 0 digitális kódhoz, illetve a végértékhez tartozó szint. Így a modellben máris csak <math>2^N</math> ismeretlen maradt, így a lineáris egyenletrendszer megoldásával a keresett paraméterek egyszerűen meghatározhatóak. | |||
*A legkisebb négyzetes becslő matematikailag kifinomultabb módszert használ a probléma megoldására. A statikus karakterisztika pontjaira egy egyenest illeszt úgy, hogy az illesztett egyenes és a pontsereg közti négyzetes távolság a lehető legkisebb legyen | *A legkisebb négyzetes becslő matematikailag kifinomultabb módszert használ a probléma megoldására. A statikus karakterisztika pontjaira egy egyenest illeszt úgy, hogy az illesztett egyenes és a pontsereg közti négyzetes távolság a lehető legkisebb legyen | ||
A lap 2014. március 1., 17:53-kori változata
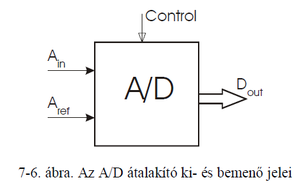
1. Mit jelent az analóg/digitális átalakítás? Milyen bemeneti/kimeneti jelei vannak egy A/D átalakítónak?
Az analóg-digitális átalakító olyan eszköz, amely a bemenetére adott folytonos amplitúdójú, folytonos vagy diszkrét idejű jelet - amely a specifikált teljes kivezérlés tartományba esik - leképezi egy diszkrét amplitúdójú, diszkrét idejű jellé.
Az A/D átalakító ki- és bemenő jelei:
- Egy analóg bemenetet (szimmetrikus, vagy aszimmetrikus, unipoláris vagy bipoláris), amire az analóg bemeneti jel jut.
- Egy referencia bemenetet (ami lehet fizikailag külső, vagy már az IC-re integrált), amellyel a bemeneti jelet összehasonlítja (megfelelő skálázás után).
- Egy digitális vezérlő bemenetet, amellyel az átalakítás paraméterei a külvilág által befolyásolhatóak - átalakítás triggerelése, szóhossz, stb.
- Egy digitális adatkimenetet, ahol az átalakítás végeredménye a külvilág számára hozzáférhető.
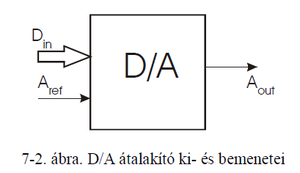
2. Mit jelent a digitális/analóg átalakítás? Milyen bemeneti/kimeneti jelei vannak egy D/A átalakítónak?
A digitális-analóg átalakító a bemeneti digitális szimbólumnak megfelelő analóg kimeneti jelet állítja elő. A kimeneti jel lehet feszültség vagy áram, de legtöbbször az áramkimenetű átalakítók jelét rögtön feszültséggé alakítja egy áram/feszültség-konverter erősítő.
Az D/A átalakító ki- és bemenő jelei:
- Egy analóg kimenetet (feszültség vagy áram).
- Egy analóg referencia bemenetet (ami lehet fizikailag külső, vagy már az IC-re integrált), amellyel a kimeneti jelet skálázza.
- Egy digitális adatbemenetet, ahol az átalakítandó digitális kód megadható.
3. Magyarázza el a szukcesszív-approximációs A/D átalakítás működési elvét [1,2]!
A szukcesszív-approximációs módszer a sorozatos közelítésen alapul. A konvertálandó jelet a komparátor összehasonlítja a DA-átalakító kimenőjelével. Eltérés esetén, az eltérés előjelétől függő irányban, a vezérlő módosítja a regiszter tartalmát, míg a komparátor egyenlőséget nem jelez. Egyensúlyi állapotban a digitális kimeneten megjelenő számérték az analóg bemeneti jelnek felel meg. A legcélszerűbb algoritmus erre a "felezéses" algoritmus. Itt első lépésként az MSB jelenik meg a regiszteren, ha ez túl nagy lefele feleződik az egyel kisebb helyiértékű bittel, ha túl kicsi felfele megy a következő bittel.
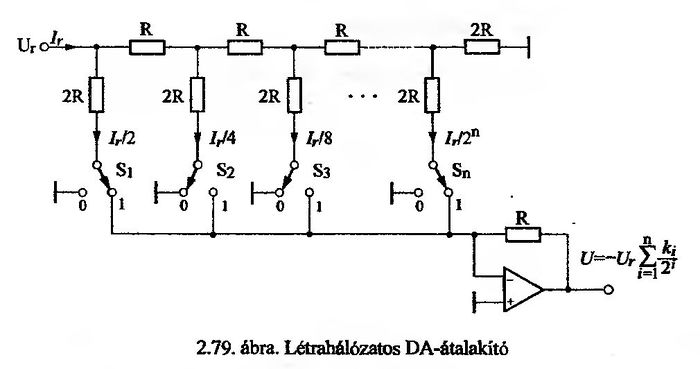
4. Magyarázza el a létrahálózatos D/A átalakítás működési elvét [1,2]!
Sokféle D/A átalakító létezik, az egyik kedvelt típus a létrahálózatos D/A-átalakító. A létrahálózat binárisan súlyozott áramokat szállít a kapcsolóegység részére. A kapcsolók a digitális bemenőjeltől függő pozíciójának megfelelően a binárisan súlyozott áramok lineáris kombinációja jut a műveleti erősítő bemenetére. A műveleti erősítő és visszacsatoló ellenállása, mint áram feszültség átalakító az áramösszegből arányos feszültséget képez a kimeneten. Szükség van még Ur referenciafeszültségre.
5. Rajzolja fel a szinuszos jellel történő A/D átalakító vizsgálat mérési elrendezését!
Aki tudja erre a kérdésre a választ, az NE tartsa magában! ;)
6. Mit jelent a koherens mintavételezés? Hogyan biztosítjuk a periódusonként eltérő fázist?
A/D átalakító vizsgálatának elterjedt módja a hisztogramm teszt, amire gyakran szinuszjelet használnak. A hisztogram teszt lényege, hogy egy ismert sűrűségfüggvényű jelet adunk az átalakító bemenetére. A kimeneti kódok hisztogramját előállítva és összevetve az eredeti jel sűrűségfüggvényével, az átalakító statikus karakterisztikája illetve számos egyéb paramétere meghatározható. Ahhoz, hogy a hisztogram ne torzuljon, a jelből egész számú periódust kell mintavételezni. Ez másképpen azt jelenti, hogy a jel frekvenciája (fi) és a mintavételi frekvencia (fs) közötti fent kell állnia az alábbi egyenlőségnek: fi=J*(fs/M), ahol M a vett minták száma, J pedig a mintavett periódusok száma (J és M egész). Ezt nevezzük koherens mintavételezésnek. De ha a periódusok száma osztója a minták számának, akkor minden egyes periódusnál ugyanabban a fázishelyzetben veszünk mintát, ilyenkor a több periódus nem ad több információt, mint egyetlen egy. Így ahhoz, hogy a kvantálási hiba "kellően zajszerű" legyen, J és M relatív prím kell, hogy legyen.
7. Definiálja az SNR, SINAD, THD fogalmát (az idő és/vagy a frekvenciatartományban)!
A SINAD (SIgnal-to-Noise And Distortion ratio, azaz jel-zaj és torzítás viszony) megadja a jelteljesítmény valamint a zaj és harmonikus komponensek teljesítményének arányát:
Időtartományban:
Frekvenciatartományban:
A SNR (signal-to-noise ratio, azaz jel-zaj viszony) az A/D teszteléshez kapcsolódó fogalmak közül a legkevésbé egyértelmű. Egy lehetséges frekvenciatartománybeli definíció:
Kézi számításoknál élhetünk az alábbi közelítéssel, ahol a zaj átlagértéke dB-ben:
A harmonikus tartalom jellemzésére szolgál a THD (total harmonic distortion, azaz teljes harmonikus torzítás ). Értéke az átalakító transzfer karakterisztikájának nemlinearitásaitól függ. A THD-val a felharmonikusok teljesítményét az alapharmonikus teljesítményéhez viszonyítjuk:
8. Mi a statikus karakterisztika ofszet és erősítés hibája?
Ha az átalakító bemenetére adott digitális kódot a legkisebb és legnagyobb érték (tipikusan 0 és 2^N-1) között változtatjuk, és a kimeneti feszültséget pontról pontra megmérjük, akkor megkapjuk az átalakító statikus karakterisztikáját. A karakterisztikára ideális esetben egy egyenes illeszthető.
Az átalakítóban használt aktív és diszkrét elemek miatt jelentkezik az erősítés és ofszet hiba. Az erősítés hiba miatt az ideálistól eltérő lesz a karakterisztika meredeksége Az ofszet hiba elsősorban az átalakítóban megtalálható aktív elemek ofszetfeszültsége miatt jelentkezik. Ennek következménye, hogy 0 bemeneti kód esetén a kimeneti feszültség nem lesz nulla.
9. Mi a különbség a végpontok közötti és a legkisebb-négyzetes becslés alapján számított lineáris karakterisztika között?
Ha le akarjuk írni a D/A-átalakító transzfer karakterisztikánk a problémánk az, hogy összesen ismeretlent kell meghatároznunk, a nemlinearitási hibák miatt.
Ehhez első lépésként egy ideális egyenest kell becsléssel meghatároznunk, erre létezik két módszer:
- A végpontokra illesztett egyenes a legegyszerűbb megoldás a fenti problémára. A nemlinearitási hibát a karakterisztika két pontjában nullának definiáljuk: ez a két pont a karakterisztika két szélső értéke, tehát a 0 digitális kódhoz, illetve a végértékhez tartozó szint. Így a modellben máris csak ismeretlen maradt, így a lineáris egyenletrendszer megoldásával a keresett paraméterek egyszerűen meghatározhatóak.
- A legkisebb négyzetes becslő matematikailag kifinomultabb módszert használ a probléma megoldására. A statikus karakterisztika pontjaira egy egyenest illeszt úgy, hogy az illesztett egyenes és a pontsereg közti négyzetes távolság a lehető legkisebb legyen
10. Mit nevezünk az A/D átalakító átváltási szintjének?
A kód átváltási szint (code transition level) megadja azt az analóg jelszintet, amikor a digitális kimeneti érték két szomszédos érték között változik.
Egy N-bites átalakítónál számú átváltási szint értelmezhető.
11. Mit jelent az integrális nemlinearitási hiba?
Az átalakító karakterisztikája nemlineáris hibákkal is terhelt. A nemlinearitások jellemzése kétféle módon történhet, az integrális és differenciális nemlinearitási hibával illetve diagrammal. Az átalakító integrális nemlinearitása (INL) egy adott bemeneti kód esetén a valódi és az illesztett egyenes által meghatározott kimeneti feszültség különbségével egyezik meg. Minden egyes bemeneti kombinációhoz tartozik egy INL érték, az adatlapokon azonban szokás az integrális nemlinearitási diagramnak csak a maximumát megadni. LSB-ben szokás kifejezni.
12. Mit jelent a differenciális nemlinearitási hiba?
Az átalakító karakterisztikája nemlineáris hibákkal is terhelt. A nemlinearitások jellemzése kétféle módon történhet, az integrális és differenciális nemlinearitási hibával illetve diagrammal. A differenciális nemlinearitás (DNL) megadja, hogy két szomszédos bemeneti kombinációhoz tartozó kimeneti feszültségérték különbsége mennyivel tér el az illesztett egyenes által meghatározott LSB-től. LSB-ben szokás kifejezni.
13. Mi a kvantálási hiba?
Kvantálásnak nevezzük azt a folyamatot, amikor az analóg jel folytonos értékeit diszkrét értékekké alakítjuk át. Sajnálatos módon a kvantálásnál nem mondható ki a mintavételezésnél megismert rekonstrukciós tételhez hasonló állítás, azaz a kvantált jelből nem állítható vissza pontosan az eredeti jel.
A kvantálási hiba, amely egyébként a bemenet determinisztikus függvénye, sokszor jól modellezhető zajként (különösen nagy bitszámú átalakításkor). Ilyenkor a kimenő kvantált jelet a bemenő analóg jel és a kvantálási zaj összegeként modellezzük.
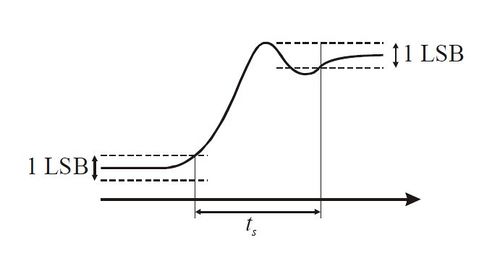
14. Definiálja a D/A átalakító beállási idejét!
A mai korszerű D/A átalakítók többnyire tartalmaznak egy belső buffer regisztert, amely a bemeneti digitális jelet eltárolja és meghajtja az átalakítót magát. A D/A átalakító beállási idejét úgy definiálják, hogy a digitális bemenetben történő változástól a kimeneti jel végső értékétől ±1/2 LSB-re történő beállásáig eltelt idő. Mivel a belső regiszter késleltetését általában nem tudjuk mérni, emiatt elterjedt az önmagában a kimeneti jel alapján definiált beállási idő. Ez a kezdeti értékhez képesti ±1/2 LSB-s hibasáv elhagyása, és a végső értékhez képesti ±1/2 LSB-s hibasávban maradásig eltelt idő. A gyártók legtöbbször egy adatot adnak meg a beállási idő alatt: vagy az úgynevezett végérték beállási időt (full-scale settling time), amely a 0 bemeneti értékből a 2^N-1 értékhez tartozó beállási idő, illetve a középponti beállási időt (midscale settling time), ami a 0111…1 értékből 1000…0 értékbe (vagy 1000…0 értékből 0111…1 értékbe) váltáshoz szükséges idő.
15. Mekkora egy 0.02 V ofszet hibájú és 2.48 V végértékű, 12 bites D/A átalakító LSB-je?
Az ismert összefüggés: