„Laboratórium 2 - 9. Mérés ellenőrző kérdései” változatai közötti eltérés
a →16. |
|||
| 66. sor: | 66. sor: | ||
[[Fájl:Labor2 kép19.jpg]] | [[Fájl:Labor2 kép19.jpg]] | ||
== 16. == | == 16. Rajzolja fel a hurokerősítés törtvonalas Bode-diagramját (<math> \zeta < 0,707 </math>). == | ||
A 15. kérdés ábráján van ennek a kérdésnek a válasza is! | |||
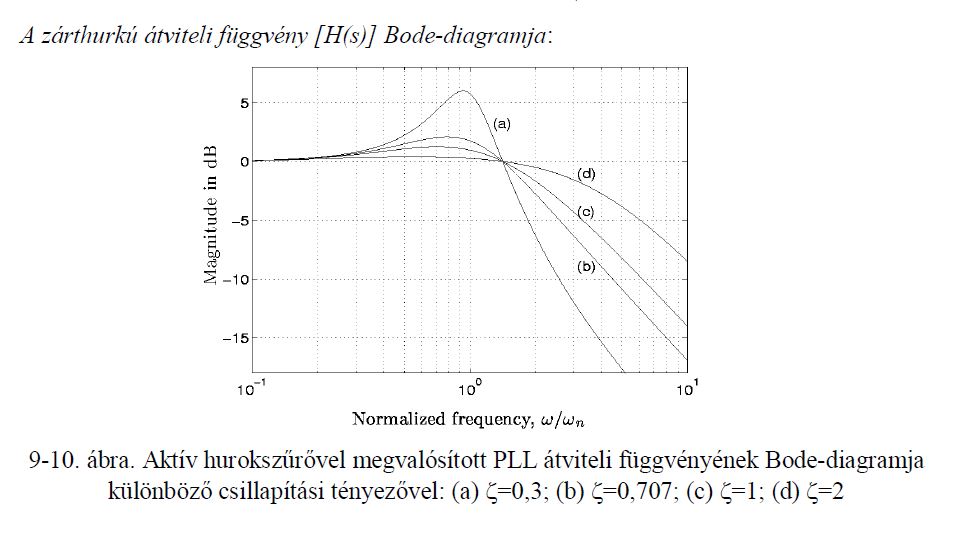
==17. Rajzolja fel a zárthurkú átviteli függvény Bode-diagramját különböző <math> \zeta </math>-ra.== | ==17. Rajzolja fel a zárthurkú átviteli függvény Bode-diagramját különböző <math> \zeta </math>-ra.== | ||
A lap 2014. február 7., 01:13-kori változata
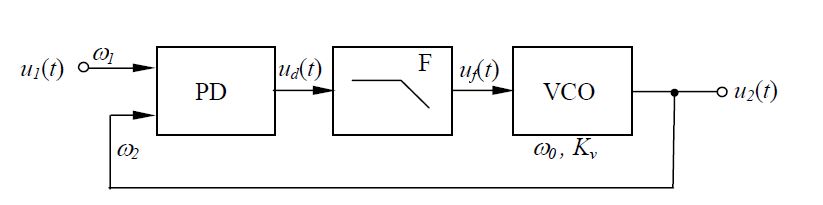
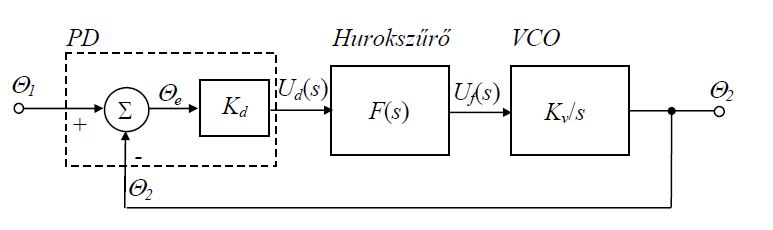
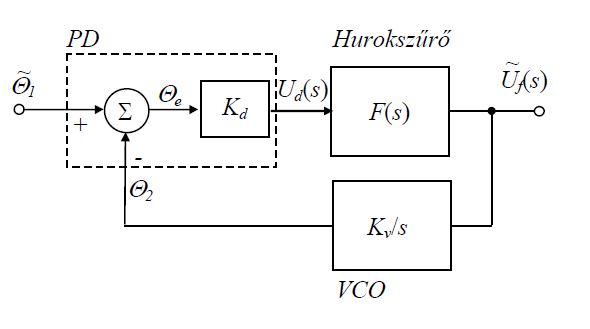
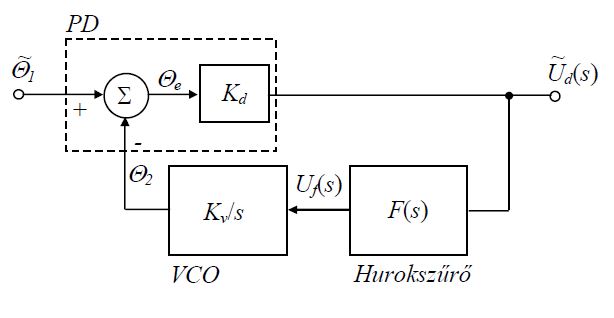
1. Rajzolja fel a PLL tömbvázlatát.
ahol a szabadonfutó frekvencia, pedig a VCO karakterisztikájának meredeksége
2. Adja meg a PD kimeneti feszültségét (nemlinearizált alak).
, ahol illetve a fázisdetektor bemeneteire jutatott jelek amplitudói, K a fázisdetektorra jellemző konstans, pedig a két jel fáziskülönbsége.
3. Adja meg a VCO kimeneti fázisát a komplex frekvenciatartományban.
, ahol a VCO átviteli tényezője, a bemenő jel komplex amplitudója.
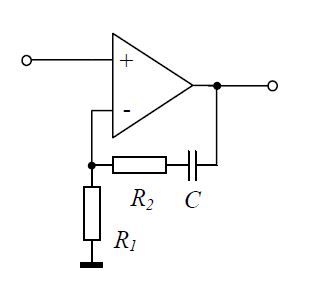
4. Rajzolja fel a hurokszűrő kapcsolási rajzát és adja meg az átviteli függvényét.
5. Adja meg a hurokszűrő átviteli függvényét és rajzolja fel a törtvonalas Bode-diagramját.
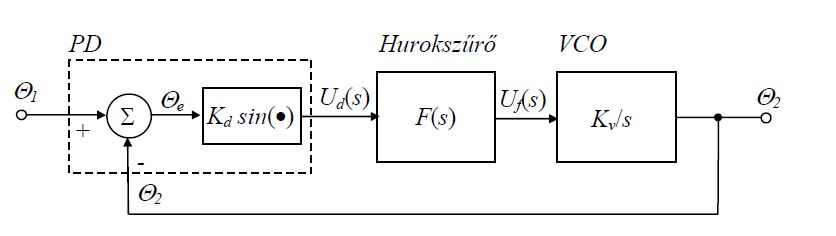
6. Rajzolja fel a PLL nemlineáris alapsávi modelljét.
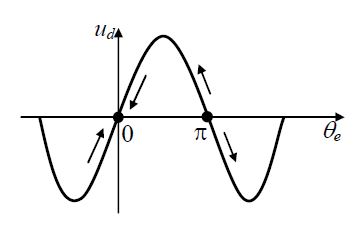
7. Rajzolja fel a PD nemlineáris karakterisztikáját és azon határozza meg a munkapontot.
Ha a fázishiba megnő, akkor ennek hatására megnő PD kimenetén a feszültség, majd a VCO pillantnyi kimeneti frekvenciája, ami egyben a PD egyik bemeneti jele. Ennek a jelnek úgy kell hatnia, hogy a fázishiba csökkenjen, ellenkező esetben nem jön létre fáziszárt állapot. A fenti elv a alpján a munkapont 0-ban van.
8. Adja meg a PLL bemenet és kimenete közti fáziskülönbség értékét. (aktív hurokszűrőre és fáziszárt állapotra értendő).
Mivel az alkalmazott aktív hurokszűrő erősítése nagy (kb. 200.00, mert nincs DC visszacsatolás), ezért a bementén csak közel 0V DC feszültség lehet. A hurokszűrő bemenete egyben a PD kimenete, és a PD kimenetén csak akkor lehet nulla fázishiba melett nulla feszültség, ha a két bemeneti jel között a fáziskülönbség , vagyis az egyik bemeneti jel szinusz, másik koszinusz.
9. Adja meg a PD kimeneti feszültségét a lineáris alapsávi modellben kis esetesetén (nem kell levezetni).
, ahol .
10. Rajzolja fel a PLL lineáris alpsávi modelljét.
11. Adja meg a hurokerősítés egyenletét (legegyszerűbb forma).
, ahol a hurokszűrő átviteli függvénye.
12. Adja meg a PLL zárthurkú átviteli függvényét (legegyszerűbb forma).
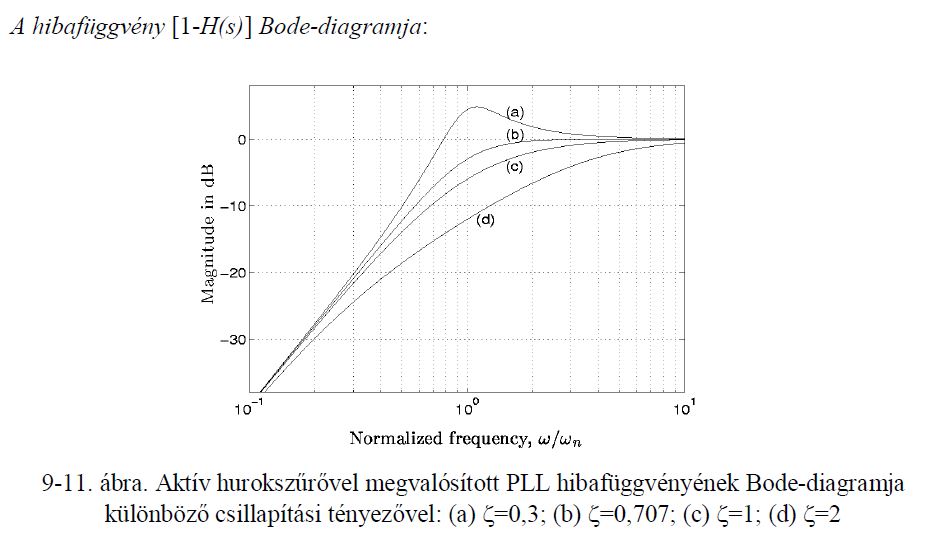
13. Adja meg a PLL hibafüggvényét (legegyszerűbb forma).
14. Adja meg a hurokerősítés egyenletét másodfokú hurokra (elsőfokú hurok, aktív hurokszűrővel).
, ahol a szűrő megfelelő időállandói
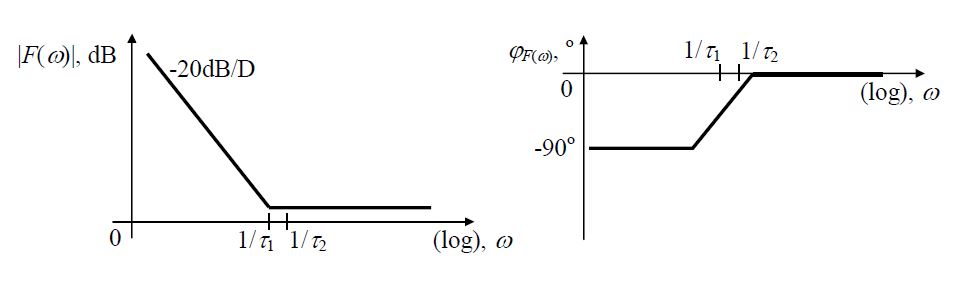
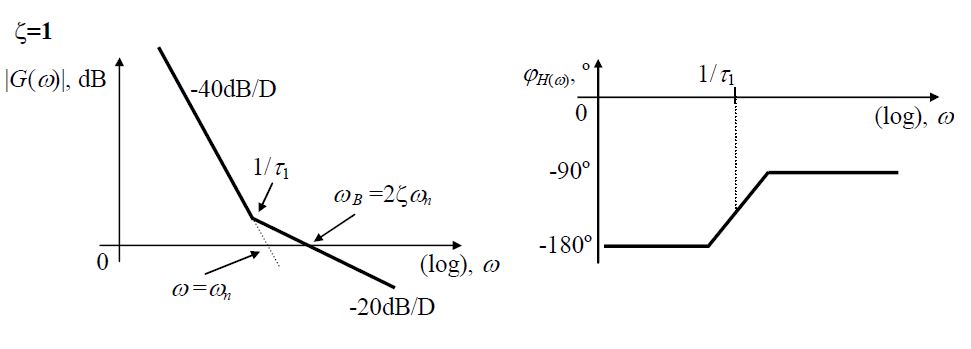
15. Rajzolja fel a hurokerősítés törtvonalas Bode-diagramját ().
16. Rajzolja fel a hurokerősítés törtvonalas Bode-diagramját ().
A 15. kérdés ábráján van ennek a kérdésnek a válasza is!
17. Rajzolja fel a zárthurkú átviteli függvény Bode-diagramját különböző -ra.
18. Rajzolja fel a hibafüggvény Bode-diagramját különböző -k esetén.
19. Adja meg a PLL tervezési paramétereit és, hogy az egyes paraméterek mit szabnak meg.
- a sávszélességet ()-t szabja meg,
- a stabilitási tulajdonságokat (-t), illetve a dinamikát szabja meg,
- a követési tulajdonságokat (-t) szabja meg (az alkalmazott aktív szűrőre
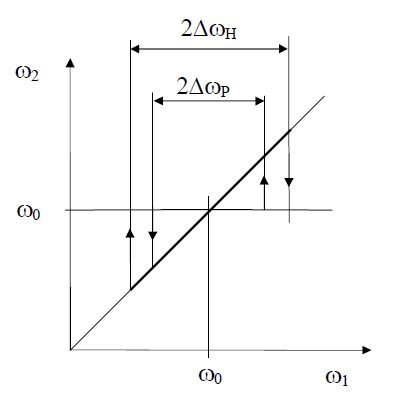
20. Adja meg a PLL frekvenciatartományait.
21. Rajzolja fel az FM demodulátor tömbvázlatát.
22. Milyen tervezési feltételt kell az FM demodulátornak kielégítenie?
maximális modulációs frekvencia, ahol a pólusfrekvencia.
23. Rajzolja fel a PM demodulátor tömbvázlatát.
24. Milyen tervezési feltételt kell a PM demodulátornak kielégítenie?
minimális modulációs frekvencia