„Laboratórium 2 - 3. Mérés ellenőrző kérdései” változatai közötti eltérés
| 263. sor: | 263. sor: | ||
A gyakorlatban adott frekvencián <math>\frac{U_\mathrm{ki}}{U_\mathrm{be}}</math> méréssel meghatározható, majd a képlettel <math>L_\mathrm{sz}</math> számítható. | A gyakorlatban adott frekvencián <math>\frac{U_\mathrm{ki}}{U_\mathrm{be}}</math> méréssel meghatározható, majd a képlettel <math>L_\mathrm{sz}</math> számítható. | ||
==12. | ==12. Elektromágneses tereknél mit nevezünk közeltérnek illetve távoltérnek?== | ||
Elektromágneses tereknél mit nevezünk közeltérnek illetve távoltérnek? | |||
Ábra: | Ábra: | ||
| 289. sor: | 283. sor: | ||
<math>\vec{H}</math> ismeretében konkrét esetben <math>\vec{E}</math> rotációképzéssel számítható, de <math>\vec{E}</math> -re is megadható az előbbihez hasonló összefüggés, de az jóval bonyolultabb. Ennek is van egy távoli, az áram deriváltjával és <math>\frac{1}{R}</math>-rel arányos, egy közeli, az árammal és <math>\frac{1}{R^2}</math>-tel arányos összetevője, de van még egy harmadik, még közelebbi, <math>\frac{1}{R^3}</math> szerint eltűnő és az áram idő szerinti integráljával (a töltéssel) arányos összetevője is. | <math>\vec{H}</math> ismeretében konkrét esetben <math>\vec{E}</math> rotációképzéssel számítható, de <math>\vec{E}</math> -re is megadható az előbbihez hasonló összefüggés, de az jóval bonyolultabb. Ennek is van egy távoli, az áram deriváltjával és <math>\frac{1}{R}</math>-rel arányos, egy közeli, az árammal és <math>\frac{1}{R^2}</math>-tel arányos összetevője, de van még egy harmadik, még közelebbi, <math>\frac{1}{R^3}</math> szerint eltűnő és az áram idő szerinti integráljával (a töltéssel) arányos összetevője is. | ||
[[Category:Villanyalap]] | [[Category:Villanyalap]] | ||
A lap 2014. február 3., 14:04-kori változata
1. Végtelen hosszú egyenes vezető mágneses tere
Egy végtelen hosszú, szinuszos áramot szállító vezetőtől távolságban lévő pontban határozza meg a térerősséget és a indukciót!
Megoldás:
Ábra:
Ampere-féle gerjesztési törvényt felírva egy olyan zárt L görbére, amely által kifeszített, a vezetékre merőleges A körlapot a vezeték pont a közepén döfi át:
Szimmetria okokból, a mágneses térerősségvektorok a görbe mentén mindenhol érintő irányúak, így a vonalintegrál egy egyszerű szorzássá egyszerűsödik. Az elektromos eltolásvektor időbeli változása zérus, az áramsűrűségvektor pedig merőleges az A körlapra, a felületintegrál eredménye az A körlapon átfolyó áramerősség:
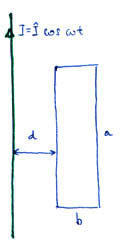
2. Végtelen hosszú egyenes vezető környezetében elhelyezkedő vezetőkeretben indukált feszültség meghatározása
Egy végtelen hosszú, szinuszos áramot szállító vezető síkjában egy téglalap alakú, méretű vezetőkeret helyezkedik el. A vezetőkeret méretű oldala párhuzamos az áramot szállító vezetővel. Határozza meg a vezetőkeretben indukált feszültséget!
Megoldás
Ábra:
A Faraday-féle indukciós törvény felhasználásával:
Az integrálást tehát csak a oldal szerint végezzük el, mivel oldal mentén a mágneses térerősség állandó. A keret távolsága a vezetőtől .
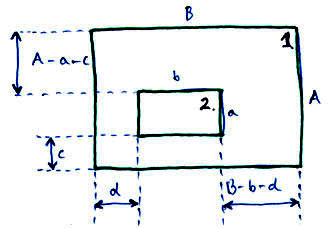
3. Vezetőkeretben indukált feszültség és kölcsönös induktivitás meghatározása
Egy téglalap alakú, méretű, szinuszos áramot szállító vezetőkeret síkjában, a kereten belül egy második, méretű kisebb vezetőkeret aszimmetrikusan helyezkedik el. Az és illetve és méretű oldalak párhuzamosak. A legegyszerűbb modell alapján becsülve, közelítőleg mekkora feszültség indukálódik a második keretben? Mekkora a kölcsönös induktivitás?
Megoldás
Ábra:
Az alkalmazott modellben a külső keret által a belső keretben indukált feszültséget oly módon számítjuk, hogy a külső keret oldalait külön-külön, végtelen hosszú vezetőnek tekintjük, így felhasználható az előző kérdés megoldása:
A belső vezetőkeretben indukált feszültség a Faraday-féle indukciós térvénnyel egyszerűen számítható:
A kölcsönös induktivitás definíció szerint számítható:
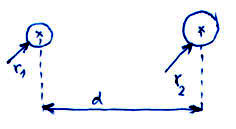
4. Határozza meg két végtelen hosszú, párhuzamosan futó hengeres vezető között a hosszegységre eső villamos kapacitást!
Ábra:
Vezessük be az alábbi jelöléseket:
- és
- Az sugarú vezetőhenger egységnyi hosszúságú szakaszára eső töltés
- Az sugarú vezetőhenger egységnyi hosszúságú szakaszára eső töltés
Egy töltött sugarú hengeres vezető által keltett elektromos térerősségvektor a Gauss-tétellel meghatározható, ha azt egy hosszúságú sugarú felületű koaxiális hengerre írjuk fel.
Szimmetria okok miatt az elektromos térerősségvektor mindig sugárirányú lesz, így a henger lapjain az integrál értéke zérus, míg hengerpaláston egy egyszerű szorzássá egyszerűsödik.
Az sugarú henger töltése potenciálkülönbséget hoz létre a két henger között.
Az sugarú henger töltése potenciálkülönbséget hoz létre a két henger között. Hasonló számítással adódik, hogy:
MIvel a potenciáltér lineáris, így a két henger közötti potenciálkülönbség:
A két hengeres vezető közötti hosszegységre eső kapacitás definíció szerint:
Ha mindkét henger azonos sugarú, azaz , abban az esetben:
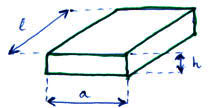
5. Határozza meg nyomtatott huzalozás esetén egy vezetőszakasz ellenállását és annak bizonytalanságát!
Ábra:
Ahol a fajlagos ellenállás, a vezetékszakasz hossza, a szélessége, pedig a vastagsága.
A hibakomponensek worst case összegzése esetén:
A hibakomponensek valószínűségi összegzésével, ami a tényleges bizonytalanságot adja:
6. Tanulmányozza a CD11.4599.151 típusú hálózati szűrő működését és műszaki adatait!
A CD11.4599.151 típusú szűrővel rendelkező hálózati csatlakozó 2 pólusú kapcsolója lengő vezetéken helyezkedik el. Névleges áramerőssége 1A, általános célú berendezésekbe tervezték, 1 pólusú beépített olvadóbiztosítékkal.
A belső elemek értékei: L= 2 x 10 mH, Cx = 68 nF, Cy = 2,2 nF.
A Cx és Cy kondenzátorok szigorú szabványok alapján tervezett, öngyógyuló dielektrikumos fóliakondenzátorok.
A szűrő kettős feladatot lát el:
- Az eszközre jutó feszültségcsúcsok ellen véd, amelyet elektromechanikus kapcsolók illetve relék okozhatnak.
- Ugyanez a szűrő a másik irányban is működik, az eszköz által keltett nagyfrekvenciás zavarokat csillapítja.
A zavarok fajtái:
A) Feszültségingadozások
B) Harmónikus frekvenciájú inerferencia (100 Hz - 2 kHz)
C) Tranziensek által okozott interferencia (300 MHz-ig)
D) Szinusz szerű zavarok (akár 1 GHz-ig)
A szűrők alkotóelemei általában kondenzátorok és tekercsek, de gyakran alkalmaznak kondenzátor-kisütő ellenállásokat, túlfeszültség-védőket és igen nagyfrekvenciás fojtókat is. Emiatt a szűrő általában több egymást követő fokozatból áll.
A zavarok terjedhetnek közvetlen vezetéssel, kapacitív és induktív csatolással valamint sugárzással.
A zavarokat feloszthatjuk közös és differenciális módusú zavarokra. Földeletlen zavarforrásból származó zavaró jel a tápáramhoz hasonló módon, az egyik vezetéken befolyik az eszközbe, a másikon pedig ki. Ezt nevezzük differenciális módusú zavaró jelnek. A közös módusú zavar ezzel szemben (a mechanikai kialakítás következtében) mindkét tápvezetéken folyik be az eszközbe, és a földelésen folyik vissza a zavarforráshoz.
A közös módusú zavarok csillapítása --> ld. 7. kérdés
A differenciális módusú zavarokat a fojtó csak kismértékben csillapítja (ld. 7. kérdés), ezért van szükség a Cy kondenzátorok beépítésére, amelyek viszont a védővezetőbe folyó (úgynevezett szivárgási) áramot okoznak. Ha a szivárgási áramra vonatkozó követelmény szigorú, ezeket el kell hagyni (pl. orvosi célú szűrők, melyekben a nagy Cx kapacitás kisütésére még egy ellenállást is beépítenek, hogy a táplálatlan szűrő kimenetén ne maradhasson fenn az üzemi feszültség).
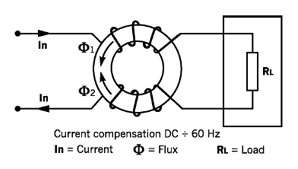
7. A szűrő közös vasmagon elhelyezett két tekercsének milyen a menetirányítása és miért?
A szűrő egy rádiófrekvenciás áramkompenzált fojtó (angolul RF Current Compensated Suppression Choke). A tekercsei úgy vannak irányítva, hogy a rajtuk folyó üzemi áramok által létrehozott fluxusok ellentétes irányúak legyenek, így kioltsák egymást. Ezek alapján, az áramirányok figyelembevételével mondhatjuk, hogy a tekercsek menetirányítása ellentétes.
Emiatt a differenciális módusú zavarok által keltett fluxusok (ideális esetben, azaz tökéletes csatolást feltéve) kioltják egymást. A közös módusú zavarok által keltett fluxusok viszont egyirányúak, így az ilyen zavarokat a fojtó szűrni tudja. A valóságban viszont a laza csatolás miatt fellépő szórási fluxus következtében a differenciális módusú zavarok kismértékű csillapítására is képes.
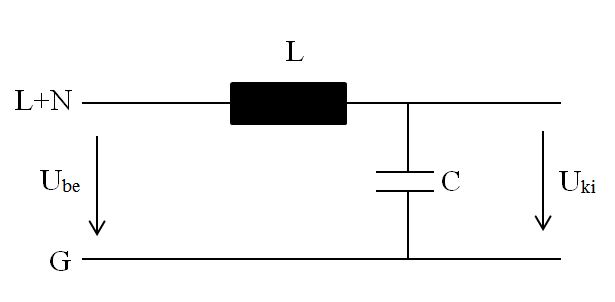
8. Adja meg a szűrő aszimmetrikus zavarjelre érvényes modelljét!
Az aszimmetrikus zavarjelekre (közös módusú zavarokra) érvényes modell: (L1 = L2 = 10 mH, Cy = 2,2 nF)
9. Ideális elemeket feltételezve írja fel a szűrő csillapítását aszimmetrikus zavarjelre!
Ábra:
10. Adja meg a szűrő szimmetrikus zavarjelre érvényes modelljét!
11. Ideális elemeket feltételezve írja fel a szűrő csillapítását szimmetrikus zavarjelre!
Ideális eset: (szivárgási induktivitás) A csillapítás egységnyi, a kimeneti feszültség bármely frekvencián megegyezik a bemeneti feszültséggel.
Valóságban:
A gyakorlatban adott frekvencián méréssel meghatározható, majd a képlettel számítható.
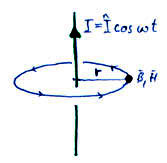
12. Elektromágneses tereknél mit nevezünk közeltérnek illetve távoltérnek?
Ábra:
A vonalszerű vezetőben folyó áram által létrehozott mágneses térerősséget az általánosított Biot-Savart törvény adja meg:
Ebből kiolvasható, hogy az összefüggés első tagja az árammal arányos és a távolság négyzetével fordítottan arányos. A mágneses térerősségnek e tag által leírt komponensét közeltérnek vagy közeli térnek nevezzük.
Az összefüggés második tagja ellenben az áram idő szerinti deriváltjával arányos, és a távolsággal (és nem a négyzetével) fordítottan arányos. Ezt az összetevőt távoltérnek vagy távoli térnek nevezzük.
Tehát a vezetőhöz közel a közeli, messze a távoli tér a domináns. Az áram idő szerinti deriváltjával való arányosság szemléletesen úgy is leírható, hogy adott nagyságú áram esetén adott távolságra a vezetéktől a távoltér annál nagyobb a közeltérnél, minél nagyobb az I áram frekvenciája. Tehát előírt erőteret annál kisebb árammal tudunk létrehozni, minél nagyobb frekvenciát választunk.
ismeretében konkrét esetben rotációképzéssel számítható, de -re is megadható az előbbihez hasonló összefüggés, de az jóval bonyolultabb. Ennek is van egy távoli, az áram deriváltjával és -rel arányos, egy közeli, az árammal és -tel arányos összetevője, de van még egy harmadik, még közelebbi, szerint eltűnő és az áram idő szerinti integráljával (a töltéssel) arányos összetevője is.