„Szabályozástechnika - Diszkrétidejű állapotteres szabályozók tervezése” változatai közötti eltérés
A VIK Wikiből
aNincs szerkesztési összefoglaló |
|||
| 48. sor: | 48. sor: | ||
<syntaxhighlight lang="matlab" style="font-size: 140%;"> | <syntaxhighlight lang="matlab" style="font-size: 140%;"> | ||
% Az állapotteres szabályzás alapelve, hogy a zárt körben előre meghatározott pólusokat szeretnénk. | |||
% Ezek általában egy domináns komplex konjugált póluspár (zdom1 és zdom2 - ez határozza meg a tranzienseket), | |||
% és megfelelő számú, a domináns póluspárnál 3-5ször gyorsabb pólus (zcinf). | |||
% Ezekből a segédpólusokból n-2 darabra van szükség, ahol n az állapotváltozók száma. | |||
% Ezt a kívánt póluselrendezést úgy érhetjük el, hogy a bemenetre egy K erősítésvektoron keresztül negatívan | |||
% visszacsatoljuk az állapotváltozókat, azaz u = -K*x. Ha ezt behelyettesítjük a rendszer állapotegyenletébe, | |||
% akkor x[k+1] = Phi*x[k] + Gamma*u[k] = Phi*x[k] + Gamma*(-K*x[k]) = (Phi-Gamma*K)*x[k] lesz a módosult | |||
% rendszer állapotegyenlete. Látható hogy úgy kell a K értékét megválasztani, hogy az Phi-Gamma*K módosult | |||
% rendszermátrix sajátértékei éppen az általunk előírt pólusok legyenek. Az ehhez szükséges K erősítés | |||
% SOR-vektor az Ackermann képlettel egyszerűen meghatározható. | |||
% | |||
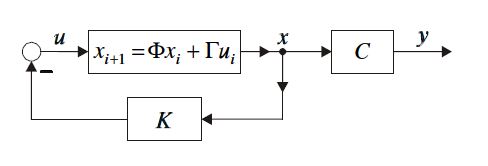
% Az állapot-visszacsatolást tartalmazó szabályzó hatásvázlata: | % Az állapot-visszacsatolást tartalmazó szabályzó hatásvázlata: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| 66. sor: | 77. sor: | ||
sdom2=conj(sdom1); | sdom2=conj(sdom1); | ||
% Áttérés z-re | % Áttérés z-re az ismert z = exp(s*Ts) képlet alapján | ||
zdom1=exp(sdom1*Ts); | zdom1=exp(sdom1*Ts); | ||
zdom2=exp(sdom2*Ts); | zdom2=exp(sdom2*Ts); | ||
| 74. sor: | 85. sor: | ||
% akkor n-2 multiplicitással a zcinf pólusok is | % akkor n-2 multiplicitással a zcinf pólusok is | ||
phic=[zdom1 zdom2]; | phic=[zdom1 zdom2]; | ||
% A zárt kör karakterisztikus polinomja | |||
polyphic=poly(phic); | |||
% Az irányíthatóság ellenőrzése | % Az irányíthatóság ellenőrzése | ||
A lap 2014. január 12., 19:01-kori változata
Simulink modellek
- Töltsd le!
- Csomagold ki!
- Másold be a Matlab aktuális munkakönyvtárába!
A mechanikai lengőrendszer leírása
%% Állapotteres szabályozás diszkrét időben
%% Mechanikai lengőrendszer leírása
% A rendszer paraméterei
m=2; % A test tömege
k=0.75; % Rugóállandó
b=0.25; % Csillapítás
% A folytonos idejű állapotteres leírás mátrixai:
Ac = [0 1; -k/m -b/m]
Bc = [0; 1/m]
Cc = [1 0]
Dc = 0
sys=ss(Ac,Bc,Cc,Dc); % A folytonos idejű rendszer összeállítása
Ts=0.2; % Mintavételi idő
dsys=c2d(sys,Ts,'zoh'); % Áttérés diszkrét időre
step(sys,dsys); % A folytonos és diszkrét idejű rendszer ugrásválasza
% A diszkrét idejű állapotteres leírás mátrixai:
[Phi,Gamma,C,D]=ssdata(dsys)
Állapotvisszacsatolás tervezése
% Az állapotteres szabályzás alapelve, hogy a zárt körben előre meghatározott pólusokat szeretnénk.
% Ezek általában egy domináns komplex konjugált póluspár (zdom1 és zdom2 - ez határozza meg a tranzienseket),
% és megfelelő számú, a domináns póluspárnál 3-5ször gyorsabb pólus (zcinf).
% Ezekből a segédpólusokból n-2 darabra van szükség, ahol n az állapotváltozók száma.
% Ezt a kívánt póluselrendezést úgy érhetjük el, hogy a bemenetre egy K erősítésvektoron keresztül negatívan
% visszacsatoljuk az állapotváltozókat, azaz u = -K*x. Ha ezt behelyettesítjük a rendszer állapotegyenletébe,
% akkor x[k+1] = Phi*x[k] + Gamma*u[k] = Phi*x[k] + Gamma*(-K*x[k]) = (Phi-Gamma*K)*x[k] lesz a módosult
% rendszer állapotegyenlete. Látható hogy úgy kell a K értékét megválasztani, hogy az Phi-Gamma*K módosult
% rendszermátrix sajátértékei éppen az általunk előírt pólusok legyenek. Az ehhez szükséges K erősítés
% SOR-vektor az Ackermann képlettel egyszerűen meghatározható.
%
% Az állapot-visszacsatolást tartalmazó szabályzó hatásvázlata:
% Gyorsabb, de jobban csillapított zárt kört szeretnénk - az előírásokat
% folytonos időben adjuk meg!
w0=1;
xi=0.8;
% A zárt kör sajátértékei s-ben
% Ha a rendszernek 2-nél több állpotváltozója van, akkor n-2 segédpólust
% (scinf) is fel kell vennünk, melyek 3-5ször gyorsabbak mint a domináns póluspár.
sdom1=-w0*xi+j*w0*sqrt(1-xi^2);
sdom2=conj(sdom1);
% Áttérés z-re az ismert z = exp(s*Ts) képlet alapján
zdom1=exp(sdom1*Ts);
zdom2=exp(sdom2*Ts);
% zcinf=exp(scinf*Ts);
% A zárt kör sajátértékeit tartalmazó vektor, valamint ha n>2,
% akkor n-2 multiplicitással a zcinf pólusok is
phic=[zdom1 zdom2];
% A zárt kör karakterisztikus polinomja
polyphic=poly(phic);
% Az irányíthatóság ellenőrzése
Mc=ctrb(Phi,Gamma); % Az irányíthatósági mátrix...
rank(Mc) % ... és rangja
% Ha rank(Mc)=n, akkor a rendszer irányítható
% Állapotvisszacsatolás tervezése az Ackermann-képlet segítségével
K=acker(Phi,Gamma,phic)
% A megfelelő Simulink-modell megnyitása
open('discrete_1');
% Ugyanaz az feladat, mint a folytonos esetben...
% VIGYÁZAT: Minden építőelemnél, ami nem a szakasz része, meg kell
% adni a Ts mintavételi periódusidőt!!!
% Várakozás billentyűlenyomásra
pause
Alapjel miatti korrekció
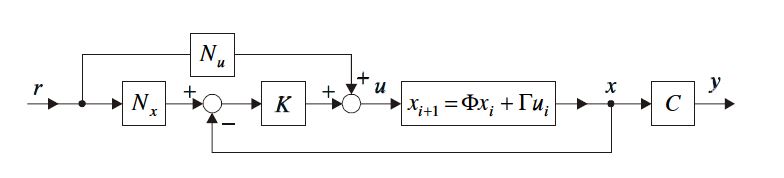
% Az alapjel miatti korrekciót is tartalmazó szabályzó hatásvázlata:
% Tervezés
% FIGYELEM: Eltérés a folytonos időtől, hogy itt Phi-eye(n) szerepel első elemként.
% Az oszlopvektorban n darab nulla és fixen 1 darab egyes.
N=inv([Phi-eye(2) Gamma; C 0])*[0;0;1];
% Az Nx-et és Nu-t tartalmazó vektor szétválasztása
Nx=N(1:2) % Annyi elem, ahány állapotunk van (n)
Nu=N(end) % Skalár
% A megfelelő Simulink-modell megnyitása
open('discrete_3');
% Várakozás billentyűlenyomásra
pause
Állapotmegfigyelő tervezése
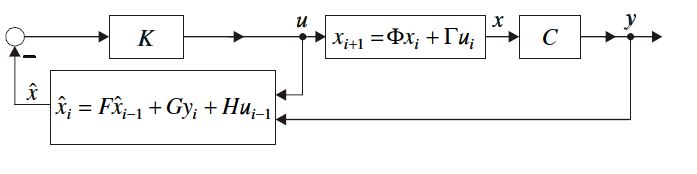
% Az állapotmegfigyelőt is tartalmazó állapot-visszacsatolásos szabályzó hatásvázlata:
% A megfigyelő sajátértéke s-ben
soinf=-5
% Áttérés z-tartományra
zoinf=exp(soinf*Ts);
% A megfigyelő karakterisztikus gyökei: soinf megfelelő multiplicitással (n)
phio=[zoinf zoinf]
% A megfigyelhetőség ellenőrzése
Mo=obsv(Phi,C); % A megfigyelhetőségi mátrix...
rank(Mo) % ... és rangja
% Ha rank(Mo)=n, akkor a rendszer megfigyelhető
% Megfigyelő tervezése - VIGYÁZAT: Itt a paraméterezés nem analóg a folytonos esettel!
G=acker(Phi',Phi'*C',phio)'
F=Phi-G*C*Phi
H=Gamma-G*C*Gamma;
% A megfelelő Simulink-modell megnyitása
open('discrete_2');
% VIGYÁZAT: Itt nem lehet discrete state space objektumként megadni az állapotmegfigyelőt!
% Elemenként kell azt összeraknunk azt, a differenciaegyenlete alapján!
%
% ^ ^
% x[k] = F * x[k-1] + G * y[k] + H * u[k-1]
% FIGYELEM: Mivel aktuális megfigyelőt terveztünk, így az y[k] nincs késleltetve!
% Várakozás billentyűlenyomásra
pause
Terhelésbecslő tervezése
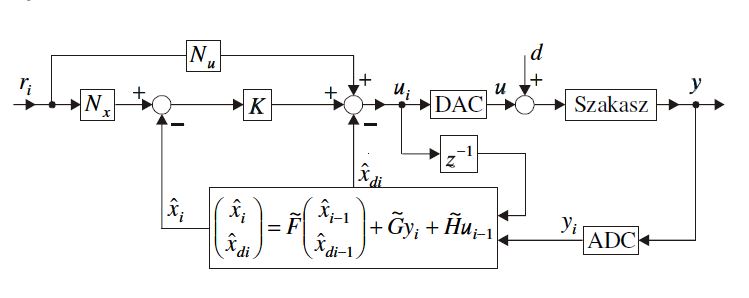
% Az terhelésbecslővel kiegészített szabályzó hatásvázlata:
% A kibővített rendszer mátrixai
Phitilde=[Phi Gamma; 0 0 1]; % n darab nulla és fixen 1 darab egyes (SISO)
Gammatilde=[Gamma;0]; % Fixen 1 darab nulla a végére (SISO)
Ctilde=[C 0]; % Fixen 1 darab nulla a végére (SISO)
% A megfigyelő sajátértékeit tartalmazó vektorban soinf most egyel nagyobb
% multiplicitással szerepel, hiszen felvettünk egy új (fiktív) állapotot
phiotilde=[zoinf zoinf zoinf];
% Megfigyelőtervezés a kibővített rendszerhez
% Ugyanaz, mint az állapotmegfigyelőnél, csak most a 'tilde rendszerre
Gtilde=acker(Phitilde',Phitilde'*Ctilde',phiotilde)'
Ftilde=Phitilde-Gtilde*Ctilde*Phitilde;
Htilde=Gammatilde-Gtilde*Ctilde*Gammatilde;
% A megfelelő Simulink-modell megnyitása
open('discrete_4');
% Várakozás billentyűlenyomásra
pause
Integráló szabályozás tervezése
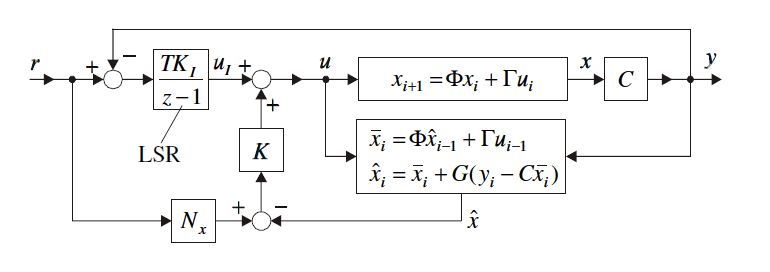
% Az integráló hatást is tartalmazó szabályzó hatásvázlata:
% A kibővített rendszer mátrixai
% n*1-es nullmátrix, a végén fixen 1 darab egyes (SISO)
Phii=[Phi zeros(2,1);C*Ts 1];
Gammai=[Gamma;0];
% Az integrátor állapotának s=-3-nak megfelelő sajátértéket írunk elő
phictilde=[zdom1 zdom2 exp(-3*Ts)];
% Állapotvisszacsatolás számítása
Ktilde=acker(Phii,Gammai,phictilde);
% Az állapotvisszacsatolás vektorának felbontása
Kt=Ktilde(1:2); % Annyi eleme van, ahány valódi állapotunk
Ki=Ktilde(3); % Skalár
% A megfelelő Simulink-modell megnyitása
open('discrete_5');
% Ebben nincs terhelésbecslő, hiszen mind a terhelésbecslő, mind
% az integrátor zavarelnyomási célokat szolgál, így a kettő együtt felesleges
% Várakozás billentyűlenyomásra
pause