„Laboratórium 1 - 2009 őszi ZH megoldások” változatai közötti eltérés
a David14 átnevezte a(z) Labor 1. 2009 ZH-k lapot a következő névre: Laboratórium 1 - 2009 őszi ZH megoldások |
aNincs szerkesztési összefoglaló |
||
| 1. sor: | 1. sor: | ||
== 1. Feladat == | |||
'''Egy <math> 50 \Omega </math> kimeneti ellenállású generátor üresjárási feszültségének effektív értéke <math> U_g=5V </math>. A jelalak szinuszos, a jel frekvenciája <math> f = 1kHz </math>. A generátor jelét egy <math> l = 0,5m </math> hosszú, <math>Z_0=50 \Omega </math> hullámimpedanciájú kábellel digitális feszültségmérőre vezetjük.''' | |||
'''a) Rajzolja fel a mérési elrendezés modelljét! Mekkora a feszültségmérőre kerülő jel csúcstól csúcsig (<math> U_{pp} </math>) értéke?''' | |||
= | <math>u(t,l)=U_g \cdot \frac{Z_g}{Z_0+Z_g} \cdot (1+r_l)[1(t-T)+r_l \cdot r_g \cdot 1(t-3T)+(r_l \cdot r_g)^2 \cdot 1(t-5T)+\ldots{}]</math> Ezt csak azért írom ide, mert meglehet oldani ezzel is, ezt vettük elektronika 2-ből. | ||
Másképpen: kis vezetékeknél (a hullámhosszhoz képest) a bemeneti impedancia meg fog egyezni a vezeték végén lévő terheléssel (jelen esetben szakadás ,mert a volt mérőnek nagyon nagy a bementi impedanciája) illetve a mért feszültségek mindkét helyen közel (nagyon pici különbség) egyformák, így <math> U=5 \cdot \frac{Z_be}{Z_g+Z_be}=5V</math>. Mivel ez effektív érték így az <math>U_{pp}=5 \cdot \sqrt{2} \cdot 2</math>. | |||
Másképpen: kis vezetékeknél (a hullámhosszhoz képest) a bemeneti impedancia meg fog egyezni a vezeték végén lévő terheléssel (jelen esetben szakadás ,mert a volt mérőnek nagyon nagy a bementi impedanciája) | |||
'''b) A jelet a fenti kábellel egy <math> R_{be} </math> = <math> 50 \Omega </math> bemeneti ellenállású eszközre vezetjük. Rajzolja fel ismét a mérési elrendezés modelljét és adja meg a bemenetre kerülő jel <math> U_{pp} </math> értékét!''' | |||
Ugyanaz mint az első résznél, csak <math>Z_{be} = 50 \Omega </math> , tehát <math> U=5 \cdot \frac{Z_be}{Z_g+Z_be}=2,5V</math>. Így az <math>U_{pp}=2,5 \cdot \sqrt{2} \cdot 2</math>. | |||
== 2. Feladat == | |||
'''<math>Z_0=50 \Omega</math> hullámimpedanciájú <math> l=100m </math> hosszúságú kábelt hajtunk meg egy <math>50 \Omega</math> impedanciájú impulzusgenerátorral. Az elektromágneses hullám terjedési sebessége a kábelen előzetes mérések alapján <math> v = 2*10^8 m/s </math>. A kábelt szakadással "zárjuk le".''' | |||
'''a) Mekkora lehet az impulzus maximális szélesség, hogy a kábel bemenetén ne lapolódjon át az eredeti és a reflektált impulzus?''' | |||
Szakadással zárjuk le, <math> \gamma = 1, T_k=\frac{l}{v} = 5*10^{-7}s = 0,5\mu s </math>, tehát 1 <math>\mu</math>s telik el míg a jel eljut a bemenettől a lezárásig és onnan visszaér a bemenethez, tehát ez a maximális impulzusszélesség is. | Szakadással zárjuk le, <math> \gamma = 1, T_k=\frac{l}{v} = 5*10^{-7}s = 0,5\mu s </math>, tehát 1 <math>\mu</math>s telik el míg a jel eljut a bemenettől a lezárásig és onnan visszaér a bemenethez, tehát ez a maximális impulzusszélesség is. | ||
'''b) Mekkora lehet az impulzus maximális szélessége akkor, ha rövidzárral zárjuk le a kábelt?''' | |||
Rövidzárral zárjuk le, <math> \gamma = -1 </math> | Rövidzárral zárjuk le, <math> \gamma = -1 </math> | ||
| 31. sor: | 27. sor: | ||
A <math>T_k</math> nem változik tehát a végeredmény ugyanaz, 1 <math>\mu</math>s. | A <math>T_k</math> nem változik tehát a végeredmény ugyanaz, 1 <math>\mu</math>s. | ||
==== | == 3. Feladat == | ||
'''Adott egy 10kHz frekvenciájú periodikus jel. Alapharmonikusának amplitúdója 2V, 10. felharmonikusának amplitúdója 10mV (a többi harmonikus elhanyagolható). A jelet a frekvenciatartományban FFT segítségével vizsgáljuk. A mintavételezés koherens.''' | |||
'''a) Hány dB különbséget mérünk a két harmonikus amplitúdója között?''' | |||
<math> 20\lg \frac{2}{10 * 10^{-3}}= 46dB </math> | <math> 20\lg \frac{2}{10 * 10^{-3}}= 46dB </math> | ||
'''b) Hozzávetőlegesen hány dB lesz a különbség a két amplitúdó között, ha a jelet transzformáció előtt egy elsőfokú, 100Hz törésponti frekvenciájú aluláteresztő szűrőre vezetjük? Rajzolja be külön ábrába minőségileg helyesen a szűrő amplitúdókarakterisztikáját, valamint a jel spektrumát!''' | |||
Az aluláteresztő szűrő a törésponti frekvenciája után 20dB-lel csökkenti az amplitúdót dekádonként. | Az aluláteresztő szűrő a törésponti frekvenciája után 20dB-lel csökkenti az amplitúdót dekádonként. | ||
| 51. sor: | 49. sor: | ||
|} | |} | ||
Az arány: | Az arány: <math> 20\lg \frac{0.02}{10 * 10^{-6}}= 66 dB </math> | ||
<math> 20\lg \frac{0.02}{10 * 10^{-6}}= 66 dB </math> | |||
Megjegyzés: | Megjegyzés: Úgy is lehet gondolkozni, hogy az alapharmonikust 40dB-lel csökkenti, a felharmonikust 60dB-lel, tehát a kettő közötti különbség 20dB-lel nő, azaz a 46dB+20dB=66dB | ||
== 4. Feladat == | |||
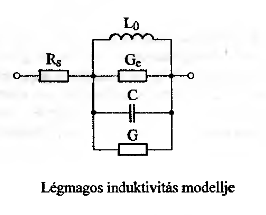
'''Adja meg egy légmagos és egy vasmagos tekercs modelljét! Ismertesse a modell paramétereit és azok fizikai hátterét!''' | |||
[[Fájl:Labor1 kép22.bmp]] | |||
{| border="1" | {| border="1" | ||
| 73. sor: | 70. sor: | ||
| <math> R_S </math> || soros rézellenállás | | <math> R_S </math> || soros rézellenállás | ||
|} | |} | ||
<math> L=\frac{L_0}{1-{\omega}^2L_0 C} </math> | <math> L=\frac{L_0}{1-{\omega}^2L_0 C} </math> | ||
Méréstechnika példatár: 7.17 feladat megoldása (172.oldal). Van egy párhuzamosan Rv és L és ezzel sorban egy Rs. | Méréstechnika példatár: 7.17 feladat megoldása (172.oldal). Van egy párhuzamosan Rv és L és ezzel sorban egy Rs. | ||
{| border="1" | {| border="1" | ||
| 86. sor: | 85. sor: | ||
|} | |} | ||
==== | == 5. Feladat == | ||
'''Párhuzamos RC-tag in-circuit vizsgálatát végezzük. R = <math> 10k \Omega </math> +-1%, C = 100nF +- 1%. Mekkora legyen a mérési frekvencia és az impedanciamérő mérési bizonytalansága?''' | |||
<math> R_e = R \times \frac{1}{\omega C} </math> | <math> R_e = R \times \frac{1}{\omega C} </math> | ||
<math> Tipp: \omega = \frac{1}{RC} = 1000 \frac{rad}{s} </math> | <math> Tipp: \omega = \frac{1}{RC} = 1000 \frac{rad}{s} </math> | ||
== 6. Feladat == | |||
'''Adott az alábbi logikai hálózat. A hálózatot 10kHz-es négyszögjellel gerjesztjük.''' | |||
[[Fájl:Labor1 kép23.gif]] | |||
'''a) Rajzolja fel a gerjesztőjel és a "mérőpont 1"-en mérhető jel hullámformáját!''' | |||
Elvileg késleltet két inverterkésleltetési időnyit, a jelalakot a kondi megváltoztatja, mert a négyszögjel végtelen sok szinusz összege, és a kondenzátor végtelen frekvencián rövidzárként viselkedik, tehát egy "szűrő". Így a nagyfrekvenciás komponensek nem jelennek meg, nem lesz annyira négyszöges. | Elvileg késleltet két inverterkésleltetési időnyit, a jelalakot a kondi megváltoztatja, mert a négyszögjel végtelen sok szinusz összege, és a kondenzátor végtelen frekvencián rövidzárként viselkedik, tehát egy "szűrő". Így a nagyfrekvenciás komponensek nem jelennek meg, nem lesz annyira négyszöges. | ||
'''b) Hogyan befolyásolja a kondenzátor a "mérőpont 2"-n mérhető felfutási időt (rise time)?''' | |||
Bár a kondi elrontja a négyszögjelet, emiatt a komparálási feszültséget később éri el a felfutó ill. lefutó él, így megnő a késleltetés. Ugyanakkor az inverterek a kondi után a négyszögjelet visszaállítják. A felfutási idő nem növekszik a mérőpont2-n (hála az invertereknek), csak késni fog, mert később éri el a komparálási feszültséget a jel. | Bár a kondi elrontja a négyszögjelet, emiatt a komparálási feszültséget később éri el a felfutó ill. lefutó él, így megnő a késleltetés. Ugyanakkor az inverterek a kondi után a négyszögjelet visszaállítják. A felfutási idő nem növekszik a mérőpont2-n (hála az invertereknek), csak késni fog, mert később éri el a komparálási feszültséget a jel. | ||
'''c) Hogyan befolyásolja a kondenzátor a "mérőpont 2"-n az egész hálózatra mérhető jelterjedési időt (propagation time)?''' | |||
Lásd b) kérdés... | |||
== 7. Feladat == | |||
'''Rajzolja fel a földelt emitteres bipoláris tranzisztor 5 elemes helyettesítőképét! Adja meg a helyettesítőkép elemeit a tranzisztor fizikai paramétereivel!''' | |||
[[Laboratórium 1 - 2008 őszi ZH megoldások]] | |||
== 8. Feladat == | |||
'''Egy 4 bites egyenlőség komparátor egyik 4 bites bemenetére (A3-A0) egy 4 bites számláló van kapcsolva, a másik 4 bites bemenetére (B3-B0) 1000. A számláló 1MHz órajellel működik. A komparátor egyenlőség kimenetén hazárd jelenik meg, amelynek hossza 80...100ns. Röviden írja le, hogyan állapítaná meg logikai analizátor segítségével, hogy a számláló mely állapotátmeneténél van hazárd! A logikai analizátor mintavevő órajelének maximális frekvenciája 100MHz (T=10ns) és ennek 2-vel osztottjai állíthatók be.''' | |||
A mintavételi idő legyen kisebb mint 80ns az a lényeg, pl. 70ns jó lenne, de csak <math>10 \cdot n </math>, (ahol n=1,2,4,8,16...) állítható be, így 40ns. | A mintavételi idő legyen kisebb mint 80ns az a lényeg, pl. 70ns jó lenne, de csak <math>10 \cdot n </math>, (ahol n=1,2,4,8,16...) állítható be, így 40ns. A számláló mintavételi ideje 1 <math>\mu </math> s. A vizsgálathoz egy összetett triggerfeltétel kell, három egymásutáni állapot legyen: 010 és 0110. | ||
A számláló mintavételi ideje 1<math>\mu </math> s. | |||
A vizsgálathoz egy összetett triggerfeltétel kell, három egymásutáni állapot legyen: 010 és 0110. | |||
==== | == 9. Feladat == | ||
'''Ismertesse a párhuzamos port SPP és EPP módjai közötti fontosabb különbségeket! Melyik mód biztosít gyorsabb adatátviteli sebességet?''' | |||
* Az '''SPP''' módhoz '''egyetlen 8 bites kimeneti adatregiszter''' tartozik. Az '''EPP''' módhoz egy '''8 bites címregiszter és a lehetséges 256 egyedileg címezhető adat regiszter''' ből csak az első 4 címhez tartozik egy-egy írható/olvasható 8 bites adatregiszter. | * Az '''SPP''' módhoz '''egyetlen 8 bites kimeneti adatregiszter''' tartozik. Az '''EPP''' módhoz egy '''8 bites címregiszter és a lehetséges 256 egyedileg címezhető adat regiszter''' ből csak az első 4 címhez tartozik egy-egy írható/olvasható 8 bites adatregiszter. | ||
| 123. sor: | 131. sor: | ||
* '''EPP''' biztosít '''gyorsabb''' adatátvitelt. | * '''EPP''' biztosít '''gyorsabb''' adatátvitelt. | ||
== 10. Feladat == | |||
'''Adott egy speciális kódolású, 6-os számlálót megvalósító sorrendi hálózat, amelynek 4 kimenete van (Q0, Q1, Q2,Q3). A számláló ciklikusan a következő sorozatot adja ki: 1100, 0001, 0010, 0101, 0111, 0011, 1100, ... A hálózatról egy ''hagyományos oszcilloszkóp'' segítségével kell eldönteni, hogy megfelelően működik-e. Röviden írja le hogyan végezné el a mérést!''' | |||
Tudni kéne, hogy hány csatornás az oszcilloszkóp, mert pl. 4 csatornásra simán csak rátesszük az egyes kimeneteket 1-1 csatornára, és leellenőrizzük az értékeket. | |||
Ha 2 csatornás (mint ahogy a laborokban is), akkor 2 teljes ciklust ellenőrzünk végig. Elsőnél pl. a számláló alsó két bitjét tesszük az oszcilloszkóp bemeneteire és feljegyezzük az értékeket, a második ciklusban pedig a felső két bit kimenetét nézzük, így a második ciklus végére meglesznek az állapotkódok. | Ha 2 csatornás (mint ahogy a laborokban is), akkor 2 teljes ciklust ellenőrzünk végig. Elsőnél pl. a számláló alsó két bitjét tesszük az oszcilloszkóp bemeneteire és feljegyezzük az értékeket, a második ciklusban pedig a felső két bit kimenetét nézzük, így a második ciklus végére meglesznek az állapotkódok. | ||
[[Category:Villanyalap]] | [[Category:Villanyalap]] | ||
A lap 2013. február 8., 00:18-kori változata
1. Feladat
Egy kimeneti ellenállású generátor üresjárási feszültségének effektív értéke . A jelalak szinuszos, a jel frekvenciája . A generátor jelét egy hosszú, hullámimpedanciájú kábellel digitális feszültségmérőre vezetjük.
a) Rajzolja fel a mérési elrendezés modelljét! Mekkora a feszültségmérőre kerülő jel csúcstól csúcsig () értéke?
Ezt csak azért írom ide, mert meglehet oldani ezzel is, ezt vettük elektronika 2-ből.
Másképpen: kis vezetékeknél (a hullámhosszhoz képest) a bemeneti impedancia meg fog egyezni a vezeték végén lévő terheléssel (jelen esetben szakadás ,mert a volt mérőnek nagyon nagy a bementi impedanciája) illetve a mért feszültségek mindkét helyen közel (nagyon pici különbség) egyformák, így . Mivel ez effektív érték így az .
b) A jelet a fenti kábellel egy = bemeneti ellenállású eszközre vezetjük. Rajzolja fel ismét a mérési elrendezés modelljét és adja meg a bemenetre kerülő jel értékét!
Ugyanaz mint az első résznél, csak , tehát . Így az .
2. Feladat
hullámimpedanciájú hosszúságú kábelt hajtunk meg egy impedanciájú impulzusgenerátorral. Az elektromágneses hullám terjedési sebessége a kábelen előzetes mérések alapján . A kábelt szakadással "zárjuk le".
a) Mekkora lehet az impulzus maximális szélesség, hogy a kábel bemenetén ne lapolódjon át az eredeti és a reflektált impulzus?
Szakadással zárjuk le, , tehát 1 s telik el míg a jel eljut a bemenettől a lezárásig és onnan visszaér a bemenethez, tehát ez a maximális impulzusszélesség is.
b) Mekkora lehet az impulzus maximális szélessége akkor, ha rövidzárral zárjuk le a kábelt?
Rövidzárral zárjuk le,
A nem változik tehát a végeredmény ugyanaz, 1 s.
3. Feladat
Adott egy 10kHz frekvenciájú periodikus jel. Alapharmonikusának amplitúdója 2V, 10. felharmonikusának amplitúdója 10mV (a többi harmonikus elhanyagolható). A jelet a frekvenciatartományban FFT segítségével vizsgáljuk. A mintavételezés koherens.
a) Hány dB különbséget mérünk a két harmonikus amplitúdója között?
b) Hozzávetőlegesen hány dB lesz a különbség a két amplitúdó között, ha a jelet transzformáció előtt egy elsőfokú, 100Hz törésponti frekvenciájú aluláteresztő szűrőre vezetjük? Rajzolja be külön ábrába minőségileg helyesen a szűrő amplitúdókarakterisztikáját, valamint a jel spektrumát!
Az aluláteresztő szűrő a törésponti frekvenciája után 20dB-lel csökkenti az amplitúdót dekádonként.
| 100Hz | 0 dB | |
| 1kHz | -20 dB | |
| 10kHz | -40 dB | azaz az alapharmonikus amplitúdója -40dB-lel csökken ami két nagyságrend, tehát 0,02V az alapharmonikus |
| 100kHz | -60 dB | a 10. felharmonikus három nagyságrenddel csökken (-60dB), ami így V lesz |
Az arány:
Megjegyzés: Úgy is lehet gondolkozni, hogy az alapharmonikust 40dB-lel csökkenti, a felharmonikust 60dB-lel, tehát a kettő közötti különbség 20dB-lel nő, azaz a 46dB+20dB=66dB
4. Feladat
Adja meg egy légmagos és egy vasmagos tekercs modelljét! Ismertesse a modell paramétereit és azok fizikai hátterét!
| egyenáramon értelmezett induktivitás | |
| rézvezetőben örvényáram okozta veszteség | |
| menetek közötti kapacitás | |
| kapacitás dielektrikumában keletkező dielektromos veszteség | |
| soros rézellenállás |
Méréstechnika példatár: 7.17 feladat megoldása (172.oldal). Van egy párhuzamosan Rv és L és ezzel sorban egy Rs.
| vasveszteség | |
| induktivitás | |
| soros rézellenállás |
5. Feladat
Párhuzamos RC-tag in-circuit vizsgálatát végezzük. R = +-1%, C = 100nF +- 1%. Mekkora legyen a mérési frekvencia és az impedanciamérő mérési bizonytalansága?
6. Feladat
Adott az alábbi logikai hálózat. A hálózatot 10kHz-es négyszögjellel gerjesztjük.
a) Rajzolja fel a gerjesztőjel és a "mérőpont 1"-en mérhető jel hullámformáját!
Elvileg késleltet két inverterkésleltetési időnyit, a jelalakot a kondi megváltoztatja, mert a négyszögjel végtelen sok szinusz összege, és a kondenzátor végtelen frekvencián rövidzárként viselkedik, tehát egy "szűrő". Így a nagyfrekvenciás komponensek nem jelennek meg, nem lesz annyira négyszöges.
b) Hogyan befolyásolja a kondenzátor a "mérőpont 2"-n mérhető felfutási időt (rise time)?
Bár a kondi elrontja a négyszögjelet, emiatt a komparálási feszültséget később éri el a felfutó ill. lefutó él, így megnő a késleltetés. Ugyanakkor az inverterek a kondi után a négyszögjelet visszaállítják. A felfutási idő nem növekszik a mérőpont2-n (hála az invertereknek), csak késni fog, mert később éri el a komparálási feszültséget a jel.
c) Hogyan befolyásolja a kondenzátor a "mérőpont 2"-n az egész hálózatra mérhető jelterjedési időt (propagation time)?
Lásd b) kérdés...
7. Feladat
Rajzolja fel a földelt emitteres bipoláris tranzisztor 5 elemes helyettesítőképét! Adja meg a helyettesítőkép elemeit a tranzisztor fizikai paramétereivel!
Laboratórium 1 - 2008 őszi ZH megoldások
8. Feladat
Egy 4 bites egyenlőség komparátor egyik 4 bites bemenetére (A3-A0) egy 4 bites számláló van kapcsolva, a másik 4 bites bemenetére (B3-B0) 1000. A számláló 1MHz órajellel működik. A komparátor egyenlőség kimenetén hazárd jelenik meg, amelynek hossza 80...100ns. Röviden írja le, hogyan állapítaná meg logikai analizátor segítségével, hogy a számláló mely állapotátmeneténél van hazárd! A logikai analizátor mintavevő órajelének maximális frekvenciája 100MHz (T=10ns) és ennek 2-vel osztottjai állíthatók be.
A mintavételi idő legyen kisebb mint 80ns az a lényeg, pl. 70ns jó lenne, de csak , (ahol n=1,2,4,8,16...) állítható be, így 40ns. A számláló mintavételi ideje 1 s. A vizsgálathoz egy összetett triggerfeltétel kell, három egymásutáni állapot legyen: 010 és 0110.
9. Feladat
Ismertesse a párhuzamos port SPP és EPP módjai közötti fontosabb különbségeket! Melyik mód biztosít gyorsabb adatátviteli sebességet?
- Az SPP módhoz egyetlen 8 bites kimeneti adatregiszter tartozik. Az EPP módhoz egy 8 bites címregiszter és a lehetséges 256 egyedileg címezhető adat regiszter ből csak az első 4 címhez tartozik egy-egy írható/olvasható 8 bites adatregiszter.
- A párhuzamos port SPP üzemmódjában csak adatkivitel történik, nincs cím információ. Ekkor a kijelző formátuma ” dd”, ahol a ” ” két szóköz a felső két kijelző számjegy kikapcsolt állapotára utal, míg a ”dd” a kiküldött adat byte hexadecimális értéke az alsó két számjegyen. A párhuzamos port EPP üzemmódjában adat és cím kivitel ill. beolvasás is történhet. Ha az utolsó EPP ciklus cím átvitel volt, akkor a kijelző képe ”aa ”, ahol az ”aa” a kiküldött/beolvasott cím byte hexadecimális értéke a felső számjegyeken, míg a ” ” két szóköz az alsó két kijelző számjegy kikapcsolt állapotára utal.
- EPP biztosít gyorsabb adatátvitelt.
10. Feladat
Adott egy speciális kódolású, 6-os számlálót megvalósító sorrendi hálózat, amelynek 4 kimenete van (Q0, Q1, Q2,Q3). A számláló ciklikusan a következő sorozatot adja ki: 1100, 0001, 0010, 0101, 0111, 0011, 1100, ... A hálózatról egy hagyományos oszcilloszkóp segítségével kell eldönteni, hogy megfelelően működik-e. Röviden írja le hogyan végezné el a mérést!
Tudni kéne, hogy hány csatornás az oszcilloszkóp, mert pl. 4 csatornásra simán csak rátesszük az egyes kimeneteket 1-1 csatornára, és leellenőrizzük az értékeket.
Ha 2 csatornás (mint ahogy a laborokban is), akkor 2 teljes ciklust ellenőrzünk végig. Elsőnél pl. a számláló alsó két bitjét tesszük az oszcilloszkóp bemeneteire és feljegyezzük az értékeket, a második ciklusban pedig a felső két bit kimenetét nézzük, így a második ciklus végére meglesznek az állapotkódok.