„Jelek és jelfeldolgozás kvíz” változatai közötti eltérés

A VIK Wikiből

Névterek

Szócikk
Vitalap

Több

Több

Lapműveletek

Olvasás
Lapforrás
Laptörténet

@@ 1. sor: / 1. sor: @@
-{{Vissza | Menedzsment és vállalkozásgazdaságtan}}
+A csillaggal jelölt kérdések csak a vizsgán várhatóak.
+{{Vissza|Jelek és jelfeldolgozás}}
 {{Kvízoldal
-|cím=Jelek és jelfeldolgozás kvíz|pontozás=-}}A csillaggal jelölt kérdések csak a vizsgán várhatóak.
+| cím = Jelek és jelfeldolgozás kvíz
+| pontozás = +
+}}
+==Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza <math>h(t)=20\delta(t)-20\varepsilon(t)e^{-5t}</math>. Gerjesztés-válasz stabilis-e a rendszer?==
+{{kvízkérdés|típus=egy|válasz=3}}
+#Nem, mert az impulzusválaszban szerepel a <math>\delta(t)</math>.
+#Igen, mert az impulzusválasz belépő.
+#Igen, mert az impulzusválasz abszolút integrálható.
+#Nem, mert az impulzusválasz nem abszolút integrálható.
+#Igen, mert az impulzusválaszban szereplő <math>\delta(t)</math> és <math>\varepsilon(t)</math> együtthatója azonos nagyságú és ellentétes előjelű.
-==Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza <math>h(t)=20\delta(t)-20\epsilon(t)e^{-5t}</math>. Gerjesztés-válasz stabilis-e a rendszer?==
+== Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza <math>h(t)=20\delta(t)-20\varepsilon(t)e^{5t}</math>. Gerjesztés-válasz stabilis-e a rendszer? ==
-{{kvízkérdés|típus=egy|válasz=3|pontozás=+}}
+{{kvízkérdés|típus=egy|válasz=4}}
 #Nem, mert az impulzusválaszban szerepel a <math>\delta(t)</math>.
 #Igen, mert az impulzusválasz belépő.
 #Igen, mert az impulzusválasz abszolút integrálható.
 #Nem, mert az impulzusválasz nem abszolút integrálható.
-#Igen, mert az impulzusválaszban szereplő <math>\delta(t)</math> és <math>\epsilon(t)</math> együtthatója azonos nagyságú és ellentétes előjelű.
+#Igen, mert az impulzusválaszban szereplő <math>\delta(t)</math> és <math>\varepsilon(t)</math> együtthatója azonos nagyságú és ellentétes előjelű.
+==Egy folytonos idejű rendszer impulzusválasza <math>h(t)=4\varepsilon(t)e^{-2t}</math>. Adja meg a rendszer ugrásválaszát!==
+{{Kvízkérdés|típus=egy|válasz=4}}
+#<math>\varepsilon(t)(e^{-2t}-1)</math>
+#Nem létezik
+#<math>\varepsilon(t)e^{-2t}</math>
+#<math>-2\varepsilon(t)(e^{-2t}-1)</math>
+#<math>-4\varepsilon(t)(e^{-2t})</math>
+==Adott egy elsőrendű, folytonos idejű lineáris invariáns rendszer állapotváltozós leírásának normálalakja: <math>\begin{cases}
+x'(t)=2x(t)+3u(t) \\
+y(t)=-x(t) \\
+\end{cases}</math> Adja meg a rendszer állapotváltozóinak <math>x(t)</math> közelítő számításához szolgáló előrelépő Euler-séma formuláját!==
+{{Kvízkérdés|típus=egy|válasz=4}}
+#<math>x(t_k+h_k)\approx(1-h_k)x(t_k)-3h_ku(t_k)</math>
+#<math>x(t_k+h_k)\approx(1-2h_k)x(t_k)+3h_ku(t_k)</math>
+#<math>x(t_k+h_k)\approx(1-h_k)x(t_k)+3h_ku(t_k)</math>
+#<math>x(t_k+h_k)\approx(1+2h_k)x(t_k)+3h_ku(t_k)</math>
+==Adott egy elsőrendű, folytonos idejű lineáris invariáns rendszer állapotváltozós leírásának normálalakja: <math>\begin{cases}
+x'(t)=3x(t)+2u(t) \\
+y(t)=-x(t) \\
+\end{cases}</math> Adja meg a rendszer állapotváltozóinak <math>x(t)</math> közelítő számításához szolgáló előrelépő Euler-séma formuláját!==
+{{Kvízkérdés|típus=egy|válasz=2}}
+#<math>x(t_k+h_k)\approx(1+3h_k)x(t_k)+h_ku(t_k)</math>
+#<math>x(t_k+h_k)\approx(1+3h_k)x(t_k)+2h_ku(t_k)</math>
+#<math>x(t_k+h_k)\approx(1-h_k)x(t_k)-h_ku(t_k)</math>
+#<math>x(t_k+h_k)\approx(1+h_k)x(t_k)+h_ku(t_k)</math>
+==Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: <math>y(t)=5[u(t)]^2</math>. Jellemezze a rendszert!==
+{{Kvízkérdés|típus=több|válasz=1,2,4}}
+#invariáns
+#kauzális
+#lineáris
+#gerjesztés-válasz stabil
+==Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: <math>y(t)=5[u(t+3)]</math>. Jellemezze a rendszert!==
+{{Kvízkérdés|típus=több|válasz=1,3,4}}
+#invariáns
+#kauzális
+#lineáris
+#gerjesztés-válasz stabil
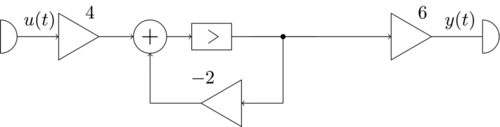
+==Az alábbi ábrán egy rendszert reprezentáló jelfolyamhálózat látható.==
+[[Fájl:Jelek_20240424_ZH_jelfolyamhálózat.png|keret|keretnélküli|500x500px]]
+Tekintsük folytonos idejűnek. Adja meg a rendszer állapotváltozós leírását normálalakban!
+{{Kvízkérdés|típus=egy|válasz=4}}
+#<math>\begin{cases}
+x'(t)=4x(t)+2u(t) \\
+y(t)=6x(t)
+\end{cases}</math>
+#<math>\begin{cases}
+x'(t)=-12x(t)+4u(t) \\
+y(t)=6x(t)
+\end{cases}</math>
+#<math>\begin{cases}
+x'(t)=2x(t)+4u(t) \\
+y(t)=6x(t)
+\end{cases}</math>
+#<math>\begin{cases}
+x'(t)=-2x(t)+4u(t) \\
+y(t)=6x(t)
+\end{cases}</math>
+Tekintsük diszkrét idejűnek. Adja meg a rendszer átviteli karakterisztikáját normálalakban!*
+{{Kvízkérdés|típus=egy|válasz=2}}
+# <math>H(e^{j\vartheta})=\frac{2+1e^{j\vartheta}}{3e^{j\vartheta}}</math>
+# <math>H(e^{j\vartheta})=\frac{12}{1+0,5e^{-j\vartheta}}</math>
+# <math>H(e^{j\vartheta})=\frac{12}{1-0,5e^{-j\vartheta}}</math>
+# <math>H(e^{j\vartheta})=\frac{6}{1-0,5e^{-j\vartheta}}</math>
+# <math>H(e^{j\vartheta})=\frac{6}{1+0,5e^{-j\vartheta}}</math>
+# <math>H(e^{j\vartheta})=\frac{2+1e^{j\vartheta}}{6e^{j\vartheta}}</math>
+==Egy diszkrét idejű rendszer ugrásválasza <math>g[k]=\varepsilon[k]2^k</math>. Adja meg a rendszer <math>h[k]</math> impulzusválaszát!==
+{{Kvízkérdés|típus=egy|válasz=3}}
+#<math>\frac{1}{2}\delta[k]</math>
+#<math>\frac{1}{2}\varepsilon[k]2^k</math>
+#<math>\frac{1}{2}\delta[k]+\frac{1}{2}\varepsilon[k]2^k</math>
+#Nem létezik
+#<math>\delta[k]+\varepsilon[k]2^k</math>
+==Egy diszkrét idejű rendszer rendszeregyenlete <math>y[k]+5y[k-1]=u[k]-2u[k-1]</math>. Adja meg a rendszer átviteli karakterisztikáját!==
+{{Kvízkérdés|típus=egy|válasz=3}}
+#<math>H(e^{j\vartheta})=\frac{-1+2e^{-j\vartheta}}{1+5e^{-j\vartheta}}</math>
+#Nem létezik
+#<math>H(e^{j\vartheta})=\frac{1-2e^{-j\vartheta}}{1+5e^{-j\vartheta}}</math>
+#<math>H(e^{j\vartheta})=\frac{-1+2e^{-j\vartheta}}{1-5e^{-j\vartheta}}</math>
+#<math>H(e^{j\vartheta})=\frac{1-2e^{-j\vartheta}}{1-5e^{-j\vartheta}}</math>
+==Egy diszkrét idejű jel időfüggvénye a <math>x[k]=\cos[0,4\pi k+4]</math>. Állapítsa meg a jel <math>L</math> periódushosszát!==
+A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.
+{{Kvízkérdés|típus=egy|válasz=3}}
+#3
+#4
+#5
+#6
+==Egy diszkrét idejű jel időfüggvénye a <math>x[k]=\cos[0,75\pi k+4]</math>. Állapítsa meg a jel <math>L</math> periódushosszát!==
+A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.
+{{Kvízkérdés|típus=egy|válasz=2}}
+#3
+#4
+#5
+#6
+==Egy diszkrét idejű, lineáris, invariáns rendszer ugrásválasza <math>y[k]=5\cdot0,8^k\varepsilon[k]</math>. Adja meg a rendszer válaszát az <math>u[k]=2\cdot\varepsilon[k+3]</math> gerjesztésre!==
+{{Kvízkérdés|típus=egy|válasz=3}}
+#<math>5\cdot0,8^{k+3}\varepsilon[k+3]</math>
+#Az <math>u[k]</math> nem belépő, ezért nem létezik
+#<math>10\cdot0,8^{k+3}\varepsilon[k+3]</math>
+#<math>10\cdot0,8^{k-3}\varepsilon[k-3]</math>
+#<math>5\cdot0,8^{k-3}\varepsilon[k]</math>
+==Egy diszkrét idejű jel időfüggvénye <math>x[k]=2\cos[0,25\pi k-1,25]</math>. Adja meg a jel fazorát (komplex csúcsértékét)!==
+{{Kvízkérdés|típus=egy|válasz=4}}
+#<math>\bar X=2e^{j0,25}</math>
+#<math>\bar X=2e^{j1,25}</math>
+#<math>\bar X=2e^{-j0,25}</math>
+#<math>\bar X=2e^{-j1,25}</math>
+==Egy diszkrét idejű jel időfüggvénye <math>x[k]=5\cos[0,5\pi k-0,5]</math>. Adja meg a jel fazorát (komplex csúcsértékét)!==
+{{Kvízkérdés|típus=egy|válasz=3}}
+#<math>\bar X=5e^{j0,5}</math>
+#<math>\bar X=0,5e^{j0,5}</math>
+#<math>\bar X=5e^{-j0,5}</math>
+#<math>\bar X=0,5e^{-j0,05}</math>
+== Egy diszkrét idejű rendszer gerjesztésének fazora a <math>\vartheta=\frac{\pi}{4}</math> körfrekvencián <math>\bar U=5e^{j0,4}</math>. A rendszer átviteli tényezője ugyanezen a körfrekvencián <math>\bar H=2e^{-j1,2}</math>. Határozza meg a rendszer válaszának időfüggvényét!* ==
+{{Kvízkérdés|típus=egy|válasz=2}}
+# <math>y[k]=10\cos(\frac{\pi}{4}k+0,8)</math>
+# <math>y[k]=10\cos(\frac{\pi}{4}k-0,8)</math>
+# <math>y[k]=10\cos(0,8k+\frac{\pi}{4})</math>
+# <math>y[k]=5\cos(\frac{\pi}{4}k+0,4)</math>
+# <math>y[k]=5\cos(\frac{\pi}{4}k+1,4)</math>
+# <math>y[k]=5\cos(0,8k+\frac{\pi}{4})</math>
+== Egy diszkrét idejű jel spektruma a <math>\vartheta=[0,\pi]</math> intervallumon <math>X(e^{j\vartheta})=\pi-\vartheta</math>. Határozza meg a jel sávszélességét, ha <math>\sigma=0,1</math>.* ==
+{{Kvízkérdés|típus=egy|válasz=5}}
+# <math>0,9</math>
+# <math>0,1\pi</math>
+# <math>0,1</math>
+# <math>0,81\pi</math>
+# <math>0,9\pi</math>
+# <math>0,01\pi</math>
+== Mely tulajdonság(ok) jellemző(ek) egy FIR típusú diszkrét idejű rendszerre?* ==
+{{Kvízkérdés|típus=több|válasz=3}}
+# Mindig konstans az amplitúdókarakterisztikája
+# Impulzusválasza mindig monoton csökkenő
+# Mindig gerjesztés-válasz stabil
+# Mindig lineáris az amplitúdókarakterisztikája
+== Egy periodikus diszkrét idejű jel periódushossza <math>L=4</math>. Egy periódusának mintái: <math>x[0]=-1,\ x[1]=1,\ x[2]=1,\ x[3]=1</math>. Adja meg a jel nulladik komplex Fourier-együtthatójának értékét, <math>X^C_0</math>-t, két tizedesjegy pontossággal!* ==
+A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.
+{{Kvízkérdés|típus=egy|válasz=2}}
+# 0,25
+# 0,5
+# 1
+# 1,25
+# 2,5
+== Mely tulajdonság(ok) jellemzik a torzításmentes jelátvitelt megvalósító rendszert?* ==
+{{Kvízkérdés|típus=több|válasz=1,4,5}}
+# Konstans futásidő-karakterisztika
+# Lineáris amplitúdókarakterisztika
+# Lineáris futásidő-karakterisztika
+# Konstans amplitúdókarakterisztika
+# Lineáris fáziskarakterisztika
+== Egy <math>L=4</math> periódusidejű jel komplex Fourier-együtthatói: <math>X^C_0=1,\ X^C_1=2e^{j0,2},\ X^C_2=0</math>. Adja meg a jel ''mérnöki valós alakjának'' megfelelő időfüggvényét!* ==
+{{Kvízkérdés|típus=egy|válasz=4}}
+# <math>x[k]=1+2\cos(\frac{\pi}{2}k+0,2)</math>
+# <math>x[k]=1+0,2\cos(\frac{\pi}{2}k+2)</math>
+# <math>x[k]=2+4\cos(\frac{\pi}{2}k+0,2)</math>
+# <math>x[k]=1+4\cos(\frac{\pi}{2}k+0,2)</math>
+# <math>x[k]=2+4\cos(\frac{\pi}{2}k+0,4)</math>
+== Egy folytonos idejű jel mintavételezése során a mintavételi körfrekvencia 8 krad/s. Határozza meg a folytonos idejű jel maximális sávszélességét, amelynek ezzel a mintavételezéssel az időfüggvénye helyreállítható (rekonstruálható)!* ==
+A választ 1 tizedesjegy pontossággal, krad/s-ban adja meg! ''A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.''
+{{Kvízkérdés|típus=egy|válasz=3}}
+# 0.5
+# 2
+# 4
+# 8
+# 16
+== Egy diszkrét idejű rendszer átviteli karakterisztikája <math>H(e^{j\vartheta})=\frac{e^{-j\vartheta}+e^{-j2\vartheta}}{1+e^{-j\vartheta}+e^{-j2\vartheta}}</math>. Adja meg a rendszer átviteli tényezőjét a <math>\vartheta=\frac{\pi}{2}</math> körfrekvencián!* ==
+{{Kvízkérdés|típus=egy|válasz=3}}
+# <math>\sqrt2e^{j\frac{\pi}{4}}</math>
+# <math>2e^{j\frac{\pi}{4}}</math>
+# <math>\sqrt2e^{-j\frac{\pi}{4}}</math>
+# <math>2e^{-j\frac{\pi}{4}}</math>
+# <math>4e^{j\frac{\pi}{4}}</math>
+# <math>4e^{-j\frac{\pi}{4}}</math>
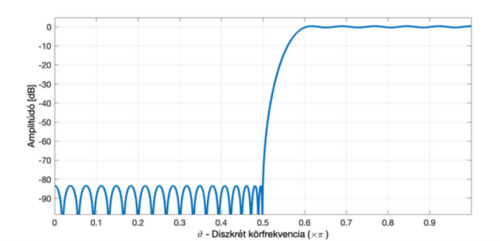
+== Egy diszkrét idejű rendszer amplitúdókarakterisztikája az alábbi ábrán látható. Határozza meg, hogy milyen típusú szűrőt valósít meg a rendszer a toleranciaséma alapján, ha az áteresztő és a zárósáv között legalább 10 dB eltérésnek kell lennie!* ==
+[[Fájl:Jelek vizsga amplitúdókarakterisztika.png|keret|keretnélküli|500x500px]]
+{{Kvízkérdés|típus=egy|válasz=5}}
+# Sávzáró
+# Minimálfázisú
+# Sáváteresztő
+# Mindent áteresztő
+# Felüláteresztő
+# Aluláteresztő

A lap jelenlegi, 2024. június 9., 04:35-kori változata

A csillaggal jelölt kérdések csak a vizsgán várhatóak.

← Vissza az előző oldalra – Jelek és jelfeldolgozás

Jelek és jelfeldolgozás kvíz

Statisztika

Kvízek használata, importálása, fejlesztése.
Átlagteljesítmény
Eddigi kérdések	0
Kapott pontok	0
Alapbeállított pontozás	(+)

Beállítások
Minden kérdés látszik
Véletlenszerű sorrend

Adott egy elsőrendű, folytonos idejű lineáris invariáns rendszer állapotváltozós leírásának normálalakja: ${\begin{cases} x^{'} (t) = 2 x (t) + 3 u (t) \\ y (t) = - x (t) \end{cases}$ Adja meg a rendszer állapotváltozóinak $x (t)$ közelítő számításához szolgáló előrelépő Euler-séma formuláját!

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

$x (t_{k} + h_{k}) \approx (1 - h_{k}) x (t_{k}) - 3 h_{k} u (t_{k})$
$x (t_{k} + h_{k}) \approx (1 - 2 h_{k}) x (t_{k}) + 3 h_{k} u (t_{k})$
$x (t_{k} + h_{k}) \approx (1 - h_{k}) x (t_{k}) + 3 h_{k} u (t_{k})$
$x (t_{k} + h_{k}) \approx (1 + 2 h_{k}) x (t_{k}) + 3 h_{k} u (t_{k})$

Egy diszkrét idejű jel időfüggvénye $x [k] = 2 \cos [0, 25 π k - 1, 25]$ . Adja meg a jel fazorát (komplex csúcsértékét)!

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

$\bar{X} = 2 e^{j 0, 25}$
$\bar{X} = 2 e^{j 1, 25}$
$\bar{X} = 2 e^{- j 0, 25}$
$\bar{X} = 2 e^{- j 1, 25}$

Egy diszkrét idejű, lineáris, invariáns rendszer ugrásválasza $y [k] = 5 \cdot 0, 8^{k} ε [k]$ . Adja meg a rendszer válaszát az $u [k] = 2 \cdot ε [k + 3]$ gerjesztésre!

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

$5 \cdot 0, 8^{k + 3} ε [k + 3]$
Az $u [k]$ nem belépő, ezért nem létezik
$10 \cdot 0, 8^{k + 3} ε [k + 3]$
$10 \cdot 0, 8^{k - 3} ε [k - 3]$
$5 \cdot 0, 8^{k - 3} ε [k]$

Egy periodikus diszkrét idejű jel periódushossza $L = 4$ . Egy periódusának mintái: $x [0] = - 1, x [1] = 1, x [2] = 1, x [3] = 1$ . Adja meg a jel nulladik komplex Fourier-együtthatójának értékét, $X_{0}^{C}$ -t, két tizedesjegy pontossággal!*

A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

0,25
0,5
1
1,25
2,5

Egy diszkrét idejű jel spektruma a $ϑ = [0, π]$ intervallumon $X (e^{j ϑ}) = π - ϑ$ . Határozza meg a jel sávszélességét, ha $σ = 0, 1$ .*

Típus: egy. Válasz: 5. Pontozás: nincs megadva.

$0, 9$
$0, 1 π$
$0, 1$
$0, 81 π$
$0, 9 π$
$0, 01 π$

Egy diszkrét idejű rendszer ugrásválasza $g [k] = ε [k] 2^{k}$ . Adja meg a rendszer $h [k]$ impulzusválaszát!

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

$\frac{1}{2} δ [k]$
$\frac{1}{2} ε [k] 2^{k}$
$\frac{1}{2} δ [k] + \frac{1}{2} ε [k] 2^{k}$
Nem létezik
$δ [k] + ε [k] 2^{k}$

Egy diszkrét idejű rendszer gerjesztésének fazora a $ϑ = \frac{π}{4}$ körfrekvencián $\bar{U} = 5 e^{j 0, 4}$ . A rendszer átviteli tényezője ugyanezen a körfrekvencián $\bar{H} = 2 e^{- j 1, 2}$ . Határozza meg a rendszer válaszának időfüggvényét!*

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

$y [k] = 10 \cos (\frac{π}{4} k + 0, 8)$
$y [k] = 10 \cos (\frac{π}{4} k - 0, 8)$
$y [k] = 10 \cos (0, 8 k + \frac{π}{4})$
$y [k] = 5 \cos (\frac{π}{4} k + 0, 4)$
$y [k] = 5 \cos (\frac{π}{4} k + 1, 4)$
$y [k] = 5 \cos (0, 8 k + \frac{π}{4})$

Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza $h (t) = 20 δ (t) - 20 ε (t) e^{5 t}$ . Gerjesztés-válasz stabilis-e a rendszer?

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

Nem, mert az impulzusválaszban szerepel a $δ (t)$ .
Igen, mert az impulzusválasz belépő.
Igen, mert az impulzusválasz abszolút integrálható.
Nem, mert az impulzusválasz nem abszolút integrálható.
Igen, mert az impulzusválaszban szereplő $δ (t)$ és $ε (t)$ együtthatója azonos nagyságú és ellentétes előjelű.

Egy diszkrét idejű jel időfüggvénye a $x [k] = \cos [0, 75 π k + 4]$ . Állapítsa meg a jel $L$ periódushosszát!

A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

Az alábbi ábrán egy rendszert reprezentáló jelfolyamhálózat látható.

Tekintsük folytonos idejűnek. Adja meg a rendszer állapotváltozós leírását normálalakban!

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

${\begin{cases} x^{'} (t) = 4 x (t) + 2 u (t) \\ y (t) = 6 x (t) \end{cases}$
${\begin{cases} x^{'} (t) = - 12 x (t) + 4 u (t) \\ y (t) = 6 x (t) \end{cases}$
${\begin{cases} x^{'} (t) = 2 x (t) + 4 u (t) \\ y (t) = 6 x (t) \end{cases}$
${\begin{cases} x^{'} (t) = - 2 x (t) + 4 u (t) \\ y (t) = 6 x (t) \end{cases}$

Tekintsük diszkrét idejűnek. Adja meg a rendszer átviteli karakterisztikáját normálalakban!*

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

$H (e^{j ϑ}) = \frac{2 + 1 e^{j ϑ}}{3 e^{j ϑ}}$
$H (e^{j ϑ}) = \frac{12}{1 + 0, 5 e^{- j ϑ}}$
$H (e^{j ϑ}) = \frac{12}{1 - 0, 5 e^{- j ϑ}}$
$H (e^{j ϑ}) = \frac{6}{1 - 0, 5 e^{- j ϑ}}$
$H (e^{j ϑ}) = \frac{6}{1 + 0, 5 e^{- j ϑ}}$
$H (e^{j ϑ}) = \frac{2 + 1 e^{j ϑ}}{6 e^{j ϑ}}$

Mely tulajdonság(ok) jellemző(ek) egy FIR típusú diszkrét idejű rendszerre?*

Típus: több. Válasz: 3. Pontozás: nincs megadva.

Mindig konstans az amplitúdókarakterisztikája
Impulzusválasza mindig monoton csökkenő
Mindig gerjesztés-válasz stabil
Mindig lineáris az amplitúdókarakterisztikája

Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza $h (t) = 20 δ (t) - 20 ε (t) e^{- 5 t}$ . Gerjesztés-válasz stabilis-e a rendszer?

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

Nem, mert az impulzusválaszban szerepel a $δ (t)$ .
Igen, mert az impulzusválasz belépő.
Igen, mert az impulzusválasz abszolút integrálható.
Nem, mert az impulzusválasz nem abszolút integrálható.
Igen, mert az impulzusválaszban szereplő $δ (t)$ és $ε (t)$ együtthatója azonos nagyságú és ellentétes előjelű.

Egy diszkrét idejű rendszer amplitúdókarakterisztikája az alábbi ábrán látható. Határozza meg, hogy milyen típusú szűrőt valósít meg a rendszer a toleranciaséma alapján, ha az áteresztő és a zárósáv között legalább 10 dB eltérésnek kell lennie!*

Típus: egy. Válasz: 5. Pontozás: nincs megadva.

Sávzáró
Minimálfázisú
Sáváteresztő
Mindent áteresztő
Felüláteresztő
Aluláteresztő

Egy $L = 4$ periódusidejű jel komplex Fourier-együtthatói: $X_{0}^{C} = 1, X_{1}^{C} = 2 e^{j 0, 2}, X_{2}^{C} = 0$ . Adja meg a jel mérnöki valós alakjának megfelelő időfüggvényét!*

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

$x [k] = 1 + 2 \cos (\frac{π}{2} k + 0, 2)$
$x [k] = 1 + 0, 2 \cos (\frac{π}{2} k + 2)$
$x [k] = 2 + 4 \cos (\frac{π}{2} k + 0, 2)$
$x [k] = 1 + 4 \cos (\frac{π}{2} k + 0, 2)$
$x [k] = 2 + 4 \cos (\frac{π}{2} k + 0, 4)$

Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: $y (t) = 5 [u (t + 3)]$ . Jellemezze a rendszert!

Típus: több. Válasz: 1,3,4. Pontozás: nincs megadva.

invariáns
kauzális
lineáris
gerjesztés-válasz stabil

Egy diszkrét idejű jel időfüggvénye a $x [k] = \cos [0, 4 π k + 4]$ . Állapítsa meg a jel $L$ periódushosszát!

A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

Egy diszkrét idejű jel időfüggvénye $x [k] = 5 \cos [0, 5 π k - 0, 5]$ . Adja meg a jel fazorát (komplex csúcsértékét)!

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

$\bar{X} = 5 e^{j 0, 5}$
$\bar{X} = 0, 5 e^{j 0, 5}$
$\bar{X} = 5 e^{- j 0, 5}$
$\bar{X} = 0, 5 e^{- j 0, 05}$

Egy diszkrét idejű rendszer rendszeregyenlete $y [k] + 5 y [k - 1] = u [k] - 2 u [k - 1]$ . Adja meg a rendszer átviteli karakterisztikáját!

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

$H (e^{j ϑ}) = \frac{- 1 + 2 e^{- j ϑ}}{1 + 5 e^{- j ϑ}}$
Nem létezik
$H (e^{j ϑ}) = \frac{1 - 2 e^{- j ϑ}}{1 + 5 e^{- j ϑ}}$
$H (e^{j ϑ}) = \frac{- 1 + 2 e^{- j ϑ}}{1 - 5 e^{- j ϑ}}$
$H (e^{j ϑ}) = \frac{1 - 2 e^{- j ϑ}}{1 - 5 e^{- j ϑ}}$

Adott egy elsőrendű, folytonos idejű lineáris invariáns rendszer állapotváltozós leírásának normálalakja: ${\begin{cases} x^{'} (t) = 3 x (t) + 2 u (t) \\ y (t) = - x (t) \end{cases}$ Adja meg a rendszer állapotváltozóinak $x (t)$ közelítő számításához szolgáló előrelépő Euler-séma formuláját!

Típus: egy. Válasz: 2. Pontozás: nincs megadva.

$x (t_{k} + h_{k}) \approx (1 + 3 h_{k}) x (t_{k}) + h_{k} u (t_{k})$
$x (t_{k} + h_{k}) \approx (1 + 3 h_{k}) x (t_{k}) + 2 h_{k} u (t_{k})$
$x (t_{k} + h_{k}) \approx (1 - h_{k}) x (t_{k}) - h_{k} u (t_{k})$
$x (t_{k} + h_{k}) \approx (1 + h_{k}) x (t_{k}) + h_{k} u (t_{k})$

Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: $y (t) = 5 [u (t)]^{2}$ . Jellemezze a rendszert!

Típus: több. Válasz: 1,2,4. Pontozás: nincs megadva.

invariáns
kauzális
lineáris
gerjesztés-válasz stabil

Egy folytonos idejű rendszer impulzusválasza $h (t) = 4 ε (t) e^{- 2 t}$ . Adja meg a rendszer ugrásválaszát!

Típus: egy. Válasz: 4. Pontozás: nincs megadva.

$ε (t) (e^{- 2 t} - 1)$
Nem létezik
$ε (t) e^{- 2 t}$
$- 2 ε (t) (e^{- 2 t} - 1)$
$- 4 ε (t) (e^{- 2 t})$

Egy diszkrét idejű rendszer átviteli karakterisztikája $H (e^{j ϑ}) = \frac{e^{- j ϑ} + e^{- j 2 ϑ}}{1 + e^{- j ϑ} + e^{- j 2 ϑ}}$ . Adja meg a rendszer átviteli tényezőjét a $ϑ = \frac{π}{2}$ körfrekvencián!*

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

$\sqrt{2} e^{j \frac{π}{4}}$
$2 e^{j \frac{π}{4}}$
$\sqrt{2} e^{- j \frac{π}{4}}$
$2 e^{- j \frac{π}{4}}$
$4 e^{j \frac{π}{4}}$
$4 e^{- j \frac{π}{4}}$

Mely tulajdonság(ok) jellemzik a torzításmentes jelátvitelt megvalósító rendszert?*

Típus: több. Válasz: 1,4,5. Pontozás: nincs megadva.

Konstans futásidő-karakterisztika
Lineáris amplitúdókarakterisztika
Lineáris futásidő-karakterisztika
Konstans amplitúdókarakterisztika
Lineáris fáziskarakterisztika

Egy folytonos idejű jel mintavételezése során a mintavételi körfrekvencia 8 krad/s. Határozza meg a folytonos idejű jel maximális sávszélességét, amelynek ezzel a mintavételezéssel az időfüggvénye helyreállítható (rekonstruálható)!*

A választ 1 tizedesjegy pontossággal, krad/s-ban adja meg! A vizsgán nincsenek válaszlehetőségek, csak egy szövegmező.

Típus: egy. Válasz: 3. Pontozás: nincs megadva.

A lap eredeti címe: „https://vik.wiki/index.php?title=Jelek_és_jelfeldolgozás_kvíz&oldid=205637”

Bejelentkezés

Keresés

„Jelek és jelfeldolgozás kvíz” változatai közötti eltérés

Névterek

Több

Lapműveletek

A lap jelenlegi, 2024. június 9., 04:35-kori változata

Egy diszkrét idejű jel időfüggvénye $x [k] = 2 \cos [0, 25 π k - 1, 25]$ . Adja meg a jel fazorát (komplex csúcsértékét)!

Egy diszkrét idejű, lineáris, invariáns rendszer ugrásválasza $y [k] = 5 \cdot 0, 8^{k} ε [k]$ . Adja meg a rendszer válaszát az $u [k] = 2 \cdot ε [k + 3]$ gerjesztésre!

Egy periodikus diszkrét idejű jel periódushossza $L = 4$ . Egy periódusának mintái: $x [0] = - 1, x [1] = 1, x [2] = 1, x [3] = 1$ . Adja meg a jel nulladik komplex Fourier-együtthatójának értékét, $X_{0}^{C}$ -t, két tizedesjegy pontossággal!*

Egy diszkrét idejű jel spektruma a $ϑ = [0, π]$ intervallumon $X (e^{j ϑ}) = π - ϑ$ . Határozza meg a jel sávszélességét, ha $σ = 0, 1$ .*

Egy diszkrét idejű rendszer ugrásválasza $g [k] = ε [k] 2^{k}$ . Adja meg a rendszer $h [k]$ impulzusválaszát!

Egy diszkrét idejű rendszer gerjesztésének fazora a $ϑ = \frac{π}{4}$ körfrekvencián $\bar{U} = 5 e^{j 0, 4}$ . A rendszer átviteli tényezője ugyanezen a körfrekvencián $\bar{H} = 2 e^{- j 1, 2}$ . Határozza meg a rendszer válaszának időfüggvényét!*

Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza $h (t) = 20 δ (t) - 20 ε (t) e^{5 t}$ . Gerjesztés-válasz stabilis-e a rendszer?

Egy diszkrét idejű jel időfüggvénye a $x [k] = \cos [0, 75 π k + 4]$ . Állapítsa meg a jel $L$ periódushosszát!

Az alábbi ábrán egy rendszert reprezentáló jelfolyamhálózat látható.

Mely tulajdonság(ok) jellemző(ek) egy FIR típusú diszkrét idejű rendszerre?*

Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza $h (t) = 20 δ (t) - 20 ε (t) e^{- 5 t}$ . Gerjesztés-válasz stabilis-e a rendszer?

Egy diszkrét idejű rendszer amplitúdókarakterisztikája az alábbi ábrán látható. Határozza meg, hogy milyen típusú szűrőt valósít meg a rendszer a toleranciaséma alapján, ha az áteresztő és a zárósáv között legalább 10 dB eltérésnek kell lennie!*

Egy $L = 4$ periódusidejű jel komplex Fourier-együtthatói: $X_{0}^{C} = 1, X_{1}^{C} = 2 e^{j 0, 2}, X_{2}^{C} = 0$ . Adja meg a jel mérnöki valós alakjának megfelelő időfüggvényét!*

Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: $y (t) = 5 [u (t + 3)]$ . Jellemezze a rendszert!

Egy diszkrét idejű jel időfüggvénye a $x [k] = \cos [0, 4 π k + 4]$ . Állapítsa meg a jel $L$ periódushosszát!

Egy diszkrét idejű jel időfüggvénye $x [k] = 5 \cos [0, 5 π k - 0, 5]$ . Adja meg a jel fazorát (komplex csúcsértékét)!

Egy diszkrét idejű rendszer rendszeregyenlete $y [k] + 5 y [k - 1] = u [k] - 2 u [k - 1]$ . Adja meg a rendszer átviteli karakterisztikáját!

Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: $y (t) = 5 [u (t)]^{2}$ . Jellemezze a rendszert!

Egy folytonos idejű rendszer impulzusválasza $h (t) = 4 ε (t) e^{- 2 t}$ . Adja meg a rendszer ugrásválaszát!

Egy diszkrét idejű rendszer átviteli karakterisztikája $H (e^{j ϑ}) = \frac{e^{- j ϑ} + e^{- j 2 ϑ}}{1 + e^{- j ϑ} + e^{- j 2 ϑ}}$ . Adja meg a rendszer átviteli tényezőjét a $ϑ = \frac{π}{2}$ körfrekvencián!*

Mely tulajdonság(ok) jellemzik a torzításmentes jelátvitelt megvalósító rendszert?*

Egy folytonos idejű jel mintavételezése során a mintavételi körfrekvencia 8 krad/s. Határozza meg a folytonos idejű jel maximális sávszélességét, amelynek ezzel a mintavételezéssel az időfüggvénye helyreállítható (rekonstruálható)!*

Navigáció

Navigáció

Egyetem

Wikieszközök

Wikieszközök

Bejelentkezés

Keresés

„Jelek és jelfeldolgozás kvíz” változatai közötti eltérés

A lap jelenlegi, 2024. június 9., 04:35-kori változata

Adott egy elsőrendű, folytonos idejű lineáris invariáns rendszer állapotváltozós leírásának normálalakja: {x′(t)=2x(t)+3u(t)y(t)=−x(t) Adja meg a rendszer állapotváltozóinak x(t) közelítő számításához szolgáló előrelépő Euler-séma formuláját!

Egy diszkrét idejű jel időfüggvénye x[k]=2cos⁡[0,25πk−1,25]. Adja meg a jel fazorát (komplex csúcsértékét)!

Egy diszkrét idejű, lineáris, invariáns rendszer ugrásválasza y[k]=5⋅0,8kε[k]. Adja meg a rendszer válaszát az u[k]=2⋅ε[k+3] gerjesztésre!

Egy periodikus diszkrét idejű jel periódushossza L=4. Egy periódusának mintái: x[0]=−1,x[1]=1,x[2]=1,x[3]=1. Adja meg a jel nulladik komplex Fourier-együtthatójának értékét, X0C-t, két tizedesjegy pontossággal!*

Egy diszkrét idejű jel spektruma a ϑ=[0,π] intervallumon X(ejϑ)=π−ϑ. Határozza meg a jel sávszélességét, ha σ=0,1.*

Egy diszkrét idejű rendszer ugrásválasza g[k]=ε[k]2k. Adja meg a rendszer h[k] impulzusválaszát!

Egy diszkrét idejű rendszer gerjesztésének fazora a ϑ=π4 körfrekvencián U¯=5ej0,4. A rendszer átviteli tényezője ugyanezen a körfrekvencián H¯=2e−j1,2. Határozza meg a rendszer válaszának időfüggvényét!*

Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza h(t)=20δ(t)−20ε(t)e5t. Gerjesztés-válasz stabilis-e a rendszer?

Egy diszkrét idejű jel időfüggvénye a x[k]=cos⁡[0,75πk+4]. Állapítsa meg a jel L periódushosszát!

Az alábbi ábrán egy rendszert reprezentáló jelfolyamhálózat látható.

Mely tulajdonság(ok) jellemző(ek) egy FIR típusú diszkrét idejű rendszerre?*

Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza h(t)=20δ(t)−20ε(t)e−5t. Gerjesztés-válasz stabilis-e a rendszer?

Egy diszkrét idejű rendszer amplitúdókarakterisztikája az alábbi ábrán látható. Határozza meg, hogy milyen típusú szűrőt valósít meg a rendszer a toleranciaséma alapján, ha az áteresztő és a zárósáv között legalább 10 dB eltérésnek kell lennie!*

Egy L=4 periódusidejű jel komplex Fourier-együtthatói: X0C=1,X1C=2ej0,2,X2C=0. Adja meg a jel mérnöki valós alakjának megfelelő időfüggvényét!*

Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: y(t)=5[u(t+3)]. Jellemezze a rendszert!

Egy diszkrét idejű jel időfüggvénye a x[k]=cos⁡[0,4πk+4]. Állapítsa meg a jel L periódushosszát!

Egy diszkrét idejű jel időfüggvénye x[k]=5cos⁡[0,5πk−0,5]. Adja meg a jel fazorát (komplex csúcsértékét)!

Egy diszkrét idejű rendszer rendszeregyenlete y[k]+5y[k−1]=u[k]−2u[k−1]. Adja meg a rendszer átviteli karakterisztikáját!

Adott egy elsőrendű, folytonos idejű lineáris invariáns rendszer állapotváltozós leírásának normálalakja: {x′(t)=3x(t)+2u(t)y(t)=−x(t) Adja meg a rendszer állapotváltozóinak x(t) közelítő számításához szolgáló előrelépő Euler-séma formuláját!

Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: y(t)=5[u(t)]2. Jellemezze a rendszert!

Egy folytonos idejű rendszer impulzusválasza h(t)=4ε(t)e−2t. Adja meg a rendszer ugrásválaszát!

Egy diszkrét idejű rendszer átviteli karakterisztikája H(ejϑ)=e−jϑ+e−j2ϑ1+e−jϑ+e−j2ϑ. Adja meg a rendszer átviteli tényezőjét a ϑ=π2 körfrekvencián!*

Mely tulajdonság(ok) jellemzik a torzításmentes jelátvitelt megvalósító rendszert?*

Egy folytonos idejű jel mintavételezése során a mintavételi körfrekvencia 8 krad/s. Határozza meg a folytonos idejű jel maximális sávszélességét, amelynek ezzel a mintavételezéssel az időfüggvénye helyreállítható (rekonstruálható)!*

Navigáció

Wikieszközök

Eszközök

Kategóriák

Egy diszkrét idejű jel időfüggvénye $x [k] = 2 \cos [0, 25 π k - 1, 25]$ . Adja meg a jel fazorát (komplex csúcsértékét)!

Egy diszkrét idejű, lineáris, invariáns rendszer ugrásválasza $y [k] = 5 \cdot 0, 8^{k} ε [k]$ . Adja meg a rendszer válaszát az $u [k] = 2 \cdot ε [k + 3]$ gerjesztésre!

Egy periodikus diszkrét idejű jel periódushossza $L = 4$ . Egy periódusának mintái: $x [0] = - 1, x [1] = 1, x [2] = 1, x [3] = 1$ . Adja meg a jel nulladik komplex Fourier-együtthatójának értékét, $X_{0}^{C}$ -t, két tizedesjegy pontossággal!*

Egy diszkrét idejű jel spektruma a $ϑ = [0, π]$ intervallumon $X (e^{j ϑ}) = π - ϑ$ . Határozza meg a jel sávszélességét, ha $σ = 0, 1$ .*

Egy diszkrét idejű rendszer ugrásválasza $g [k] = ε [k] 2^{k}$ . Adja meg a rendszer $h [k]$ impulzusválaszát!

Egy diszkrét idejű rendszer gerjesztésének fazora a $ϑ = \frac{π}{4}$ körfrekvencián $\bar{U} = 5 e^{j 0, 4}$ . A rendszer átviteli tényezője ugyanezen a körfrekvencián $\bar{H} = 2 e^{- j 1, 2}$ . Határozza meg a rendszer válaszának időfüggvényét!*

Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza $h (t) = 20 δ (t) - 20 ε (t) e^{5 t}$ . Gerjesztés-válasz stabilis-e a rendszer?

Egy diszkrét idejű jel időfüggvénye a $x [k] = \cos [0, 75 π k + 4]$ . Állapítsa meg a jel $L$ periódushosszát!

Egy folytonos idejű, lineáris, invariáns rendszer impulzusválasza $h (t) = 20 δ (t) - 20 ε (t) e^{- 5 t}$ . Gerjesztés-válasz stabilis-e a rendszer?

Egy $L = 4$ periódusidejű jel komplex Fourier-együtthatói: $X_{0}^{C} = 1, X_{1}^{C} = 2 e^{j 0, 2}, X_{2}^{C} = 0$ . Adja meg a jel mérnöki valós alakjának megfelelő időfüggvényét!*

Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: $y (t) = 5 [u (t + 3)]$ . Jellemezze a rendszert!

Egy diszkrét idejű jel időfüggvénye a $x [k] = \cos [0, 4 π k + 4]$ . Állapítsa meg a jel $L$ periódushosszát!

Egy diszkrét idejű jel időfüggvénye $x [k] = 5 \cos [0, 5 π k - 0, 5]$ . Adja meg a jel fazorát (komplex csúcsértékét)!

Egy diszkrét idejű rendszer rendszeregyenlete $y [k] + 5 y [k - 1] = u [k] - 2 u [k - 1]$ . Adja meg a rendszer átviteli karakterisztikáját!

Explicit gerjesztés-válasz kapcsolattal adott az alábbi rendszer: $y (t) = 5 [u (t)]^{2}$ . Jellemezze a rendszert!

Egy folytonos idejű rendszer impulzusválasza $h (t) = 4 ε (t) e^{- 2 t}$ . Adja meg a rendszer ugrásválaszát!

Egy diszkrét idejű rendszer átviteli karakterisztikája $H (e^{j ϑ}) = \frac{e^{- j ϑ} + e^{- j 2 ϑ}}{1 + e^{- j ϑ} + e^{- j 2 ϑ}}$ . Adja meg a rendszer átviteli tényezőjét a $ϑ = \frac{π}{2}$ körfrekvencián!*