„Laboratórium 2 - 8. Mérés ellenőrző kérdései” változatai közötti eltérés
| (11 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 19. sor: | 19. sor: | ||
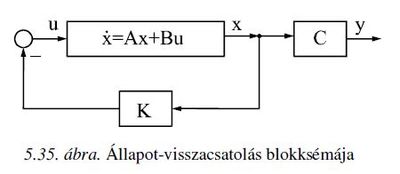
==3. Mit értünk állapot-visszacsatolás alatt? == | ==3. Mit értünk állapot-visszacsatolás alatt? == | ||
Azt, hogy u = -K*x , azaz a beavatkozó jel az állapotok lineáris kombinációjakért írható fel. | |||
[[File:Szabtech állapot-visszacsatolás ábra.JPG|400px]] | [[File:Szabtech állapot-visszacsatolás ábra.JPG|400px]] | ||
==4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete? == | ==4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete? == | ||
<math> det(A - BK - λI) = 0 </math> | |||
==5. Mik a fő problémák az egyszerű u=-Kx állapot-visszacsatolás esetén tipikus irányítási rendszerekben? == | ==5. Mik a fő problémák az egyszerű u=-Kx állapot-visszacsatolás esetén tipikus irányítási rendszerekben? == | ||
Az állapotok | Az állapotok gyakran nem mérhetőek közvetlenül, ezért becsülni kell őket. | ||
==6. Mi a domináns póluspár? == | ==6. Mi a domináns póluspár? == | ||
A zárt szabályozási kör átviteli függvényének '''nullához legközelebbi pólusát vagy konjugált komplex póluspárját''' a zárt rendszer domináns póluspárjának nevezzük. | A zárt szabályozási kör átviteli függvényének '''nullához legközelebbi pólusát vagy konjugált komplex póluspárját''' a zárt rendszer domináns póluspárjának nevezzük. | ||
Ökölszabályként elfogadható, hogy ha a többi pólus a domináns konjugált komplex póluspártól balra úgy helyezkedik el, hogy valós részének abszolút értéke legalább háromszor nagyobb a domináns póluspár valós részének abszolút értékénél, akkor a zárt rendszer átmeneti függvényének első maximuma helyén a többi pólus tranziense már lecseng, ezért '''a dinamikus minőségi jellemzőket a domináns póluspár határozza meg'''. | Ökölszabályként elfogadható, hogy ha a többi pólus a domináns konjugált komplex póluspártól balra úgy helyezkedik el, hogy valós részének abszolút értéke legalább háromszor nagyobb a domináns póluspár valós részének abszolút értékénél, akkor a zárt rendszer átmeneti függvényének (ugrásválaszának) első maximuma helyén a többi pólus tranziense már lecseng, ezért '''a dinamikus minőségi jellemzőket a domináns póluspár határozza meg'''. | ||
==7. Mi a kapcsolat a kéttárolós lengő tag csillapítása és csillapítatlan sajátfrekvenciája valamint a hozzátartozó pólusok között? == | ==7. Mi a kapcsolat a kéttárolós lengő tag csillapítása és csillapítatlan sajátfrekvenciája valamint a hozzátartozó pólusok között? == | ||
| 49. sor: | 49. sor: | ||
==10. Mi a kapcsolat a "terhelés" elnevezés és a zavaró jel között? == | ==10. Mi a kapcsolat a "terhelés" elnevezés és a zavaró jel között? == | ||
A | A konstans terhelés megfeleltethető a bemenetre redukált konstans zavarással. | ||
==11. Hogyan küszöbölhető ki a terhelés hatása? == | ==11. Hogyan küszöbölhető ki a terhelés hatása? == | ||
| 57. sor: | 57. sor: | ||
Diszkrétidejű rendszereknél célszerű kihasználni, hogy a t = iT pillanatban már rendelkezésre áll y[i], ezért ha ezt a szabályozóban már figyelembe vesszük, akkor egy T ütemnyi holtidőt eliminálni tudunk a szabályozóban. | Diszkrétidejű rendszereknél célszerű kihasználni, hogy a t = iT pillanatban már rendelkezésre áll y[i], ezért ha ezt a szabályozóban már figyelembe vesszük, akkor egy T ütemnyi holtidőt eliminálni tudunk a szabályozóban. | ||
Másik megfogalmazás: | |||
Az aktuális állapotmegfigyelő egy diszkrét idejű időinvarináns lineáris dinamikus rendszer, amelynek kimenete az 𝑥̂<sub>i</sub> becsült állapot: | |||
<math>x̂_{i} = Fx̂_{i-1} + Gy_{i} + Hu_{i-1} </math> | |||
Előnyei: | |||
* F, G és H megfelelő megválasztásával a becslési hiba 0-ra csökkenthető | |||
* mivel a kimenet aktuális értékét használja, így kiküszöböl egy mintavételi időnyi holtidőt | |||
==13. Miért érdemes integrátort tenni a szabályozási körbe? == | ==13. Miért érdemes integrátort tenni a szabályozási körbe? == | ||
A (konstans) zavaró hatás kiküszöbölhető vele. | |||
==14. Hogyan képződik le egy folytonos idejű pólus a diszkrétidejű tartományba? == | ==14. Hogyan képződik le egy folytonos idejű pólus a diszkrétidejű tartományba? == | ||
<math>z = e^{sT} </math> , ahol T a mintavételi periódusidő | |||
==15. Mit okoznak a megfigyelő sajátértékei a zárt rendszer átviteli függvényében? == | ==15. Mit okoznak a megfigyelő sajátértékei a zárt rendszer átviteli függvényében? == | ||
A lap jelenlegi, 2023. március 30., 10:06-kori változata
Oktatói kérésre a válaszok kitörölve (túl nagy átfedést mutattak az oktatói segédlettel). Ha jól értelmeztem, saját szavakkal megfogalmazva beírhatjátok a válaszokat - Kozaróczy Zsolt (vita) 2015. március 24., 12:37 (UTC)
1. Milyen identifikációs rendszermodelleket ismer?
- AR (autoregresszív)
- MA (moving average - mozgóátlag)
- X (exegenous signal - külső bemenőjelet tartalmazó)
- OE (output error - kimenetre redukált additív zajt tartalmazó)
- BJ (Box-Jenkins modell)
- PEM (parameter estimation model - általános lineáris paraméterbecslési modell)
2. Miért van szükség identifikációra?
Identifikáció segítségével tudunk egy szakaszról modellt alkotni (meghatározni a sajátértékeit, pólusait, zérusait, időállandóit, stb.). Ehhez a modellhez tervezzük a szabályozót.
3. Mit értünk állapot-visszacsatolás alatt?
Azt, hogy u = -K*x , azaz a beavatkozó jel az állapotok lineáris kombinációjakért írható fel.
4. Mi lesz állapot-visszacsatolás esetén a zárt rendszer karakterisztikus egyenlete?
Értelmezés sikertelen (formai hiba): {\displaystyle det(A - BK - λI) = 0 }
5. Mik a fő problémák az egyszerű u=-Kx állapot-visszacsatolás esetén tipikus irányítási rendszerekben?
Az állapotok gyakran nem mérhetőek közvetlenül, ezért becsülni kell őket.
6. Mi a domináns póluspár?
A zárt szabályozási kör átviteli függvényének nullához legközelebbi pólusát vagy konjugált komplex póluspárját a zárt rendszer domináns póluspárjának nevezzük. Ökölszabályként elfogadható, hogy ha a többi pólus a domináns konjugált komplex póluspártól balra úgy helyezkedik el, hogy valós részének abszolút értéke legalább háromszor nagyobb a domináns póluspár valós részének abszolút értékénél, akkor a zárt rendszer átmeneti függvényének (ugrásválaszának) első maximuma helyén a többi pólus tranziense már lecseng, ezért a dinamikus minőségi jellemzőket a domináns póluspár határozza meg.
7. Mi a kapcsolat a kéttárolós lengő tag csillapítása és csillapítatlan sajátfrekvenciája valamint a hozzátartozó pólusok között?
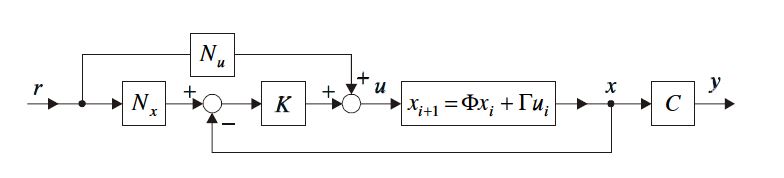
8. Mi biztosítja a konstans alapjel követését állapot-visszacsatolt rendszerekben?
Az alapjelet az Nx és Nu segítségével vesszük figyelembe. Ezeket a végértékek alapján határozhatjuk meg. Pl. egységugrás alapjel esetén: r[∞]=1, e[∞]=0, y[∞]=1, valamint x[k+1]=x[k] felhasználásával. Beépítésük a szabályozóba az ábrán látható.
9. Miért szükséges állapotmegfigyelő alkalmazása?
Az állapot-visszacsatolásban szereplő x állapot általában nem mérhető (az érzékelő szervek csak az y kimenetet mérik), ezért helyettesíteni kell valamilyen x̂ becsléssel. Ha a jelek determinisztikusak, akkor az x̂ -ot meghatározó egységet állapotmegfigyelőnek nevezzük, mely a szakasz ismert u bemenete és mért y kimenete alapján számít becslést x -re.
10. Mi a kapcsolat a "terhelés" elnevezés és a zavaró jel között?
A konstans terhelés megfeleltethető a bemenetre redukált konstans zavarással.
11. Hogyan küszöbölhető ki a terhelés hatása?
Terhelésbecslő alkalmazásával. Ekkor a terhelést konstansnak feltételezzük, de értékét nem ismerjük előre, állapotváltozónak tekintjük, és úgy vesszük, hogy a szakasz elején adódik hozzá a beavatkozó jelhez (u).
12. Mit értünk diszkrétidejű aktuális megfigyelő alatt és mik az előnyei?
Diszkrétidejű rendszereknél célszerű kihasználni, hogy a t = iT pillanatban már rendelkezésre áll y[i], ezért ha ezt a szabályozóban már figyelembe vesszük, akkor egy T ütemnyi holtidőt eliminálni tudunk a szabályozóban.
Másik megfogalmazás: Az aktuális állapotmegfigyelő egy diszkrét idejű időinvarináns lineáris dinamikus rendszer, amelynek kimenete az 𝑥̂i becsült állapot:
Értelmezés sikertelen (formai hiba): {\displaystyle x̂_{i} = Fx̂_{i-1} + Gy_{i} + Hu_{i-1} }
Előnyei:
- F, G és H megfelelő megválasztásával a becslési hiba 0-ra csökkenthető
- mivel a kimenet aktuális értékét használja, így kiküszöböl egy mintavételi időnyi holtidőt
13. Miért érdemes integrátort tenni a szabályozási körbe?
A (konstans) zavaró hatás kiküszöbölhető vele.
14. Hogyan képződik le egy folytonos idejű pólus a diszkrétidejű tartományba?
, ahol T a mintavételi periódusidő