„Számítógépes látórendszerek - Ellenőrző kérdések: Javítás képtartományban” változatai közötti eltérés
/* Ismertesse az élkeresés alapvető módszereit: DoG, első és második deriváltak, Canny, Frei & Chen (a konkrét kernelek nem szükségesek). Hogyan lehet az élkeresés eredményén javítani ha több-féle eljárásra is lehetőségünk n… |
a autoedit v2: fájlhivatkozások egységesítése, az új közvetlenül az adott fájlra mutat |
||
| (28 közbenső módosítás, amit 3 másik szerkesztő végzett, nincs mutatva) | |||
| 10. sor: | 10. sor: | ||
A digitális fényképészet gyakran használ hisztogramot. A jól felszerelt digitális fényképezőgépek valós időben mutatnak hisztogramokat, hogy így segítsék a képi egyensúly megtalálását. Ez pontosabb képszerkesztést tesz lehetővé, mint ami a kamerakép alapján tehetséges lehetne. Felismerhetők és javíthatók például a világítás hibái, ha a kép túl sötét vagy túl világos lenne. A kép későbbi feldolgozásában sokat számítanak a rajta levő kontrasztok és a fényességek, ezért érdemes a hisztogramokat figyelni. | A digitális fényképészet gyakran használ hisztogramot. A jól felszerelt digitális fényképezőgépek valós időben mutatnak hisztogramokat, hogy így segítsék a képi egyensúly megtalálását. Ez pontosabb képszerkesztést tesz lehetővé, mint ami a kamerakép alapján tehetséges lehetne. Felismerhetők és javíthatók például a világítás hibái, ha a kép túl sötét vagy túl világos lenne. A kép későbbi feldolgozásában sokat számítanak a rajta levő kontrasztok és a fényességek, ezért érdemes a hisztogramokat figyelni. | ||
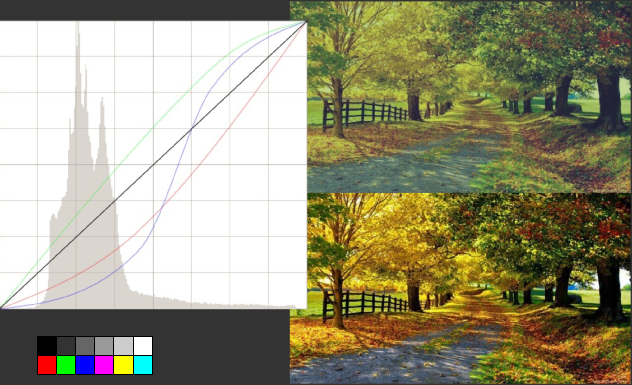
A hisztogramok egy klasszikus felhasználása a színegyensúly beállítása (equalizing). A hisztogramot és a megfelelő színeket egy alkalmas függvénnyel transzformálják. Jobban kiegyensúlyozza a színeket, mint a kontrasztok erősítése. | A hisztogramok egy klasszikus felhasználása a színegyensúly beállítása ('''equalizing'''), lásd az ábrát. A hisztogramot és a megfelelő színeket egy alkalmas függvénnyel transzformálják. Jobban kiegyensúlyozza a színeket, mint a kontrasztok erősítése. Az ábrán bal alsó sarokban látható néhány szín a korrekció paramétereinek beállításához használható referencia, az erről készült fényképet úgy kell korrigálni, hogy a képen az eredeti értékeket kapjuk vissza (persze ilyen komolyságnál már arra is vigyázni kell hogy a minta megfakul idővel stb.). | ||
[http://hu.wikipedia.org/wiki/Hisztogram Forrás] | [http://hu.wikipedia.org/wiki/Hisztogram Forrás] | ||
[[File:Számítógépes látórendszerek Színkorrekció.png]] | |||
== Milyen fontosabb zajok jellemezhetik a képeket? <br/>Sorolja fel a lehetséges eljárásokat ezek eltüntetésére? <br/>Ismertesse a konvolúciós ablakkal történő képjavítás módszerét. == | == Milyen fontosabb zajok jellemezhetik a képeket? <br/>Sorolja fel a lehetséges eljárásokat ezek eltüntetésére? <br/>Ismertesse a konvolúciós ablakkal történő képjavítás módszerét. == | ||
| 29. sor: | 32. sor: | ||
*Élesítő szűrők | *Élesítő szűrők | ||
*Rank szűrők | *Rank szűrők | ||
*Median | **Median | ||
===Konvolúciós ablak=== | ===Konvolúciós ablak=== | ||
| 55. sor: | 58. sor: | ||
===[ 1 2 1 ; 2 4 2 ; 1 2 1 ] kernel előnyei=== | ===[ 1 2 1 ; 2 4 2 ; 1 2 1 ] kernel előnyei=== | ||
FPGA-ban nagyon könnyű megvalósítani | FPGA-ban nagyon könnyű megvalósítani, mivel 2-vel és 4-gyel kell szorozni, 16-tal kell osztani a végén. Ezek a műveletek a 2-hatványok miatt eltolások, FPGA-ban csupán huzalozással megoldhatók. | ||
===Gauss szűrő=== | ===Gauss szűrő=== | ||
| 80. sor: | 83. sor: | ||
===Rank-szűrők=== | ===Rank-szűrők=== | ||
A | A simító szűrők a zajhatásokat csak szétosztják (szétkenik, kiátlagolják), ezzel szemben a Rank-szűrők szinte teljesen képesek megszabadítani a képet ezektől a pontszerű hibáktól. | ||
Működési elv: Vesszük minden pixel meghatározott környezetét. A pixel és a környezet intenzitásértékeit nagyság szerinti növekvő sorrendbe állítjuk. E sorból vegyük az n-edik elemet; ez lesz a pixel új világosságértéke. | |||
Működési elv: Vesszük minden pixel meghatározott környezetét. A pixel és a környezet intenzitásértékeit nagyság szerinti növekvő sorrendbe állítjuk. E sorból vegyük az n-edik elemet; ez lesz a pixel új világosságértéke. | |||
Ha n=1, akkor mindig a minimális értéket választottuk, ha n=k, akkor mindig a k-adikat. Median szűrésről akkor beszélünk, ha n=k/2, vagyis a sorba rendezett világosságértékek közül éppen a középsőt választjuk. A vizsgált pixelkörnyezet mérete, alakja sokféleképpen választható. | |||
*k-adik szomszéd | *k-adik szomszéd | ||
| 94. sor: | 100. sor: | ||
===Kernelméret, kernel többszörös végrehajtása=== | ===Kernelméret, kernel többszörös végrehajtása=== | ||
Általában 3x3,5x5 -ös kernelméreteket használnak | Általában 3x3, 5x5-ös kernelméreteket használnak. Van 7x7-es is, de ez valós időben nem mindig használható. | ||
A | A medián szűrőt például sokszor egymás után végrehajtják, így teljesen eltűnnek a zajcsúcsok. | ||
=== Egyéb === | |||
==== Olimpiai szűrő ==== | |||
Az olimpiai szűrő, a medián szűrőhöz hasonlóan, a kiugró intenzitás értékeket zajforrásból származónak tekinti. Egyes sportok olimpiai pontozási módszerét követi. Sorba rendezi a kernel alatti elemeket, majd a középsőtől legjobban elütőket eldobja. Paraméterként megadható, hogy a legnagyobb és legkisebb elemekből mennyit hagy figyelmen kívül. | |||
[http://tarsadalominformatika.elte.hu/tananyagok/opensourceelm/lecke15_lap1.html#hiv3 Forrás] | |||
==== Kalap-szűrő ==== | |||
Ha kisebb a "szennyeződés" mint a belső kör fele, akkor azt eltünteti a szűrő. | |||
== Ismertesse az élkeresés alapvető módszereit: <br/>DoG, első és második deriváltak, Canny, Frei & Chen (a konkrét kernelek nem szükségesek). <br/>Hogyan lehet az élkeresés eredményén javítani ha több-féle eljárásra is lehetőségünk nyílik (pl. Sobel)? <br/>Hogyan hat a kernelméret az élkeresésre? == | == Ismertesse az élkeresés alapvető módszereit: <br/>DoG, első és második deriváltak, Canny, Frei & Chen (a konkrét kernelek nem szükségesek). <br/>Hogyan lehet az élkeresés eredményén javítani ha több-féle eljárásra is lehetőségünk nyílik (pl. Sobel)? <br/>Hogyan hat a kernelméret az élkeresésre? == | ||
| 101. sor: | 114. sor: | ||
===Élkeresés alapvető módszerei=== | ===Élkeresés alapvető módszerei=== | ||
==== DoG(Gaussok különbsége) ==== | |||
Az eredeti képen két különböző Gauss szűrést végzünk.(Az egyik nagyobb mértékben simít mint a másik.)<br/> A végső képet úgy kapjuk meg, hogy az eredeti képben minden pixelt a két Gauss szűrt kép különbségével(pixelenként természetesen)helyettesítünk. <br/>A nullátmenetek (ahol a pozitív értékekből negatív lesz és fordítva) fontosak a számunkra, ezek gyakorlatilag az élek. | Az eredeti képen két különböző Gauss szűrést végzünk.(Az egyik nagyobb mértékben simít mint a másik.)<br/> A végső képet úgy kapjuk meg, hogy az eredeti képben minden pixelt a két Gauss szűrt kép különbségével(pixelenként természetesen)helyettesítünk. <br/>A nullátmenetek (ahol a pozitív értékekből negatív lesz és fordítva) fontosak a számunkra, ezek gyakorlatilag az élek. | ||
# | ==== Deriváltak ==== | ||
# | '''Első derivált''': | ||
#Frei & Chen | *[ X X X ; -1 0 1 ; X X X ] | ||
*[ -1 X X ; X 0 X ; X X 1 ] | |||
'''Második derivált''': | |||
*[ X X X ; -1 2 -1 ; X X X ] | |||
*[ -1 X X ; X 2 X ; X X -1 ]<br/> | |||
X: don't care | |||
==== Canny ==== | |||
Elsősorban lépcsős élekre, a kép Gauss zajjal terhelt. | |||
Lépések | |||
# Gauss szűrés | |||
# Derivatív szűrés két/négy irányban | |||
# Nem maximumok törlése (gradiens irányban) | |||
# Küszöbözés: erős élek, gyenge élek | |||
==== Frei & Chen ==== | |||
Kevésbé érzékeny a zajokra mint más élkereső eljárások. Összesen 9 konvolúciós ablakot/kernelt használ(3x3 méret), ezek a legfontosabb irányú kernelek. | |||
===Többféle élkeresési eljárás=== | |||
==== Sobel ==== | |||
===Kernelméret és az élkeresés=== | |||
Minél nagyobb a kernelméret annál inkább eltűnnek az apró dolgok. | |||
== Milyen jellegű geometriai torzítások terhelhetik a képet? <br/>Ismertesse a perspektív illetve a radiális és tangenciális torzítás hatását és kezelésének módját. <br/>Hogyan tudjuk visszaállítani az eredeti arányokat egy ferde kamerával követett síkbeli képen? == | == Milyen jellegű geometriai torzítások terhelhetik a képet? <br/>Ismertesse a perspektív illetve a radiális és tangenciális torzítás hatását és kezelésének módját. <br/>Hogyan tudjuk visszaállítani az eredeti arányokat egy ferde kamerával követett síkbeli képen? == | ||
=== Perspektív === | |||
Gyakorlatban: Ha egy épületet az utcán állva fotózunk, gyakran azt tapasztaljuk, hogy a képen a függőleges vonalak összefutnak. Ez a perspektivikus torzítás, ami általában hibának számít. Még erőteljesebb a hatás, ha nagy látószögű objektívvel, viszonylag közelről fényképezünk. Bár az utómunka során ezt a hibát elvben korrigálni lehet, de az újabb torzulásokkal járhat. Ezért a legjobb a felvételkor elvégezni a korrekciót. | |||
[http://www.fotovilag.hu/cikk/291/ Forrás] | |||
=== Radiális === | |||
Ezt a fajta torzítást az okozza, hogy az eszközökben az olcsóbb kivitelezhetőség miatt ideális parabolikus lencsék helyett gömbszerű lencséket | |||
alkalmaznak, valamint a képalkotó általában nem a lencse fókuszpontjában helyezkedik el. Ez a torzítás okozza az ún. hordó, vagy halszem effektust. A lencse közepétől távolabb eső fénysugarak jobban elhajlanak, mint a lencse közepén. Ez olcsó webkamerák esetén jól megfigyelhető, drága, csúcskategóriás eszközöknél igyekeznek a matematikailag ideálist jobban megközelítő lencsét előállítani, illetve a képalkotót a fókuszpontba helyezni. A radiális torzítás a kép közepén 0, és a kép szélei felé haladva növekszik. | |||
[https://www.google.hu/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&ved=0CCoQFjAC&url=http%3A%2F%2Fwww.tankonyvtar.hu%2Fen%2Ftartalom%2Ftamop422b%2F2010-0020_0053_nik_pub_kemenes_palyamunka_20029_0184%2F0053_nik_pub_kemenes_palyamunka_20029_0184.pdf&ei=ZKt2Va-UN8XtUqrtgOAD&usg=AFQjCNHd_3KXFdRfK_xJZ236Hv4acFPVzQ&sig2=X4LTc80WY6a_gGosVqaLUA&cad=rja Forrás] | |||
=== Tangenciális === | |||
Ez a fajta torzítás a gyártás hibáiból adódik, a lencse nem párhuzamos a képalkotóval. Ez a torzítás két paraméterrel ( <math>p_{1}, p_{2})</math> adható meg. | |||
[https://www.google.hu/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&ved=0CCoQFjAC&url=http%3A%2F%2Fwww.tankonyvtar.hu%2Fen%2Ftartalom%2Ftamop422b%2F2010-0020_0053_nik_pub_kemenes_palyamunka_20029_0184%2F0053_nik_pub_kemenes_palyamunka_20029_0184.pdf&ei=ZKt2Va-UN8XtUqrtgOAD&usg=AFQjCNHd_3KXFdRfK_xJZ236Hv4acFPVzQ&sig2=X4LTc80WY6a_gGosVqaLUA&cad=rja Forrás] | |||
== Milyen interpolációs technikákat ismer? <br/>Ismertesse a legközelebbi szomszéd, a bilineáris és a biköbös interpolációs technikák alapelvét (képletek nem szükségesek). == | == Milyen interpolációs technikákat ismer? <br/>Ismertesse a legközelebbi szomszéd, a bilineáris és a biköbös interpolációs technikák alapelvét (képletek nem szükségesek). == | ||
Ebben az értelemben az adott mennyiségű képpontból nagyobb (vagy kisebb) felbontású, több (vagy kevesebb) képpontot tartalmazó képet állítunk elő. Motiválhatja például a [http://en.wikipedia.org/wiki/Image_scaling kép nagyítás]ának igénye. Nagyításnál egyértelműen hiányzó információt pótolunk, kicsinyítéskor viszont a pixelek elhelyezkedésének változása miatt szükséges interpolálni (azonos | Ebben az értelemben az adott mennyiségű képpontból nagyobb (vagy kisebb) felbontású, több (vagy kevesebb) képpontot tartalmazó képet állítunk elő. Motiválhatja például a [http://en.wikipedia.org/wiki/Image_scaling kép nagyítás]ának igénye. Nagyításnál egyértelműen hiányzó információt pótolunk, kicsinyítéskor viszont a pixelek elhelyezkedésének változása miatt szükséges interpolálni (azonos képtartalmat kevesebb, jellemzően más pozícióba kerülő adatponttal ábrázolunk). | ||
* '''[http://en.wikipedia.org/wiki/Nearest-neighbor_interpolation Legközelebbi szomszéd]''': A nagyított kép egyes pixeleinek értékeit az alapján határozzuk meg, hogy melyik eredeti pixelhez vannak legközelebb, azzal tesszük őket egyenlővé. ''Pixeles'' képet eredményez. | * '''[http://en.wikipedia.org/wiki/Nearest-neighbor_interpolation Legközelebbi szomszéd]''': A nagyított kép egyes pixeleinek értékeit az alapján határozzuk meg, hogy melyik eredeti pixelhez vannak legközelebb, azzal tesszük őket egyenlővé. ''Pixeles'' képet eredményez. | ||
* '''[http://en.wikipedia.org/wiki/Bilinear_interpolation Bilineáris]''': Az új pixelek értékét mindkét irányban lineárisan interpoláljuk (név innen), azaz egyenest illesztünk a két közeli eredeti pixel érték közé, és a keresett érték az egyenes pixelnek megfelelő helyén felvett értéke lesz. Az egyenesillesztést tehát a legközelebbi 4 pixel alapján hajtjuk végre. Furcsa ''artifact''-okat tud okozni, viszont nagyon gyors. | * '''[http://en.wikipedia.org/wiki/Bilinear_interpolation Bilineáris]''': Az új pixelek értékét mindkét irányban lineárisan interpoláljuk (név innen), azaz egyenest illesztünk a két közeli eredeti pixel érték közé, és a keresett érték az egyenes pixelnek megfelelő helyén felvett értéke lesz. Az egyenesillesztést tehát a legközelebbi 4 pixel alapján hajtjuk végre. Furcsa ''artifact''-okat tud okozni, viszont nagyon gyors. | ||
* '''[http://en.wikipedia.org/wiki/Bicubic_interpolation Biköbös (bicubic)]''': Lassabb a bilineárisnál, de szebb eredményt is ad. A legközelebbi 16 pixel alapján számol. Figyelembe veszi a szomszédos pixel értékeket, az x-y irányú deriváltakat és kereszt deriváltakat, az ezekből következő meredekségi kényszerekre felírt egyenleteket oldja meg. | * '''[http://en.wikipedia.org/wiki/Bicubic_interpolation Biköbös (bicubic)]''': Lassabb a bilineárisnál, de szebb eredményt is ad. A legközelebbi 16 pixel alapján számol. Figyelembe veszi a szomszédos pixel értékeket, az x-y irányú deriváltakat és kereszt deriváltakat, az ezekből következő meredekségi kényszerekre felírt egyenleteket oldja meg. | ||
* [http://en.wikipedia.org/wiki/Lanczos_resampling Lánczos] | * [http://en.wikipedia.org/wiki/Lanczos_resampling Lánczos] | ||
* Komplex megoldások | * Komplex megoldások | ||
| 125. sor: | 174. sor: | ||
Képi matematika esetén végezhetünk műveleteket '''kép-érték''' vagy '''kép-kép''' között. | Képi matematika esetén végezhetünk műveleteket '''kép-érték''' vagy '''kép-kép''' között. | ||
=== Lehetséges műveletek === | |||
* összeadás/kivonás/átlagolás | * összeadás/kivonás/átlagolás | ||
* szorzás/osztás/normalizálás | * szorzás/osztás/normalizálás | ||
| 131. sor: | 180. sor: | ||
* logikai műveletek (főleg bináris képeknél) | * logikai műveletek (főleg bináris képeknél) | ||
Gyakorlati alkalmazás | === Gyakorlati alkalmazás === | ||
* Kép-érték esetben az összeadás fényerő állítást jelent, a szorzás brightness/contrast állítást.[?] | * Kép-érték esetben az összeadás fényerő állítást jelent, a szorzás brightness/contrast állítást.[?] | ||
* A szorzás művelet használható textúrázásra (maszkolásra). | * A szorzás művelet használható textúrázásra (maszkolásra). | ||
* Az összeadás/átlagolás használható zajcsökkentésre. | * Az összeadás/átlagolás használható zajcsökkentésre. | ||
* A kivonás használható különbségképzésre, a háttér eltávolítására (mozgó/elmozdult objektumok keresésére). | * A kivonás használható különbségképzésre, a háttér eltávolítására (mozgó/elmozdult objektumok keresésére). | ||
A lap jelenlegi, 2017. július 12., 15:09-kori változata
Mit jelent a hisztogram?
Ismertesse a hisztogramtranszformáció működését és felhasználási lehetőségeit.
Hisztogram
A kép hisztogramja a fényességértékek vagy az egyes színcsatornákon felvett értékeinek eloszlását (sűrűségfüggvényét) mutatja. A lehetséges színértékek tengelyére az egyes színértékek gyakoriságát viszik fel. Minél magasabb ez, annál többször fordul elő az adott színérték a képen.
A digitális képfeldolgozásban a hisztogram a kép színértékeiről vagy szürkeségi fokozatáról készül. Ez alapján adatok nyerhetők az előforduló színekről, kontrasztokról és fényességekről. Egy színes képről több hisztogram is készíthető az egyes színcsatornák, vagy az összes szín szerint. Mivel a legtöbb eljárás a fekete-fehér képeket támogatja, ezért inkább az egyes színcsatornák hisztogramját használják, ami lehetővé teszi a kép feldolgozásának azonnali folytatását. A színcsatornák száma az alapszínek számától függ: RGB estén három, CMYK esetén négy.
Működés, felhasználás
A digitális fényképészet gyakran használ hisztogramot. A jól felszerelt digitális fényképezőgépek valós időben mutatnak hisztogramokat, hogy így segítsék a képi egyensúly megtalálását. Ez pontosabb képszerkesztést tesz lehetővé, mint ami a kamerakép alapján tehetséges lehetne. Felismerhetők és javíthatók például a világítás hibái, ha a kép túl sötét vagy túl világos lenne. A kép későbbi feldolgozásában sokat számítanak a rajta levő kontrasztok és a fényességek, ezért érdemes a hisztogramokat figyelni.
A hisztogramok egy klasszikus felhasználása a színegyensúly beállítása (equalizing), lásd az ábrát. A hisztogramot és a megfelelő színeket egy alkalmas függvénnyel transzformálják. Jobban kiegyensúlyozza a színeket, mint a kontrasztok erősítése. Az ábrán bal alsó sarokban látható néhány szín a korrekció paramétereinek beállításához használható referencia, az erről készült fényképet úgy kell korrigálni, hogy a képen az eredeti értékeket kapjuk vissza (persze ilyen komolyságnál már arra is vigyázni kell hogy a minta megfakul idővel stb.).
Milyen fontosabb zajok jellemezhetik a képeket?
Sorolja fel a lehetséges eljárásokat ezek eltüntetésére?
Ismertesse a konvolúciós ablakkal történő képjavítás módszerét.
Zajok
Gauss zaj: Az erősítő képzaja. Gyenge megvilágítás, magas hőmérséklet és a fényképező elektronikája által okozott zaj.
Só-bors zaj: A kép fekete és fehér pixelekkel van "megszórva". A/D konverziós, átviteli hibák okozzák.
Digitális zaj típusok jellemzése
Eljárások a zajok eltüntetésére
- Egyszerű átlagolás
- Konvolúció
- Gauss szűrés
- Simító szűrők
- Élesítő szűrők
- Rank szűrők
- Median
Konvolúciós ablak
A kép adott pixelét a környezetében lévő pixelek függvényében módosítjuk. Pixelről pixelre haladunk.
Az ablak (kernel, maszk) egy mátrix, elemei a súlyok. Lineáris esetben minden pixelt a környezetének lineáris kombinációjával helyettesítjük.
A lineáris kombinációval történő leírást konvolúciós kernelnek nevezzük.
A képjavítás menete:
- Az input minden pixelére egy ablakot/kernelt helyezünk úgy, hogy annak origója az adott pixelre essen.
- Az input kép kernelében lévő pixeleit megszorozzuk a kernelben szereplő súlyokkal.
- Az eredmény: az input helyzetének megfelelő pixel értéke a súlyozott értékek összege(esetleg skálázva).
Hogyan tudunk simító szűrőt készíteni?
Hogyan hat a képre a konvolúciós kernel mérete és a kernelen belüli értékek elrendezése?
Milyen előnyei vannak az alábbi kernelnek: [ 1 2 1 ; 2 4 2 ; 1 2 1 ]?
Ismertesse a Gauss szűrő lényegét.
Simító szűrő
Simítás lényege, hogy a képpontok közelebb kerülnek környezetük átlagához, azaz a kép „simább” lesz, Vesszük a sima átlagoló szűrő kernelét, de különböző súlyozásokat használunk. A kernel elemei pozitívak.
Konvolúciós kernel mérete
Minél nagyobb a kernel, az apróbb dolgok annál inkább eltűnnek, elmosódnak.
[ 1 2 1 ; 2 4 2 ; 1 2 1 ] kernel előnyei
FPGA-ban nagyon könnyű megvalósítani, mivel 2-vel és 4-gyel kell szorozni, 16-tal kell osztani a végén. Ezek a műveletek a 2-hatványok miatt eltolások, FPGA-ban csupán huzalozással megoldhatók.
Gauss szűrő
Kernelméret 3σ. Kernel: [1 4 1; 4 16 4 ; 1 4 1]. Egyenlő súly helyett érdemesebb a közelebbi pixeleket nagyobb súllyal számolni.
A Gauss szűrő simító jellegű.Szépen elkeni a képet, viszont nem túl gyors. Algoritmusokban van szerepe, pl. a Canny-féle éldetektorban használjuk.
Hogyan működnek az élesítő szűrők?
Miben különbözik egy élesítő és egy élkereső szűrő?
Milyen változtatást hajt végre a képen az alábbi szűrő: [ -2 -1 0 ; -1 1 1 ; 0 1 2 ]?
Élesítő szűrők
Kiemeli a környezeti átlagtól való eltérést (azaz az éleket). A kernelben vannak pozitív és negatív súlyok is. Minél nagyobb a középső érték annál inkább hasonlít az eredeti képre az új. Hátrány: a zajokat is kiemeli.
Élesítő vs élkereső szűrő
Élkereső szűrő esetén a kernel súlyainak összege nulla, míg élesítőnél nem. A nullával nem osztunk, hanem eltoljuk egy félszürkeárnyalattal.
[ -2 -1 0 ; -1 1 1 ; 0 1 2 ] szűrő
Ez térbeli kiemelésre használatos. Gyakorlatilag azonban ez is élkiemelés. Csak önmagában, mint élesítés nem használják.
Milyen rank-szűrőket ismerünk, ismertesse ezek használatát.
Milyen előnyei vannak a median szűrőnek.
Hogyan hat a szűrésre a kernelméret és a kernel többszörös végrehajtása?
Rank-szűrők
A simító szűrők a zajhatásokat csak szétosztják (szétkenik, kiátlagolják), ezzel szemben a Rank-szűrők szinte teljesen képesek megszabadítani a képet ezektől a pontszerű hibáktól.
Működési elv: Vesszük minden pixel meghatározott környezetét. A pixel és a környezet intenzitásértékeit nagyság szerinti növekvő sorrendbe állítjuk. E sorból vegyük az n-edik elemet; ez lesz a pixel új világosságértéke.
Ha n=1, akkor mindig a minimális értéket választottuk, ha n=k, akkor mindig a k-adikat. Median szűrésről akkor beszélünk, ha n=k/2, vagyis a sorba rendezett világosságértékek közül éppen a középsőt választjuk. A vizsgált pixelkörnyezet mérete, alakja sokféleképpen választható.
- k-adik szomszéd
- Minimum szűrő
- Maximum szűrő
- Median szűrő
Median szűrő előnyei
Előnye, hogy a finom dolgok finomak maradnak, viszont a tüskék eltűnnek. Vagy másképpen: ez a szűrés a kiugró zajcsúcsokat teljesen eltünteti és nem csak elkeni, mint a lineáris szűrés.
Kernelméret, kernel többszörös végrehajtása
Általában 3x3, 5x5-ös kernelméreteket használnak. Van 7x7-es is, de ez valós időben nem mindig használható. A medián szűrőt például sokszor egymás után végrehajtják, így teljesen eltűnnek a zajcsúcsok.
Egyéb
Olimpiai szűrő
Az olimpiai szűrő, a medián szűrőhöz hasonlóan, a kiugró intenzitás értékeket zajforrásból származónak tekinti. Egyes sportok olimpiai pontozási módszerét követi. Sorba rendezi a kernel alatti elemeket, majd a középsőtől legjobban elütőket eldobja. Paraméterként megadható, hogy a legnagyobb és legkisebb elemekből mennyit hagy figyelmen kívül. Forrás
Kalap-szűrő
Ha kisebb a "szennyeződés" mint a belső kör fele, akkor azt eltünteti a szűrő.
Ismertesse az élkeresés alapvető módszereit:
DoG, első és második deriváltak, Canny, Frei & Chen (a konkrét kernelek nem szükségesek).
Hogyan lehet az élkeresés eredményén javítani ha több-féle eljárásra is lehetőségünk nyílik (pl. Sobel)?
Hogyan hat a kernelméret az élkeresésre?
Élkeresés alapvető módszerei
DoG(Gaussok különbsége)
Az eredeti képen két különböző Gauss szűrést végzünk.(Az egyik nagyobb mértékben simít mint a másik.)
A végső képet úgy kapjuk meg, hogy az eredeti képben minden pixelt a két Gauss szűrt kép különbségével(pixelenként természetesen)helyettesítünk.
A nullátmenetek (ahol a pozitív értékekből negatív lesz és fordítva) fontosak a számunkra, ezek gyakorlatilag az élek.
Deriváltak
Első derivált:
- [ X X X ; -1 0 1 ; X X X ]
- [ -1 X X ; X 0 X ; X X 1 ]
Második derivált:
- [ X X X ; -1 2 -1 ; X X X ]
- [ -1 X X ; X 2 X ; X X -1 ]
X: don't care
Canny
Elsősorban lépcsős élekre, a kép Gauss zajjal terhelt. Lépések
- Gauss szűrés
- Derivatív szűrés két/négy irányban
- Nem maximumok törlése (gradiens irányban)
- Küszöbözés: erős élek, gyenge élek
Frei & Chen
Kevésbé érzékeny a zajokra mint más élkereső eljárások. Összesen 9 konvolúciós ablakot/kernelt használ(3x3 méret), ezek a legfontosabb irányú kernelek.
Többféle élkeresési eljárás
Sobel
Kernelméret és az élkeresés
Minél nagyobb a kernelméret annál inkább eltűnnek az apró dolgok.
Milyen jellegű geometriai torzítások terhelhetik a képet?
Ismertesse a perspektív illetve a radiális és tangenciális torzítás hatását és kezelésének módját.
Hogyan tudjuk visszaállítani az eredeti arányokat egy ferde kamerával követett síkbeli képen?
Perspektív
Gyakorlatban: Ha egy épületet az utcán állva fotózunk, gyakran azt tapasztaljuk, hogy a képen a függőleges vonalak összefutnak. Ez a perspektivikus torzítás, ami általában hibának számít. Még erőteljesebb a hatás, ha nagy látószögű objektívvel, viszonylag közelről fényképezünk. Bár az utómunka során ezt a hibát elvben korrigálni lehet, de az újabb torzulásokkal járhat. Ezért a legjobb a felvételkor elvégezni a korrekciót. Forrás
Radiális
Ezt a fajta torzítást az okozza, hogy az eszközökben az olcsóbb kivitelezhetőség miatt ideális parabolikus lencsék helyett gömbszerű lencséket alkalmaznak, valamint a képalkotó általában nem a lencse fókuszpontjában helyezkedik el. Ez a torzítás okozza az ún. hordó, vagy halszem effektust. A lencse közepétől távolabb eső fénysugarak jobban elhajlanak, mint a lencse közepén. Ez olcsó webkamerák esetén jól megfigyelhető, drága, csúcskategóriás eszközöknél igyekeznek a matematikailag ideálist jobban megközelítő lencsét előállítani, illetve a képalkotót a fókuszpontba helyezni. A radiális torzítás a kép közepén 0, és a kép szélei felé haladva növekszik. Forrás
Tangenciális
Ez a fajta torzítás a gyártás hibáiból adódik, a lencse nem párhuzamos a képalkotóval. Ez a torzítás két paraméterrel ( adható meg. Forrás
Milyen interpolációs technikákat ismer?
Ismertesse a legközelebbi szomszéd, a bilineáris és a biköbös interpolációs technikák alapelvét (képletek nem szükségesek).
Ebben az értelemben az adott mennyiségű képpontból nagyobb (vagy kisebb) felbontású, több (vagy kevesebb) képpontot tartalmazó képet állítunk elő. Motiválhatja például a kép nagyításának igénye. Nagyításnál egyértelműen hiányzó információt pótolunk, kicsinyítéskor viszont a pixelek elhelyezkedésének változása miatt szükséges interpolálni (azonos képtartalmat kevesebb, jellemzően más pozícióba kerülő adatponttal ábrázolunk).
- Legközelebbi szomszéd: A nagyított kép egyes pixeleinek értékeit az alapján határozzuk meg, hogy melyik eredeti pixelhez vannak legközelebb, azzal tesszük őket egyenlővé. Pixeles képet eredményez.
- Bilineáris: Az új pixelek értékét mindkét irányban lineárisan interpoláljuk (név innen), azaz egyenest illesztünk a két közeli eredeti pixel érték közé, és a keresett érték az egyenes pixelnek megfelelő helyén felvett értéke lesz. Az egyenesillesztést tehát a legközelebbi 4 pixel alapján hajtjuk végre. Furcsa artifact-okat tud okozni, viszont nagyon gyors.
- Biköbös (bicubic): Lassabb a bilineárisnál, de szebb eredményt is ad. A legközelebbi 16 pixel alapján számol. Figyelembe veszi a szomszédos pixel értékeket, az x-y irányú deriváltakat és kereszt deriváltakat, az ezekből következő meredekségi kényszerekre felírt egyenleteket oldja meg.
- Lánczos
- Komplex megoldások
- Görbeillesztés
- Fraktál
- Scale2x, 3x, 4x
Mit jelent a képi matematika?
Milyen műveleteket alkalmazhatunk a gyakorlatban?
Adja meg, hogy melyik eljárás milyen feladatra használható.
Képi matematika esetén végezhetünk műveleteket kép-érték vagy kép-kép között.
Lehetséges műveletek
- összeadás/kivonás/átlagolás
- szorzás/osztás/normalizálás
- maximum/minimum
- logikai műveletek (főleg bináris képeknél)
Gyakorlati alkalmazás
- Kép-érték esetben az összeadás fényerő állítást jelent, a szorzás brightness/contrast állítást.[?]
- A szorzás művelet használható textúrázásra (maszkolásra).
- Az összeadás/átlagolás használható zajcsökkentésre.
- A kivonás használható különbségképzésre, a háttér eltávolítására (mozgó/elmozdult objektumok keresésére).