„Algoritmuselmélet - PPZH, 2013.05.23.” változatai közötti eltérés
Új oldal, tartalma: „{{Vissza|Algoritmuselmélet}} == 2013.05.23 - PPZH megoldásai== ===1. Feladat=== TODO {{Rejtett |mutatott=<big>'''Megoldás'''</big> |szöveg= TODO }} ===2. Feladat…” |
|||
| (4 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 2. sor: | 2. sor: | ||
== 2013.05.23 - PPZH megoldásai== | == 2013.05.23 - PPZH megoldásai== | ||
===1. Feladat=== | ===1. Feladat (Van megoldás)=== | ||
Tudjuk, hogy az <math> f(n), g(n) : \textsc{N} \rightarrow \textsc{N} </math> függvényekre igaz, hogy <math> f(n)= \Omega (logn) </math> és <math> g(n) = \Theta (n^4) .</math> | |||
Lehetséges-e, hogy: | |||
'''(a)''' <math> f(n) = \Theta (g(n)) ?</math> | |||
'''(b)''' <math> g(n) = O(f(n)) ?</math> | |||
(Ez két, egymástól függetlenül megválaszolandó kérdés.) | |||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
'''a)''' | |||
*Ha <math> f(n) = n^4 , g(n) = n^4 </math> | |||
*Akkor igaz az, hogy: | |||
**<math> f(n)= \Omega (logn) \Rightarrow n^4 = \Omega (logn)</math> | |||
**És az is, hogy <math> f(n) = \Theta (g(n)) \Rightarrow n^4 = \Theta (n^4)</math> | |||
*Tehát lehetséges. | |||
'''b)''' | |||
*Ha <math> g(n) = n^4 , f(n) = n^4 </math> | |||
*Akkor igaz az, hogy: | |||
**<math> g(n)= \Theta (n^4) \Rightarrow n^4 = \Theta (n^4)</math> | |||
**És az is, hogy <math> g(n) = O(f(n)) \Rightarrow n^4 = O(n^4)</math> | |||
*Tehát lehetséges. | |||
}} | }} | ||
===2. Feladat=== | ===2. Feladat (Van megoldás) === | ||
Távmunkában fogunk dolgozni mostantól n napon át. Nem kell minden nap bejárnunk, de at alábbi három feltételt be kell tartanunk: | |||
* két egymást követő benti munkanap között legfeljebb k nap telhet elm | |||
* az n nap során legfeljebb egyszer maradhatunk pontosan k napig távol, | |||
* az első és a n. napon be kell mennünk. | |||
Sajnos a kék metróval járunk dolgozni, ami hol jár, hol nem, de szerencsére megjósolták nekünk, hogy a kötvetkező n napoban mely napokon lesz üzemzavar, ezeken a napokon nem akarunk dolgozni menni (az első és az utolsó napon nem lesz üzemzavar). | |||
Adjon algoritmust, ami a jóslás eredmények ismeretében O(nk) lépésben meghatározza, hogy legkevesebb hány bemenéssel tudjuk megúszni ezt az n munkanapot. | |||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
A megoldást először a 2. feltétel figyelembevétele nélkül írom le, anélkül sokkal egyszerűbb. | |||
Vegyünk fel egy n méretű tömböt. Ennek az i-edik eleme legyen az a szám, ahány napot muszáj bent lennünk, ha az i. napon be akarunk menni. | |||
Ha az i. napon üzemzavar van, akkor a tömb i-edik eleme legyen végtelen. Ha nincs üzemzavar, akkor legyen a tömb előző legfeljebb k elemének a minimuma plusz egy (amikor az előző k elemet nézzük, ott k-1 kihagyást engedünk meg). | |||
Pl, ha n = 7, k = 3, és a 2. és az 5. napon lesz üzemzavar: | |||
<table> | |||
<tr> | |||
<td>nap</td> | |||
<td>1</td> | |||
<td>2</td> | |||
<td>3</td> | |||
<td>4</td> | |||
<td>5</td> | |||
<td>6</td> | |||
<td>7</td> | |||
</tr> | |||
<tr> | |||
<td>érték</td> | |||
<td>1</td> | |||
<td>végtelen</td> | |||
<td>2</td> | |||
<td>2</td> | |||
<td>3</td> | |||
<td>végtelen</td> | |||
<td>3</td> | |||
</tr> | |||
</table> | |||
A második feltétel figyelembevételéhez egy két soros táblázattá kell bővítenünk a tömböt. A második sorába tároljuk azt, hogy hány napot kötelező bent lennünk, ha az i. napon bent vagyunk, és kihasználjuk azt is, hogy egyszer pontosan k napot is lehetünk távol. | |||
Ennek az értéke vagy végtelen, vagy a minimuma két lehetőségnek: | |||
* Ha most használtuk fel a k napos lógást, akkor k+1 nappal ezelőtti, első sorbeli elem + 1. | |||
* Ha már korábban felhasználtuk a k napos lógást, akkor az előző k napban nézzük a második sor elemeinek a minimumát + 1. | |||
Pl, ha n = 7, k = 2, és az 5. és a 6. napon lesz üzemzavar: | |||
<table> | |||
<tr> | |||
<td>nap</td> | |||
<td>1</td> | |||
<td>2</td> | |||
<td>3</td> | |||
<td>4</td> | |||
<td>5</td> | |||
<td>6</td> | |||
<td>7</td> | |||
</tr> | |||
<tr> | |||
<td>első sor</td> | |||
<td>1</td> | |||
<td>2</td> | |||
<td>2</td> | |||
<td>3</td> | |||
<td>végtelen</td> | |||
<td>végtelen</td> | |||
<td>végtelen</td> | |||
</tr> | |||
<tr> | |||
<td>második sor</td> | |||
<td>1</td> | |||
<td>2</td> | |||
<td>2</td> | |||
<td>2</td> | |||
<td>végtelen</td> | |||
<td>végtelen</td> | |||
<td>4</td> | |||
</tr> | |||
</table> | |||
Az eredmény természetesen a második sor n-edik eleme. Az algoritmus O(n*k) lefut, hiszen 2*n mezőre kell k elem minimumát kiválasztani, ami - feltéve, hogy két elem minimimuma egy lépés - 2*n*k lépést jelent ami = O(n*k) | |||
}} | }} | ||
| 40. sor: | 138. sor: | ||
}} | }} | ||
===5. Feladat=== | ===5. Feladat (Van megoldás)=== | ||
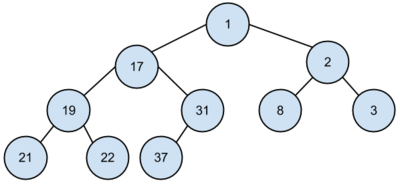
Egy kupac elemeit preorder bejárás szerint kiolvasva az alábbi számsorozatot kapjuk: <math> 1, 17, 19, 21, 22, 31, 37, 2, 8, 3.</math> Rekonstruálható-e ebből a kupac? | |||
{{Rejtett | {{Rejtett | ||
|mutatott=<big>'''Megoldás'''</big> | |mutatott=<big>'''Megoldás'''</big> | ||
|szöveg= | |szöveg= | ||
*A kupac egy teljes bináris fa, így tudjuk, hogy mi a fa alakja. | |||
*Nincs is más dolgunk, mint felrajzolni, majd a preorder bejárás alapján beírni az elemeket a megfelelő csúcsokba, és ellenőrizni, hogy sérül-e valahol a kupac adatszerkezet egy tulajdonsága. | |||
:::::::::::::::::[[File:algel_ppzh_2013tavasz_5_1.png|400px]] | |||
*Látszik, hogy minden rendben van, így a kupac rekonstruálható. | |||
}} | }} | ||
A lap jelenlegi, 2014. május 25., 21:57-kori változata
2013.05.23 - PPZH megoldásai
1. Feladat (Van megoldás)
Tudjuk, hogy az Értelmezés sikertelen (ismeretlen „\textsc” függvény): {\displaystyle f(n), g(n) : \textsc{N} \rightarrow \textsc{N} } függvényekre igaz, hogy és Lehetséges-e, hogy:
(a)
(b)
(Ez két, egymástól függetlenül megválaszolandó kérdés.)
a)
- Ha
- Akkor igaz az, hogy:
- És az is, hogy
- Tehát lehetséges.
b)
- Ha
- Akkor igaz az, hogy:
- És az is, hogy
- Tehát lehetséges.
2. Feladat (Van megoldás)
Távmunkában fogunk dolgozni mostantól n napon át. Nem kell minden nap bejárnunk, de at alábbi három feltételt be kell tartanunk:
- két egymást követő benti munkanap között legfeljebb k nap telhet elm
- az n nap során legfeljebb egyszer maradhatunk pontosan k napig távol,
- az első és a n. napon be kell mennünk.
Sajnos a kék metróval járunk dolgozni, ami hol jár, hol nem, de szerencsére megjósolták nekünk, hogy a kötvetkező n napoban mely napokon lesz üzemzavar, ezeken a napokon nem akarunk dolgozni menni (az első és az utolsó napon nem lesz üzemzavar). Adjon algoritmust, ami a jóslás eredmények ismeretében O(nk) lépésben meghatározza, hogy legkevesebb hány bemenéssel tudjuk megúszni ezt az n munkanapot.
A megoldást először a 2. feltétel figyelembevétele nélkül írom le, anélkül sokkal egyszerűbb.
Vegyünk fel egy n méretű tömböt. Ennek az i-edik eleme legyen az a szám, ahány napot muszáj bent lennünk, ha az i. napon be akarunk menni.
Ha az i. napon üzemzavar van, akkor a tömb i-edik eleme legyen végtelen. Ha nincs üzemzavar, akkor legyen a tömb előző legfeljebb k elemének a minimuma plusz egy (amikor az előző k elemet nézzük, ott k-1 kihagyást engedünk meg).
Pl, ha n = 7, k = 3, és a 2. és az 5. napon lesz üzemzavar:
| nap | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| érték | 1 | végtelen | 2 | 2 | 3 | végtelen | 3 |
A második feltétel figyelembevételéhez egy két soros táblázattá kell bővítenünk a tömböt. A második sorába tároljuk azt, hogy hány napot kötelező bent lennünk, ha az i. napon bent vagyunk, és kihasználjuk azt is, hogy egyszer pontosan k napot is lehetünk távol. Ennek az értéke vagy végtelen, vagy a minimuma két lehetőségnek:
- Ha most használtuk fel a k napos lógást, akkor k+1 nappal ezelőtti, első sorbeli elem + 1.
- Ha már korábban felhasználtuk a k napos lógást, akkor az előző k napban nézzük a második sor elemeinek a minimumát + 1.
Pl, ha n = 7, k = 2, és az 5. és a 6. napon lesz üzemzavar:
| nap | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| első sor | 1 | 2 | 2 | 3 | végtelen | végtelen | végtelen |
| második sor | 1 | 2 | 2 | 2 | végtelen | végtelen | 4 |
3. Feladat
TODO
4. Feladat
TODO
5. Feladat (Van megoldás)
Egy kupac elemeit preorder bejárás szerint kiolvasva az alábbi számsorozatot kapjuk: Rekonstruálható-e ebből a kupac?
- A kupac egy teljes bináris fa, így tudjuk, hogy mi a fa alakja.
- Nincs is más dolgunk, mint felrajzolni, majd a preorder bejárás alapján beírni az elemeket a megfelelő csúcsokba, és ellenőrizni, hogy sérül-e valahol a kupac adatszerkezet egy tulajdonsága.
- Látszik, hogy minden rendben van, így a kupac rekonstruálható.
6. Feladat
TODO
7. Feladat
TODO
8. Feladat
TODO