„Fizika1 vizsga 2009.06.10.” változatai közötti eltérés
A VIK Wikiből
a Kategóriabesorolás |
|||
| (Egy közbenső módosítás, amit egy másik szerkesztő végzett, nincs mutatva) | |||
| 64. sor: | 64. sor: | ||
==Feladatok== | ==Feladatok== | ||
A feladatok [[Media:Fizika1i_vizsga-2009-06-10_1.jpg| scannelt változata]]. | |||
;1. Egy gépkocsi 200m sugarú, vízszintes körpályán mozog. Amikor a sebesség nagysága 10 m/s, a gyorsulás-vektor 120°-os szöget zár be a sebességvektorral. Ekkor a tangenciális gyorsulás nagysága: | ;1. Egy gépkocsi 200m sugarú, vízszintes körpályán mozog. Amikor a sebesség nagysága 10 m/s, a gyorsulás-vektor 120°-os szöget zár be a sebességvektorral. Ekkor a tangenciális gyorsulás nagysága: | ||
| 138. sor: | 139. sor: | ||
<br /> | <br /> | ||
-- [[Lord_Viktor|Lord Viktor]] - 2013.01.25. | -- [[Lord_Viktor|Lord Viktor]] - 2013.01.25. | ||
[[Category:Infoalap]] | |||
A lap jelenlegi, 2013. február 8., 22:37-kori változata
Ez egy eltérő stílusú vizsga volt, a pontozási rendszere ismeretlen. Már nem ilyen stílusúak a vizsgák, de felkészüléshez ideális.
Kiegészítendő mondatok
A feladatok scannelt változata.
- Ha egy részecske helye x(t)= 4 + t2 + t3, átlaggyorsulása 1 és 3 s között ........................................................
- Ha a gravitációs erővonalakkal ellentétel irányban mozdul el egy tömegpont, akkor potenciális energiája ........................................................
- Anyagi pontrendszer eredő impulzusát a belső erők ........................................................
- Egymással párhuzamos tengelyekre számított tehetetlenségi nyomatékok közül az a legkisebb, amelyik esetén a tengely ........................................................
- Gravitációs (centrális) erőtérben mozgó bolygó helyzeti és kinetikus energiáinak összegének előjele ........................................................
- Centrális erőtérben mozgó test energiája és ....................................................... a mozgás során állandó.
- Az északi féltekén szabadon eső test ...................................................... felé térül el.
- Adott frekvenciájú harmonikus rezgőmozgás amplitúdóját és kezdőfázisát a ...................................................... határozzák meg.
- Egy csillapított, gerjesztett oszcillátor frekvenciáját a ...................................................... határozza meg.
- Egy harmonikus hullám sebessége a(z) ...................................................... képlettel számítható ki.
- 101 Hz és 99 Hz frekvenciájú hanghullámokkal lebegést hozunk létre. A lebegés frekvenciája ...................................................... Hz.
- Reverzibilis körfolyamat során az entrópia változás ......................................................
- Adiabatikus állapotváltozás során a gáz által végzett munka ...................................................... megváltozásával egyenlő.
- Ha egy töltött síkkondenzátor lemezei közé dielektrikumot helyezünk, akkor a lemezek közötti feszültség ......................................................
- Elektrosztatikus térben az elektromos térerősség tetszőleges zárt görbére vett integráljának értéke ......................................................
Megoldás
- 14 km/s2
- nő
- nem befolyásolják
- a tömegközépponton megy át
- ?
- impulzusmomentuma
- kelet
- kezdőfeltételek
- gerjedés frekvenciája
- v= ω/k
- 2
- zérus
- a belső energia negatív
- csökken
- zérus
Kifejtős kérdések
A feladatok scannelt változata: 1-2.feladat, 3-4. feladat.
Max. 12 pont, feladatonként 3 pont
- 1.
- a. Írja fel pontrendszerre az impulzustételt!(1p)
- b. Mi a tömegközéppont definíciója?( 1p)
- c. Mit állít a tömegközéppont-tétel? (1p)
- 2.
- a. Adja meg a tehetetlenségi nyomaték definícióját! (1p)
- b. Mit mond ki a Steiner-tétel (párhuzamos tengelyek tétele)? (1p)
- c. Írja fel rögzített tengely körül forgó merev test mozgásegyenletét! (1p)
- 3.
- a. Mi az entrópia infinitezimális megváltozásának definíciója a termodinamikában? (1p)
- b. Hogyan számíthatjuk ideális gáz tetszőleges reverzibilis állapotváltozásra az entrópia megváltozását? (1p)
- c. Irreverzibilis folyamatoknál (pl. hőmérséklet-kiegyenlítődés) hogyan változik az univerzum entrópiája? (1p)
- 4.
- a. Írja fel az elektromos potenciálkülönbség definícióját! (1p)
- b. Írja fel az elektromos potenciál definícióját! (1p)
- c. Az elektromos potenciál ismeretében hogyan számíthatjuk ki a térerősséget? (1p)
- 5.
- a. Írja fel az elektrosztatika Gauss-tételét vákuumban! (1p)
- b. Az elektrosztatika Gauss-tételének felhasználásával határozza meg egy Q töltéssel rendelkező fémgömb elektromos terét a gömbön kívül! Késítsen magyarázó rajzot! (2p)
Feladatok
A feladatok scannelt változata.
- 1. Egy gépkocsi 200m sugarú, vízszintes körpályán mozog. Amikor a sebesség nagysága 10 m/s, a gyorsulás-vektor 120°-os szöget zár be a sebességvektorral. Ekkor a tangenciális gyorsulás nagysága
- A: 0,14 m/s2
- B: 0,29 m/s2
- C: 0,58 m/s2
- D: 1,2 m/s2
- E: egyik sem
- 2. Az x tengely mentén mozgó anyagi pontra Fx= (2x + 4) N erő hat. Miközben a test az x= 2 m pontból az x= 5 m pontba jut, kinetikus energiájának megváltozása
- A: 40 J
- B: 33 J
- C: 26 J
- D: 20 J
- E: egyik sem
- 3. Északi 30° szélességi körön nyugat felé v sebességgel haladó testre ható Coriolis-erő függőleges komponense
- A: 31/2 mvω felfelé
- B: 31/2 mvω lefelé
- C: mvω felfelé
- D: mvω lefelé
- E: egyik sem
- 4. Az r= (ex + ey) m helyvektorú részecskére F= (2ex + 3ey) N erő hat. Az erő origóra számított forgatónyomatéka
- A: 1 ez Nm
- B: 5 ez Nm
- C: -1 ez Nm
- D: -5 ez Nm
- 5. Egy 3m tömegű tömör, állandó ω szögsebességgel forgó tárcsát ráejtjük az alatta lévő álló m tömegű, azonos R sugarú, közös függőleges tengelyű, tömör tárcsára. Mekkora lesz a közös szögsebesség? (ITKP= mR2/2)
- A: 1/4 ω
- B: 1/3 ω
- C: 1/2 ω
- D: 3/4 ω
- E: egyik sem
- 6. Egy síklapon egy test nyugszik, a tapadási surlódási tényező 0,5. A lapot 5 cm amplitúdóval (vízszintesen) rázzuk. Mekkora a rázás periódusideje, ha a test éppen nem csúszik meg a lapon?
- A: 0,63 s
- B: 1,3 s
- C: 2s
- D: 3,9 s
- E: egyik sem
- 7. Egy személygépkocsi 126 km/h sebességgel közeledik egy álló, szirénázó rendőrautóhoz. Milyen frekvenciájúnak hallja az 500 Hz-es szirénát, ha a hangsebesség a levegőben 340 m/s?
- A: 453 Hz
- B: 448 Hz
- C: 557 Hz
- D: 551 Hz
- E: egyik sem
- 8. Egyatomos ideális gázt adiabatikus állapotváltozás során térfogatának nyolcadrészére összenyomunk. Hányszorosára változott a nyomása?
- A: 8
- B: 18,4
- C: 32,2
- D: 64
- E: egyik sem
- 9. A tér egy tartományában az elektromos térerősség E= (-3x ex + 4 ez) N/C. Az A és B pontok az x tengelyen vannak. xA= 3m és xB= 5m. Az UB - UA potenciálkülönbség
- A: -24 V
- B: 24 V
- C: -18 V
- D: 30 V
- E: egyik sem
- 10. 0,1 m sugarú vezető gomb felületén az elektromos térerősség 10 kV/m. A végtelen távoli ponthoz képest mekkora az elektromos potenciál a gömb középpontjában?
- A: 0
- B: 100 V
- C: 1 kV
- D: 10 kV
- E: egyik sem
Megoldás
non-official
1 2 3 4 5 6 7 8 9 10 B B B A D A D C B C
A számolós feladatok megoldása:
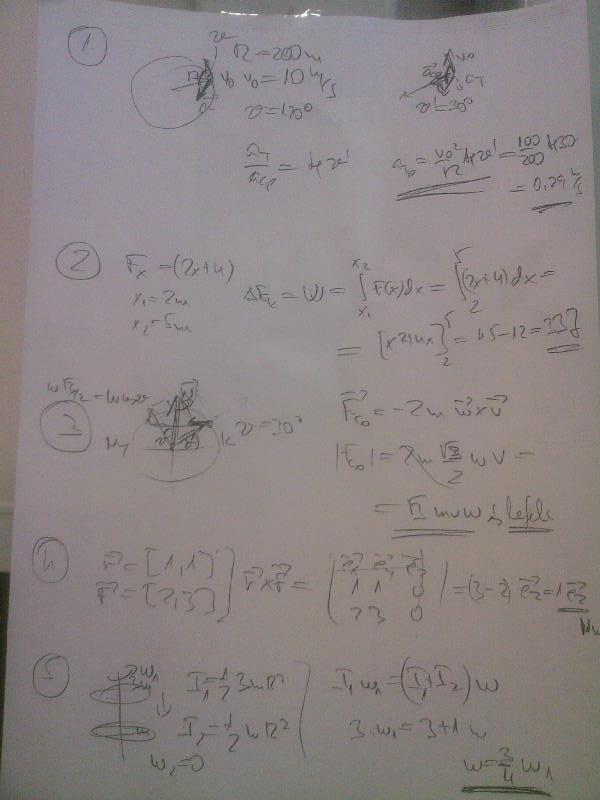

-- Lord Viktor - 2013.01.25.
