„Laboratórium 1 - 2006 őszi ZH megoldások” változatai közötti eltérés
Új oldal, tartalma: „{{GlobalTemplate|Villanyalap|LaborI2006ZH}} ==Labor 1. - 2006ZH== =====1. Időben periodikusan változó jelek esetén definiálja a következő jellemzőket===== * …” |
a autoedit v2: fájlhivatkozások egységesítése, az új közvetlenül az adott fájlra mutat |
||
| (4 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
== 1. Feladat == | |||
'''Időben periodikusan változó jelek esetén definiálja a következő jellemzőket:''' | |||
'''a) Egyszerű középérték:''' | |||
<math> U_0=\frac{1}{T}\int_0^Tu(t)dt</math> | <math> U_0=\frac{1}{T}\int_0^Tu(t)dt</math> | ||
'''b) Abszolút középérték:''' | |||
<math> U_k=\frac{1}{T}\int_0^T \left| u(t) \right| dt</math> | <math> U_k=\frac{1}{T}\int_0^T \left| u(t) \right| dt</math> | ||
'''c) Effektív érték:''' | |||
<math> U=\sqrt{\frac{1}{T}\int_0^T(u(t))^2dt}</math> | <math> U=\sqrt{\frac{1}{T}\int_0^T(u(t))^2dt}</math> | ||
'''d) Csúcstényező:''' | |||
<math> k_{cs}=\frac{U_{csucs}}{U} | |||
<math> k_{cs}=\frac{U_{csucs}}{U} </math> | |||
'''e) Formatényező:''' | |||
<math> k_f=\frac{U}{U_k} </math> | |||
== 2. Feladat == | |||
'''Egy hosszú koaxiális kábel hibájának helyét szeretnénk meghatározni reflexióméréssel az időtartományban. Ennek érdekében ugrásjelet adunk egy soros ellenálláson keresztül a kábelre. A soros ellenállás értéke megegyezik a kábel hullámimpedanciájával, a generátor kimeneti ellenállását elhanyagoljuk.''' | |||
'''a) Rajzolja fel, hogy milyen jelalak mérhető a kábel bemenetén, ha a hibahelyen a lezárás <math> Z_L=3Z_0 </math>-val modellezhető!''' | |||
A lépésfüggvény megjelenésekor az energiamentes tápvonal bemenete <math>Z_0</math> impedanciát mutat függetlenül a terheléstől, így le kell osztani a feszültséget a <math>R_s</math> soros ellenállás és a <math>Z_0</math> hullámimpedancia között, ez kerül rá a bemenetre. | A lépésfüggvény megjelenésekor az energiamentes tápvonal bemenete <math>Z_0</math> impedanciát mutat függetlenül a terheléstől, így le kell osztani a feszültséget a <math>R_s</math> soros ellenállás és a <math>Z_0</math> hullámimpedancia között, ez kerül rá a bemenetre. | ||
[[File:Labor1 kép5.gif]] | |||
'''b) Jelölje be a releváns időintervallumokat (<math> T_k </math> az egyirányú út megtételéhez szükséges idő), az amplitúdókat (<math> U_1 </math> a generátor ugrásjelének nagysága)!''' | |||
'''c) Mekkora a reflexiós tényező?''' | |||
<math> \gamma = \frac{E_r}{E_i}=\frac{Z_L-Z_0}{Z_L+Z_0}= \frac{1}{2} </math> | <math> \gamma = \frac{E_r}{E_i}=\frac{Z_L-Z_0}{Z_L+Z_0}= \frac{1}{2} </math> | ||
==== | == 3. Feladat == | ||
'''Szinusz generátor torzítását mérjük oszcilloszkóp FFT funkciójával. A generátor beállított paraméterei: <math> U_{pp} = 1V </math>, nagyimpedanciás kimenet. Az oszcilloszkópot torzításmentesnek vesszük. Két minta figyelhető meg: 100Hz illetve 300Hz frekvencián, -9dBV és -49dBV nagysággal.''' | |||
'''a) Mekkora effetív értékű és frekvenciájú a bemenő jel?''' | |||
<math> U = \frac{1}{2} \frac{ 1 }{ \sqrt{2} } </math> | <math> U = \frac{1}{2} \frac{ 1 }{ \sqrt{2} } </math> | ||
'''b) A torzítás megadására használt két kifejezés?''' | |||
<math> k_1=\sqrt{\frac{ \sum_{i=2}^{\infty}X_i^2}{\sum_{i=1}^{\infty}X_i^2} } </math> | <math> k_1=\sqrt{\frac{ \sum_{i=2}^{\infty}X_i^2}{\sum_{i=1}^{\infty}X_i^2} } </math> | ||
<math> k_2=\sqrt{ \frac{ \sum_{i=2}^{\infty}X_i^2}{X_1^2} } </math> | <math> k_2=\sqrt{ \frac{ \sum_{i=2}^{\infty}X_i^2}{X_1^2} } </math> | ||
'''c) Adja meg a generátor torzítását százalékban az egyszerűbb kifejezéssel!''' | |||
== | <math>X_1=10^{-9/20}=0,35V</math> | ||
{ | <math>X_2=10^{-49/20}=0,0035V</math> | ||
|Z=0, ha | |||
Ennek megfelelően: <math> k_2=\sqrt{ \frac{ 0,0035^2}{0,35^2 }}=0,01 </math> azaz 1% | |||
== 4. Feladat == | |||
'''Egy ismeretlen felépítésű kétpólus impedanciáját mérjük a frekvencia függvényében. A kapott impedanciagörbe sáváteresztő jellegű, azaz:''' | |||
<math> |Z|=0, ha f\Rightarrow 0</math> | |||
<math> |Z|=0, ha f\Rightarrow \infty </math> | |||
<math> |Z|= Z_m, ha f=f_m </math> | |||
| | |||
Adja meg a legvalósághűbb 3 elemű modellt, és a modellparaméterek kapcsolatát <math>Z_m</math> és <math>f_m</math> paraméterrel! | '''Adja meg a legvalósághűbb 3 elemű modellt, és a modellparaméterek kapcsolatát <math>Z_m</math> és <math>f_m</math> paraméterrel!''' | ||
Mivel DC-n és nagyfrekvencián is nulla az impedancia, ezért a legjobb modell a párhuzamos LC lenne, de a rezonancián végtelen az impedanciája. Ezért a megoldás párhuzamos RLC. | Mivel DC-n és nagyfrekvencián is nulla az impedancia, ezért a legjobb modell a párhuzamos LC lenne, de a rezonancián végtelen az impedanciája. Ezért a megoldás párhuzamos RLC. | ||
Modellparaméterek közötti összefüggés: <math> |Z_m|=R </math> | Modellparaméterek közötti összefüggés: <math> |Z_m|=R </math> | ||
Illetve rezonancián: <math> f_m=\frac{1}{2\pi \sqrt{LC}}</math> | Illetve rezonancián: <math> f_m=\frac{1}{2\pi \sqrt{LC}}</math> | ||
Így DC-n a tekercs miatt rövidzár. | |||
A f=végtelen frekvencián a kondi miatt rövidzár. | |||
== 5. Feladat == | |||
'''Adott egy torroid tekercs. N=140, mért értékei: L=50mH, menetkapacitás: C=300pF.''' | |||
'''a)Az <math> A_L </math> meghatározása:''' | |||
<math> A_L = \frac{L}{N^2} = 2551 nH </math> | <math> A_L = \frac{L}{N^2} = 2551 nH </math> | ||
'''b) Milyen frekvenciasávban kisebb 0,5%-nál a menetkapacitásból adódó hiba?''' | |||
<math> L_{eff}=\frac{L_0}{1-(\frac{\omega}{{\omega}_r})^2}</math> | <math> L_{eff}=\frac{L_0}{1-(\frac{\omega}{{\omega}_r})^2}</math> | ||
<math> (\frac{\omega}{{\omega}_r})^2=0,005</math> esetén | <math> (\frac{\omega}{{\omega}_r})^2=0,005</math> esetén | ||
<math> L_{eff}=L_0 \cdot 1,005</math>, | |||
azaz | <math> L_{eff}=L_0 \cdot 1,005</math>, azaz 5%-os a növekedés. | ||
<math> \frac{\omega}{{\omega}_r}=0,0707</math> | <math> \frac{\omega}{{\omega}_r}=0,0707</math> | ||
<math> \omega \leq 0,0707{\omega}_r =0,0707\frac{1}{\sqrt{LC}}=18,25 \cdot 10^3\frac{rad}{s}\] \[ f \leq 2,9kHz</math> | <math> \omega \leq 0,0707{\omega}_r =0,0707\frac{1}{\sqrt{LC}}=18,25 \cdot 10^3\frac{rad}{s}\] \[ f \leq 2,9kHz</math> | ||
==== | == 6. Feladat == | ||
'''Adjon mérési elrendezést bipoláris tranzisztor h21 paraméterének mérésére, és röviden írja le a mérés menetét!''' | |||
[[File:Labor1 kép6.gif]] | |||
A mérőkapcsolásban árammérővel mérjük <math> I_B </math> bázisáramot és <math> I_C </math> kollektor áramot. VÁltoztassuk <math> U_B </math> és <math> U_{CE} = U_{tap}</math> feszültségeket. <math>R_s=100 k\Omega </math> -os ellenállással biztosítjuk az áramgenerátoros meghajtást. | A mérőkapcsolásban árammérővel mérjük <math> I_B </math> bázisáramot és <math> I_C </math> kollektor áramot. VÁltoztassuk <math> U_B </math> és <math> U_{CE} = U_{tap}</math> feszültségeket. <math>R_s=100 k\Omega </math> -os ellenállással biztosítjuk az áramgenerátoros meghajtást. | ||
| 79. sor: | 113. sor: | ||
<math> \beta = h_{21}=\frac{\Delta I_c}{\Delta I_B} (U_{CE}=</math>állandó) | <math> \beta = h_{21}=\frac{\Delta I_c}{\Delta I_B} (U_{CE}=</math>állandó) | ||
[[File:Labor1 kép7.gif]] | |||
== 7. Feladat == | |||
'''TTL inverter transzfer karakterisztikáját kell megmérnie:''' | |||
'''a) Milyen gerjesztést alkalmazna?''' | |||
* Mindenképpen olyat ami minden időpillanatban pozitív értéket vesz föl, ugyanis a TTL áramkörök levágják a negatív részét a jelnek. | * Mindenképpen olyat ami minden időpillanatban pozitív értéket vesz föl, ugyanis a TTL áramkörök levágják a negatív részét a jelnek. | ||
* Szimmetrikus háromszögjel jó választás lehet, mert így jól megfigyelhető a komparálási szint, mert nincsenek benne hirtelen ugrások. | * Szimmetrikus háromszögjel jó választás lehet, mert így jól megfigyelhető a komparálási szint, mert nincsenek benne hirtelen ugrások. | ||
| 89. sor: | 126. sor: | ||
* Mérésen: 350Hz-es 0 és 5V közötti szimmetrikus háromszögjellel mértük. | * Mérésen: 350Hz-es 0 és 5V közötti szimmetrikus háromszögjellel mértük. | ||
'''b) Ábrázolja közös ábrán a gerjesztő jelet és a választ! Ügyeljen a tengelyek skálázására!''' | |||
[[File:Labor1 kép8.bmp]] | |||
== 8. Feladat == | |||
'''Van egy 4bites szinkron számlálónk, mely névlegesen 40MHz frekvencián képes üzemelni. Szeretnénk megmérni, meddig növelhető ez a működési frekvencia. Ehhez adott egy négyszögjel generátor (1Hz-200MHz), valamint egy logikai analizátor. Röviden írja le, hogyan végezné el a mérést!''' | |||
A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. A végállapotot (1111) állítjuk be leállási feltételként. 40MHz-től növekvő frekvenciákon ellenőrizzük, hogy a számláló egymást követő állapotai megfelelnek-e a bináris számláló működésének. A legalacsonyabb olyan frekvencia ahol még igen, a maximális működési frekvencia. | A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. A végállapotot (1111) állítjuk be leállási feltételként. 40MHz-től növekvő frekvenciákon ellenőrizzük, hogy a számláló egymást követő állapotai megfelelnek-e a bináris számláló működésének. A legalacsonyabb olyan frekvencia ahol még igen, a maximális működési frekvencia. | ||
== 9. Feladat == | |||
'''Tételezze fel, hogy egy soros adó képes egy karaktersorozat folytonos, szünet nélküli kiadására! Ha az átviteli mód paraméterei 8 adatbit, 1 paritásbit és 2 STOP bit 9600 bit/s átviteli sebesség mellett, akkor az Ön NEPTUN-kódjának az átvitele mennyi ideig tart?''' | |||
9600bps esetén a bitidő 104,167 <math> \mu </math> s. | 9600bps esetén a bitidő 104,167 <math> \mu </math> s. | ||
Az átviteli mód 1START + 8 adat + 1 PAR + 2 STOP = 12bit/karakter keretet határoz meg. | Az átviteli mód 1START + 8 adat + 1 PAR + 2 STOP = 12bit/karakter keretet határoz meg. | ||
Egy karakter átvitele <math> 12 \cdot 104,167 = 1,25</math>ms | Egy karakter átvitele <math> 12 \cdot 104,167 = 1,25</math>ms | ||
Neptun kód 6 karakter, így <math> 6 \cdot 1,25 </math>ms = 7,5 ms | Neptun kód 6 karakter, így <math> 6 \cdot 1,25 </math>ms = 7,5 ms | ||
== 10. Feladat == | |||
'''Adjon tesztvektort, mely az automata összes állapotátmenetét teszteli!''' | |||
{| border="1" | {| border="1" | ||
| 118. sor: | 161. sor: | ||
| C || B/0 || C/0 | | C || B/0 || C/0 | ||
|} | |} | ||
{| border="1" | {| border="1" | ||
| 126. sor: | 170. sor: | ||
| állapot || A || B || B || C || C || B || A || C | | állapot || A || B || B || C || C || B || A || C | ||
|} | |} | ||
Több jó megoldás is lehetséges! | |||
[[Kategória:Villamosmérnök]] | |||
A lap jelenlegi, 2017. július 12., 15:15-kori változata
1. Feladat
Időben periodikusan változó jelek esetén definiálja a következő jellemzőket:
a) Egyszerű középérték:
b) Abszolút középérték:
c) Effektív érték:
d) Csúcstényező:
e) Formatényező:
2. Feladat
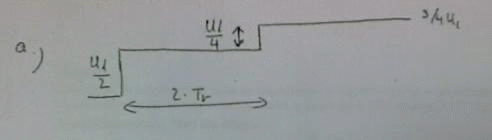
Egy hosszú koaxiális kábel hibájának helyét szeretnénk meghatározni reflexióméréssel az időtartományban. Ennek érdekében ugrásjelet adunk egy soros ellenálláson keresztül a kábelre. A soros ellenállás értéke megegyezik a kábel hullámimpedanciájával, a generátor kimeneti ellenállását elhanyagoljuk.
a) Rajzolja fel, hogy milyen jelalak mérhető a kábel bemenetén, ha a hibahelyen a lezárás -val modellezhető!
A lépésfüggvény megjelenésekor az energiamentes tápvonal bemenete impedanciát mutat függetlenül a terheléstől, így le kell osztani a feszültséget a soros ellenállás és a hullámimpedancia között, ez kerül rá a bemenetre.
b) Jelölje be a releváns időintervallumokat ( az egyirányú út megtételéhez szükséges idő), az amplitúdókat ( a generátor ugrásjelének nagysága)!
c) Mekkora a reflexiós tényező?
3. Feladat
Szinusz generátor torzítását mérjük oszcilloszkóp FFT funkciójával. A generátor beállított paraméterei: , nagyimpedanciás kimenet. Az oszcilloszkópot torzításmentesnek vesszük. Két minta figyelhető meg: 100Hz illetve 300Hz frekvencián, -9dBV és -49dBV nagysággal.
a) Mekkora effetív értékű és frekvenciájú a bemenő jel?
b) A torzítás megadására használt két kifejezés?
c) Adja meg a generátor torzítását százalékban az egyszerűbb kifejezéssel!
Ennek megfelelően: azaz 1%
4. Feladat
Egy ismeretlen felépítésű kétpólus impedanciáját mérjük a frekvencia függvényében. A kapott impedanciagörbe sáváteresztő jellegű, azaz:
Adja meg a legvalósághűbb 3 elemű modellt, és a modellparaméterek kapcsolatát és paraméterrel!
Mivel DC-n és nagyfrekvencián is nulla az impedancia, ezért a legjobb modell a párhuzamos LC lenne, de a rezonancián végtelen az impedanciája. Ezért a megoldás párhuzamos RLC.
Modellparaméterek közötti összefüggés:
Illetve rezonancián:
Így DC-n a tekercs miatt rövidzár.
A f=végtelen frekvencián a kondi miatt rövidzár.
5. Feladat
Adott egy torroid tekercs. N=140, mért értékei: L=50mH, menetkapacitás: C=300pF.
a)Az meghatározása:
b) Milyen frekvenciasávban kisebb 0,5%-nál a menetkapacitásból adódó hiba?
esetén
, azaz 5%-os a növekedés.
Értelmezés sikertelen (formai hiba): {\displaystyle \omega \leq 0,0707{\omega}_r =0,0707\frac{1}{\sqrt{LC}}=18,25 \cdot 10^3\frac{rad}{s}\] \[ f \leq 2,9kHz}
6. Feladat
Adjon mérési elrendezést bipoláris tranzisztor h21 paraméterének mérésére, és röviden írja le a mérés menetét!
A mérőkapcsolásban árammérővel mérjük bázisáramot és kollektor áramot. VÁltoztassuk és feszültségeket. -os ellenállással biztosítjuk az áramgenerátoros meghajtást.
állandó)
7. Feladat
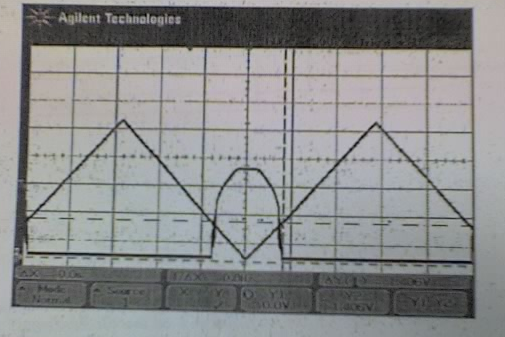
TTL inverter transzfer karakterisztikáját kell megmérnie:
a) Milyen gerjesztést alkalmazna?
- Mindenképpen olyat ami minden időpillanatban pozitív értéket vesz föl, ugyanis a TTL áramkörök levágják a negatív részét a jelnek.
- Szimmetrikus háromszögjel jó választás lehet, mert így jól megfigyelhető a komparálási szint, mert nincsenek benne hirtelen ugrások.
- Nem szabad nagyfrekvenciás jelnek lennie, ne legyen összemérhető a késleltetési időkkel. (?)
- Mérésen: 350Hz-es 0 és 5V közötti szimmetrikus háromszögjellel mértük.
b) Ábrázolja közös ábrán a gerjesztő jelet és a választ! Ügyeljen a tengelyek skálázására!
8. Feladat
Van egy 4bites szinkron számlálónk, mely névlegesen 40MHz frekvencián képes üzemelni. Szeretnénk megmérni, meddig növelhető ez a működési frekvencia. Ehhez adott egy négyszögjel generátor (1Hz-200MHz), valamint egy logikai analizátor. Röviden írja le, hogyan végezné el a mérést!
A logikai analizátor adat bemeneteire csatlakoztatjuk a számláló kimeneteit. Állapotanalízis üzemmódot állítunk be, a számláló órajele a mintavevő órajel. A végállapotot (1111) állítjuk be leállási feltételként. 40MHz-től növekvő frekvenciákon ellenőrizzük, hogy a számláló egymást követő állapotai megfelelnek-e a bináris számláló működésének. A legalacsonyabb olyan frekvencia ahol még igen, a maximális működési frekvencia.
9. Feladat
Tételezze fel, hogy egy soros adó képes egy karaktersorozat folytonos, szünet nélküli kiadására! Ha az átviteli mód paraméterei 8 adatbit, 1 paritásbit és 2 STOP bit 9600 bit/s átviteli sebesség mellett, akkor az Ön NEPTUN-kódjának az átvitele mennyi ideig tart?
9600bps esetén a bitidő 104,167 s.
Az átviteli mód 1START + 8 adat + 1 PAR + 2 STOP = 12bit/karakter keretet határoz meg.
Egy karakter átvitele ms
Neptun kód 6 karakter, így ms = 7,5 ms
10. Feladat
Adjon tesztvektort, mely az automata összes állapotátmenetét teszteli!
| X | 0 | 1 |
| A | C/0 | B/0 |
| B | C/1 | B/1 |
| C | B/0 | C/0 |
| RESET | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| X | - | 1 | 1 | 0 | 1 | 0 | - | 0 |
| állapot | A | B | B | C | C | B | A | C |
Több jó megoldás is lehetséges!