„Laboratórium 2 - 4. Mérés ellenőrző kérdései” változatai közötti eltérés
Új oldal, tartalma: „{{GlobalTemplate|Villanyalap|Labor2Kerdes4}} vissza a Labor 2. tárgyhoz <br/> ---- ====1. Hogyan számoljuk ki a pillanatnyi teljesítményt?==== A pil…” |
|||
| (23 közbenső módosítás, amit 4 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
{{ | {{Vissza|Laboratórium 2}} | ||
{{Vissza|Laboratórium 2 - 4. Mérés: Villamos teljesítmény mérése}} | |||
<div class="noautonum">__TOC__</div> | |||
==1. Hogyan számoljuk ki a pillanatnyi teljesítményt?== | |||
A pillanatnyi teljesítmény az áram és feszültség pillanatértékeinek szorzata: <math> p(t)=u(t)i(t) </math> | |||
Ha tudjuk, hogy a feszültségünk és az áramunk időfüggvénye is szinuszos, azaz: | |||
<math>u(t) = U \cdot \cos ( \omega t + \rho )</math> | |||
<math>i(t) = I \cdot \cos ( \omega t + \rho - \varphi )</math> | |||
Ahol <math>\varphi</math> a feszültség és az áram közötti fáziskülönbség, <math> \rho</math> pedig a kezdőfázis. | |||
====7. Milyen megvalósítási lehetőségei vannak két villamos | <math>p(t) = {1 \over 2} UI \cos(\varphi) + {1 \over 2} UI \cos( 2 \omega t + 2 \rho - \varphi)</math> | ||
Felhasználva a hatásos és a meddő teljesítmény képletét: | |||
<math>P={1 \over 2} UI \cos(\varphi)=U_{eff}I_{eff} \cos(\varphi )</math> | |||
<math>Q={1 \over 2} UI \sin(\varphi)= U_{eff}I_{eff} \sin(\varphi )</math> | |||
A pillanatnyi teljesítmény az alábbi alakban is felírható: | |||
<math>p(t) = P \cdot \left[ 1 + \cos( 2 \omega t + 2 \varphi ) \right]\; + \; Q \cdot \sin( 2 \omega t + 2 \varphi )</math> | |||
==2. Megállapodás szerint mit jelent az egyenáramú teljesítmény pozitív vagy negatív előjele?== | |||
Ez attól függ, hogy ki kérdezi. Ha egy egyszerű halandó, akkor a pozitív előjel a fogyasztói, negatív a termelői teljesítményt jelenti. Legyen ez most a helyes válasz. | |||
Ha pedig egy VET-es kollega, akkor rá kell kérdezni, hogy milyen irányrendszerben gondolja, mert a fogyasztó irányrendszerben ohmos és induktív jellegű fogyasztó által felvett hatásos és meddő teljesítmény is pozitív (ahogy az előbb), de ugyanígy a tipikus fogyasztót tápláló generátornak is pozitív mind a hatásos, mind pedig a meddő teljesítménye a generátoros pozitív irányrendszerben. | |||
[[File:teljesitmenyek_tablazat.JPG|500px]] | |||
==3. Hogyan számítható ki a két-pólus hatásos, meddő és látszólagos teljesítménye?== | |||
'''Feladat:''' Egy váltakozó áramú áramkörben valamely két-póluson mért feszültség és áram '''effektív értéke''' <math>U</math>, illetve <math>I</math>. a feszültség és az áram közötti fázisszög <math>\varphi</math> (a feszültség siet az áramhoz képest, ha <math>\varphi</math> pozitív). Hogyan számítható ki a két-pólus hatásos, meddő és látszólagos teljesítménye? Hogyan változnak ezek az értékek, ha a <math>\varphi</math> fázisszög előjelet vált? | |||
'''Megoldás:''' | |||
Látszólagos teljesítmény <math>[VA]</math> | |||
<math>S= UI = \sqrt{P^2 + Q^2} </math> | |||
Hatásos teljesítmény <math>[W]</math> | |||
<math>P= Re \left\{ S \right\} = UI \cdot \cos( \varphi ) </math> | |||
Meddő teljesítmény <math>[Var]</math> | |||
<math>Q= Im \left\{ S \right\} = UI \cdot \sin( \varphi ) </math> | |||
Ezek közül csak a meddő teljesítmény előjele változik, ugyanis csak az érzékeny a <math>\varphi</math> előjelére, mivel a koszinusz páros függvény. | |||
==4. Hogyan definiáljuk a hatásos és meddő teljesítményt, ha periodikus, de nem szinuszos jelekről van szó?== | |||
'''Feladat:''' Legyen <math>U_0</math> és <math>I_0</math> a feszültség és az áram egyenáramú összetevője, <math>U_i</math> és <math>I_i</math> a feszültség, illetve az áram i-edik felharmonikusának effektív értéke és <math>\varphi_i</math> ezen felharmonikusok közti fázisszög (a feszültség siet az áramhoz képest, ha <math>\varphi</math> pozitív). | |||
'''Megoldás:''' | |||
Ilyenkor csak az azonos frekvenciájú összetevők hoznak létre teljesítményt! | |||
Hatásos teljesítmény: | |||
<math>P=U_0 I_0+ \sum_{i=1}^{\infty} U_i I_i \cdot \cos( \varphi)</math> | |||
Meddő teljesítmény: | |||
<math>Q= \sum_{i=1}^{\infty} U_i I_i \cdot \sin ( \varphi )</math> | |||
==5. Hogyan számítható a hatásos teljesítmény szinuszos feszültség és nem szinuszos áram esetén?== | |||
'''Feladat:''' Hogyan számítja ki a hatásos teljesítményt egy olyan áramkörben, ahol a feszültség görbealakja tisztán szinuszos, de az áramé viszont (az áramkör nemlineritásai miatt) azonos periódusidővel nem szinuszos. | |||
'''Megoldás:''' | |||
Idő szerint kiintegrálom a feszültség és az áram időfüggvényének szorzatát - T a periódusidő: | |||
<math> P = {1 \over T} \int_{0}^{T}\limits u(t) \cdot i(t)\, \mathrm{d} t </math> | |||
Mivel tudjuk, hogy a feszültségnek és az áramerősségnek csak az azonos frekvenciájú komponensei hoznak létre hatásos teljesítményt, így az integrál jóval egyszerűbb alakra is hozható, ahol <math>U_1</math> a szinuszos feszültség effektív értéke, <math>I_1</math> a periodikus áramerősség-függvény első harmonikusában effektív értéke, <math>\varphi_1</math> pedig a feszültség és az áram első harmonikusának fáziskülönbsége: | |||
<math> P = U_1 \cdot I_1 \cdot \cos( \varphi_1 )</math> | |||
==6. Mi a definíciója a villamos energiának (munkának, fogyasztásnak)?== | |||
A villamos energia (munka, fogyasztás) definíció szerint a pillanatnyi teljesítménynek a vizsgált <math>T_1</math> és <math>T_2</math> időpontok között vett idő szerinti integrálja: | |||
<math> W = \int_{T_1}^{T_2}\limits u(t) \cdot i(t)\, \mathrm{d} t </math> | |||
==7. Milyen megvalósítási lehetőségei vannak két villamos mennyiség szorzásának?== | |||
Ez a kérdés körülbelül ugyanaz, mint a következő: | |||
* Hall generátor (a segédáram és a mágneses indukció szorzatával arányos Hall feszültséget szolgáltat) | * Hall generátor (a segédáram és a mágneses indukció szorzatával arányos Hall feszültséget szolgáltat) | ||
* | * Vezérelt áramosztó elvén működő '''analóg szorzó''' (a kimeneti jel arányos a bemeneti jelek szorzatával) | ||
* | * Elektromechanikus szorzó | ||
* | * Kvadratikus szorzó | ||
* időosztásos szorzó | * Időosztásos szorzó | ||
* | * Digitális szorzó | ||
==8. Ismertesse az elektromechanikus, kvadratikus, időosztásos és digitális szorzók elvét!== | |||
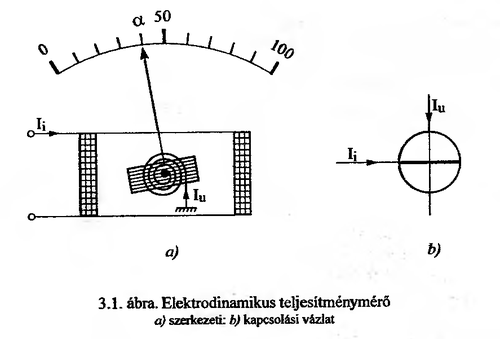
'''Elektromechanikus szorzó:''' | |||
[[File:Labor2_mérés4_ábra1.png|500px]] | |||
A műszer a két jel szorzatával arányos nyomatékot illetve kitérést hoz létre, így a teljesítmény mérésére közvetlenül felhasználható. A műszer állótekercsébe <math>I_i</math> fogyasztói áramot, lengőtekercsébe a fogyasztói feszültséggel arányos <math>I_u</math> áramot kényszerítve a kitérítőnyomaték: | |||
<math> M=k(\alpha)I_i I_u \cos (\varphi)</math> | |||
Ahol <math>k</math> a nemlineáristól, tehát kitéréstől függő skálatényező. | |||
Használható: 0...1000Hz, 0.1% pontossági osztályig! | |||
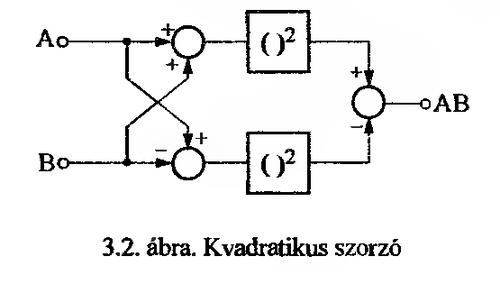
'''Kvadratikus szorzó:''' | |||
[[File:Labor2_mérés4_ábra2.png|500px]] | |||
Az alábbi azonosságra építünk: | |||
<math> (A+B)^2 - (A-B)^2 = A^2 + 2AB +B^2 -A^2 +2AB -B^2 = 4AB</math> | |||
<math> AB = {1 \over 4} \cdot \left( (A+B)^2-(A-B)^2 \right)</math> | |||
Ebből látható, hogy a szorzás visszavezethető összeadásra, kivonásra és négyzetre emelésre, melyek bizonyos korlátokkal már könnyen megvalósíthatóak. | |||
Négyzetre emelés megvalósítása: | |||
*Diódás töréspontos karakterisztikával | |||
*Termoelemmel (1 MHz-ig) | |||
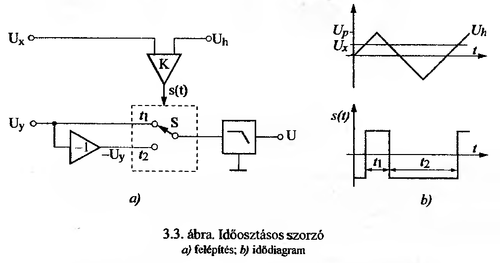
'''Időosztásos szorzó: ''' Jelen példa egyenfeszültségek szorzását valósítja meg! | |||
[[File:Labor2_mérés4_ábra3.png|500px]] | |||
Az <math>U_x</math> bemenőjel és az <math>U_h</math> háromszögjel K komparátorral történő komparalásából előállított <math>s(t)</math> kapcsolójel időviszonyaira az alábbi összefüggés írható fel, ahol <math>U_p</math> a háromszögjel csúcsértéke: | |||
<math>{ U_x \over U_P} = { t_2 - t_1 \over t_2 + t_1}</math> | |||
Az <math>U_y</math> jelet az <math>s(t)</math> kapcsolójellel szorozva és a szorzatból a kapcsolójelet kiszűrve a kapott kimeneti feszültség a két bemenőjel szorzatával arányos lesz: | |||
<math>U= U_y \cdot {t_1 - t_2 \over t_1+t_2} = - {U_x U_y \over U_p}</math> | |||
Határfrekvenciája: 10...100kHz | |||
Pontossága: 0,01% ... 0,1% | |||
'''Digitális szorzó:''' | |||
A jeleket digitalizáljuk és processzorral összeszorozzuk. | |||
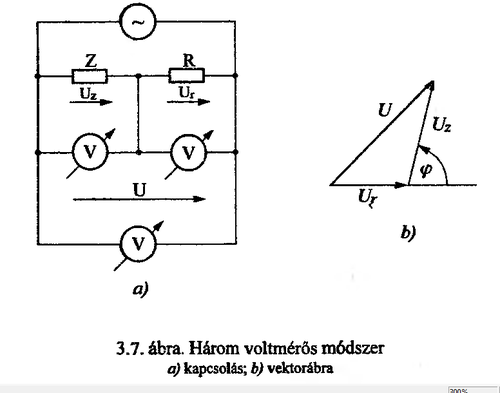
==9. Ismertesse a hatásos teljesítmény mérésének úgynevezett három voltmérős módszerét.== | |||
[[File:Labor2_mérés4_ábra4.png|500px]] | |||
Három voltmérős módszerrel a Z impedancián létrejövő hatásos teljesítmény mérhető. A Z impedanciával sorba kapcsolunk egy R ismert értékű ellenállást és valamennyi részfeszültséget mérve, a vektorábra szerinti háromszögre igazak a következő összefüggések: | |||
<math>U^2 = U_r^2 + U_z^2 + 2U_rU_z\cos ( \varphi) </math> | |||
<math>P= {U_r \over R} U_z \cos ( \varphi)</math> | |||
<math>P = {U^2 - U_r^2 - U_z^2 \over 2R}</math> | |||
==10. Hogyan határozható meg a három voltmérős teljesítménymérés relatív hibája?== | |||
'''Feladat:''' Hogyan határozza meg a hatásos teljesítmény mérésének rendszeres relatív hibáját három voltmérős módszer esetén, ha adott a feszültségmérések relatív rendszeres hibája (a mérést nem terheli véletlen hiba)? | |||
'''Megoldás:''' ''Zoltán István'' méréstechnika könyv 20-21. oldaláról a végeredmény: | |||
Teljes differencia módszerrel: | |||
<math>\Delta P = {1 \over R} \cdot \left( U \cdot \Delta U - U_R \cdot \Delta U_R -U_Z \cdot \Delta U_Z \right)</math> | |||
<math>{ \Delta P \over P} = {2 \over U^2 - U_R^2 - U_Z^2 } \cdot \left( U^2 \cdot {\Delta U \over U} - U_R^2 \cdot {\Delta U_R \over U_R} - U_Z^2 \cdot {\Delta U_Z \over U_Z} \right)</math> | |||
<math>{\Delta U \over U}={\Delta U_R \over U_R}={\Delta U_Z \over U_Z} \longrightarrow { \Delta P \over P} =2 \cdot {\Delta U \over U}</math> | |||
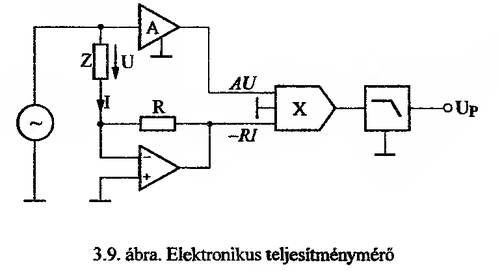
==11. Ismertesse az elektronikus teljesítménymérő elvét!== | |||
[[File:Labor2_mérés4_ábra5.png|500px]] | |||
A fogyasztói árammal illetve a feszültséggel arányos jelek szorzását elektronikus szorzó (rendszerint időosztásos szorzó) végzi. A szorzó kimeneti jelének egyenkomponense a Z impedancián létrejövő hatásos teljesítménnyel arányos. Az egyenkomponenst az aluláteresztő szűrő átengedi. | |||
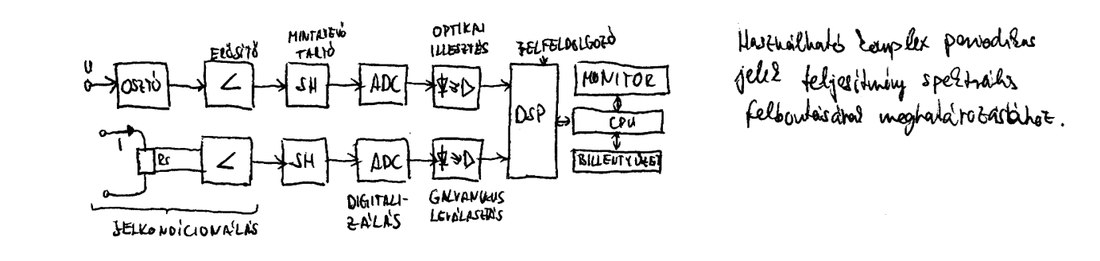
==12. Ismertesse a teljesítmény analizátor elvét!== | |||
[[File:Labor2_mérés4_ábra6.png|1100px]] | |||
A feszültségjel kondicionálását az osztó és az erősítő végzi. Mintavételezés és digitalizálás után az adatok időben sorosan, a csatornák galvanikus függetlenségét biztosító optikai elválasztás közbeiktatásával érkeznek a jelfeldolgozó (DSP) egységbe. Az áramágban egyetlen eltérést az áram mérésére szolgáló Rs sönt jelent. A jelfeldolgozó által szállított részeredményeket a kezelő kérésének megfelelően a központi számítógép (CPU) feldolgozza és az eredményeket a monitoron megjeleníti. | |||
[[ | [[Kategória:Villamosmérnök]] | ||
A lap jelenlegi, 2018. március 8., 09:30-kori változata
1. Hogyan számoljuk ki a pillanatnyi teljesítményt?
A pillanatnyi teljesítmény az áram és feszültség pillanatértékeinek szorzata:
Ha tudjuk, hogy a feszültségünk és az áramunk időfüggvénye is szinuszos, azaz:
Ahol a feszültség és az áram közötti fáziskülönbség, pedig a kezdőfázis.
Felhasználva a hatásos és a meddő teljesítmény képletét:
A pillanatnyi teljesítmény az alábbi alakban is felírható:
2. Megállapodás szerint mit jelent az egyenáramú teljesítmény pozitív vagy negatív előjele?
Ez attól függ, hogy ki kérdezi. Ha egy egyszerű halandó, akkor a pozitív előjel a fogyasztói, negatív a termelői teljesítményt jelenti. Legyen ez most a helyes válasz.
Ha pedig egy VET-es kollega, akkor rá kell kérdezni, hogy milyen irányrendszerben gondolja, mert a fogyasztó irányrendszerben ohmos és induktív jellegű fogyasztó által felvett hatásos és meddő teljesítmény is pozitív (ahogy az előbb), de ugyanígy a tipikus fogyasztót tápláló generátornak is pozitív mind a hatásos, mind pedig a meddő teljesítménye a generátoros pozitív irányrendszerben.
3. Hogyan számítható ki a két-pólus hatásos, meddő és látszólagos teljesítménye?
Feladat: Egy váltakozó áramú áramkörben valamely két-póluson mért feszültség és áram effektív értéke , illetve . a feszültség és az áram közötti fázisszög (a feszültség siet az áramhoz képest, ha pozitív). Hogyan számítható ki a két-pólus hatásos, meddő és látszólagos teljesítménye? Hogyan változnak ezek az értékek, ha a fázisszög előjelet vált?
Megoldás:
Látszólagos teljesítmény
Hatásos teljesítmény
Meddő teljesítmény
Ezek közül csak a meddő teljesítmény előjele változik, ugyanis csak az érzékeny a előjelére, mivel a koszinusz páros függvény.
4. Hogyan definiáljuk a hatásos és meddő teljesítményt, ha periodikus, de nem szinuszos jelekről van szó?
Feladat: Legyen és a feszültség és az áram egyenáramú összetevője, és a feszültség, illetve az áram i-edik felharmonikusának effektív értéke és ezen felharmonikusok közti fázisszög (a feszültség siet az áramhoz képest, ha pozitív).
Megoldás:
Ilyenkor csak az azonos frekvenciájú összetevők hoznak létre teljesítményt!
Hatásos teljesítmény:
Meddő teljesítmény:
5. Hogyan számítható a hatásos teljesítmény szinuszos feszültség és nem szinuszos áram esetén?
Feladat: Hogyan számítja ki a hatásos teljesítményt egy olyan áramkörben, ahol a feszültség görbealakja tisztán szinuszos, de az áramé viszont (az áramkör nemlineritásai miatt) azonos periódusidővel nem szinuszos.
Megoldás:
Idő szerint kiintegrálom a feszültség és az áram időfüggvényének szorzatát - T a periódusidő:
Mivel tudjuk, hogy a feszültségnek és az áramerősségnek csak az azonos frekvenciájú komponensei hoznak létre hatásos teljesítményt, így az integrál jóval egyszerűbb alakra is hozható, ahol a szinuszos feszültség effektív értéke, a periodikus áramerősség-függvény első harmonikusában effektív értéke, pedig a feszültség és az áram első harmonikusának fáziskülönbsége:
6. Mi a definíciója a villamos energiának (munkának, fogyasztásnak)?
A villamos energia (munka, fogyasztás) definíció szerint a pillanatnyi teljesítménynek a vizsgált és időpontok között vett idő szerinti integrálja:
7. Milyen megvalósítási lehetőségei vannak két villamos mennyiség szorzásának?
Ez a kérdés körülbelül ugyanaz, mint a következő:
- Hall generátor (a segédáram és a mágneses indukció szorzatával arányos Hall feszültséget szolgáltat)
- Vezérelt áramosztó elvén működő analóg szorzó (a kimeneti jel arányos a bemeneti jelek szorzatával)
- Elektromechanikus szorzó
- Kvadratikus szorzó
- Időosztásos szorzó
- Digitális szorzó
8. Ismertesse az elektromechanikus, kvadratikus, időosztásos és digitális szorzók elvét!
Elektromechanikus szorzó:
A műszer a két jel szorzatával arányos nyomatékot illetve kitérést hoz létre, így a teljesítmény mérésére közvetlenül felhasználható. A műszer állótekercsébe fogyasztói áramot, lengőtekercsébe a fogyasztói feszültséggel arányos áramot kényszerítve a kitérítőnyomaték:
Ahol a nemlineáristól, tehát kitéréstől függő skálatényező.
Használható: 0...1000Hz, 0.1% pontossági osztályig!
Kvadratikus szorzó:
Az alábbi azonosságra építünk:
Ebből látható, hogy a szorzás visszavezethető összeadásra, kivonásra és négyzetre emelésre, melyek bizonyos korlátokkal már könnyen megvalósíthatóak.
Négyzetre emelés megvalósítása:
- Diódás töréspontos karakterisztikával
- Termoelemmel (1 MHz-ig)
Időosztásos szorzó: Jelen példa egyenfeszültségek szorzását valósítja meg!
Az bemenőjel és az háromszögjel K komparátorral történő komparalásából előállított kapcsolójel időviszonyaira az alábbi összefüggés írható fel, ahol a háromszögjel csúcsértéke:
Az jelet az kapcsolójellel szorozva és a szorzatból a kapcsolójelet kiszűrve a kapott kimeneti feszültség a két bemenőjel szorzatával arányos lesz:
Határfrekvenciája: 10...100kHz
Pontossága: 0,01% ... 0,1%
Digitális szorzó:
A jeleket digitalizáljuk és processzorral összeszorozzuk.
9. Ismertesse a hatásos teljesítmény mérésének úgynevezett három voltmérős módszerét.
Három voltmérős módszerrel a Z impedancián létrejövő hatásos teljesítmény mérhető. A Z impedanciával sorba kapcsolunk egy R ismert értékű ellenállást és valamennyi részfeszültséget mérve, a vektorábra szerinti háromszögre igazak a következő összefüggések:
10. Hogyan határozható meg a három voltmérős teljesítménymérés relatív hibája?
Feladat: Hogyan határozza meg a hatásos teljesítmény mérésének rendszeres relatív hibáját három voltmérős módszer esetén, ha adott a feszültségmérések relatív rendszeres hibája (a mérést nem terheli véletlen hiba)?
Megoldás: Zoltán István méréstechnika könyv 20-21. oldaláról a végeredmény:
Teljes differencia módszerrel:
11. Ismertesse az elektronikus teljesítménymérő elvét!
A fogyasztói árammal illetve a feszültséggel arányos jelek szorzását elektronikus szorzó (rendszerint időosztásos szorzó) végzi. A szorzó kimeneti jelének egyenkomponense a Z impedancián létrejövő hatásos teljesítménnyel arányos. Az egyenkomponenst az aluláteresztő szűrő átengedi.
12. Ismertesse a teljesítmény analizátor elvét!
A feszültségjel kondicionálását az osztó és az erősítő végzi. Mintavételezés és digitalizálás után az adatok időben sorosan, a csatornák galvanikus függetlenségét biztosító optikai elválasztás közbeiktatásával érkeznek a jelfeldolgozó (DSP) egységbe. Az áramágban egyetlen eltérést az áram mérésére szolgáló Rs sönt jelent. A jelfeldolgozó által szállított részeredményeket a kezelő kérésének megfelelően a központi számítógép (CPU) feldolgozza és az eredményeket a monitoron megjeleníti.