„Kódtech ZH 2019” változatai közötti eltérés
A VIK Wikiből
Új oldal, tartalma: „ == 1. feladat == RSA algoritmus p=7, q=17 Kérdés: Melyik a legkisebb használható e? Megoldás: Φ=(p-1)*(q-1)=96, a legkisebb prímszám amivel nem osztható az 5…” |
→a): el volt rontva, n = 6 helyett n= 5 a helyes |
||
| (5 közbenső módosítás, amit 5 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
== 1. | == 1. feladatcsoport (1-3.) == | ||
RSA algoritmus p=7, q=17 | === a) === | ||
Kérdés: | * RSA algoritmus p=7, q=17 | ||
* ''Kérdés'': Adja meg a lehető legkisebb kódoló kulcsként használható exponenst. | |||
* ''Megoldás'': Φ=(p-1)*(q-1)=96, a legkisebb prímszám amivel nem osztható az 5, e=5. | |||
Megoldás: | |||
=== b) === | |||
* ''Kérdés'': Számítsa ki x=11 nyílt szöveghez tartozó y rejtett szövegét. | |||
* ''Megoldás'': y=x^e mod(N)=161051 mod(119)=44 | |||
Megoldás: e | |||
=== c) === | |||
* ''Kérdés'': Határozza meg a dekódoló kulcsot. | |||
* ''Megoldás'': e*d mod(Φ) = 1 | |||
** d=77 (eukledészi algoritmussal szépen, én csak kerestem olyat ahol Φ többszöröse + 1 öttel osztható.) | |||
''' | |||
== 2. feladatcsoport (4.) == | |||
* ''Kérdés'': Jelölje a helyes állításokat az alábbi listán: | |||
12-15. | # A C(15,13) kód Hamming kód-e? Hamis | ||
RS kód QF(7) | # '''A C(8,2) kód szindrómája 6 hosszú. Igaz''' | ||
# Az RSA algoritmusnál a vevő és vételi oldalon ugyanaz a kulcs. Hamis | |||
# '''Az RS kód MDS. Igaz''' | |||
# A C(16,4) kód esetén lehet a dmin 14. Hamis | |||
== 3. feladatcsoport (5-11.) == | |||
[[File:Kódtech_ZH_2019_feladat.PNG | thumb | Feladatkép]] | |||
=== a) === | |||
* ''Kérdés'': Adja meg az n paramétert. | |||
* ''Megoldás'': n = 5 | |||
=== b) === | |||
* ''Kérdés'': Adja meg a k paramétert. | |||
* ''Megoldás'': k = 2 | |||
=== c) === | |||
* ''Kérdés'': Adja meg a dmin-t. | |||
* ''Megoldás'': dmin = 2 | |||
=== d) === | |||
* ''Kérdés'': Hány hibát tud jelezni? | |||
* ''Megoldás'': 1 | |||
=== e) === | |||
* ''Kérdés'': Hány hibát tud javítani? | |||
* ''Megoldás'': 0 | |||
=== f) === | |||
* ''Kérdés'': Adja meg a v vektort. | |||
* ''Megoldás'': v = 00001 | |||
=== g) === | |||
* ''Kérdés'': Adja meg a c’ vektort. | |||
* ''Megoldás'': c’ = 00000 | |||
== 4. feladatcsoport (12-15.) == | |||
* RS kód QF(7) | |||
<math>\underline{\underline{H}}=\begin{bmatrix} | <math>\underline{\underline{H}}=\begin{bmatrix} | ||
| 40. sor: | 68. sor: | ||
1 & 4 & 2 & 1 & 4 & 2\\ | 1 & 4 & 2 & 1 & 4 & 2\\ | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
n= | |||
Megoldás: | === a) === | ||
* ''Kérdés'': Adja meg az n paramétert. | |||
* ''Megoldás'': n = 6 | |||
=== b) === | |||
* ''Kérdés'': Adja meg a k paramétert. | |||
* ''Megoldás'': k = 2 | |||
=== c) === | |||
* ''Kérdés'': Adja meg a dmin-t. | |||
* ''Megoldás'': dmin = 5 | |||
=== d) === | |||
* ''Kérdés'': Hány hibát tud javítani? | |||
* ''Megoldás'': 2 | |||
=== e) === | |||
* ''Kérdés'': Mi a kódszava a csupa kettes üzenetnek? | |||
* ''Megoldás'': c = 416035 | |||
<math>\underline{\underline{G}}=\begin{bmatrix} | |||
1 & 1 & 1 & 1 & 1 & 1\\ | 1 & 1 & 1 & 1 & 1 & 1\\ | ||
1 & 3 & 2 & 6 & 4 & 5\\ | 1 & 3 & 2 & 6 & 4 & 5\\ | ||
\end{bmatrix}</math>, | \end{bmatrix}</math>, | ||
A lap jelenlegi, 2019. december 16., 11:44-kori változata
1. feladatcsoport (1-3.)
a)
- RSA algoritmus p=7, q=17
- Kérdés: Adja meg a lehető legkisebb kódoló kulcsként használható exponenst.
- Megoldás: Φ=(p-1)*(q-1)=96, a legkisebb prímszám amivel nem osztható az 5, e=5.
b)
- Kérdés: Számítsa ki x=11 nyílt szöveghez tartozó y rejtett szövegét.
- Megoldás: y=x^e mod(N)=161051 mod(119)=44
c)
- Kérdés: Határozza meg a dekódoló kulcsot.
- Megoldás: e*d mod(Φ) = 1
- d=77 (eukledészi algoritmussal szépen, én csak kerestem olyat ahol Φ többszöröse + 1 öttel osztható.)
2. feladatcsoport (4.)
- Kérdés: Jelölje a helyes állításokat az alábbi listán:
- A C(15,13) kód Hamming kód-e? Hamis
- A C(8,2) kód szindrómája 6 hosszú. Igaz
- Az RSA algoritmusnál a vevő és vételi oldalon ugyanaz a kulcs. Hamis
- Az RS kód MDS. Igaz
- A C(16,4) kód esetén lehet a dmin 14. Hamis
3. feladatcsoport (5-11.)
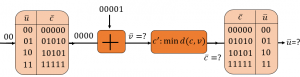
a)
- Kérdés: Adja meg az n paramétert.
- Megoldás: n = 5
b)
- Kérdés: Adja meg a k paramétert.
- Megoldás: k = 2
c)
- Kérdés: Adja meg a dmin-t.
- Megoldás: dmin = 2
d)
- Kérdés: Hány hibát tud jelezni?
- Megoldás: 1
e)
- Kérdés: Hány hibát tud javítani?
- Megoldás: 0
f)
- Kérdés: Adja meg a v vektort.
- Megoldás: v = 00001
g)
- Kérdés: Adja meg a c’ vektort.
- Megoldás: c’ = 00000
4. feladatcsoport (12-15.)
- RS kód QF(7)
a)
- Kérdés: Adja meg az n paramétert.
- Megoldás: n = 6
b)
- Kérdés: Adja meg a k paramétert.
- Megoldás: k = 2
c)
- Kérdés: Adja meg a dmin-t.
- Megoldás: dmin = 5
d)
- Kérdés: Hány hibát tud javítani?
- Megoldás: 2
e)
- Kérdés: Mi a kódszava a csupa kettes üzenetnek?
- Megoldás: c = 416035
,
