„Digit1Beugró” változatai közötti eltérés
a →3. Ellenőrző kérdések: 305 link cserélve, b levéve. |
|||
| (47 közbenső módosítás, amit 15 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
Nem győzöm gyakorlatokon mondani, hogy az itt következő anyagokkal módjával bánjatok. Belenéztem, pár hibás-bizonytalan részt megjelöletem, de nem egy életbiztosítás ebből tanulni, sokatok kisZH-ja ezen bukik el. Nem győzzük azt, hogy egy olyan anyagot nézzünk át/javítsunk folyamatosan, ami közösségi szerkesztésű (meg hát tulajdonképpen van jegyzet :-) ), szóval legyetek óvatosak! Ha valamit nem értesz, inkább kérdezz tőlünk, dolgunk, hogy segítsünk. -- Wacha Gábor, gyakvez | |||
=1. Ellenőrző kérdések= | |||
;101 Mi korlátozza az „analóg elvű” feldolgozó egységekből kialakítható rendszer méreteit? | |||
A p-faktor (megbízhatósági faktor), mely megadja, hogy az alkatrész mekkora valószínűséggel romlik el. Általában: <math>10^{-14} \leq p \leq 10^{-10}</math> | : A csatornába beszűrődő zaj: Távolsági átvitel során a jelhez zaj adódik, amelyet a távolsági közvetítés során használt erősítő felerősít. Analóg egységenként ~0.1% zaj keletkezik. | ||
;102 Mi korlátozza a „digitális elvű” feldolgozó egységekből kialakítható rendszer méreteit? | |||
: A p-faktor (megbízhatósági faktor), mely megadja, hogy az alkatrész mekkora valószínűséggel romlik el. Általában: <math>10^{-14} \leq p \leq 10^{-10}</math> | |||
;103 Milyen feladatai lehetnek a „kódoló egységnek”? | |||
: forráskódolás (tömörítés), csatornakódolás, titkosítás | |||
forráskódolás (tömörítés), csatornakódolás, titkosítás | ;104 Milyen rossz tulajdonságai lehetnek a „csatornának”? | ||
: zaj, támadhatóság, költséges | |||
;105 Mi a „forráskódolás” célja? | |||
: Célja az információ tömörítése (pl. analóg (végtelen) jel digitalizálása (véges adatok)). Egy jelhez egy kódszó rendelése. | |||
;106 Mikor mondjuk egy kódkészletről, hogy megfejthető? | |||
zaj, támadhatóság, költséges | : Egy kód megfejhető, ha a kódszavaiból előállított tetszőleges üzenet egyértelműen felbontható a kód kódszavaira. Ha minden kódszóból visszanyerhető az eredeti információ (pl. prefix kódok (pl. fix hosszuságú kód), végkarakteres kód) | ||
;107 Mi a prefix kód? | |||
: A lehetséges kódszavak közül egyik sem folytatása a másiknak. | |||
;108 Melyik kódolási módszert nevezzük „optimálisnak”? | |||
: Huffman kódolást | |||
Célja az információ tömörítése (pl. analóg (végtelen) jel digitalizálása (véges adatok)). Egy jelhez egy kódszó rendelése. | ;109 Hogyan kell kiszámolni az „átlagos kódhosszt”? | ||
: <math>\bar{l} = \sum p_i l_i</math>, ahol p az előfordulási valószínűség, l a kódszóhossz | |||
;110 Hogyan kell kiszámolni egy forrás „entrópiáját”? | |||
: <math>H(x) = - \sum p_i \log_2(p_i)</math>, ahol p a bekövetkezés valószínűsége | |||
;111 Mi az a „forráskiterjesztés” és mi a célja? | |||
Egy kód megfejhető, ha a kódszavaiból előállított tetszőleges üzenet egyértelműen felbontható a kód kódszavaira. Ha minden kódszóból visszanyerhető az eredeti információ (pl. prefix kódok (pl. fix hosszuságú kód), végkarakteres kód) | : Kettő vagy több esemény egy eseményként kezelése. Célja a kód optimalizálása. | ||
;112 Mennyi a „veszteségmentes tömörítés” alsó határa? | |||
: Az entrópia. | |||
;113 Mennyi a „veszteséges tömörítés” alsó határa? | |||
: Nincs alsó határa, maximum elveszítjük az összes adatot. | |||
A lehetséges kódszavak közül egyik sem folytatása a másiknak. | ;114 Mi a „folt hiba” és mi a „véletlen hiba”? | ||
: Folt hiba: átvitel során több egymás utáni hiba. Véletlen hiba: átvitel során véletlenül, nem egymás után bekövetkezett hibák. | |||
;115 Mi az „eltörlődéses hiba”? | |||
: Az átvitel során egy bit törlődik, de a hibát észreveszi a vevő. | |||
;116 Mi az „átállítódásos hiba”? | |||
Huffman kódolást | : Az átvitel során egy bit értéke invertálódik. | ||
;117 Milyen hibavédelmi stratégiákat ismer? | |||
: paritásbit | |||
: ismétléses kód | |||
: Hamming-kód (többszörös paritásbit a kódszó bitcsoportjaira) | |||
<math>\bar{l} = \sum p_i l_i</math>, ahol p az előfordulási valószínűség, l a kódszóhossz | : többszörös elküldés | ||
;118 Egy <math>d_{min}</math> Hamming távolságú kód mire használható eltörlődéses csatornánál? | |||
: Hibajelzésre n hosszig, hibajavításra <math>d_{min} - 1</math> hosszig. | |||
;119 Egy <math>d_{min}</math> Hamming távolságú kód mire használható átállítódásos csatornánál? | |||
: Hibajelzésre <math>d_{min}-1</math> hosszig, hibajavításra <math>\frac{d_{min}-1}{2}</math> alsó egészrészéig | |||
<math>H(x) = - \sum p_i \ | ;120 q elemű abc-ből képzett k hosszúságú információt akarunk védeni paritáskóddal. Milyen hosszú lesz a kód, mekkora lesz a Hamming távolsága és hogyan kell megkonstruálni a redundáns részt? | ||
: k+1 hosszúságú lesz a kód. Az ABC minden eleméhez hozzárendelünk egy számot. Előre eldöntjük, hogy az összegük páratlan vagy páros lesz a teljes kódszóban és az alapján teszünk a kódszó végére redundáns részt. A Hamming-távolság 2. | |||
;121 Mennyi a Hamming kód Hamming távolsága és milyen hibavédelemre használható? | |||
: H=3, Egy hiba javítására alkalmas, vagy két hiba jelzésére. | |||
;122 Milyen számábrázolási módszereket tanultunk? | |||
Kettő vagy több esemény egy eseményként kezelése. Célja a kód optimalizálása. | : előjeles abszolútértékes | ||
: egyes komplemens | |||
: kettes komplemens | |||
: offszet | |||
;123 Írja fel 5 biten a decimális +9 és -9 értékeit a tanult számábrázolásokban! | |||
Az entrópia. | |||
Nincs alsó határa, maximum | |||
Folt hiba: átvitel során több egymás utáni hiba. Véletlen hiba: átvitel során véletlenül, nem egymás után bekövetkezett hibák. | |||
Az átvitel során egy bit törlődik, de a hibát észreveszi a vevő. | |||
Az átvitel során egy bit értéke invertálódik. | |||
Hibajelzésre n hosszig, hibajavításra <math>d_{min} - 1</math> hosszig. | |||
Hibajelzésre <math>d_{min}-1</math> hosszig, hibajavításra <math>\frac{d_{min}-1}{2}</math> alsó egészrészéig | |||
k+1 hosszúságú lesz a kód. Az ABC minden eleméhez hozzárendelünk egy számot. Előre eldöntjük, hogy az összegük páratlan vagy páros lesz a teljes kódszóban és az alapján teszünk a kódszó végére redundáns részt. A Hamming-távolság 2. | |||
használható? | |||
H=3, Egy hiba javítására alkalmas, vagy két hiba jelzésére. | |||
{| border="1" style="text-align:center" | {| border="1" style="text-align:center" | ||
| Számábrázolás || +9 || -9 | | Számábrázolás || +9 || -9 | ||
| 130. sor: | 66. sor: | ||
| Offszet || 11001 || 00111 | | Offszet || 11001 || 00111 | ||
|} | |} | ||
;124 Milyen tulajdonságú kódokat nevezünk „pozíciókódnak”? | |||
: Az egymásután következő pozíciók kódjának Hamming-távolsága egy. | |||
;125 Milyen pozíciókódokat ismer és n biten hány pozíció kódolható velük? | |||
: Gray-kód: n biten <math>2^n</math> pozíció. Generálása rekurzív módon, tükrözéses módszerrel történik. | |||
Az egymásután következő pozíciók kódjának Hamming-távolsága egy. | : Johnson-kód: n biten 2n pozíció | ||
Gray-kód: n biten <math>2^n</math> pozíció. Generálása rekurzív módon, tükrözéses módszerrel történik. | |||
Johnson-kód: n biten 2n pozíció | |||
=2. Ellenőrző kérdések= | =2. Ellenőrző kérdések= | ||
;201 Írja fel a Boole algebra kommutativitási axiómáit | |||
: <math>A*B=B*A</math> | |||
: <math>A+B=B+A</math> | |||
;202 Írja fel a Boole algebra disztributivitási axiómáit! | |||
: <math>A*(B+C)=AB+AC</math> | |||
: <math>A+(B*C)=(A+B)*(A+C)</math> | |||
;203 Mi a Boole algebrában a dualitás elve? | |||
: A 0-ák és 1-ek valamint a VAGY és ÉS műveletek felcserélhetőek. | |||
;204 Írja fel a DeMorgan azonosságot! | |||
: <math>\overline{A*B} = \bar{A} + \bar{B}</math> | |||
: <math>\overline{A+B} = \bar{A}*\bar{B}</math> | |||
;205 Írja fel a Boole algebra negálás műveletét meghatározó definíciót! | |||
: Minden <math>A</math> esetén létezik olyan <math>\bar{A}</math>, hogy: | |||
: <math>A+\bar{A}=1</math> | |||
: <math>A*\bar{A}=0</math> | |||
;206. Elnyelési tulajdonság | |||
: <math>A*(A+B)=A</math>, illetve a dualitás elve miatt <math>A+(B*A)=A</math> | |||
;207. Írja fel a Boole algebrában a konstanssal való műveletek eredményeit (A.0, A.1,A+0, A+1)! | |||
: <math>A*0=0</math> | |||
: <math>A*1=A</math> | |||
: <math>A+0=A</math> | |||
: <math>A+1=1</math> | |||
;208 Hány különböző n változós logikai függvény van <math>Z=(a_1,a_2,a_3,...,a_n)</math>? | |||
: <math>2^{2^n}</math> | |||
;209 Mi az a diszjunktív algebrai normál alak? | |||
: Szorzatok összege (ÉSek VAGYa) | |||
;210 Mi az a konjunktív algebrai normál alak? | |||
: Összegek szorzata (VAGYok ÉSe) | |||
;211 Melyek a kétváltozós szimmetrikus logikai függvények (amelyek nem változnak, ha a két változót felcseréljük) | |||
: ÉS, VAGY, XOR, NAND (not and), NOR (not or), ekvivalencia (not xor) | |||
;212 Rajzolja fel és peremezze az ABCD változókra a a Karnaugh táblát és jelölje be az <math>\bar{A}*B*\bar{C}*D</math> minterm helyét! | |||
: [[File:Digit1_beugro_212.jpg]] | |||
;213 Rajzolja fel az <math>A+B*\bar{C}</math> függvényt Karnaugh táblán! | |||
: [[File:Digit1_beugro_213.jpg]] | |||
;214 Rajzolja fel az <math>A+B*\bar{C}</math> függvényt igazságtáblában. | |||
{| style="text-align:center" | |||
|A||B||C||<math>A+B*\bar{C}</math> | |||
|- | |||
|0||0||0||0 | |||
|- | |||
|0||0||1||0 | |||
|- | |||
|0||1||0||1 | |||
|- | |||
|0||1||1||0 | |||
|- | |||
|1||0||0||1 | |||
|- | |||
|1||0||1||1 | |||
|- | |||
|1||1||0||1 | |||
|- | |||
|1||1||1||1 | |||
|} | |||
;215 Mi az a minterm és mi az a maxterm? | |||
: Diszjunktív normál alaknál az egyes tagok az igazságtábla 1-eseit valósítják meg, ezek a mintermek. | |||
: Konjunktív normál alaknál az egyes tagok az igazságtábla 0-áit valósítják meg, ezek a maxtermek. | |||
;216 Kombinációs hálózatok milyen leírási formáit ismeri? | |||
: Szöveges, algebrai kifejezés, igazság-táblázat, kapcsolási rajz (szimbólumokkal) | |||
;217 A Boole algebra alapműveleteinek mik a megfelelői a halmazalgebrában? | |||
: ÉS = metszet | |||
: VAGY = unió | |||
: NEM = komplementer/negát | |||
;218 A Boole algebra alapműveleteinek mik a megfelelői a kapcsoló algebrában? | |||
: ÉS = soros | |||
: VAGY = párhuzamos | |||
: NEM = fordított kapcsoló | |||
;219 Milyen elnevezéseit ismeri még a mod2 (<math>\oplus</math>) műveletnek? | |||
: kizáró VAGY (exclusive OR, EXOR, XOR) | |||
: antivalencia | |||
;220 Melyek azok a kétváltozós műveletek, amelyek Karnaugh táblájában két darab 1-es van? | |||
: XOR /antivalencia/ | |||
: XNOR /ekvivalencia/ | |||
;221 Melyek azok a kétváltozós műveletek, amelyek Karnaugh táblájában egy darab 1-es van? | |||
: AND | |||
: NOR | |||
;222 Rajzolja fel az AND, OR, NAND, NOR kapuk kapcsolási szimbólumait egy választott szabvány szerint! Melyik szabványt választotta? | |||
: [[File:Digit1_beugro_222.jpg]] | |||
;223 Mire jó az előadáson tanult teljes összeadó? Írja fel logikai függvényeit! | |||
: Két darab 1 bites szám összeadására alkalmas. | |||
: <math>S_i=A_i \oplus B_i \oplus C_{i-1}</math> | |||
: <math>C_i=A_i*B_i+A_i*C_{i-1}+B_i*C_{i-1}</math> | |||
<math>A+B=B+A | =3. Ellenőrző kérdések= | ||
;301 Mi a don't care kombináció? | |||
: Valamely minterm esetén lényegtelen az eredmény. | |||
;302 Miért lehet egy kombinációs hálózat specifikációjában don't care minterm? | |||
: vagy azért mert a bemeneten soha nem történik meg. | |||
: vagy azért mert ha igen, akkor nincs hatása a kimeneten. | |||
;303 Rajzoljon fel egy vízszintes elrendezésű öt változós K táblát és peremezze az ABCDE változókkal a szokásos sorrendben! | |||
: [[File:Digit1_beugro_303.jpg]] | |||
;304 Jelölje be egy K táblába az <math>A\bar{B}\bar{C}</math> mintermet! | |||
: [[File:Digit1_beugro_304.jpg]] | |||
;305 Jelölje be egy K táblába az (A+/B+/C) maxtermet! | |||
: [[File:Digit1_beugro_305.jpg]] | |||
;306 Jelölje be egy K táblába az A./C primimplikánst! | |||
: [[File:Digit1_beugro_306.jpg]] | |||
;307 Jelölje be egy K táblába az (A+/C) primimplikánst! | |||
: [[File:Digit1_beugro_307b.jpg]] | |||
;308 Rajzolja be egy K táblába az F = A.B + /A.C függvényt! | |||
: [[File:Digit1_beugro_308.jpg]] | |||
;309 Rajzolja be egy K táblába az F = [(A mod2 B) + A./C] függvényt! | |||
: [[File:Digit1_beugro_309.jpg]] | |||
;310 Rajzolja be egy K táblába az F = A.B + A./C + B./C függvényt! | |||
: [[File:Digit1_beugro_310.jpg]] | |||
;311 Mi az a lényeges prímimplikáns? | |||
: Olyan term, amelyből nem hagyható el több változó vagyis nem egyszerűsíthető tovább. Azon prímimplikánsokat, melyek legalább egy megkülönböztetett mintermet tartalmaznak, lényeges prímimplikánsoknak hívjuk. | |||
;312 Mire jó a lefedési tábla? | |||
: Megtudhatjuk a segítségével, hogy melyik pirimimplikánsokat hagyhatjuk el a függvény megvalósításához, ezzel olcsóbbá téve a kapcsolást. | |||
;313 Mi a több kimenetű logikai függvények minimalizálásának alapelve? | |||
: A több függvényben is előforduló (azonos) prímimplikánsokat csak egyszer valósítjuk meg. | |||
;314 Mik a tanult minimalizálási módszer korlátjai? | |||
: Csak 2 szintű diszjunktív vagy konjunktív alakban megadott hálózatokat lehet vele minimalizálni | |||
;315 Mire optimalizál a tanult minimalizálási módszer? | |||
: a bemenetek számára | |||
;316 Milyen a több szintű ÉS-VAGY típusú hálózat? | |||
: A többszintü ÉS-VAGY hálozatokban csak ÉS és VAGY kapu található, szintenként egyfajta, egymást váltva. | |||
A következőkhöz azért lenne hozzáfűzésem: | |||
Felmerül bennem a kérdés, hogy a NOT az NAND (vagy NOR) kapu-e... Elfogadtam kisZH-ban, de jobban örültem, amikor valaki a NOT-ot is NAND-dal vagy NOR-ral valósította meg (Wacha Gábor) | |||
--[[Szerkesztő:Halftome|Halftome]] ([[Szerkesztővita:Halftome|vita]]) 2013. november 5., 19:38 (UTC) A "NOT", az egy inverter. Ha NAND vagy NOR kapunak a bemeneti lábait összekötjük, egy egyszerű invertert kapunk. | |||
A 0- | ;317 Valósítsa meg az F = A.B függvényt csak NAND kapuval! | ||
: NOT (A NAND B) | |||
;318 Valósítsa meg az F = A+B függvényt csak NAND kapuval! | |||
: NOT A NAND NOT B | |||
;319 Valósítsa meg az F = A.B függvényt csak NOR kapuval! | |||
: NOT A NOR NOT B | |||
;320 Valósítsa meg az F = A+B függvényt csak NOR kapuval! | |||
: NOT (A NOR B) | |||
;321 Milyen hazárd-típusokat tanultunk? | |||
: dinamikus, statikus , funkcionális | |||
;322 Mi az a statikus hazárd? | |||
: A kimenet a változás után ugyanolyan értékű lenne, mint előtte, de a késleltetéstől függően rövid ideig a kimenet átvált (0-ról 1-re vagy 1-ről 0-ra) (“szőrös lesz”) majd beáll a kívánt állapot. | |||
(Ezt a "szőrős lesz"-t kérlek, ne írjátok -- Wacha Gábor) | |||
;323 Mi a az a dinamikus hazárd? | |||
: A kimenet szomszédos BEMENETI változás után át váltana (0->1 vagy 1->0), de a késleltetéstől függően rövid ideig ide-oda váltogat, majd beáll a kívánt állapot. | |||
;324 Mi az a funkcionális hazárd? | |||
: Egyszerre több bemenet változik meg (jellegre lehet olyan mint a statikus vagy a dinamikus hazárd) | |||
;325 ÉS-VAGY típusú hálózatokban mi a statikus hazárd feltétele? | |||
: legalább két szintű hálózat + egy változó több úton juthat kimenetre | |||
;326 ÉS-VAGY típusú hálózatokban mi a dinamikus hazárd feltétele? | |||
: legalább három szintű hálózat és statikus hazárd alacsonyabb szinten | |||
;327 ÉS-VAGY típusú hálózatokban mi a hazárd kiküszöbölésének módja? | |||
: Hazárdmentesítő primimplikánsok használata | |||
: És ez mit jelent? Egészítsétek már ki... (Wacha Gábor) | |||
: Olyan prímimplikánsokat realizálunk szomszédos hurkok között, melyek nincsenek átfogó lefedéssel kezelve vagy jelút érzékenyítés alapján. | |||
=4. Ellenőrző kérdések= | |||
;401 Rajzoljon olyan kapcsolást, amelyik egy jel felfutó éléből impulzust csinál! | |||
: [[File:Digit1_beugro_401.jpg ]] | |||
;402 Rajzoljon olyan kapcsolást, amelyik egy jel lefutó éléből impulzust csinál! | |||
: [[File:Digit1_beugro_20131027_403.png ]] | |||
;403 Rajzoljon olyan kapcsolást, amely egy jel fel- és lefutó éléből is impulzust csinál! | |||
: [[File:Digit1_beugro_20131027_402.png ]] | |||
;404 Mit nevezünk egy függvényrendszer lezártjának? | |||
: A függvényrendszer függvényeinek ismételt alkalmazásával előállítható függvények halmazát (függvények változóiba behelyettesítünk függvényeket) | |||
;405 Mi az a "funkcionálisan teljes" függvényrendszer? | |||
: F függvényhalmazra funkcionálisan teljes fv.rendszer f, ha f lezártja F ([f] = F). (a lezárás inverz művelete, a függvények bázisait adja) | |||
;406 Írjon két példát az "összes Boole függvény" funkcionálisan teljes függvényrendszerére! | |||
: + , NOT | |||
: . , NOT | |||
: + , NOT | |||
: NAND | |||
: NOR | |||
: XOR , 1 | |||
;407 Mi ütemezi a szinkron sorrendi hálózat állapotváltozásait? | |||
: Az órajel | |||
;408 Mi ütemezi az aszinkron sorrendi hálózat állapotváltozásait? | |||
: Visszacsatoló ágalban Y periodikusan nyitjuk zárjuk a kapcsolókat | |||
;409 Írja fel a Mealy-modell működését leíró egyenleteket! | |||
: <math>Y^t = f(Q^t, x^t)</math> | |||
: <math>Q^{t+1} = f(Q^t, x^t)</math> | |||
;410 Írja fel a Moore-modell működését leíró egyenleteket! | |||
: <math>Y^t = f(Q^t)</math> | |||
: <math>Q^{t+1} = f(Q^t)</math> | |||
;411 Jellemezze szavakban a Mealy-modellt! | |||
A kimenet az aktuális állapot és az aktuális bemenet függvénye. | |||
;412 Jellemezze szavakban a Moore-modellt! | |||
: A kimenet csak az aktuális állapottól függ. | |||
;413 Rajzolja fel a Mealy-modell blokkvázlatát! | |||
: [[File:Digit1_beugro_413.jpg]] | |||
;414 Rajzolja fel a Moore-modell blokkvázlatát! | |||
: [[File:Digit1_beugro_414.jpg]] | |||
;415 Mi jellemzi a szinkron sorrendi hálózatot? | |||
: A szinkron sorrendi hálózat állapotait memória tulajdonságú alkatrészek (flip-flopok) tárolják, egy órajellel ütemezett időpontokban. | |||
;416 Rajzolja fel egy D FF állapotgráfját! | |||
: [[File:Digit1_beugro_416.jpg]] | |||
;417 Rajzolja fel egy T FF állapotgráfját! | |||
: [[File:Digit1_beugro_417.jpg]] | |||
;418 Rajzolja fel egy JK FF állapotgráfját! | |||
: [[File:Digit1_beugro_418.jpg]] | |||
;419 Írja fel egy D FF vezérlési egyenletét! | |||
: <math>Q^{t+1}=D^t</math> | |||
;420 Írja fel egy T FF vezérlési egyenletét! | |||
: <math>Q^{t+1}=T^t mod_2 {Q^t}</math> | |||
;421 Írja fel egy JK FF vezérlési egyenletét! | |||
: <math>Q^{t+1}=Q^t*\bar{K^t}+\bar{Q^t}*J^t</math> | |||
;422 Rajzolja fel egy D FF állapotátmeneti tábláját! | |||
{| style="text-align:center;text-align:center;border:solid 1px" border="1" | | |||
!<math>D^t</math>!!<math>Q^t</math>!!<math>Q^{t+1}</math> | |||
|- | |||
|0||0||0 | |||
|- | |||
|0||1||0 | |||
|- | |||
|1||0||1 | |||
|- | |||
|1||1||1 | |||
|} | |||
;423 Rajzolja fel egy T FF állapotátmeneti tábláját! | |||
{| style="text-align:center;text-align:center;border:solid 1px" border="1" | | |||
!<math>T^t</math>!!<math>Q^t</math>!!<math>Q^{T+1}</math> | |||
|- | |||
|0||0||0 | |||
|- | |||
|0||1||1 | |||
|- | |||
|1||0||1 | |||
|- | |||
|1||1||0 | |||
|} | |||
;424 Rajzolja fel egy JK FF állapotátmeneti tábláját! | |||
{| style="text-align:center;text-align:center;border:solid 1px" border="1" | | |||
!<math>J^t</math>!!<math>K^t</math>!!<math>Q^t</math>!!<math>Q^{t+1}</math> | |||
|- | |||
|0||0||0||0 | |||
|- | |||
|0||0||1||1 | |||
|- | |||
|0||1||0||0 | |||
|- | |||
|0||1||1||0 | |||
|- | |||
|1||0||0||1 | |||
|- | |||
|1||0||1||1 | |||
|- | |||
|1||1||0||1 | |||
|- | |||
|1||1||1||0 | |||
|} | |||
VAGY | |||
{| style="text-align:center;border: solid 1px" border="1" | |||
| rowspan="2" |Qt|| colspan="2" |J=0|| colspan="2"|J=1 | |||
|- | |||
| K=0 || K=1 || K=0 || K=1 | |||
|- | |||
|a||a/0||a/0||b/1||b/1 | |||
|- | |||
|b||b/1||a/0||b/1||a/0 | |||
|} | |||
;425 Csináljon JK FF-ból T FF-ot! | |||
: [[File:Digit1_beugro_425.jpg]] | |||
;426 Csináljon JK FF-ból D FF-ot! | |||
: [[File:Digit1_beugro_426.jpg]] | |||
;427 Mit csinál az RS FF a különböző vezérlések mellett? | |||
: 00 - marad | |||
: 01 - 1-be állít | |||
: 10 - 0-ba állít | |||
: 11 - TILOS | |||
;428 Mit csinál a JK FF a különböző vezérlések mellett? | |||
: 00 - marad | |||
: 01 - 0-ba állít | |||
: 10 - 1-be állít | |||
: 11 - invertál | |||
;429 Rajzoljon fel egy 3 bites szinkron bináris felfelé számlálót! | |||
: [[File:Digit1_beugro_429.jpg]] | |||
;430 Rajzoljon fel egy 3 bites shiftregisztert! | |||
: [[File:Digit1_beugro_430.jpg]] | |||
=5. Ellenőrző kérdések= | |||
;Megjegyezném, hogy ezekben is találtam hibákat, javítsátok. (Azért ti, hogy tanuljatok belőle, ez ilyen oktatói hülyeség). WachaG | |||
;501 Mik jellemzik a TSH hálózatokat? | |||
: Egy automata teljesen specifikált (TSH), ha az összes következő állapota (Qt+1) és kimenete (Y) specifikált. | |||
;502 Mik jellemzik az NTSH hálózatokat? | |||
: Van az állapottáblában olyan kimenet vagy következő állapot, ami nem specifikált (tartalmaz don't care-t) | |||
;503 Milyen állapotminimalizálási módszereket ismer? | |||
: Partíciófinomítás, lépcsős-táblás módszer | |||
;504 Mi adja a partíciófinomítás első partícióját? | |||
: Megadott bemenetekre eltérő kimenetet adó esetek 1-1 külön csoportot alkotnak. | |||
;505 Mikor zárt egy particionálás? | |||
: Egy adott partíción belüli állapotokból, adott bemenetre azonos partícióba megyünk. | |||
;506 Írja fel az állapotekvivalencia rekurzív definícióját! | |||
: <math>q_i \equiv q_j</math>, ha bármely lehetséges bemenetre érvényes, hogy a kimenet azonos | |||
: <math>g(q_i,x_k) = g(q_i,x_k)</math> | |||
Ez megint pontatlan így. (wachag) | |||
Egyfelől, mi az a g? Írjátok már oda a kisZH-ba, mert akármivel jelölhetsz akármit... | |||
Másfelől meg mit jelent a képlet? Meg mik ezek az indexek? Amik ráadásul hibásak... | |||
;507 Írja fel az állapotkompatibilitás rekurzív definicióját! | |||
: <math>q_i \sim q_j</math>, ha bármely érvényes bemenetre a specifikált helyeken, hogy <math>g(q_i,x_k) = g(q_i,x_k)</math> és <math>f(q_i,x_k) \sim f(q_i,x_k)</math> | |||
Megint: mi az a g és mi az az f? Miért ne írhatná valaki ezt: | |||
: <math>q_i \sim q_j</math>, ha bármely érvényes bemenetre a specifikált helyeken, hogy <math>triceratops(q_i,x_k) = triceratops(q_i,x_k)</math> és <math>velociraptor(q_i,x_k) \sim velociraptor(q_i,x_k)</math> | |||
Ennek is van értelme, de ugyanúgy nem derül ki belőle semmi. (wachag) | |||
Arról már nem is beszélve, hogy az indexek megint nem stimmelnek... | |||
;508 Mi jellemzi a maximális ekvivalencia osztályozást? | |||
: Az egyes osztályok nem bővíthetőek új állapottal. Minden állapot benne van 1 osztályban, és ezek páronként ekvivalensek. | |||
;509 Mi jellemzi a maximális kompatibilitási osztályozást? | |||
: Nincs több olyan állapot, ami az osztály összes tagjával kompatibilis lenne. 1 osztály állapotai páronként kompatibilisek, és maximális nagyságúak. | |||
;510 Egy állapot hány helyen lehet a max. kompatibilitási osztályozásban? | |||
: Annyi helyen lehet, ahány olyan osztály van, melynek minden tagjával kompatibilis. Ez akár az összes kompatibilitási osztály is lehet. | |||
;511 Milyen hálózatokhoz javasoljuk a partíciófinomítást? | |||
: TSH | |||
;512 Milyen hálózatokhoz javasoljuk a lépcsős táblás módszert? | |||
: TSH, NTSH | |||
;513 Fogalmazza meg a szomszédos kódolás feltételét a "soronkövetkező állapotok" alapján! | |||
: Ha van olyan lehetséges bemenet (<math>x_k</math>), hogy a két állapot (<math>q_i, q_j</math>) soronkövetkező állapota azonos, akkor az ezek közti Hamming-távolság (<math>d_{min}</math>) legyen 1. | |||
: Legyen <math>d_{min} = 1</math>, ha <math>q_i,q_j</math>-re <math>f(q_i, x_k) = f(q_j, x_k)</math>. | |||
;514 Fogalmazza meg a szomszédos kódolás feltételét a "megelőző állapotok" alapján! | |||
: Ha <math>q_i,q_j</math> soronkövetkező állapota <math>q_m</math>-nek, akkor Hamming-távolságuk legyen 1. | |||
: Legyen <math>d_min = 1</math>, ha <math>q_i,q_j</math>-re <math>q_i=f(q_m, x_k)</math> és <math>q_j=f(q_m, x_l)</math>. | |||
;515 n biten M állapotnak hányféle "különböző költségű" állapotkódolása van? | |||
: <math>\frac{ (^{2^n} _M )M! }{2^n n!}</math> | |||
;516 Milyen átalakításokkal biztosan nem változik egy állapotkódolás költsége? | |||
: A kódbitek átnevezésével vagy invertálásával. | |||
;517 Mit jelent az, hogy "előírt kimenet alapján" kódolunk? | |||
: Adott bemeneti kombinációra azonos kimenetet adó állapotok kódját úgy választjuk meg, hogy egy bitben térjenek el(Hamming-távolságuk 1 legyen). | |||
;518 Miket nevezünk önfüggő szekunder változóknak? | |||
: Olyan állapotcsoportot, amiben a következő értékek csak a csoporton belüli változóktól függ, a csoporton kívüli állapotoktól nem. Például: | |||
: Két állapot: <math>Q_a, Q_b</math> | |||
: És <math>Q_a^{t+1} = f(Q_a^t, X^t)</math>, | |||
: <math>Q_b^{t+1} = f'(Q_a^t, Q_b^t, X^t)</math> | |||
: Ekkor <math>Q_a</math> egy önfüggő szekunder változócsoportot alkot, mert más változótól nem függ. <math>Q_b</math>-re ez nem igaz, mert függ <math>Q_a</math>-tól. | |||
: <math>Q_a, Q_b</math> együtt önfüggő szekunder változócsoportot alkot, hisz nem függnek a csoporton kívüli változótól (itt nincs is több változó, ez triviális). | |||
;519 Milyen triviális HT particiókat ismer? | |||
: Ha minden állapot 1 db osztályban van, és ha minden állapot külön-külön osztályban van. | |||
Ez így szerencsétlen megfogalmazás. "vagy ha minden". wachag | |||
;520 Mi jellemzi a HT particionálás osztályait? | |||
: Helyettesítési tulajdonságú partíció. az osztályok zártak, ha kimenet nem vesszük figyelembe. Egy osztály minden állapotából, adott bemenet hatására, egy adott osztály valamelyik állapotába jutunk. | |||
;521 Mikor zárt egy HT particionálás? | |||
: Ha egy osztály minden átmenete azonos osztályba megy át. | |||
;522 Mikor alakul ki a hálózat párhuzamos dekompoziciója? | |||
: Két ortogonális HT partíció alapján kódolva, párhuzamos dekompozíció alakul ki. | |||
;523 Mikor alakul ki a hálózat soros dekompoziciója? | |||
: Egy HT partíció alapján kódolva soros dekompozíció alakul ki. | |||
;524 Mikor ortogonális két HT particionálás? | |||
: Amikor partíciók blokkjainak metszete maximum 1 állapotot tartalmaz és az összes állapot szerepel benne, vagyis ortogonálisak. | |||
;525 Milyen HT particiót talál "ciklikus" feladatokban? | |||
: Ortogonálist. | |||
=6. Ellenőrző kérdések= | |||
;601 Milyen okai vannak az órajelcsúszásnak? | |||
: Eltérő futási idők, eltérő komparálási szint, eltérő meghajtó. | |||
;602 Milyen hibákat okozhat az órajelcsúszás? | |||
: Ha az órajelcsúszás nagyobb mint a biztonsági idő, akkor a flipflopok különböző állapotok alapján vesznek mintát, és nem megfelelő állapotba váltanak. | |||
;603 Hogyan küszöbölhető ki az órajelcsúszás okozta hiba? | |||
: A Master-Slave elvvel, azaz a biztonsági idő meghosszabbításával. | |||
;604 Master-Slave FF-nál melyik fokozat adja kimenetet? | |||
: A slave | |||
;605 Rajzoljon fel D FF-okból egy kettős élvezérelt MS FF-ot! | |||
: [[File:Digit1_beugro_605.jpg]] | |||
;606 Rajzoljon fel egy kettős élvezérelt JK MS-FF-ot! | |||
: [[File:Digit1_beugro_606.jpg]] | |||
;607 Mi ütemezi az aszinkron sorrendi hálózat állapotváltozását? | |||
: A bemenet változása. | |||
;608 Miben különbözik az aszinkron sorrendi hálózat a szinkrontól? | |||
: A szinkron hálózatokban minden órajel vezérelt, míg az aszinkronban a bemeneti jelek megváltozásától függ a rendszer állapota | |||
;609 Mik az FMA feltételek (alapvető működésű aszinkron hálózat feltételei)? | |||
: 1. egyszerre 1 időpillanatban csak 1 bemenet változik (a bemeneten csak 1 Hamming-távú változás) | |||
: 2. újabb változás csak akkor lehetséges, ha az előző bemenetváltásból következő átmeneti állapot már lezajlott (csak stabil állapotban történik bemeneti változás) | |||
;610 Rajzolja fel egy aszinkron /R/S FF kapcsolását! | |||
: [[File:Digit1_beugro_610.jpg]] | |||
;611 Rajzolja fel egy aszinkron RS FF kapcsolását! | |||
: [[File:Digit1_beugro_611.jpg]] | |||
;612 Hogyan kell vezérelni az aszinkron /R/S FF-ot ahhoz, hogy a különböző állapotátmeneteket megvalósíthassuk? | |||
{| | |||
| <math>Y^t</math> || <math>Y^{t+1}</math> || <math>\bar{R}</math> || <math>\bar{S}</math> | |||
|- | |||
| 0 || 0 || - || 1 | |||
|- | |||
|0 || 1 || 1 || 0 | |||
|- | |||
|1 || 0 || 0 || 1 | |||
|- | |||
|1 || 1 || 1 || - | |||
|- | |||
|} | |||
;613 Hogyan kell vezérelni az aszinkron RS FF-ot ahhoz, hogy a különböző állapotátmeneteket megvalósíthassuk? | |||
{| | |||
| <math>Y^t</math> || <math>Y^{t+1}</math> || R || S | |||
|- | |||
| 0 || 0 || - || 0 | |||
|- | |||
|0 || 1 || 0 || 1 | |||
|- | |||
|1 || 0 || 1 || 0 | |||
|- | |||
|1 || 1 || 0 || - | |||
|- | |||
|} | |||
;614 Hogyan működik az aszinkron DG FF? | |||
: Ha G=0, akkor az FF nincs engedélyezve, és a régi állapotra emlékszik. | |||
: Ha G=1, akkor az FF engedélyezve van, és a D-n levő értéket beírja magába, mint új állapot. | |||
;615 Hogyan kell vezérelni az aszinkron DG FF-ot ahhoz, hogy a különböző állapotátmeneteket megvalósíthassuk? | |||
{| | |||
| <math>Y^t</math> || <math>Y^{t+1}</math> || D || G | |||
|- | |||
|rowspan="2"| 0 || rowspan="2" | 0 || - || 0 | |||
|- | |||
| 0 || 1 | |||
|- | |||
|0 || 1 || 1 || 1 | |||
|- | |||
|1 || 0 || 0 || 1 | |||
|- | |||
|rowspan="2"| 1 || rowspan="2"| 1 || - || 0 | |||
|- | |||
| 1 || 1 | |||
|} | |||
;616 Mi jellemzi az előzetes (primitív) állapottáblát? | |||
: Minden sorban csak 1 stabil állapot van. | |||
;617 Mi az a versenyhelyzet? | |||
: A SHban olyan átmenet, mely során a stabilból stabilba való átmenet során több kódbit változik meg. | |||
;618 Mi az a kritikus versenyhelyzet? | |||
: Amikor olyan versenyhelyzet jön létre, melynél a több bit változása során illegális állapotátmenet jön létre, melytől a rendszer lefagy. (megjegyzem: lefagyni a Windows szokott. Ez így nem jó kifejezés. wachag) | |||
Ha TSH, akkor lehetséges, hogy információt vesztünk, ha NTSH, akkor megeshet, hogy beragad egy illegális állapotban. | |||
;619 Milyen módszereket ismer a kritikus versenyhelyzet elkerülésére? | |||
: Kódoljunk versenyhelyzet mentesen, vagyis minden stabil-stabil átmenetnél a kódok H-távolsága legyen 1. | |||
: Ha van versenyhelyzet, az ne legyen kritikus, tehát olyat tervezzünk csak be, ami nem kritikus. | |||
: Állapotátvezetés | |||
;620 Mire jó az "állapotátvezetés"? | |||
: Közbeiktatunk instabil állapotot, hogy a kódolás 1 H-távolságú legyen, így minden versenyhelyzet kiküszöbölhető. | |||
[[Kategória:Infoalap]] | |||
A lap jelenlegi, 2018. december 3., 15:13-kori változata
Nem győzöm gyakorlatokon mondani, hogy az itt következő anyagokkal módjával bánjatok. Belenéztem, pár hibás-bizonytalan részt megjelöletem, de nem egy életbiztosítás ebből tanulni, sokatok kisZH-ja ezen bukik el. Nem győzzük azt, hogy egy olyan anyagot nézzünk át/javítsunk folyamatosan, ami közösségi szerkesztésű (meg hát tulajdonképpen van jegyzet :-) ), szóval legyetek óvatosak! Ha valamit nem értesz, inkább kérdezz tőlünk, dolgunk, hogy segítsünk. -- Wacha Gábor, gyakvez
1. Ellenőrző kérdések
- 101 Mi korlátozza az „analóg elvű” feldolgozó egységekből kialakítható rendszer méreteit?
- A csatornába beszűrődő zaj: Távolsági átvitel során a jelhez zaj adódik, amelyet a távolsági közvetítés során használt erősítő felerősít. Analóg egységenként ~0.1% zaj keletkezik.
- 102 Mi korlátozza a „digitális elvű” feldolgozó egységekből kialakítható rendszer méreteit?
- A p-faktor (megbízhatósági faktor), mely megadja, hogy az alkatrész mekkora valószínűséggel romlik el. Általában:
- 103 Milyen feladatai lehetnek a „kódoló egységnek”?
- forráskódolás (tömörítés), csatornakódolás, titkosítás
- 104 Milyen rossz tulajdonságai lehetnek a „csatornának”?
- zaj, támadhatóság, költséges
- 105 Mi a „forráskódolás” célja?
- Célja az információ tömörítése (pl. analóg (végtelen) jel digitalizálása (véges adatok)). Egy jelhez egy kódszó rendelése.
- 106 Mikor mondjuk egy kódkészletről, hogy megfejthető?
- Egy kód megfejhető, ha a kódszavaiból előállított tetszőleges üzenet egyértelműen felbontható a kód kódszavaira. Ha minden kódszóból visszanyerhető az eredeti információ (pl. prefix kódok (pl. fix hosszuságú kód), végkarakteres kód)
- 107 Mi a prefix kód?
- A lehetséges kódszavak közül egyik sem folytatása a másiknak.
- 108 Melyik kódolási módszert nevezzük „optimálisnak”?
- Huffman kódolást
- 109 Hogyan kell kiszámolni az „átlagos kódhosszt”?
- , ahol p az előfordulási valószínűség, l a kódszóhossz
- 110 Hogyan kell kiszámolni egy forrás „entrópiáját”?
- , ahol p a bekövetkezés valószínűsége
- 111 Mi az a „forráskiterjesztés” és mi a célja?
- Kettő vagy több esemény egy eseményként kezelése. Célja a kód optimalizálása.
- 112 Mennyi a „veszteségmentes tömörítés” alsó határa?
- Az entrópia.
- 113 Mennyi a „veszteséges tömörítés” alsó határa?
- Nincs alsó határa, maximum elveszítjük az összes adatot.
- 114 Mi a „folt hiba” és mi a „véletlen hiba”?
- Folt hiba: átvitel során több egymás utáni hiba. Véletlen hiba: átvitel során véletlenül, nem egymás után bekövetkezett hibák.
- 115 Mi az „eltörlődéses hiba”?
- Az átvitel során egy bit törlődik, de a hibát észreveszi a vevő.
- 116 Mi az „átállítódásos hiba”?
- Az átvitel során egy bit értéke invertálódik.
- 117 Milyen hibavédelmi stratégiákat ismer?
- paritásbit
- ismétléses kód
- Hamming-kód (többszörös paritásbit a kódszó bitcsoportjaira)
- többszörös elküldés
- 118 Egy Hamming távolságú kód mire használható eltörlődéses csatornánál?
- Hibajelzésre n hosszig, hibajavításra hosszig.
- 119 Egy Hamming távolságú kód mire használható átállítódásos csatornánál?
- Hibajelzésre hosszig, hibajavításra alsó egészrészéig
- 120 q elemű abc-ből képzett k hosszúságú információt akarunk védeni paritáskóddal. Milyen hosszú lesz a kód, mekkora lesz a Hamming távolsága és hogyan kell megkonstruálni a redundáns részt?
- k+1 hosszúságú lesz a kód. Az ABC minden eleméhez hozzárendelünk egy számot. Előre eldöntjük, hogy az összegük páratlan vagy páros lesz a teljes kódszóban és az alapján teszünk a kódszó végére redundáns részt. A Hamming-távolság 2.
- 121 Mennyi a Hamming kód Hamming távolsága és milyen hibavédelemre használható?
- H=3, Egy hiba javítására alkalmas, vagy két hiba jelzésére.
- 122 Milyen számábrázolási módszereket tanultunk?
- előjeles abszolútértékes
- egyes komplemens
- kettes komplemens
- offszet
- 123 Írja fel 5 biten a decimális +9 és -9 értékeit a tanult számábrázolásokban!
| Számábrázolás | +9 | -9 |
| Előjeles abszolút értékes | 01001 | 11001 |
| Egyes komplemens | 01001 | 10110 |
| Kettes komplemens | 01001 | 10111 |
| Offszet | 11001 | 00111 |
- 124 Milyen tulajdonságú kódokat nevezünk „pozíciókódnak”?
- Az egymásután következő pozíciók kódjának Hamming-távolsága egy.
- 125 Milyen pozíciókódokat ismer és n biten hány pozíció kódolható velük?
- Gray-kód: n biten pozíció. Generálása rekurzív módon, tükrözéses módszerrel történik.
- Johnson-kód: n biten 2n pozíció
2. Ellenőrző kérdések
- 201 Írja fel a Boole algebra kommutativitási axiómáit
- 202 Írja fel a Boole algebra disztributivitási axiómáit!
- 203 Mi a Boole algebrában a dualitás elve?
- A 0-ák és 1-ek valamint a VAGY és ÉS műveletek felcserélhetőek.
- 204 Írja fel a DeMorgan azonosságot!
- 205 Írja fel a Boole algebra negálás műveletét meghatározó definíciót!
- Minden esetén létezik olyan , hogy:
- 206. Elnyelési tulajdonság
- , illetve a dualitás elve miatt
- 207. Írja fel a Boole algebrában a konstanssal való műveletek eredményeit (A.0, A.1,A+0, A+1)!
- 208 Hány különböző n változós logikai függvény van ?
- 209 Mi az a diszjunktív algebrai normál alak?
- Szorzatok összege (ÉSek VAGYa)
- 210 Mi az a konjunktív algebrai normál alak?
- Összegek szorzata (VAGYok ÉSe)
- 211 Melyek a kétváltozós szimmetrikus logikai függvények (amelyek nem változnak, ha a két változót felcseréljük)
- ÉS, VAGY, XOR, NAND (not and), NOR (not or), ekvivalencia (not xor)
- 212 Rajzolja fel és peremezze az ABCD változókra a a Karnaugh táblát és jelölje be az minterm helyét!
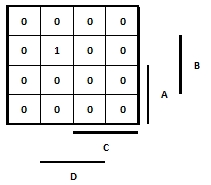
- 213 Rajzolja fel az függvényt Karnaugh táblán!
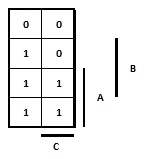
- 214 Rajzolja fel az függvényt igazságtáblában.
| A | B | C | |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
- 215 Mi az a minterm és mi az a maxterm?
- Diszjunktív normál alaknál az egyes tagok az igazságtábla 1-eseit valósítják meg, ezek a mintermek.
- Konjunktív normál alaknál az egyes tagok az igazságtábla 0-áit valósítják meg, ezek a maxtermek.
- 216 Kombinációs hálózatok milyen leírási formáit ismeri?
- Szöveges, algebrai kifejezés, igazság-táblázat, kapcsolási rajz (szimbólumokkal)
- 217 A Boole algebra alapműveleteinek mik a megfelelői a halmazalgebrában?
- ÉS = metszet
- VAGY = unió
- NEM = komplementer/negát
- 218 A Boole algebra alapműveleteinek mik a megfelelői a kapcsoló algebrában?
- ÉS = soros
- VAGY = párhuzamos
- NEM = fordított kapcsoló
- 219 Milyen elnevezéseit ismeri még a mod2 () műveletnek?
- kizáró VAGY (exclusive OR, EXOR, XOR)
- antivalencia
- 220 Melyek azok a kétváltozós műveletek, amelyek Karnaugh táblájában két darab 1-es van?
- XOR /antivalencia/
- XNOR /ekvivalencia/
- 221 Melyek azok a kétváltozós műveletek, amelyek Karnaugh táblájában egy darab 1-es van?
- AND
- NOR
- 222 Rajzolja fel az AND, OR, NAND, NOR kapuk kapcsolási szimbólumait egy választott szabvány szerint! Melyik szabványt választotta?
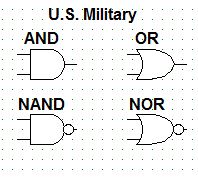
- 223 Mire jó az előadáson tanult teljes összeadó? Írja fel logikai függvényeit!
- Két darab 1 bites szám összeadására alkalmas.
3. Ellenőrző kérdések
- 301 Mi a don't care kombináció?
- Valamely minterm esetén lényegtelen az eredmény.
- 302 Miért lehet egy kombinációs hálózat specifikációjában don't care minterm?
- vagy azért mert a bemeneten soha nem történik meg.
- vagy azért mert ha igen, akkor nincs hatása a kimeneten.
- 303 Rajzoljon fel egy vízszintes elrendezésű öt változós K táblát és peremezze az ABCDE változókkal a szokásos sorrendben!
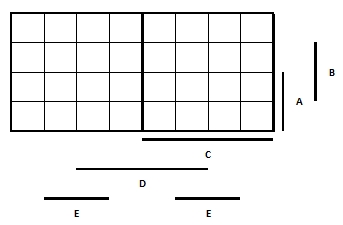
- 304 Jelölje be egy K táblába az mintermet!

- 305 Jelölje be egy K táblába az (A+/B+/C) maxtermet!
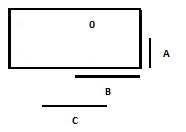
- 306 Jelölje be egy K táblába az A./C primimplikánst!
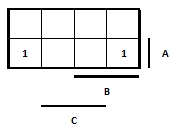
- 307 Jelölje be egy K táblába az (A+/C) primimplikánst!
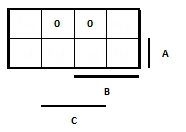
- 308 Rajzolja be egy K táblába az F = A.B + /A.C függvényt!
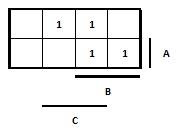
- 309 Rajzolja be egy K táblába az F = [(A mod2 B) + A./C] függvényt!
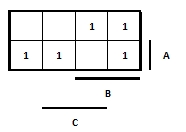
- 310 Rajzolja be egy K táblába az F = A.B + A./C + B./C függvényt!
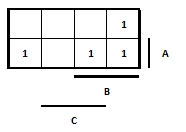
- 311 Mi az a lényeges prímimplikáns?
- Olyan term, amelyből nem hagyható el több változó vagyis nem egyszerűsíthető tovább. Azon prímimplikánsokat, melyek legalább egy megkülönböztetett mintermet tartalmaznak, lényeges prímimplikánsoknak hívjuk.
- 312 Mire jó a lefedési tábla?
- Megtudhatjuk a segítségével, hogy melyik pirimimplikánsokat hagyhatjuk el a függvény megvalósításához, ezzel olcsóbbá téve a kapcsolást.
- 313 Mi a több kimenetű logikai függvények minimalizálásának alapelve?
- A több függvényben is előforduló (azonos) prímimplikánsokat csak egyszer valósítjuk meg.
- 314 Mik a tanult minimalizálási módszer korlátjai?
- Csak 2 szintű diszjunktív vagy konjunktív alakban megadott hálózatokat lehet vele minimalizálni
- 315 Mire optimalizál a tanult minimalizálási módszer?
- a bemenetek számára
- 316 Milyen a több szintű ÉS-VAGY típusú hálózat?
- A többszintü ÉS-VAGY hálozatokban csak ÉS és VAGY kapu található, szintenként egyfajta, egymást váltva.
A következőkhöz azért lenne hozzáfűzésem:
Felmerül bennem a kérdés, hogy a NOT az NAND (vagy NOR) kapu-e... Elfogadtam kisZH-ban, de jobban örültem, amikor valaki a NOT-ot is NAND-dal vagy NOR-ral valósította meg (Wacha Gábor)
--Halftome (vita) 2013. november 5., 19:38 (UTC) A "NOT", az egy inverter. Ha NAND vagy NOR kapunak a bemeneti lábait összekötjük, egy egyszerű invertert kapunk.
- 317 Valósítsa meg az F = A.B függvényt csak NAND kapuval!
- NOT (A NAND B)
- 318 Valósítsa meg az F = A+B függvényt csak NAND kapuval!
- NOT A NAND NOT B
- 319 Valósítsa meg az F = A.B függvényt csak NOR kapuval!
- NOT A NOR NOT B
- 320 Valósítsa meg az F = A+B függvényt csak NOR kapuval!
- NOT (A NOR B)
- 321 Milyen hazárd-típusokat tanultunk?
- dinamikus, statikus , funkcionális
- 322 Mi az a statikus hazárd?
- A kimenet a változás után ugyanolyan értékű lenne, mint előtte, de a késleltetéstől függően rövid ideig a kimenet átvált (0-ról 1-re vagy 1-ről 0-ra) (“szőrös lesz”) majd beáll a kívánt állapot.
(Ezt a "szőrős lesz"-t kérlek, ne írjátok -- Wacha Gábor)
- 323 Mi a az a dinamikus hazárd?
- A kimenet szomszédos BEMENETI változás után át váltana (0->1 vagy 1->0), de a késleltetéstől függően rövid ideig ide-oda váltogat, majd beáll a kívánt állapot.
- 324 Mi az a funkcionális hazárd?
- Egyszerre több bemenet változik meg (jellegre lehet olyan mint a statikus vagy a dinamikus hazárd)
- 325 ÉS-VAGY típusú hálózatokban mi a statikus hazárd feltétele?
- legalább két szintű hálózat + egy változó több úton juthat kimenetre
- 326 ÉS-VAGY típusú hálózatokban mi a dinamikus hazárd feltétele?
- legalább három szintű hálózat és statikus hazárd alacsonyabb szinten
- 327 ÉS-VAGY típusú hálózatokban mi a hazárd kiküszöbölésének módja?
- Hazárdmentesítő primimplikánsok használata
- És ez mit jelent? Egészítsétek már ki... (Wacha Gábor)
- Olyan prímimplikánsokat realizálunk szomszédos hurkok között, melyek nincsenek átfogó lefedéssel kezelve vagy jelút érzékenyítés alapján.
4. Ellenőrző kérdések
- 401 Rajzoljon olyan kapcsolást, amelyik egy jel felfutó éléből impulzust csinál!
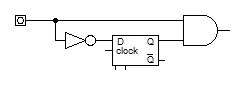
- 402 Rajzoljon olyan kapcsolást, amelyik egy jel lefutó éléből impulzust csinál!
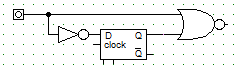
- 403 Rajzoljon olyan kapcsolást, amely egy jel fel- és lefutó éléből is impulzust csinál!
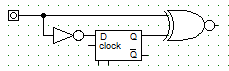
- 404 Mit nevezünk egy függvényrendszer lezártjának?
- A függvényrendszer függvényeinek ismételt alkalmazásával előállítható függvények halmazát (függvények változóiba behelyettesítünk függvényeket)
- 405 Mi az a "funkcionálisan teljes" függvényrendszer?
- F függvényhalmazra funkcionálisan teljes fv.rendszer f, ha f lezártja F ([f] = F). (a lezárás inverz művelete, a függvények bázisait adja)
- 406 Írjon két példát az "összes Boole függvény" funkcionálisan teljes függvényrendszerére!
- + , NOT
- . , NOT
- + , NOT
- NAND
- NOR
- XOR , 1
- 407 Mi ütemezi a szinkron sorrendi hálózat állapotváltozásait?
- Az órajel
- 408 Mi ütemezi az aszinkron sorrendi hálózat állapotváltozásait?
- Visszacsatoló ágalban Y periodikusan nyitjuk zárjuk a kapcsolókat
- 409 Írja fel a Mealy-modell működését leíró egyenleteket!
- 410 Írja fel a Moore-modell működését leíró egyenleteket!
- 411 Jellemezze szavakban a Mealy-modellt!
A kimenet az aktuális állapot és az aktuális bemenet függvénye.
- 412 Jellemezze szavakban a Moore-modellt!
- A kimenet csak az aktuális állapottól függ.
- 413 Rajzolja fel a Mealy-modell blokkvázlatát!
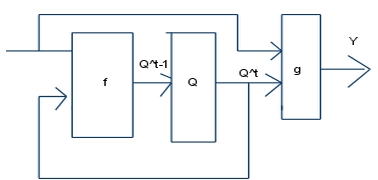
- 414 Rajzolja fel a Moore-modell blokkvázlatát!
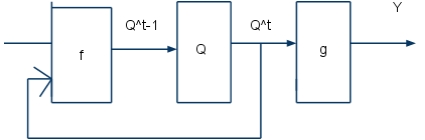
- 415 Mi jellemzi a szinkron sorrendi hálózatot?
- A szinkron sorrendi hálózat állapotait memória tulajdonságú alkatrészek (flip-flopok) tárolják, egy órajellel ütemezett időpontokban.
- 416 Rajzolja fel egy D FF állapotgráfját!
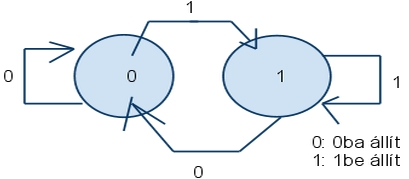
- 417 Rajzolja fel egy T FF állapotgráfját!
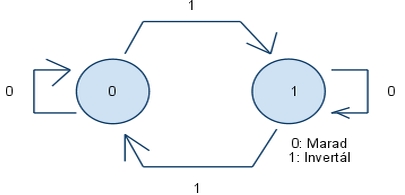
- 418 Rajzolja fel egy JK FF állapotgráfját!
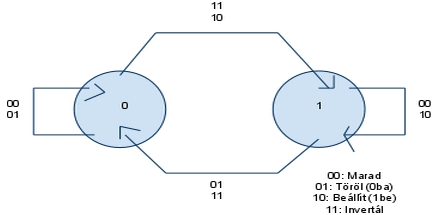
- 419 Írja fel egy D FF vezérlési egyenletét!
- 420 Írja fel egy T FF vezérlési egyenletét!
- 421 Írja fel egy JK FF vezérlési egyenletét!
- 422 Rajzolja fel egy D FF állapotátmeneti tábláját!
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- 423 Rajzolja fel egy T FF állapotátmeneti tábláját!
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 424 Rajzolja fel egy JK FF állapotátmeneti tábláját!
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
VAGY
| Qt | J=0 | J=1 | ||
| K=0 | K=1 | K=0 | K=1 | |
| a | a/0 | a/0 | b/1 | b/1 |
| b | b/1 | a/0 | b/1 | a/0 |
- 425 Csináljon JK FF-ból T FF-ot!
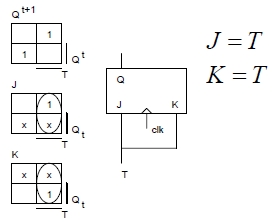
- 426 Csináljon JK FF-ból D FF-ot!
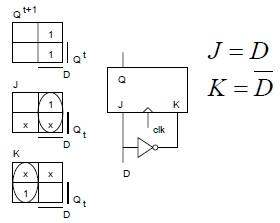
- 427 Mit csinál az RS FF a különböző vezérlések mellett?
- 00 - marad
- 01 - 1-be állít
- 10 - 0-ba állít
- 11 - TILOS
- 428 Mit csinál a JK FF a különböző vezérlések mellett?
- 00 - marad
- 01 - 0-ba állít
- 10 - 1-be állít
- 11 - invertál
- 429 Rajzoljon fel egy 3 bites szinkron bináris felfelé számlálót!
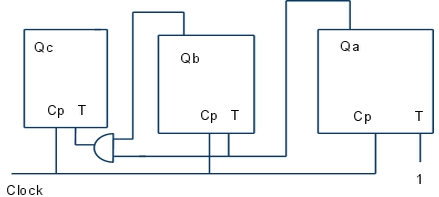
- 430 Rajzoljon fel egy 3 bites shiftregisztert!
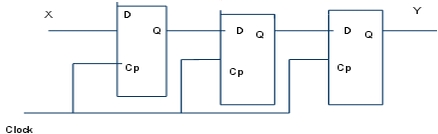
5. Ellenőrző kérdések
- Megjegyezném, hogy ezekben is találtam hibákat, javítsátok. (Azért ti, hogy tanuljatok belőle, ez ilyen oktatói hülyeség). WachaG
- 501 Mik jellemzik a TSH hálózatokat?
- Egy automata teljesen specifikált (TSH), ha az összes következő állapota (Qt+1) és kimenete (Y) specifikált.
- 502 Mik jellemzik az NTSH hálózatokat?
- Van az állapottáblában olyan kimenet vagy következő állapot, ami nem specifikált (tartalmaz don't care-t)
- 503 Milyen állapotminimalizálási módszereket ismer?
- Partíciófinomítás, lépcsős-táblás módszer
- 504 Mi adja a partíciófinomítás első partícióját?
- Megadott bemenetekre eltérő kimenetet adó esetek 1-1 külön csoportot alkotnak.
- 505 Mikor zárt egy particionálás?
- Egy adott partíción belüli állapotokból, adott bemenetre azonos partícióba megyünk.
- 506 Írja fel az állapotekvivalencia rekurzív definícióját!
- , ha bármely lehetséges bemenetre érvényes, hogy a kimenet azonos
Ez megint pontatlan így. (wachag) Egyfelől, mi az a g? Írjátok már oda a kisZH-ba, mert akármivel jelölhetsz akármit... Másfelől meg mit jelent a képlet? Meg mik ezek az indexek? Amik ráadásul hibásak...
- 507 Írja fel az állapotkompatibilitás rekurzív definicióját!
- , ha bármely érvényes bemenetre a specifikált helyeken, hogy és
Megint: mi az a g és mi az az f? Miért ne írhatná valaki ezt:
- , ha bármely érvényes bemenetre a specifikált helyeken, hogy és
Ennek is van értelme, de ugyanúgy nem derül ki belőle semmi. (wachag) Arról már nem is beszélve, hogy az indexek megint nem stimmelnek...
- 508 Mi jellemzi a maximális ekvivalencia osztályozást?
- Az egyes osztályok nem bővíthetőek új állapottal. Minden állapot benne van 1 osztályban, és ezek páronként ekvivalensek.
- 509 Mi jellemzi a maximális kompatibilitási osztályozást?
- Nincs több olyan állapot, ami az osztály összes tagjával kompatibilis lenne. 1 osztály állapotai páronként kompatibilisek, és maximális nagyságúak.
- 510 Egy állapot hány helyen lehet a max. kompatibilitási osztályozásban?
- Annyi helyen lehet, ahány olyan osztály van, melynek minden tagjával kompatibilis. Ez akár az összes kompatibilitási osztály is lehet.
- 511 Milyen hálózatokhoz javasoljuk a partíciófinomítást?
- TSH
- 512 Milyen hálózatokhoz javasoljuk a lépcsős táblás módszert?
- TSH, NTSH
- 513 Fogalmazza meg a szomszédos kódolás feltételét a "soronkövetkező állapotok" alapján!
- Ha van olyan lehetséges bemenet (), hogy a két állapot () soronkövetkező állapota azonos, akkor az ezek közti Hamming-távolság () legyen 1.
- Legyen , ha -re .
- 514 Fogalmazza meg a szomszédos kódolás feltételét a "megelőző állapotok" alapján!
- Ha soronkövetkező állapota -nek, akkor Hamming-távolságuk legyen 1.
- Legyen , ha -re és .
- 515 n biten M állapotnak hányféle "különböző költségű" állapotkódolása van?
- 516 Milyen átalakításokkal biztosan nem változik egy állapotkódolás költsége?
- A kódbitek átnevezésével vagy invertálásával.
- 517 Mit jelent az, hogy "előírt kimenet alapján" kódolunk?
- Adott bemeneti kombinációra azonos kimenetet adó állapotok kódját úgy választjuk meg, hogy egy bitben térjenek el(Hamming-távolságuk 1 legyen).
- 518 Miket nevezünk önfüggő szekunder változóknak?
- Olyan állapotcsoportot, amiben a következő értékek csak a csoporton belüli változóktól függ, a csoporton kívüli állapotoktól nem. Például:
- Két állapot:
- És ,
- Ekkor egy önfüggő szekunder változócsoportot alkot, mert más változótól nem függ. -re ez nem igaz, mert függ -tól.
- együtt önfüggő szekunder változócsoportot alkot, hisz nem függnek a csoporton kívüli változótól (itt nincs is több változó, ez triviális).
- 519 Milyen triviális HT particiókat ismer?
- Ha minden állapot 1 db osztályban van, és ha minden állapot külön-külön osztályban van.
Ez így szerencsétlen megfogalmazás. "vagy ha minden". wachag
- 520 Mi jellemzi a HT particionálás osztályait?
- Helyettesítési tulajdonságú partíció. az osztályok zártak, ha kimenet nem vesszük figyelembe. Egy osztály minden állapotából, adott bemenet hatására, egy adott osztály valamelyik állapotába jutunk.
- 521 Mikor zárt egy HT particionálás?
- Ha egy osztály minden átmenete azonos osztályba megy át.
- 522 Mikor alakul ki a hálózat párhuzamos dekompoziciója?
- Két ortogonális HT partíció alapján kódolva, párhuzamos dekompozíció alakul ki.
- 523 Mikor alakul ki a hálózat soros dekompoziciója?
- Egy HT partíció alapján kódolva soros dekompozíció alakul ki.
- 524 Mikor ortogonális két HT particionálás?
- Amikor partíciók blokkjainak metszete maximum 1 állapotot tartalmaz és az összes állapot szerepel benne, vagyis ortogonálisak.
- 525 Milyen HT particiót talál "ciklikus" feladatokban?
- Ortogonálist.
6. Ellenőrző kérdések
- 601 Milyen okai vannak az órajelcsúszásnak?
- Eltérő futási idők, eltérő komparálási szint, eltérő meghajtó.
- 602 Milyen hibákat okozhat az órajelcsúszás?
- Ha az órajelcsúszás nagyobb mint a biztonsági idő, akkor a flipflopok különböző állapotok alapján vesznek mintát, és nem megfelelő állapotba váltanak.
- 603 Hogyan küszöbölhető ki az órajelcsúszás okozta hiba?
- A Master-Slave elvvel, azaz a biztonsági idő meghosszabbításával.
- 604 Master-Slave FF-nál melyik fokozat adja kimenetet?
- A slave
- 605 Rajzoljon fel D FF-okból egy kettős élvezérelt MS FF-ot!
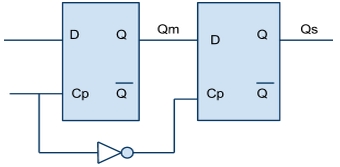
- 606 Rajzoljon fel egy kettős élvezérelt JK MS-FF-ot!
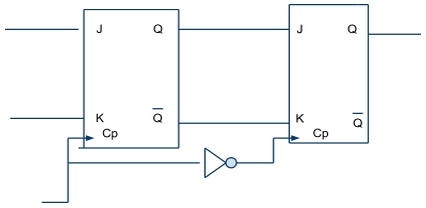
- 607 Mi ütemezi az aszinkron sorrendi hálózat állapotváltozását?
- A bemenet változása.
- 608 Miben különbözik az aszinkron sorrendi hálózat a szinkrontól?
- A szinkron hálózatokban minden órajel vezérelt, míg az aszinkronban a bemeneti jelek megváltozásától függ a rendszer állapota
- 609 Mik az FMA feltételek (alapvető működésű aszinkron hálózat feltételei)?
- 1. egyszerre 1 időpillanatban csak 1 bemenet változik (a bemeneten csak 1 Hamming-távú változás)
- 2. újabb változás csak akkor lehetséges, ha az előző bemenetváltásból következő átmeneti állapot már lezajlott (csak stabil állapotban történik bemeneti változás)
- 610 Rajzolja fel egy aszinkron /R/S FF kapcsolását!
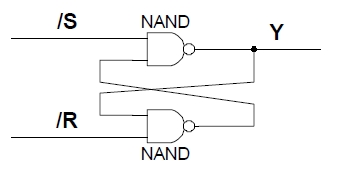
- 611 Rajzolja fel egy aszinkron RS FF kapcsolását!
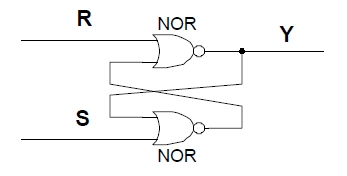
- 612 Hogyan kell vezérelni az aszinkron /R/S FF-ot ahhoz, hogy a különböző állapotátmeneteket megvalósíthassuk?
| 0 | 0 | - | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | - |
- 613 Hogyan kell vezérelni az aszinkron RS FF-ot ahhoz, hogy a különböző állapotátmeneteket megvalósíthassuk?
| R | S | ||
| 0 | 0 | - | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | - |
- 614 Hogyan működik az aszinkron DG FF?
- Ha G=0, akkor az FF nincs engedélyezve, és a régi állapotra emlékszik.
- Ha G=1, akkor az FF engedélyezve van, és a D-n levő értéket beírja magába, mint új állapot.
- 615 Hogyan kell vezérelni az aszinkron DG FF-ot ahhoz, hogy a különböző állapotátmeneteket megvalósíthassuk?
| D | G | ||
| 0 | 0 | - | 0 |
| 0 | 1 | ||
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | - | 0 |
| 1 | 1 |
- 616 Mi jellemzi az előzetes (primitív) állapottáblát?
- Minden sorban csak 1 stabil állapot van.
- 617 Mi az a versenyhelyzet?
- A SHban olyan átmenet, mely során a stabilból stabilba való átmenet során több kódbit változik meg.
- 618 Mi az a kritikus versenyhelyzet?
- Amikor olyan versenyhelyzet jön létre, melynél a több bit változása során illegális állapotátmenet jön létre, melytől a rendszer lefagy. (megjegyzem: lefagyni a Windows szokott. Ez így nem jó kifejezés. wachag)
Ha TSH, akkor lehetséges, hogy információt vesztünk, ha NTSH, akkor megeshet, hogy beragad egy illegális állapotban.
- 619 Milyen módszereket ismer a kritikus versenyhelyzet elkerülésére?
- Kódoljunk versenyhelyzet mentesen, vagyis minden stabil-stabil átmenetnél a kódok H-távolsága legyen 1.
- Ha van versenyhelyzet, az ne legyen kritikus, tehát olyat tervezzünk csak be, ami nem kritikus.
- Állapotátvezetés
- 620 Mire jó az "állapotátvezetés"?
- Közbeiktatunk instabil állapotot, hogy a kódolás 1 H-távolságú legyen, így minden versenyhelyzet kiküszöbölhető.
