„Fizika 2 - Ellenőrző kérdések és válaszok” változatai közötti eltérés
a autoedit v2: fájlhivatkozások egységesítése, az új közvetlenül az adott fájlra mutat |
|||
| (8 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
{{vissza|Fizika 2}} | |||
Ez az oldal a [[Fizika 2]] tárgyhoz kapcsolódó elméleti kérdések-válaszok gyűjteménye! A ''Hudson-Nelson'' könyv fejezeteinek a végén található ellenőrző kérdések közül azok vannak itt, amiket az előadók megoldásra javasoltak. | Ez az oldal a [[Fizika 2]] tárgyhoz kapcsolódó elméleti kérdések-válaszok gyűjteménye! A ''Hudson-Nelson'' könyv fejezeteinek a végén található ellenőrző kérdések közül azok vannak itt, amiket az előadók megoldásra javasoltak. | ||
| 8. sor: | 10. sor: | ||
A ZH-kon és a vizsgákon lényegében ezen ismeretek számonkérése történik. A vizsga harmadik része 5 db. szöveges kifejtést igénylő kérdést tartalmaz, amelyek a ebből kérdésgyűjteményből valók. | A ZH-kon és a vizsgákon lényegében ezen ismeretek számonkérése történik. A vizsga harmadik része 5 db. szöveges kifejtést igénylő kérdést tartalmaz, amelyek a ebből kérdésgyűjteményből valók. | ||
<div class="noautonum">__TOC__</div> | |||
__TOC__ | |||
| 652. sor: | 653. sor: | ||
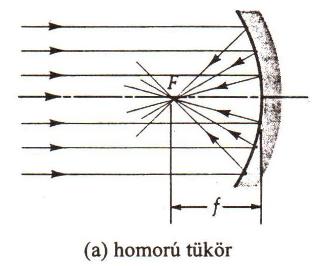
===A05. Homorú tükör képalkotásának sugármenete=== | ===A05. Homorú tükör képalkotásának sugármenete=== | ||
[[ | [[File:Fizika2 segédlet Homorútükör.jpg]] | ||
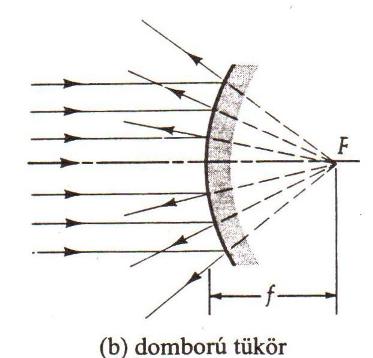
===A06. Domború tükör képalkotásának sugármenete=== | ===A06. Domború tükör képalkotásának sugármenete=== | ||
[[ | [[File:Fizika2 segédlet Domborútükör.jpg]] | ||
==XXXVII. Fejezet== | ==XXXVII. Fejezet== | ||
| 697. sor: | 698. sor: | ||
===B01. A fehér fény diszperziója prizmán, sugármenet.=== | ===B01. A fehér fény diszperziója prizmán, sugármenet.=== | ||
[[ | [[File:Fizika2 segédlet Diszperzió.jpg]] | ||
===B02. A szivárvány kialakulása=== | ===B02. A szivárvány kialakulása=== | ||
| 732. sor: | 733. sor: | ||
===A05. A Michelson-féle interferometer=== | ===A05. A Michelson-féle interferometer=== | ||
[[ | [[File:Fizika2 segédlet Michelson interferométer.jpg]] | ||
| 756. sor: | 757. sor: | ||
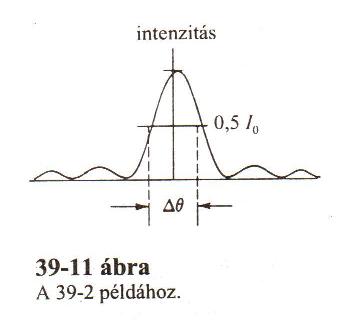
===A05. Egyetlen rés (Fraunhofer) diffrakciójának intenzitás görbéje (rajz).=== | ===A05. Egyetlen rés (Fraunhofer) diffrakciójának intenzitás görbéje (rajz).=== | ||
[[ | [[File:Fizika2 segédlet Egyreses intenzitas.jpg]] | ||
===A06. A felbontóképesség Rayleigh-féle kritériuma.=== | ===A06. A felbontóképesség Rayleigh-féle kritériuma.=== | ||
| 856. sor: | 857. sor: | ||
==XLII. Fejezet== | ==XLII. Fejezet== | ||
===A01. Rajzolja fel, a fekete test spektrális energiasűrűségét megadó ábrát.=== | |||
=== | |||
1021 oldal 42-2 ábra. | 1021 oldal 42-2 ábra. | ||
=== | ===A02. Adja meg a Stefan-Boltzmann féle törvényt=== | ||
Ahol R az emittancia, vagyis a fekete test által egységnyi idő alatt egységnyi felületen, valamennyi hullámhosszán kisugárzott energia. T abszolút hőmérséklet. <math> \sigma </math>= Stefan-Boltzmann állandó. | Ahol R az emittancia, vagyis a fekete test által egységnyi idő alatt egységnyi felületen, valamennyi hullámhosszán kisugárzott energia. T abszolút hőmérséklet. <math> \sigma </math>= Stefan-Boltzmann állandó. | ||
<math> R = \sigma T^4 </math> | <math> R = \sigma T^4 </math> | ||
=== | ===A03. Mit nevezünk „ultraibolya” katasztrófának=== | ||
A Rayleigh-Jeans sugárzási törvény: jól illeszkedik nagyon nagy hullámhosszon végzett mérésekhez. Másutt mindenütt drasztikus eltérés mutatkozik a mérési eredményekhez képest. Ez az eltérés a rövidhullámhosszoknál volt a legjelentősebb, ezért nevezik ultraibolya katasztrófának. | A Rayleigh-Jeans sugárzási törvény: jól illeszkedik nagyon nagy hullámhosszon végzett mérésekhez. Másutt mindenütt drasztikus eltérés mutatkozik a mérési eredményekhez képest. Ez az eltérés a rövidhullámhosszoknál volt a legjelentősebb, ezért nevezik ultraibolya katasztrófának. | ||
=== | ===A04. Adja meg a harmonikus oszcillátor Planck-féle (energia)kvantálási törvényét=== | ||
ahol h a Planck állandó | ahol h a Planck állandó | ||
<math> E_{megengedett} = nhf </math> | <math> E_{megengedett} = nhf </math> | ||
=== | ===A05. Ismertesse a fényelektromos jelenséget (csak a kísérletet és annak eredményét!)=== | ||
Fény hatására elektronok lépnek ki az elektródából. | Fény hatására elektronok lépnek ki az elektródából. | ||
A kísérlet: 42-7es ábra, 1028. oldal | A kísérlet: 42-7es ábra, 1028. oldal | ||
eredménye: a kilépő elektronok kinetikus energiája nem függ a fény intenzitásától, csak a fény frekvenciájától. Van egy küszöbfrekvencia, ami alatt nem jelenik meg fotoelektron. Nem figyeltek meg késési időt abban az esetben, ha gyengébb fénnyel világítottak, ahhoz képest, amikor erősebbel. | eredménye: a kilépő elektronok kinetikus energiája nem függ a fény intenzitásától, csak a fény frekvenciájától. Van egy küszöbfrekvencia, ami alatt nem jelenik meg fotoelektron. Nem figyeltek meg késési időt abban az esetben, ha gyengébb fénnyel világítottak, ahhoz képest, amikor erősebbel. | ||
=== | ===A06. Ismertesse a fényelektromos jelenség Einstein-féle magyarázatát=== | ||
Az f frekvenciájú sugárzás emissziója és abszorpciója mindig kvantumok (fotonok) formájában történik, amelyek energiája E=h*f. a foton a térben lokalizált és a forrástól c sebességgel távolodik. az anyagból akkor tud kilépni elektron ha legyőzi a kilépési munkát a fenn maradó rész pedig mozgási energia lesz -> h*f = Kmax + Wo | Az f frekvenciájú sugárzás emissziója és abszorpciója mindig kvantumok (fotonok) formájában történik, amelyek energiája E=h*f. a foton a térben lokalizált és a forrástól c sebességgel távolodik. az anyagból akkor tud kilépni elektron ha legyőzi a kilépési munkát a fenn maradó rész pedig mozgási energia lesz -> h*f = Kmax + Wo | ||
=== | ===A07. Vázolja fel egy fotocella szerkezeti felépítését=== | ||
=== | ===A08. Ismertesse a Compton effektust=== | ||
Vékony szénlapra monokromatikus röntgensugár nyalábot irányított és megfigyelte, hogy a lapról különböző szögben szórt röntgen sugarak <math> \lambda </math>’ hullámhossza nagyobb, mint a beeső sugarak <math> \lambda_0 </math> hullámhossza. A <math> \Delta\lambda = \lambda' - \lambda_0 </math> hullámhossz eltolódás végül a céltárgy anyagától függetlennek bizonyult, tehát a jelenség az elektronnal kapcsolatos. A folyamatban a foton kezdetben nyugalomban lévő elektronnal részecskeszerűen ütközik, így szórt foton és szórt elektron keletkezik. Ebből az következik, hogy a fotonnak impulzusa van, és a folyamat kísérlet során teljesült az impulzusmegmaradás törvénye: | Vékony szénlapra monokromatikus röntgensugár nyalábot irányított és megfigyelte, hogy a lapról különböző szögben szórt röntgen sugarak <math> \lambda </math>’ hullámhossza nagyobb, mint a beeső sugarak <math> \lambda_0 </math> hullámhossza. A <math> \Delta\lambda = \lambda' - \lambda_0 </math> hullámhossz eltolódás végül a céltárgy anyagától függetlennek bizonyult, tehát a jelenség az elektronnal kapcsolatos. A folyamatban a foton kezdetben nyugalomban lévő elektronnal részecskeszerűen ütközik, így szórt foton és szórt elektron keletkezik. Ebből az következik, hogy a fotonnak impulzusa van, és a folyamat kísérlet során teljesült az impulzusmegmaradás törvénye: | ||
<math> p_{foton} = \frac{hf}{c} = \frac{h}{\lambda} </math> | <math> p_{foton} = \frac{hf}{c} = \frac{h}{\lambda} </math> | ||
=== | ===A09. Vázolja fel az (optikai) „két réses kísérletet” === | ||
42-15 ábra. | 42-15 ábra. | ||
=== | ===A10. Adja meg a kétréses kísérlet „fotonos” tárgyalását=== | ||
Ha mind a két rés nyitva van, akkor rendes kétréses interferencia képet látunk, azonban ha az expozíciós idő felére az egyik majd a másik rést tartjuk zárva akkor, a kép két egyréses elhajlás szuperpozíciója lesz. Ebből arra a következtetésre jutottak, hogy minden foton csak saját magával interferál. | Ha mind a két rés nyitva van, akkor rendes kétréses interferencia képet látunk, azonban ha az expozíciós idő felére az egyik majd a másik rést tartjuk zárva akkor, a kép két egyréses elhajlás szuperpozíciója lesz. Ebből arra a következtetésre jutottak, hogy minden foton csak saját magával interferál. | ||
===B01. Adja meg a „feketetest” fogalmát=== | |||
===B02. Adja meg a Wien-féle eltolódási törvényt=== | |||
B02. Adja meg a Wien-féle eltolódási törvényt | |||
Az abszolút hőmérséklet emelkedésével a spektrális eloszlás maximumához tartozó hullámhossz a rövidebb hullámok felé tolódik el. | Az abszolút hőmérséklet emelkedésével a spektrális eloszlás maximumához tartozó hullámhossz a rövidebb hullámok felé tolódik el. | ||
lambdam*T=állandó | lambdam*T=állandó | ||
B03. Adja meg a Planck- féle sugárzási törvény matematikai alakját | ===B02. Adja meg a „Rayleigh-Jeans féle sugárzási törvényt=== | ||
===B03. Adja meg a Planck- féle sugárzási törvény matematikai alakját=== | |||
<math> du_ \lambda = f( \lambda , T ) d \lambda = \frac{8 \pi h c \lambda^{-5}}{e^{ h c / \lambda k T } - 1} d \lambda </math> | <math> du_ \lambda = f( \lambda , T ) d \lambda = \frac{8 \pi h c \lambda^{-5}}{e^{ h c / \lambda k T } - 1} d \lambda </math> | ||
===B04. Rajzolja fel a „foto-elektromos áram – alkalmazott feszültség” mérési görbét === | |||
===B05. Adja meg a Compton eltolódást (hullámhosszváltozást) megadó formulát=== | |||
===B06. Mit nevezünk „párkeltésnek”?=== | |||
==XLIII. Fejezet== | ==XLIII. Fejezet== | ||
===A01. A Thoson-féle atommodell=== | |||
=== | |||
Az atom tömegének nagy részét egy Ze pozitív töltésű folyadékgömb tartalmazza. Az elektronok ennek a pozitív folyadéknak a belsejébe vannak beágyazva. "mazsolás puding" | Az atom tömegének nagy részét egy Ze pozitív töltésű folyadékgömb tartalmazza. Az elektronok ennek a pozitív folyadéknak a belsejébe vannak beágyazva. "mazsolás puding" | ||
=== | ===A02. A Rutherford-féle atommodell és hiányosságai=== | ||
Nagy tömegű központi töltés a központi régióban, az úgynevezett atommagban koncentrálódik. | Nagy tömegű központi töltés a központi régióban, az úgynevezett atommagban koncentrálódik. | ||
Mi tartja együtt a mag töltéseit? Mi tartja távol a negatív töltésű elektronokat a pozitívtöltésű atommagtól? | Mi tartja együtt a mag töltéseit? Mi tartja távol a negatív töltésű elektronokat a pozitívtöltésű atommagtól? | ||
=== | ===A03. A Bohr-féle atommodell és posztulátumai=== | ||
# Az elektron a proton körül körpályán mozog a klasszikus mechanika törvényei szerint. | # Az elektron a proton körül körpályán mozog a klasszikus mechanika törvényei szerint. | ||
# Az elektronok csak bizonyos megengedett r sugarú pályákon mozoghatnak, s ezeken nem sugároznak. Minthogy ezeken a pályákon az E energia állandó, az elektron ezeken a pályákon stacionárius állapotban van. | # Az elektronok csak bizonyos megengedett r sugarú pályákon mozoghatnak, s ezeken nem sugároznak. Minthogy ezeken a pályákon az E energia állandó, az elektron ezeken a pályákon stacionárius állapotban van. | ||
| 930. sor: | 925. sor: | ||
# stacionárius állapotom közti átmenetek úgy mennek végbe, hogy az elektron valahogyan átugrik egyik állapotból a másikba. Ekkor az atom elektromágneses hullámokat bocsát ki vagy nyel el. A két energia állapot energiája közti különbség egyenlő a kibocsátott sugárzás energiakvantumával. | # stacionárius állapotom közti átmenetek úgy mennek végbe, hogy az elektron valahogyan átugrik egyik állapotból a másikba. Ekkor az atom elektromágneses hullámokat bocsát ki vagy nyel el. A két energia állapot energiája közti különbség egyenlő a kibocsátott sugárzás energiakvantumával. | ||
===A04. A hidrogén atom energia szintjei [eV]-ban kifejezve === | |||
=== | |||
<math> E_n= \frac{13,6eV}{n^2} </math> | <math> E_n= \frac{13,6eV}{n^2} </math> | ||
=== | ===A05. A (Bohr-féle) „korrespondencia elv”=== | ||
Minden új elméletnek arra a klasszikus elméletre kell redukálódnia, amely megfelel a klasszikus helyzetre illő körülményekre alkalmazva. | Minden új elméletnek arra a klasszikus elméletre kell redukálódnia, amely megfelel a klasszikus helyzetre illő körülményekre alkalmazva. | ||
=== | ===A06. A de-Broglie féle hullámhossz definíciója === | ||
Az elektron az atommag körül állóhummálként van jelen, hullámhossza a De Brogli hullámhossz: | Az elektron az atommag körül állóhummálként van jelen, hullámhossza a De Brogli hullámhossz: | ||
<math> \lambda = \frac{h}{p} </math>, ahol p a részecske impulzusa. | <math> \lambda = \frac{h}{p} </math>, ahol p a részecske impulzusa. | ||
=== | ===A07. A de-Broglie féle (hidrogén) atom modell=== | ||
A hidrogén atommodell Bohr modelljében keringő elektronoknak megfelelő a de-Broglie hullámok állóhullámok. Csomópontok közti távolság lambda / 2. | A hidrogén atommodell Bohr modelljében keringő elektronoknak megfelelő a de-Broglie hullámok állóhullámok. Csomópontok közti távolság lambda / 2. | ||
=== | ===A08. A Davisson-Germer kísérlet és (kvalitatív) eredménye=== | ||
Az elektronok fémfelületekről történő visszaverődést tanulmányozták, ahelyett hogy az elektronok tetszőeges szögben egyenletesen szóródtak volna egyes irányokba több, másokba kevesebb elektron szóródott, a kísérlet eredménye hogy a szokatlan szórásért az anyaghullámok a felelősek. | Az elektronok fémfelületekről történő visszaverődést tanulmányozták, ahelyett hogy az elektronok tetszőeges szögben egyenletesen szóródtak volna egyes irányokba több, másokba kevesebb elektron szóródott, a kísérlet eredménye hogy a szokatlan szórásért az anyaghullámok a felelősek. | ||
=== | ===A09. Az idõtõl független Schrödinger egyenlet (egy dimenzióban)=== | ||
=== | ===A10. A hullámfüggvény Born-féle értelmezése=== | ||
Einstein feltevése, hogy E^2 legyen arányos annak a valószínűségével, hogy az adott hely környezetében egy fotont találunk. Born kiterjesztette a hullámfüggvény értelmezésére azt feltételezte, hogy <math> |\Psi|^2 </math> annak a valószínűsége, hogy a részecske az adott tartományban tartózkodik. P = <math> |\Psi|^2 </math> | Einstein feltevése, hogy E^2 legyen arányos annak a valószínűségével, hogy az adott hely környezetében egy fotont találunk. Born kiterjesztette a hullámfüggvény értelmezésére azt feltételezte, hogy <math> |\Psi|^2 </math> annak a valószínűsége, hogy a részecske az adott tartományban tartózkodik. P = <math> |\Psi|^2 </math> | ||
=== | ===A11. A (1D) dobozba zárt részecske állapotfüggvényeinek grafikus ábrázolása=== | ||
1060. oldal, 43-18 ábra. | 1060. oldal, 43-18 ábra. | ||
=== | ===A12. A (1D) dobozba zárt részecske "megtalálási valószínűség-sűrűség" függvényeinek grafikus ábrázolása=== | ||
43-19 ábra | 43-19 ábra | ||
=== | ===A13. (1D) Dobozba zárt részecske energiaszintjeinek a „n” kvantumszámtól === | ||
<math> E_n = (\frac{h^2}{SmD^2})n^2 </math> | <math> E_n = (\frac{h^2}{SmD^2})n^2 </math> | ||
=== | ===A14. Az alagút effektus jelensége=== | ||
Az elektron hullámfüggvénye be tud hatolni a falba és a fal túloldalán is a zérustól különböző értéket vehet fel. Ez azt jelenti, hogy esetleg úgy találjuk, hogy az elektron egy kvantummechanikai alagúton átjutott a potenciál gáton ahova a klasszikus elmélet szerint sosem juthatott volna. | Az elektron hullámfüggvénye be tud hatolni a falba és a fal túloldalán is a zérustól különböző értéket vehet fel. Ez azt jelenti, hogy esetleg úgy találjuk, hogy az elektron egy kvantummechanikai alagúton átjutott a potenciál gáton ahova a klasszikus elmélet szerint sosem juthatott volna. | ||
=== | ===A15. A Heisenberg-féle határozatlansági összefüggés=== | ||
Egy részecske helyének és impulzusának egyidejű mérésekor a határozatlanságok szorzata nagyobb vagy olyan nagyságrendű, mint a h/2*pi szám. | Egy részecske helyének és impulzusának egyidejű mérésekor a határozatlanságok szorzata nagyobb vagy olyan nagyságrendű, mint a h/2*pi szám. | ||
===B01. A Rutherford-féle szórási kísérlet és eredménye === | |||
===B02. A (Bohr-féle) korrespondencia elv érvényessége hidrogén atom esetén=== | |||
B02. A (Bohr-féle) korrespondencia elv érvényessége hidrogén atom esetén | |||
===B02. Az állapotfüggvény normálása=== | |||
===B03. A (1D) dobozba zárt részecske normált állapotfüggvényei=== | |||
===B04. Az „alagút mikroszkóp” mûködési elve=== | |||
===B05. A Bohr-féle „komplementaritási elv”=== | |||
==XLIV. Fejezet== | ==XLIV. Fejezet== | ||
===A01. Az (idõfüggetlen) 3D Schrödinger-egyenlet Descartes koordináta rendszerben=== | |||
=== | |||
<math> -\frac{\hslash^2}{2m}(\frac{\partial^2\Psi}{\partial x^2} + \frac{\partial^2\Psi}{\partial y^2} + \frac{\partial^2\Psi}{\partial z^2}) + U(x,y,z)\Psi = E_{\Psi} </math><br /> | <math> -\frac{\hslash^2}{2m}(\frac{\partial^2\Psi}{\partial x^2} + \frac{\partial^2\Psi}{\partial y^2} + \frac{\partial^2\Psi}{\partial z^2}) + U(x,y,z)\Psi = E_{\Psi} </math><br /> | ||
<math> U(x,y,z) = -(\frac{1}{4\Pi \varepsilon_0})\frac{e^2}{\sqrt{(x^2+y^2+z^2)}} </math> | <math> U(x,y,z) = -(\frac{1}{4\Pi \varepsilon_0})\frac{e^2}{\sqrt{(x^2+y^2+z^2)}} </math> | ||
=== | ===A02. A hidrogén atom elektronállapotainak általános (szeparált) matematikai alakja=== | ||
=== | ===A03. A (L) perdület nagyságának a kvantálási törvénye=== | ||
l a mellékkvantumszám | l a mellékkvantumszám | ||
<math> L = \hslash \sqrt{l(l+1)} </math> | <math> L = \hslash \sqrt{l(l+1)} </math> | ||
=== | ===A04. A (L) perdület „z” irányú komponensének a kvantálási törvénye=== | ||
m a mágneses kvantumszám | m a mágneses kvantumszám | ||
<math> L = \hslash m_l </math> | <math> L = \hslash m_l </math> | ||
=== | ===A05. A () perdület vektor (!) kvantálásának grafikus szemléltetése=== | ||
1079. oldal 44-3 as ábra | 1079. oldal 44-3 as ábra | ||
=== | ===A06. A Stern-Gerlach kísérlet === | ||
A kísérlet a spin-mégneses momentum beállását demonstrálta a mágneses térben. Semleges ezüst atomokból álló sugarat bocsátottak keresztül inhomogén mágneses téren. Az ezüst atom mágneses momentuma egyetlen vegyérték elektronból származik, amelynek kvantummechanika szerint nincs pálya-mágnesesmomentuma (l = 0), ezért a mágneses momentum csak a spinnek tulajdonítható. A kérdés az, hogy hogy a mégneses téren átlőtt atomnyaláb egy vagy három foltban csapódik az ernyőre (Bohr illetve Sommerfeld törvényei szerint). A várakozásokkal ellentétben 2 jól szétválasztható vonal érkezett, bizonyítva ezzel a spin-mágnesesmomentum térbeli orientációját a mágneses tér hatására. | A kísérlet a spin-mégneses momentum beállását demonstrálta a mágneses térben. Semleges ezüst atomokból álló sugarat bocsátottak keresztül inhomogén mágneses téren. Az ezüst atom mágneses momentuma egyetlen vegyérték elektronból származik, amelynek kvantummechanika szerint nincs pálya-mágnesesmomentuma (l = 0), ezért a mágneses momentum csak a spinnek tulajdonítható. A kérdés az, hogy hogy a mégneses téren átlőtt atomnyaláb egy vagy három foltban csapódik az ernyőre (Bohr illetve Sommerfeld törvényei szerint). A várakozásokkal ellentétben 2 jól szétválasztható vonal érkezett, bizonyítva ezzel a spin-mágnesesmomentum térbeli orientációját a mágneses tér hatására. | ||
=== | ===A07. Az (S) elektron-spin kvantálási törvénye=== | ||
=== | ===A08. A Pauli-féle kizárási elv=== | ||
Egy atomban nem lehet két olyan elektron, amelynek mind a négy kvantumszámaazonos. | Egy atomban nem lehet két olyan elektron, amelynek mind a négy kvantumszámaazonos. | ||
=== | ===A09. Elemek elektronkonfigurációjának a „jelölése” (a Paschen-féle „szabályos” esetben) === | ||
=== | ===A10. A röntgen sugarak keletkezésének atom-fizikai magyarázata=== | ||
=== | ===A11. A LASER- betűszó jelentése=== | ||
=== | ===A12. A Laser működés mikro-fizikai alapja=== | ||
===B01. A „spin-pálya csatolás” definíciója és fizikai jelentése=== | |||
===B02. A (J) teljes impulzusmomentum kvantálási törvényei=== | |||
B02. A | ===B02. A spektroszkópiai jelölésrendszer === | ||
===B03. A hidrogén atom elektronjának az alapállapoti hullámfüggvénye=== | |||
===B04. A „populációinverzió” fogalma=== | |||
===B05. Az „optikai rezonátor” szerepe a laser mûködésében=== | |||
B05. Az „optikai rezonátor” szerepe a laser mûködésében | |||
==XLV. Fejezet== | ==XLV. Fejezet== | ||
===A01. A stabil atommagok (kvalitatív) „proton-neutron diagramja” === | |||
A01. A stabil atommagok (kvalitatív) „proton-neutron diagramja” | |||
===A02. A „kötési energia” fogalma=== | |||
===A03. A „felezési idõ” fogalma=== | |||
===A04. Az „aktivitás” fogalma és mértékegysége=== | |||
===A05. A „bomlási állandó” fogalma és mértékegysége=== | |||
===A06. Az „-bomlás” definíciója=== | |||
===A07. A „-bomlás” definíciója=== | |||
===A08. A „-bomlás” definíciója=== | |||
===A09. A „-bomlás” és az „antineutrinó”=== | |||
===A10. A „spontán maghasadás” jelensége=== | |||
===A11. Az atomreaktor működésének (nukleáris) alapja=== | |||
===A12 Az atombomba működésének (nukleáris) alapja=== | |||
===A13. A „tenyésztõ” reaktorok feladata=== | |||
===A14. Az „atommagfúzió” jelensége=== | |||
===A15 A „fúziós energiatermelés” aktuális kérdései (TOKOMAK)=== | |||
===A16 Amit az ITER-rõl tudni illik=== | |||
===B01. A pozitív töltések eloszlása az atommagban (szemléltetõ ábra)=== | |||
===B02. Egy nukleon kötési energiájának ábrázolása az „atomszám” függvényében.=== | |||
===B02. Az „-bomlás” magyarázata „alagúteffektussal” === | |||
===B03. A részecskék intenzitás eloszlása a kinetikus energia függvényében.=== | |||
===B04. A hasadási termékek tömeg szerinti százalékos eloszlásának kvalitatív diagramja=== | |||
===B05. A „hatáskeresztmetszet” fogalma=== | |||
[[ | [[Kategória:Villamosmérnök]] | ||
A lap jelenlegi, 2017. július 12., 15:22-kori változata
Ez az oldal a Fizika 2 tárgyhoz kapcsolódó elméleti kérdések-válaszok gyűjteménye! A Hudson-Nelson könyv fejezeteinek a végén található ellenőrző kérdések közül azok vannak itt, amiket az előadók megoldásra javasoltak.
Szerkesszétek és bővítsétek!
- "A" típusú kérdések: A tananyag legfontosabb, szükséges alapismereteit foglalja össze (ez jelentheti az a tudás "elégséges" szintjét).
- "B" típusú kérdések: A tananyag által megkívánt további ismereteket öleli fel mindez tulajdonképpen a tudásszintet határozza meg.
A ZH-kon és a vizsgákon lényegében ezen ismeretek számonkérése történik. A vizsga harmadik része 5 db. szöveges kifejtést igénylő kérdést tartalmaz, amelyek a ebből kérdésgyűjteményből valók.
XXIV. Fejezet
A01. A Coulomb törvény.
Két, és töltésű, egymástól távolságra lévő pontszerű test között ható erő:
ahol , a vákuum permittivitása.
A02. A vezető és szigetelő fogalma.
- Vezető anyagokban az elektromos töltések szabadon mozoghatnak.
- Szigetelő anyagokban az elektromos töltések sokkal kevésbé mozgékonyak.
- Félvezető anyagok vezetőképessége minimális szennyezőanyag hatására lényegesen megváltozik.
A03. Az elektromos térerősség definíciója és mértékegysége.
Az erőteret létrehozó töltés és a egységnyi próbatöltés közötti erőt adja meg az elektromos térerősség:
Mértékegysége:
A04. Az elektromos erővonalak definíciója.
Az elektromos erővonalak olyan elképzelt görbék, melyek segítségével szemléltetni lehet az elektromos tér szerkezetét. Tulajdonságok:
- Egy kis dV térfogatba rajzolt erővonalak sűrűsége megadja, hogy ott mekkora az _E_ térerősség-vektor nagysága.
- Az erővonalak érintője bármely pontban megadja az _E_ térerősség-vektor irányát.
- Az erővonalak pozitív töltésekből indulnak ki és negatív töltésekben végződnek.
A05. Az elektromos dipólus definíciója.
Két azonos nagyságú de ellentétes előjelű, egymástól a térben elválasztott pontszerű töltés.
A06. Homogén elektromos tér hatása az elektromos dipólusra.
Homogén elektromos térbe helyezve a dipólusra _M_ forgatónyomaték hat, annak a függvényében, hogy a pozitív és negatív töltést összekötő, a pozitív töltés felé mutató _p_ elektromos dipólmomentum-vektor és az _E_ térerősség-vektorok mekkora szöget zárnak be.
ahol a dipólust alkotó két töltés abszolút értéke, pedig a két töltés távolsága.
A forgatónyomaték-vektor ebben az esetben:
Nagysága:
B01. Elektromos dipólus terének számítása a tér speciális pontjaiban.
Közeli tér
Az _y_ tengelyen fekvő dipólus által keltett térerősség a dipólustól _x_ távolságban, az _x_ tengely irányában:
http://www-antenna.ee.titech.ac.jp/~hira/hobby/edu/em/dipole2/near.gif
Távoli tér
Ha a szorzat értéke konstans, nagy távolságokban ugyanakkora térerősséget eredményez.
http://www-antenna.ee.titech.ac.jp/~hira/hobby/edu/em/dipole2/far.gif
B02. Homogén erőtérbe helyezett elektromos dipólus (potenciális) energiája.
Potenciális energia-különbség azon állapotok között, amikor a dipólmomentum a külső erőtérrel illetve szöget zár be:
Célszerű a potenciális energia 0 szintjének azt az állapotot választani, amikor _p_ és _E_ egymásra merőlegesek.
B03. Dipólus inhomogén erőtérben.
- Inhomogén erőtérben a dipólus töltéseire ható erő nem egyenlő.
- A dipólusra nem csak forgatónyomaték hat, hanem azt az eredő erő nagyobb térerősségű helyek irányába mozgatja.
- Az elektromos erőterek indukált dipólmomentumot hozhatnak létre, ha az erőtér a töltéseloszlás kismértékű átrendeződését okozza.
- A pozitív töltések kis mértékben ez elektromos erőtér irányában (), a negatív töltések ezzel ellentétes irányban mozdulnak el.
B04. Egyenletesen töltéseloszlású, véges hosszú "vonaltöltés" tere.
Az _E_ térerősség kiszámítását úgy végezzük, hogy az egyes dq töltéselemek által a _P_ pontban létrehozott dE térerősségvonalakat összegezzük.
Egy dq töltéselem által létrehozott dE térerősség:
Az összes töltéselem által létrehozott E teljes térerősség
B05. Egyenletes töltéseloszlású gyűrű tere (a forgástengely mentén).
Hudson-Nelson 586. o. 24-10 példa Csak a végeredményt írom le, de szerintem a vizsgában le kell írni a levezetést is!
Általános esetben:
Amennyiben nagyon közel vagyunk a tárcsához, vagy, analóg módon, ha a tárcsa sugara nagyon nagy:
Amenniyben nagyon távol vagyunk a gyűrűtől, vagy, analóg módon, ha a gyűrű sugara nagyon kicsi:
A fenti egyenletekben:
- a gyűrűtől mért távolság a forgástengelyen,
- a gyűrű sugara,
- a gyűrű teljes töltése.
B06. Egyenletes felületi töltéseloszlású korong tere (a forgástengely mentén).
Hudson-Nelson 587.o 24-11 példa Csak a végeredményt írom le, de szerintem a vizsgában le kell írni a levezetést is
Általános esetben:
Amennyiben nagyon közel vagyunk a tárcsához, vagy, analóg módon, ha a tárcsa sugara nagyon nagy:
Amenniyben nagyon távol vagyunk a tárcsától, vagy, analóg módon, ha a tárcsa sugara nagyon kicsi:
A fenti egyenletekben:
- a korongtól mért távolság a forgástengelyen,
- a korong sugara,
- a korong felületi töltéssűrűsége.
B07. A térerősség meghatározása egyenletes töltéseloszlású körív centrumában.
Hudson-Nelson 587.o 24B-20 példa Csak a végeredményt írom le, de szerintem a vizsgában le kell írni a levezetést is
Általános esetben:
A fenti egyenletben:
- a körív sugara,
- a körív vonalmenti töltéssűrűsége,
- a körív nyílásszöge.
XXV. Fejezet
A01. Az elektromos fluxus (általános) definíciója.
Egységnyi felületet metsző elektromos erővonalak száma. Számítása: az elektromos tér integrálja a kérdéses felületen.
A02. Az elektrosztatika Gauss törvénye.
Az inhomogén elektromos mező fluxusa (forráserőssége) tehát az elektromos térerősségvektor zárt felületre vonatkozó felületi integrálja, és egyenesen arányos a zárt felületen belüli össztöltéssel. Ez az elektrosztatika I. alaptörvényének integrális alakja, amelyet Gauss-törvénynek és Maxwell I. törvényének is nevezzük.
A03. Ponttöltés terének a meghatározása a Gauss-törvény segítségével.
A q pontszerű töltés teljes elektromos fluxusa:
Ha egy zárt felület besejében (bárhol) _q_ töltés található, akkor a teljes felületre a integrál értéke mindig
A04. A vákuum dielektromos állandójának az SI mértékegysége.
Megjegyzés: Általában mindent egységrendszerben kérnek, emiatt írtam úgy a fentit, ahogy. De érdemes tudni, hogy a Volt nem SI alapegység! Tehát, nagyon szigorúan, csak SI alapegységekkel kifejezve:
B01. Egyenletesen töltött gömbfelület terének a meghatározása a Gauss törvény segítségével.
B02. Homogén töltéseloszlású tömör gömb elektromos terének a meghatározása a Gauss törvény segítségével
Hudson-Nelson 604.oldal 25-7 példa
B03. Végtelen hosszú egyenletes vonaltöltés terének meghatározása a Gauss törvény segítségével
Hudson-Nelson 601.oldal 25-3 példa
B04. Állandó töltéssűrűségű, végtelen hosszú henger terének a meghatározása a Gauss törvény segítségével
Hudson-Nelson 602.oldal 25-4 példa
B05. Egyenletesen töltött síkfelület terének a meghatározása a Gauss törvény segítségével
Hudson-Nelson 603.oldal 25-5 példa
B06. Tetszőleges alakú, töltött vezető elektromos terének jellegzetes tulajdonságai.
B07. Véges vastagságú, üreges, vezető gömbhéj elektrosztatikus tulajdonságai.
Hudson-Nelson 608.oldal 25-9 példa
XXVI. Fejezet
A01. Az elektromos potenciál (általános) definíciója.
A potenciál a térerősség út szerinti integrálja.
A02. Az ekvipotenciális felületek fogalma.
Az elektromos mezőt erővonalak mellett azonos potenciálú felületekkel, ún. ekvipotenciális (szint-, nívó-) felületekkel szokás szemléltetni.
A03. Az erővonalak és az ekvipotenciális felületek kapcsolata.
Az erővonalak mindig merőlegesek az ekvipotenciális felületekre.
Az erővonalaknak töltéseken kell végződniük.
A04. Az elektromos potenciál meghatározása ponttöltés esetében.
, ha
A05. A "csúcshatás" jelensége.
A csúcsokban nagyobb a töltéssűrűség, mint az enyhe görbületű helyeken. A levegő molekulái dipólusokká válnak, melyeket a töltött csúcs magához vonzza vagy eltaszítja. Az eltaszított részecskék árama elhajlítja a gyertya lángját, vagy forgásba hozza a kereket. Csúccsal ellátott testek könnyen elveszítik töltésüket.
Más leírás: A feltöltött, vagy elektromosan megosztott vezető csúcsaiban felhalmozodó töltések a csúcsokban összesűrűsödnek, erős inhomogén mezőt hoznak létre.
B01. Az elektromos potenciál meghatározása egyenletes töltéseloszlású gyűrű forgástengelye mentén.
B02. Az elektromos potenciál meghatározása egyenletes felületi töltéseloszlású korong forgástengely mentén.
B03. Az elektromos potenciál meghatározása egyenletes töltéseloszlású körív centrumában.
B04. Az elektromos potenciál meghatározása egyenletesen töltött gömbfelület terében.
B05. Az elektromos potenciál meghatározása homogén töltéseloszlású tömör gömb elektromos terében.
B06. Az elektromos potenciál meghatározása végtelen hosszú egyenletes vonaltöltés terében.
B07. Az elektromos potenciál meghatározása pontszerű dipólus esetén.
B08. Az elektromos potenciál meghatározása egyenletesen töltött síkfelület terében.
B09. Az elektromos potenciál mint a térerősség "gradiense".
B10. A "gradiens" matematikai alakja Descartes és gömbi koordinátarendszerben.
B11. A "térion-mikroszkóp" működésének fizikai alapelve.
Hudson-Nelson 630. oldal 26-16 ábra és szövege
XXVII. Fejezet
A01. A kapacitás fogalma
C=Q/U
A fémre vitt töltés és a létrejött potenciál hányadosa, amely a fémtestre jellemző állandó.
C/V=F(farad)
A02. Egyedülálló gömb kapacitása
IZOLÁLT, R SUGARÚ GÖMB KAPACITÁSA
A03. A sikkondenzátor kapacitása
a relatív permittivitás / dielektromos állandó
A04. A dielektromos állandó fogalma
C és (az eredeti kapacitás) hányadosát a dielektrikum reatív permittivitásának vagy dielektromos állandójána neevzzük és -val (kappa) jelöljük.
A05. A kondenzátor energiája
B01. A hengerkondenzátor kapacitása
B02. A gömbkondenzátor kapacitása
B03. Rétegezett dielektrikumot tartalmazó síkkondenzátor kapacitása (kétféle).
Hudson-Nelson 644.o 27-12 ábra, 27-9 példa
B04. Az elektromos erőtér energiasűrűsége.
Maxwell (IX)-ből:
XXVIII. Fejezet
A01. Az elektromos áramsűrűség(vektor) fogalma
A vezető tekintetbe vett A keresztmetszetén a kis delta t időköz alatt átáramló delta Q töltésnek és delta t-nek a hányadosát, pontosabban ennek a delta t ->0-hoz tartozó határértékét:
I= , pontosabban I= dQ/dt [I]= A (amper)
iránya: a pozitív töltések mozgásiránya
A02. Az elektromos áram fogalma
A töltések, azaz az elektromos tulajdonságú részecskék (elektronok, ionok) egyirányú, rendezett mozgása.
A03. A differenciális Ohm törvény
A04. A Joule törvény.
(egyenáram esetén)
B01. Az elektromos áramsűrűség meghatározása mikroszkopikus adatokkal.
B02. Néhány elektromos eszköz (I,V) karakterisztikája.
B03. A kritikus hőmérséklet fogalma szupravezetőknél.
XXIX. Fejezet
A01. Az egyenáramú áramkörök és a Kirchhoff törvények.
I. Huroktörvény:
II. Csomóponti törvény:
A02. A szuperpozíció elve.
Lényege: a gerjesztést válaszba vivő operátor lineáris, azaz konstansszorost konstansszorosba, összeget összegbe visz át. Ha pl. két feszforrást kötünk egy rezisztív hálózatra, akkor a megjelenő feszültség és áram értékek olyanok, mintha a forrásonként keletkező értékeket összeadnánk.
A03. A feszültségmérő műszerek belső ellenállása.
A04. Az árammérő műszerek belső ellenállása.
B01. A Wheatstone -híd
B02. Feszültségmérés kompenzációs módszerrel.
B03. Feszültségforrások belső ellenállása és kapocsfeszültsége.
B04. Az I(t) függvény kondenzátorok feltöltése (egy R és C) esetén .
Részletesen: ld. Jelek és Rendszerek 1 :)
B05. Az I(t) függvény kondenzátorok kisütése (egy R és C) esetén.
B06. Energiaviszonyok kondenzátor feltöltésekor (29-12 példa).
B07. Találjuk ki a 29-11 feladathoz tartozó 29-18a ábrát!
XXX. Fejezet
A01. Mágneses térben mozgó ponttöltésre ható (Lorentz) erő.
A02. Homogén mágneses térben síkmozgást végző ponttöltés kinematikai jellemzői.
Mivel a Lorentz-erő mindig merőleges a sebességvektorra, így a mágneses mező erővonalainak síkjában körmozgás alakul ki, méghozzá összefüggésnek megfelelően.
A03. A sebességszűrő (-szelektor) működési elve.
Mivel a Lorentz-erő sebességtől függ, így más eltérítő erő hat a mágneses térbe kerülő részecskékre, így más-más parabola pályán fognak mozogni.
A04. Mágneses térben lévő áramjárta vezetőre ható erő.
A05. A mágneses dipólus fogalma.
A06. A mágneses fluxus fogalma
B01. A ciklotron működési elve.
B02. A mágneses dipólusra ható forgatónyomaték.
B03. Mágneses térben lévő mágneses dipólus (potenciális) energiája.
B04. A galvanométer működési elve.
B05. A Hall effektus jelensége.
B06. A lineáris "tömegspektrométer" működési elve.
XXXI. Fejezet
A01. A Biot-Savart törvény
A02. Az Ampere- törvény
- Árammal átjárt vezető (egy db) közelében:
- Tetszőleges áramokra, vákuumban, ahol A a zárt görbére feszített felület:
A03. A mágnese tér számítása (igen hosszú) szolenoid belsejében
Levezetés: A fenti Ampere-tv. baloldalának integráljához egy olyan téglalapot veszünk, amelynek egyik oldala a tekercs belsejében halad, vele párhuzamosan "igen messze" a szemközti oldal, és a tekercs tengelyére merőlegesen fut a harmadik és negyedik oldal. Így a baloldal közelítő értéke , ugyan három oldalon elhanyagolható a értéke. A jobb oldalhoz a felület az előbbi görbére, a téglalapra illeszkedik, azaz az áram n-szer döfi át merőlegesen ezt a felületet, tehát a felületi integrál értéke , vagyis , azaz a B indukció értéke: (iránya: csukott tenyeres jobbkézszabály)
B01. Végtelen hosszú, egyenes áramjárta vezető mágneses terének számítása Biot-Savart törvénnyel.
Igen hosszú levezetés:
B02. Két párhuzamos (egyenes) vezető között ható erő.
ld: http://en.wikipedia.org/wiki/Amp%C3%A8re%27s_force_law
B03. Végtelen hosszú, egyenes áramjárta vezető mágneses terének számítása az Ampere törvény segítségével.
Levezetés: A körintegrálhoz tartozó görbe egy r sugarú kör, aminek a középpontjában a vezető van, és a kör síkja merőleges a vezetőre, így hasonlóan A03-hoz és B04-hez, a vezetőtől r távolságban a B indukció értéke: (iránya: csukott tenyeres jobbkézszabály)
B04. Toroid mágneses terének a számítása.
toroid: fánk alak :) Levezetés: a toroid belsejében felveszünk egy kört, így A03-hoz hasonlóan , az erre illeszkerdő felületen pedig n-szer halad át az áram, így , azaz a B indukció értéke: (iránya: csukott tenyeres jobbkézszabály)
B05. A vákuum mágneses permeabilitása (az SI mértékegység rendszer)
XXXII. Fejezet
A01. A mágneses fluxus definíciója és mértékegysége.
Egységnyi felületet metsző mágneses erővonalak száma. Számítása: a mágneses tér integrálja a kérdéses felületen.
A02. A Faraday-féle indukció törvény mágneses térben álló vezető hurok esetén ("Nyugalmi indukció")
Egy áramkörben indukált feszültség az áramhurok által határolt felületen átmenő mágneses fluxus egységnyi idő alatti megváltozásával egyenlő. Egy menet esetén: N menet esetén:
A03. A mozgási indukció
Ha a fluxus megváltozása a vezető és a mágnes egymáshoz viszonyított mozgásából ered, akkor mozgási indukcióról beszélünk. Homogén mágneses térben (az indukció vonalakra merőlegesen) mozgó rúd esetén:
A04. A Faraday-féle indukció törvény általános (nyugalmi+mozgási) esetben.
A05. A Faraday-féle indukció törvény (vezetõ hurok nélküli) legáltalánosabb alakja.
A06. A Lenz törvény
Zárt hurokban olyan irányú áram indukálódik, hogy mágneses erőtere az áramot létrehozó fluxusváltozást csökkentse.
A07. Az önindukciós együttható (induktivitás) definíciója és mértékegysége.
Egy tekercsben az áram kialakulását fékező önindukciós feszültséggel arányos tényező a tekercs induktivitása (L).
A08. Szolenoid önindukciós együtthatója.
A10. Az áramerõsség idõbeli változása tekercs ki-, bekapcsolása esetén.
A11. A mágneses tér energiasûrûsége (Egységnyi térfogatra jutó energia)
B01. A kölcsönös induktivitás fogalma és mértékegysége.
Két tekercs "elég közel" van egymáshoz, akkor ha az egyik tekercsben megváltozik az áramerősség, az a másik tekercsben feszültséget indukál, ennek nagysága: az 1-es tekercs a 2-esre vonatkozó kölcsönös induktivitása. Mértékegysége ugyanúgy henry.
B02. Az örvényáram
Ha egy tömör vezető anyag mágneses térben mozog, akkor az indukált áramok a vezető tömb belsejében, annak teljes térfogatában cirkulálnak.
B03. A soros RL áramkör alapegyenlete(i).
Bekapcs:
Kikapcs:
B04. Tekercsben tárolt (mágneses) energia
XXXIII. Fejezet
A01. Kis köráram (mágneses dipólus) mágneses terének (B) erõvonal szerkezete.
A dipólustól távol nagyon hasonlít az elektromos dipólus szerkezetéhez, a dipólus középpontjában és környezetében azonban ellentétes irányú azzal. http://img252.imageshack.us/img252/1142/koraramsx8.jpg
A02. Inhomogén mágneses térbe helyezett paramágneses anyagra ható erő.
Vonzó. Az atommag körül keringő elektronok elemi köráramokként foghatók fel, ami mágneses dipólustérrel együtt jár. Ezek az elemi mágneses momentumok paramágneses anyagokban nem semlegesítik egymást. Külső mágneses erőtér hatására az erőtér irányába rendeződnek, így eredő mágneses dipólmomentum alakul ki. Korábbi tanulmányainkból tudjuk, hogy mágneses dipólmomentumra olyan eredő erő hat, amely a nagyobb térerősség tartomány felé húzza.
A03. Inhomogén mágneses térbe helyezett diamágneses anyagra ható erő.
Taszító. Az elemi mágneses dipólmomentumok diamágneses anyagokban semlegesítik egymást, külső inhomogén mágneses erőtér hatására az elemi köráramok pályasugara változatlan marad, azonban a keringő elektronok sebessége megváltozik. Az egyik esetben a sebessége nő, emiatt B-vel ellentétes irányú, nagyobb mágneses momentuma lesz, a másik esetben kisebb, a B-vel egyező irányú mágneses momentum alakul ki. Mindkét effektus B fluxussűrűségű külső mágneses erőtérrel ellentétes irányú eredő dipólusmomentum kialakulásához vezet. Tehát a diamágneses anyagokra inhomogén erőtérben a csökkenő erőtér irányába mutató erő hat.
A04. A ferromágneses anyagok mágneseződése
A ferromágneses anyagokat mágneses domének alkotják. Egy doménen belüli összes atom mágneses orientációja azonos irányú. Ezen domének default állapotban (mágneses orientációjukat tekintve) rendezetlenül helyezkednek el, így az eredő mágneses momentum zérus. Külső mágneses tér hatására azonban az erőtérrel egyező irányú domének nőni kezdenek, más orientációjú domének "átrendeződnek" az erőtér irányába, így a doménfalak eltolódnak. Az erőtér megszűnésével a mágneses momentum nagy része megmarad. Így mágnesezett lett az anyag.
A05. A mágneses térerősség („H” vektor) fogalma és mértékegysége.
A mágneses térerősségnek nevezzük azt a fizikai mennyiséget, amellyel az elektromos áram által létrehozott mágneses erőteret jellemezzük. mértékegysége: amper/méter
A06. A mágneses permeabilitás és mértékegysége.
B01. A paramágnesség mikrofizikai magyarázata.
ld. A2
B02. A diamágnesség mikrofizikai magyarázata
ld. A3
B02. A ferromágnesesség mikrofizikai magyarázata
ld. A4
B03. A Curie hõmérséklet fogalma
Amely felett a hőmozgás energiája elegendő ahhoz, hogy a doménrendszert megszüntesse.
B04. A mágneses hiszterézis
A mágneses és elektromos hiszterézis jellemzően ferromágneses anyagokban lép fel, a dipólusok beállásának késlekedése, illetve akadályoztatása miatt. A visszaállás a külső erőtér nélküli állapotnak megfelelő rendezetlen helyzetbe a térerősség csökkenésekor nem a beállással azonos mértékben történik.
XXXIV. Fejezet
KIMARAD
XXXV. Fejezet
A01. Az eltolási áram definíciója
A02. Az Ampere-Maxwell egyenlet
A03. A négy Maxwell egyenlet (mint az elektrodinamika axiómarendszere)
| Megnevezés | Sorszám | Differenciális alak | Integrális alak |
|---|---|---|---|
| Gauss-törvény | I. | ||
| Faraday-Lenz-törvény | II. | ||
| Gauss mágneses törvénye |
III. | ||
| Ampère-törvény |
IV. |
A04. Az elektromágneses hullámok hullámegyenlete
A05.Az elektromágneses síkhullám (E,B) szerkezete
- A hullámfrontok a terjedés irányára merőleges síkfelületek
- Az E és B vektorok egymásra merőlegesek.
- Az E és B vektorok azonos fázisú, haladási irányra merőleges transzverzális hullámmozgást reprezentálnak.
A06. A vákuumbeli fénysebesség és az kapcsolata
A07. A Poynting-vektor definíciója és fizikai tartalma
A08. Az elektromágneses hullám energiája és impulzusa közötti kapcsolat.
U = cp
B01. Homogén, idõben változó elektromos mezõben fellépõ mágneses tér
Jó, de mi a kérdés? Hogy milyen ez a mágneses tér? Ezt írja le a megfelelő Maxwell egyenlet, amit már egyszer kérdeztél.
B02. Gyorsuló töltés által keltett elektromágneses hullámok kvalitatív magyarázata
Az elektromágneses hullámok keltésének számos módja van. Mindegy azon alapul, hogy gyorsuló töltések elektromágneses sugárzást bocsájtanak ki. A 35-12 ábra szemlélteti a sugárzás eredetét. A 35-l2a ábrán, a töltés eredetileg az O pontban nyugalomban van, az erővonalstruktúra gömbszimnesrikus. A t = 0 időpontban rövid dt ideig gyorsul és az 0’ pontba érve v = 0,2 c sebességet ér el, majd attól fogva állandó sebességgel halad és a t időpontban eléri a P pontot. Ekkor az erővonalak „összenyomódnak” (3- 12b ábra). Van tehát egy belső, „összenyomódott” térerősségstruktúra, és egy külső, eredeti, gömbszimmetrikus térerősségeloszlás, ahová még a gyorsuló, majd egyenletes sebességű mozgás hatása nem ért el. E két tartomány közötti törésvonal c sebességgel mozog kifelé, ez az a tartomány, amely a gyorsulásra vonatkozó információt őrzi. Tehát, O körül ct-nél nagyobb távolságokra, a gyorsulásra vonatkozó információ még nem érkezett meg, és a térerősségvonalak O felé, mint centrum felé mutatnak. O’-től ct-nél kisebb távolgokban az erővonalak a töltés pillanatnyi P helye felé mutatnak (35-l2b ábra). A két tartományt elválasztó törésvonalnak (rétegnek) fontos tulajdonsága, hogy ott az elektromos térerősségnek transzverzális komponense van. Ez a szétterjedő hullámban megjelenő transzverzális E térerősségű elektromos erőtér eredete.
B02. Az elektromágneses hullámok impulzusának fizikai magyarázata
Elektromágneses hullámnak kitett vezető lemezben lévő elektron v driftsebességgel kezd mozogni (azaz, mintha egy viszkózus kozegben lenne). Így F = vb az elektronra ható erő (b a "surlódási állandó"), melyet az elektromos tér fejt ki: F = Ee (e az elektron (elemi) töltése). -->
De a szerencsétlen elektronra Lorentz erő is hat:
Rakjuk be azt, amit be kell rakni: :D
Betáplált EM teljesítmény:
Jéééééé, ez majdnem ugyan az mint ott fenn a F_l nél! Dejó:
Diffegyenletet megoldva:
Tehát a W energiájú hullám által szállított impluzus: W/c
B03. A sugárnyomás fogalma és fellépésének kvalitatív magyarázata.
Azt az előző pontban láttuk, hogy az elektromágneses hullám erőt fejt ki a felületre. Az egységnyi felületre ható erőt hívjuk sugárnyomásnak (fénynyomásnak).
XXXVI. Fejezet
A01. A hullámfront és a fénysugár fogalma
A fény terjedését sugarak és hullámfrontok jellemzik, a sugarak képzeletbeli vonalak a fény terjedés mentén, a hullámfrontok pedig képzelt felületek, amelyek merőlegesek a sugarakra, a fény terjedési irányába haladnak. A hullámfront minden pontjának fázisa azonos.
A02. A Huygens-elv
A hullámfrontok minden pontja elemi (gömb) hullámok kiindulópontjának tekinthető, az elemi hullám a fény sebességével terjed tova. Egy későbbi t időpontban a hullámfront új helyzetét az elemi hullámok burkolója adja meg.
A03. A Fermat-elv
Két pont között a fény olyan úton terjed, amely megtételéhez ugyanannyi vagy kevesebb idő szükséges, mint bármely más út esetén.
A04. Tükrök leképzési törvénye
nagyítás:
A05. Homorú tükör képalkotásának sugármenete
A06. Domború tükör képalkotásának sugármenete
XXXVII. Fejezet
A01. A törésmutató fogalma
törésmutató: n
A02. A diszperzió fogalma
A törésmutató hullámhossztól való függését diszperziónak nevezzük.
A03. A Snellius-Descartes törvény
A04. A teljes fényvisszaverõdés határszöge
könnyen megkapható, ha a Snellius-Descartes törvénybe helyére -t helyettesítünk:
A05. Vékony lencsék leképzési törvénye
A06. Képalkotás gyûjtõ lencsével
Ha a tárgy távolsága a lencsétől nagyobb, mint a fókusztávolság, akkor fordított állású, valódi kép jön létre Ha a tárgy távolsága a lencsétől kisebb, mint a fókusztávolság, akkor azonos állású, virtuális kép jön létre
A07. Képalkotás szóró lencsével
Szóró lencsével mindig csak virtuális képet hozhatun létre.
A08. A Fresnel lencsék
Az úgynevezett Fresnel-lencse egy speciális kialakítású gyűjtőlencse. Jellemzője, hogy a koncentrikusan elhelyezkedő lencsemetszetek gyújtótávolságai a lencse fénytani középpontjától azonos távolságra vannak. Tömege és vastagsága a vele egyenértékű (azonos gyújtótávolságú és átmérőjű) gyűjtőlencsénél lényegesen kisebb lehet. Augustin Jean Fresnel francia fizikus eredetileg világítotornyok számára fejlesztette ki. http://www.freeweb.hu/hmika/Lexikon/Kepek/FresnLen.gif
A09. Lencsehibák
Minden konkrét lencse mutat valamilyen lencsehibát, törvénytől való eltérést, aberrációt a képalkotásban. Pl szférikus aberráció:
http://titan.physx.u-szeged.hu/~fureszg/mtech/I-02/to-26-45.jpg
B01. A fehér fény diszperziója prizmán, sugármenet.
B02. A szivárvány kialakulása
A szivárvány olyan optikai jelenség, melyet az eső vagy páracseppek okoznak, mikor a fény prizmaszerűen megtörik rajtuk, és spektrumára bomlik. http://upload.wikimedia.org/wikipedia/commons/0/03/Rainbow1.png
B02. Az üvegszál fényvezetésének kvalitatív magyarázata
B03. Vékony lencsék fókusztávolsága
XXXVIII. Fejezet
A01. A minimum helyek meghatározása két réses interferencia esetén.
kis szögek esetén:
A02. A maximum helyek meghatározása két réses interferencia esetén.
kis szögek esetén:
A03. A fáziskülönbség kialakulása fénytörõ közeg jelenléte esetén
közeg törésmutatója: n, vastagsága: b
A04. Vékony rétegrõl visszaverõdõ fény interferenciája
Amikor nagyobb törésmutatójú anyagról verődik vissza a fény, fázisugrást szenved, ha kisebbről, akkor nem. Ami lényeges: a vékony réteg első és hátsó felületéről visszaverődő fénysugarak egymással interferálnak. Higy erősítés vagy gyangítés lép fel, az a vékony réteg vastagságától függ. Ilyen jelenség játszódik le pl amikor vékony olajfolt úszik a vizen, azért látjuk olyan érdekes színűnek. Gyakorlati alkalmazása: antireflexiós réteg: a vékony réteg vastagságát pont úgy választjuk meg, hogy teljes kioltás jöjjön létre az első és hátsó felületről visszaverődött fénysugarak között:
A05. A Michelson-féle interferometer
B01. Intenzitás eloszlás két rés esetén
B02. Intenzitás eloszlás kvalitatív megadása többréses interferencia esetén
B02. A Newton gyűrűk
A Newton gyűrűk a konvex lencse és a sima üveglap közötti visszaverődések következtében keletkeznek.
XXXIX. Fejezet
A01. A Fresnel-féle diffrakció definíciója
A Fresnel-féle diffrakcióról akkor beszélünk, ha a fényforrás és az ernyő véges távolságban van az elhajlást okozó nyílástól vagy akadálytól.
A02. A Fraunhofer-féle diffrakció definíciója
Fraunhofer-féle diffrakcióról akkor beszélünk, amikor a fényforrás és az ernyő távolsága az elhajlást okozó nyílástól vagy akadálytól végtelen távolságúnak tekinthető, így a fénysugarak gyakorlatilag párhuzamosnak tekinthetőek.
A03. Az egyréses Fraunhofer-elhajlás minimumhelyei
A04. A fázisvektor (fazor) fogalma
A05. Egyetlen rés (Fraunhofer) diffrakciójának intenzitás görbéje (rajz).
A06. A felbontóképesség Rayleigh-féle kritériuma.
Két azonos intenzitású pontforrás megkülönböztetéséhez arra van szükség, hogy a egyik elhajlási képének középső csúcsa a másik elhajlási képében a maximális értékhez ne essen közelebb az első minimumnál.
A07. Többréses interferencia fõmaximumainak meghatározása.
A08. A diszperzió definíciója
A diszperzió a rácsok vagy prizmák azon tulajdonságát méri, hogy a hullámhossztartományt milyen széles szögtartományra szórja szét:
A09. A felbontóképesség definíciója.
Megmutatja, hogy a rács mennyire közeli hullámhosszúságú színeket tud szétválasztani.
A10. A Bragg-féle szórási feltétel
m = 1,2,3... = beeső sugár iránya az atomsíkhoz képest d = atomsíkok távolsága
A11. A rácssík fogalma
A12. A hologram készítésének alapvetõ (vázlatos) elrendezése.
TK 952. oldal 39-36 ábra
A13. A holografikus kép keletkezésének alapvetõ (vázlatos) elrendezése.
TK 952. oldal 39-36 ábra
B01. A Fresnel zónák fogalma
párhuzamos fénnyaláb köralakú lyukon áthaladva diffrakciós képet hoz létre egy ernyőn. Osszuk ezt a képet koncentrikus köralakú zónákra a következő képpen: A középső zonába olyan elemi hullámok érkeznek, melyek fáziskülönbsége 0 és közé esik, a következő zónába és közé esők, stb... Ezek a Fresnel-zónák
B02. Az elektromos térerõsség amplitudó (grafikus) meghatározása fazor-összeadás segítségével (ábra).
Tk. 950. oldal, 39-30 ábra
B02. Egyetlen rés Fraunhofer diffrakciójának intenzitás eloszlása (formula).
B03. Köralakú apertura felbontóképessége (minimális felbontási szög meghatározása).
B04. Rács diszperziója
B05. Rács felbontóképessége
ahol N a rések száma
B06. A Fresnel-féle zónalemez
Ha egy átlátszó filmen minden második Fresnel-zónát (ld. B01) átlátszatlanná teszünk, akkor Fresnel zónalemezhez jutunk.
XL. Fejezet
A01. A lineárisan polarizált fény
A transzverzális hullámok lineárisan polarizáltak, ha a hullámmal kapcsolatos rezgések egy, a térben rögzített iránnyal párhuzamosan mennek végbe.
A02. A dipólantennából érkező sugárzás polarizációja
Az antennából kibocsátott mikrohullámok abban az irányban vannak polarizálva, amelyben, az antenna huzalában a töltések gyorsulnak.
A03. A polarizálatlan fény
Az atomok egymástól függetlenül bocsájtják ki a fényt, az eredő fény sok hullámvonulat szuperpozíciója, amelyben a hullámvonulatok elektromos térerősség vektorainak iránya véletlenszerű eloszlást mutat a terjedés irányára merőleges valamennyi irányban.
A04. A polárszűrő
Ideális esetben a beeső polarizálatlan fény 50%át elnyeli 50%át átengedi.
A05. Malus törvénye
A06. Brewster törvénye (magyarázó ábrával)
dielektrikum határán visszaverődő fény 100%os polarizáltságának feltétele: jelölje a beesési szöget (Brewster szög).
A07. A fázistoló lemez működési elve.
A fény a polarizációjától függően két különböző terjedési sebességgel halad át az anyagokon. Tegyük fel, hogy a kalcitból vékony hasábot vágunk ki úgy, hogy adott hullámhossz esetén a hasábból kilépő o- sugár éppen fél hullámhosszal maradjon le az e sugár mögött. A két sugár fáziskülönbsége ilyenkor pont 180 fok az ilyen hasábot lambda/2es lemeznek nevezzük. lambda/4-es lemez ugyanez, csak 90 fokos fáziskülönbséget hoz létre a két sugár között.
A08. Az optikai aktivitás fogalma
Az olyan anyagokat, amelyekben a fény áthaladásakor a fény polarizációjának iránya elfordul, optikailag aktív anyagoknak nevezzük.
A09. A folyadékkristály kijelzők (LCD) működési elve
TK 971. oldal 40-18 as ábra
A folyadékkristály molekulái rendezettebbek, mint a folyadékoké, de nem annyira, mint a kristályoké. Egyes a fény polarizációs síkját elforgatják, de ezt a tulajdonságukat kis elektromos térerősség hatására elveszítik. A 90 fokos elforgatást okozó folyadékkristály lemezt két keresztezett polarizátor közé helyezik, és egy tükröt helyeznek az így kialakult rendszer mögé. Ha szemből fény éri az eszközt, akkor a 90 fokos forgatás miatt mindkét polarizátorol áthalad a fény és visszaverődve a tükörről világosnak látszik. Ha feszültséget kapcsolunk a folyadékkristály lemezre, akkor már nem forgat 90 fokkal, így a belső polarizátor kiszűr minden fényt, sötét lesz. LCD cuccokban sok millió ilyen kicsi rendszer alkot hálózatot, külön külön állítható feszültségszinttel.
B01. A Malus törvény kísérleti igazolása polárszűrő lemezekkel.
B02. A polarizálatlan fény szóródása molekulákon (magyarázó ábra)
B02. A kettőstörés sugármenete és polarizációs állapotai („o” és „e” sugarak)
B03. A lambda62-es fázistoló lemez és a fény polarizációs állapotai
B04. A lambda/4-es fázistoló lemez és a fény polarizációs állapotai
B05. A feszültség optikai vizsgálatok elve
XLII. Fejezet
A01. Rajzolja fel, a fekete test spektrális energiasűrűségét megadó ábrát.
1021 oldal 42-2 ábra.
A02. Adja meg a Stefan-Boltzmann féle törvényt
Ahol R az emittancia, vagyis a fekete test által egységnyi idő alatt egységnyi felületen, valamennyi hullámhosszán kisugárzott energia. T abszolút hőmérséklet. = Stefan-Boltzmann állandó.
A03. Mit nevezünk „ultraibolya” katasztrófának
A Rayleigh-Jeans sugárzási törvény: jól illeszkedik nagyon nagy hullámhosszon végzett mérésekhez. Másutt mindenütt drasztikus eltérés mutatkozik a mérési eredményekhez képest. Ez az eltérés a rövidhullámhosszoknál volt a legjelentősebb, ezért nevezik ultraibolya katasztrófának.
A04. Adja meg a harmonikus oszcillátor Planck-féle (energia)kvantálási törvényét
ahol h a Planck állandó
A05. Ismertesse a fényelektromos jelenséget (csak a kísérletet és annak eredményét!)
Fény hatására elektronok lépnek ki az elektródából. A kísérlet: 42-7es ábra, 1028. oldal eredménye: a kilépő elektronok kinetikus energiája nem függ a fény intenzitásától, csak a fény frekvenciájától. Van egy küszöbfrekvencia, ami alatt nem jelenik meg fotoelektron. Nem figyeltek meg késési időt abban az esetben, ha gyengébb fénnyel világítottak, ahhoz képest, amikor erősebbel.
A06. Ismertesse a fényelektromos jelenség Einstein-féle magyarázatát
Az f frekvenciájú sugárzás emissziója és abszorpciója mindig kvantumok (fotonok) formájában történik, amelyek energiája E=h*f. a foton a térben lokalizált és a forrástól c sebességgel távolodik. az anyagból akkor tud kilépni elektron ha legyőzi a kilépési munkát a fenn maradó rész pedig mozgási energia lesz -> h*f = Kmax + Wo
A07. Vázolja fel egy fotocella szerkezeti felépítését
A08. Ismertesse a Compton effektust
Vékony szénlapra monokromatikus röntgensugár nyalábot irányított és megfigyelte, hogy a lapról különböző szögben szórt röntgen sugarak ’ hullámhossza nagyobb, mint a beeső sugarak hullámhossza. A hullámhossz eltolódás végül a céltárgy anyagától függetlennek bizonyult, tehát a jelenség az elektronnal kapcsolatos. A folyamatban a foton kezdetben nyugalomban lévő elektronnal részecskeszerűen ütközik, így szórt foton és szórt elektron keletkezik. Ebből az következik, hogy a fotonnak impulzusa van, és a folyamat kísérlet során teljesült az impulzusmegmaradás törvénye:
A09. Vázolja fel az (optikai) „két réses kísérletet”
42-15 ábra.
A10. Adja meg a kétréses kísérlet „fotonos” tárgyalását
Ha mind a két rés nyitva van, akkor rendes kétréses interferencia képet látunk, azonban ha az expozíciós idő felére az egyik majd a másik rést tartjuk zárva akkor, a kép két egyréses elhajlás szuperpozíciója lesz. Ebből arra a következtetésre jutottak, hogy minden foton csak saját magával interferál.
B01. Adja meg a „feketetest” fogalmát
B02. Adja meg a Wien-féle eltolódási törvényt
Az abszolút hőmérséklet emelkedésével a spektrális eloszlás maximumához tartozó hullámhossz a rövidebb hullámok felé tolódik el. lambdam*T=állandó
B02. Adja meg a „Rayleigh-Jeans féle sugárzási törvényt
B03. Adja meg a Planck- féle sugárzási törvény matematikai alakját
B04. Rajzolja fel a „foto-elektromos áram – alkalmazott feszültség” mérési görbét
B05. Adja meg a Compton eltolódást (hullámhosszváltozást) megadó formulát
B06. Mit nevezünk „párkeltésnek”?
XLIII. Fejezet
A01. A Thoson-féle atommodell
Az atom tömegének nagy részét egy Ze pozitív töltésű folyadékgömb tartalmazza. Az elektronok ennek a pozitív folyadéknak a belsejébe vannak beágyazva. "mazsolás puding"
A02. A Rutherford-féle atommodell és hiányosságai
Nagy tömegű központi töltés a központi régióban, az úgynevezett atommagban koncentrálódik. Mi tartja együtt a mag töltéseit? Mi tartja távol a negatív töltésű elektronokat a pozitívtöltésű atommagtól?
A03. A Bohr-féle atommodell és posztulátumai
- Az elektron a proton körül körpályán mozog a klasszikus mechanika törvényei szerint.
- Az elektronok csak bizonyos megengedett r sugarú pályákon mozoghatnak, s ezeken nem sugároznak. Minthogy ezeken a pályákon az E energia állandó, az elektron ezeken a pályákon stacionárius állapotban van.
- A megengedett pályák azok, amelyeken az elektron mvr impulzusnyomatéka a 2pi-vel osztott Planck-állandó egész számú többszöröse
- stacionárius állapotom közti átmenetek úgy mennek végbe, hogy az elektron valahogyan átugrik egyik állapotból a másikba. Ekkor az atom elektromágneses hullámokat bocsát ki vagy nyel el. A két energia állapot energiája közti különbség egyenlő a kibocsátott sugárzás energiakvantumával.
A04. A hidrogén atom energia szintjei [eV]-ban kifejezve
A05. A (Bohr-féle) „korrespondencia elv”
Minden új elméletnek arra a klasszikus elméletre kell redukálódnia, amely megfelel a klasszikus helyzetre illő körülményekre alkalmazva.
A06. A de-Broglie féle hullámhossz definíciója
Az elektron az atommag körül állóhummálként van jelen, hullámhossza a De Brogli hullámhossz: , ahol p a részecske impulzusa.
A07. A de-Broglie féle (hidrogén) atom modell
A hidrogén atommodell Bohr modelljében keringő elektronoknak megfelelő a de-Broglie hullámok állóhullámok. Csomópontok közti távolság lambda / 2.
A08. A Davisson-Germer kísérlet és (kvalitatív) eredménye
Az elektronok fémfelületekről történő visszaverődést tanulmányozták, ahelyett hogy az elektronok tetszőeges szögben egyenletesen szóródtak volna egyes irányokba több, másokba kevesebb elektron szóródott, a kísérlet eredménye hogy a szokatlan szórásért az anyaghullámok a felelősek.
A09. Az idõtõl független Schrödinger egyenlet (egy dimenzióban)
A10. A hullámfüggvény Born-féle értelmezése
Einstein feltevése, hogy E^2 legyen arányos annak a valószínűségével, hogy az adott hely környezetében egy fotont találunk. Born kiterjesztette a hullámfüggvény értelmezésére azt feltételezte, hogy annak a valószínűsége, hogy a részecske az adott tartományban tartózkodik. P =
A11. A (1D) dobozba zárt részecske állapotfüggvényeinek grafikus ábrázolása
1060. oldal, 43-18 ábra.
A12. A (1D) dobozba zárt részecske "megtalálási valószínűség-sűrűség" függvényeinek grafikus ábrázolása
43-19 ábra
A13. (1D) Dobozba zárt részecske energiaszintjeinek a „n” kvantumszámtól
A14. Az alagút effektus jelensége
Az elektron hullámfüggvénye be tud hatolni a falba és a fal túloldalán is a zérustól különböző értéket vehet fel. Ez azt jelenti, hogy esetleg úgy találjuk, hogy az elektron egy kvantummechanikai alagúton átjutott a potenciál gáton ahova a klasszikus elmélet szerint sosem juthatott volna.
A15. A Heisenberg-féle határozatlansági összefüggés
Egy részecske helyének és impulzusának egyidejű mérésekor a határozatlanságok szorzata nagyobb vagy olyan nagyságrendű, mint a h/2*pi szám.
B01. A Rutherford-féle szórási kísérlet és eredménye
B02. A (Bohr-féle) korrespondencia elv érvényessége hidrogén atom esetén
B02. Az állapotfüggvény normálása
B03. A (1D) dobozba zárt részecske normált állapotfüggvényei
B04. Az „alagút mikroszkóp” mûködési elve
B05. A Bohr-féle „komplementaritási elv”
XLIV. Fejezet
A01. Az (idõfüggetlen) 3D Schrödinger-egyenlet Descartes koordináta rendszerben
A02. A hidrogén atom elektronállapotainak általános (szeparált) matematikai alakja
A03. A (L) perdület nagyságának a kvantálási törvénye
l a mellékkvantumszám
A04. A (L) perdület „z” irányú komponensének a kvantálási törvénye
m a mágneses kvantumszám
A05. A () perdület vektor (!) kvantálásának grafikus szemléltetése
1079. oldal 44-3 as ábra
A06. A Stern-Gerlach kísérlet
A kísérlet a spin-mégneses momentum beállását demonstrálta a mágneses térben. Semleges ezüst atomokból álló sugarat bocsátottak keresztül inhomogén mágneses téren. Az ezüst atom mágneses momentuma egyetlen vegyérték elektronból származik, amelynek kvantummechanika szerint nincs pálya-mágnesesmomentuma (l = 0), ezért a mágneses momentum csak a spinnek tulajdonítható. A kérdés az, hogy hogy a mégneses téren átlőtt atomnyaláb egy vagy három foltban csapódik az ernyőre (Bohr illetve Sommerfeld törvényei szerint). A várakozásokkal ellentétben 2 jól szétválasztható vonal érkezett, bizonyítva ezzel a spin-mágnesesmomentum térbeli orientációját a mágneses tér hatására.
A07. Az (S) elektron-spin kvantálási törvénye
A08. A Pauli-féle kizárási elv
Egy atomban nem lehet két olyan elektron, amelynek mind a négy kvantumszámaazonos.