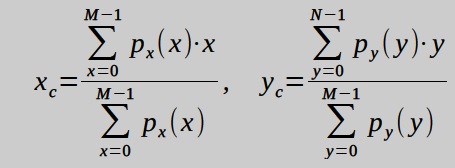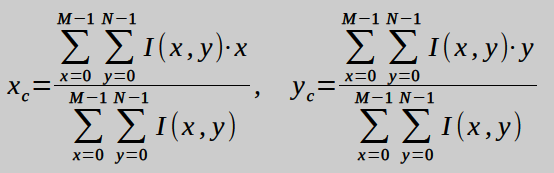„Számítógépes látórendszerek - Ellenőrző kérdések: Mérések” változatai közötti eltérés
a autoedit v2: fájlhivatkozások egységesítése, az új közvetlenül az adott fájlra mutat |
|||
| (32 közbenső módosítás, amit 4 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
{{Vissza|Számítógépes látórendszerek}} | {{Vissza|Számítógépes látórendszerek}} | ||
== Hogyan definiálhatjuk egy objektum pozícióját? Ismertesse a pozíciómérés lehetőségeit. Mutassa meg, hogy lehet a pozíció értékét meghatározni bináris és maszkolt szürkeárnyalatos képeken. == | == Hogyan definiálhatjuk egy objektum pozícióját? <br/> Ismertesse a pozíciómérés lehetőségeit.<br/> Mutassa meg, hogy lehet a pozíció értékét meghatározni bináris és maszkolt szürkeárnyalatos képeken. == | ||
Egy 2D-s képet ábrázolhatunk egy derékszögű koordinátarendszerben, ahol az egyes pixelekhez hozzárendelhetünk egy (x,y) egész koordinátapárt. A koordinátarendszer középpontja tetszőlegesen, feladattól függően megválasztható, de általában a bal felső sarokban lévő pixelhez rendeljük hozzá a (0,0)-t. | Egy 2D-s képet ábrázolhatunk egy derékszögű koordinátarendszerben, ahol az egyes pixelekhez hozzárendelhetünk egy (x,y) egész koordinátapárt. A koordinátarendszer középpontja tetszőlegesen, feladattól függően megválasztható, de általában a bal felső sarokban lévő pixelhez rendeljük hozzá a (0,0)-t. | ||
Egy objektum pozíciója az objektum egy jellegzetes koordinátapárjával jellemezhető. | Egy objektum pozíciója az objektum egy jellegzetes koordinátapárjával jellemezhető. | ||
Ez a koordinátapár lehet: | Ez a koordinátapár lehet: | ||
geometriai középpont – az objektumot befoglaló téglalap/kör középpontja | geometriai középpont – az objektumot befoglaló téglalap/kör középpontja | ||
tömegközéppont | tömegközéppont | ||
=== Tömegközéppont <math>(x_c,y_c)</math> meghatározása === | === Tömegközéppont <math>(x_c,y_c)</math> meghatározása === | ||
A kép mérete: M | A kép mérete: <math> M \cdot N </math> pixel (<math>M</math> az oszlopok száma, <math>N</math> a soroké) | ||
<math> p_x(x) = </math> az x koordinátájú | *<math> p_x(x) = </math> az <math> x</math> koordinátájú oszlopban a vizsgált objektum pixeleinek száma | ||
<math> p_y(y) = </math> az y koordinátájú | *<math> p_y(y) = </math> az <math>y</math> koordinátájú sorban a vizsgált objektum pixeleinek száma | ||
==== Bináris képekre ==== | ==== Bináris képekre ==== | ||
[[File:Számítógépes_látórendszerek_bináris_kép_1.jpg]] | |||
==== Szürkeárnyalatos képekre ==== | ==== Szürkeárnyalatos képekre ==== | ||
<math>I(x,y) </math>: intenzitásfüggvény | <math>I(x,y) </math>: intenzitásfüggvény | ||
[[File:Számítógépes_látórendszerek_szürkeárnyalatos_kép_1.png]] | |||
=== Geometriai középpont <math>(x_g,y_g)</math> meghatározása === | === Geometriai középpont <math>(x_g,y_g)</math> meghatározása === | ||
<math> | ====Meghatározás a befoglaló téglalap alapján==== | ||
<math> x_{min}, x_{max}, y_{min}, y_{max} </math> : az objektum legszélső pixeleinek koordinátái | |||
<math> x_g = \frac{x_{min} + x_{max}}{2} </math> és <math> y_g = \frac{y_{min} + y_{max}}{2} </math> | |||
<math> (x_g, y_g) </math> a téglalap középpontja, azaz a geometriai középpont. | |||
====Meghatározás a befoglaló kör alapján==== | |||
* egyértelmű, ha 3 ponton érinti a kört | |||
* kör átlójáig egyértelmű, ha 2 ponton érinti a kört. | |||
== Hogyan definiálhatjuk egy objektum orientációját? Sorolja fel az orientációmérés lehetőségeit, illetve röviden ismertesse ezek alapelvét. == | == Hogyan definiálhatjuk egy objektum orientációját? <br/>Sorolja fel az orientációmérés lehetőségeit, illetve röviden ismertesse ezek alapelvét. == | ||
Objektum orientációján egy objektum egy olyan 1D-s jellemzését értjük, mely irány-, szöginformációkat szolgáltat az adott objektumról. | Objektum orientációján egy objektum egy olyan 1D-s jellemzését értjük, mely irány-, szöginformációkat szolgáltat az adott objektumról. | ||
Objektum orientációja megadható a | Objektum orientációja megadható a | ||
| 25. sor: | 40. sor: | ||
*rá illeszthető legkisebb nyomatékú tengellyel | *rá illeszthető legkisebb nyomatékú tengellyel | ||
== Mit jelent az Euler szám? Mire használható? Adja meg a mellékelt ábra Euler számát. == | == Mit jelent az Euler szám?<br/> Mire használható?<br/> Adja meg a mellékelt ábra Euler számát. == | ||
Az Euler-szám egyike a topológiai tulajdonságoknak, melyek egy kép geometriai leírását segítik elő. Fontos része az ilyen tulajdonságoknak, hogy rubber-sheet jellegű transzormációkra invariáns. | Az Euler-szám egyike a topológiai tulajdonságoknak, melyek egy kép geometriai leírását segítik elő. Fontos része az ilyen tulajdonságoknak, hogy rubber-sheet jellegű transzormációkra invariáns. | ||
Az ilyen jellegű tulajdonságok jól használhatók formák keresésére, objektumok felismerésére, adatbázisbeli keresésre. | Az ilyen jellegű tulajdonságok jól használhatók formák keresésére, objektumok felismerésére, adatbázisbeli keresésre. | ||
Euler-szám fontos szerepet játszik például orvosi képfeldolgozásban, fertőzött sejtek felismerésében. | Euler-szám fontos szerepet játszik például orvosi képfeldolgozásban, fertőzött sejtek felismerésében. | ||
Euler-szám = (egybefüggő régiók száma) – (lyukak száma) | '''Euler-szám = (egybefüggő régiók száma) – (lyukak száma)''' | ||
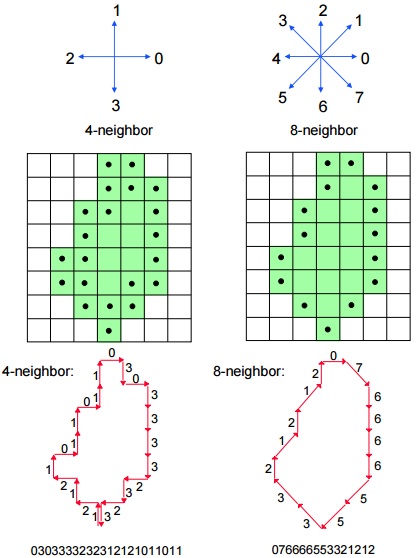
== Mit jelent a lánckód? Mire használható? Mi a különbség a 4-szomszádos és 8-szomszédos lánckód között? Mik az előnyei és a hátrányai az így ábrázolt objektumoknak? Hogyan tudunk segítségével kerület- és hossz-számítást végezni? Milyen problémák adódnak? == | [[File:Számítógépes látórendszerek Euler-szám példa.png|600px]] | ||
== Mit jelent a lánckód? Mire használható?<br/> Mi a különbség a 4-szomszádos és 8-szomszédos lánckód között? Mik az előnyei és a hátrányai az így ábrázolt objektumoknak?<br/> Hogyan tudunk segítségével kerület- és hossz-számítást végezni? Milyen problémák adódnak? == | |||
A lánckód egy veszteségmentes tömörítési algoritmus bináris képekhez. Lánckód segítségével alakfelismerést, sarokdetektálást végezhetünk. (A kódból egyértelműen látszik, hol vannak pl.: dudorok, bemélyedések.) | A lánckód egy veszteségmentes tömörítési algoritmus bináris képekhez. Lánckód segítségével alakfelismerést, sarokdetektálást végezhetünk. (A kódból egyértelműen látszik, hol vannak pl.: dudorok, bemélyedések.) | ||
Az objektum egy szélső pixelétől elindulva szomszédos, határ menti pixelekre lépkedünk. Attól függően, hogy milyen irányba lépünk tovább a pixelhez egy számot rendelünk hozzá. Ez a számsorozat alkotja a lánckódot. | Az objektum egy szélső pixelétől elindulva szomszédos, határ menti pixelekre lépkedünk. Attól függően, hogy milyen irányba lépünk tovább a pixelhez egy számot rendelünk hozzá. Ez a számsorozat alkotja a lánckódot. | ||
| 41. sor: | 58. sor: | ||
*8-szomszédos lánckód maximális hiba: 7.9% (~18-27°-os átlós egyenes) | *8-szomszédos lánckód maximális hiba: 7.9% (~18-27°-os átlós egyenes) | ||
=== Kerület = kódhossz === | |||
Hossz számításnál kerül elő az a probléma, hogy négyzetes pixelek esetén egy átlós lépés valóságos hossza sqrt(2) egység. 4-szomszédos lánckód 2 egység hosszúnak, míg a 8-szomszédos esetben 1 egység hosszúnak veszi alapból. Ha szükséges akkor ezt kompenzálni kell. | Hossz számításnál kerül elő az a probléma, hogy négyzetes pixelek esetén egy átlós lépés valóságos hossza <math>sqrt(2)</math> egység. 4-szomszédos lánckód 2 egység hosszúnak, míg a 8-szomszédos esetben 1 egység hosszúnak veszi alapból. Ha szükséges akkor ezt kompenzálni kell. | ||
[[File:Számítógépes_látórendszerek_lánckód_1.jpg]] | |||
[http://cs.haifa.ac.il/hagit/courses/ip/Lectures/Ip13_Binary.pdf Forrás] | |||
== Ismertessen szubpixeles eljárásokat. Hogyan tudunk pozíciót, kerületet, ill. területet mérni segítségükkel? == | == Ismertessen szubpixeles eljárásokat. Hogyan tudunk pozíciót, kerületet, ill. területet mérni segítségükkel? == | ||
Interpoláció alapú eljárás, mely segítségével pixel alatti pontossággal illeszthetünk görbét egy objektumra. | Interpoláció alapú eljárás, mely segítségével pixel alatti pontossággal illeszthetünk görbét egy objektumra. | ||
Megfelelő algoritmussal akár 0.1% pontosság is elérhető | Megfelelő algoritmussal akár 0.1% pontosság is elérhető. <br/><br/> | ||
''' Eljárás szürkeárnyalatos képekhez ''' | |||
#Szürkeárnyalatos képeket először is binarizáljuk. | #Szürkeárnyalatos képeket először is binarizáljuk. | ||
#Visszatérve az eredeti képhez (fekete-fehér kép alapján) az átmeneteknél lévő pixelekhez egy súlytényezőt (értéke lehet tört, megadja az interpoláció finomságát) rendelünk attól függően, hogy mennyire világos/sötét az adott pixel. | #Visszatérve az eredeti képhez (fekete-fehér kép alapján) az átmeneteknél lévő pixelekhez egy súlytényezőt (értéke lehet tört, megadja az interpoláció finomságát) rendelünk attól függően, hogy mennyire világos/sötét az adott pixel. | ||
| 53. sor: | 75. sor: | ||
Pozíciószámítás során a 3. lépésben meghatározott határpontok koordinátáit használjuk fel a képletekben. | Pozíciószámítás során a 3. lépésben meghatározott határpontok koordinátáit használjuk fel a képletekben. | ||
Kerület, területnél hasonlóan. | Kerület, területnél hasonlóan. | ||
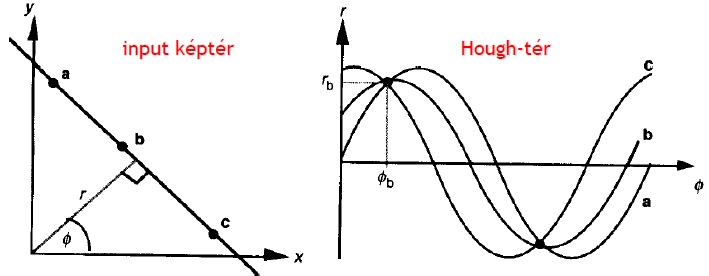
== Ismertesse az egyenesekre vonatkozó Hough-transzformáció működését. == | == Ismertesse az egyenesekre vonatkozó Hough-transzformáció működését. == | ||
=== Hough-transzformáció === | === Hough-transzformáció === | ||
A Hough-transzformáció segítségével a képen általában az | A Hough-transzformáció segítségével a képen általában az | ||
<math> f (x, y ; | <math> f (x, y ; a_1 , a_2 ,…, a_n)=0 </math> ahol | ||
<math> | <math> a_1, a_2,…, a_n </math> | ||
paraméterekkel explicit alakban megadható görbéket keressük. | paraméterekkel explicit alakban megadható görbéket keressük. | ||
A Hough-transzformáció alkalmazása célravezető, ha ismert alakú (és méretű) objektumokat keresünk a képen. | A Hough-transzformáció alkalmazása célravezető, ha ismert alakú (és méretű) objektumokat keresünk a képen. | ||
Akkor is célszerű, ha az egyenesek részben takartak vagy zajosak. | Akkor is célszerű, ha az egyenesek részben takartak vagy zajosak. | ||
=== Áttérés a Hough-térbe === | === Áttérés a Hough-térbe === | ||
Az input (kép)tér egy ( | Az input (kép)tér egy <math>(x_i,y_i)</math> pontjának az | ||
<math> r= | <math> r=x_i·\cosφ+y_i·\sinφ </math> | ||
szinuszos görbe felel meg a Hough-térben. | szinuszos görbe felel meg a Hough-térben. | ||
Az egy egyenesbe eső pontokhoz tartozó szinuszos görbék egy pontban metszik egymást. | Az egy egyenesbe eső pontokhoz tartozó szinuszos görbék egy pontban metszik egymást. | ||
=== Egyenesek meghatározása === | === Egyenesek meghatározása === | ||
| 74. sor: | 97. sor: | ||
*Az így kapott egyenes valamennyi rá szavazó ponton átmegy a képtérben. | *Az így kapott egyenes valamennyi rá szavazó ponton átmegy a képtérben. | ||
*A Hough-tér küszöbölésével megkapjuk a képtér egyeneseit. | *A Hough-tér küszöbölésével megkapjuk a képtér egyeneseit. | ||
[[File:Számítógépes_látórendszerek_egyenes_1.jpg]] | |||