„Szabályozástechnika - Folytonosidejű állapotteres szabályozók tervezése” változatai közötti eltérés
A VIK Wikiből
aNincs szerkesztési összefoglaló |
|||
| (10 közbenső módosítás, amit egy másik szerkesztő végzett, nincs mutatva) | |||
| 83. sor: | 83. sor: | ||
sdom2=conj(sdom1); | sdom2=conj(sdom1); | ||
% A zárt kör sajátértékeit tartalmazó vektor | % A zárt kör sajátértékeit tartalmazó vektor, valamint ha a rendszernek 2-nél több állapotváltozója lenne, | ||
% akkor n-2 darab, a domináns póluspárnál 3-5ször gyorsabb, valós segédpólust (scinf) is bele kellene vennünk. | |||
phic=[sdom1 sdom2]; | phic=[sdom1 sdom2]; | ||
% | % A zárt kör karakterisztikus polinomja | ||
polyphic=poly(phic); | |||
% Az irányíthatóság ellenőrzése | % Az irányíthatóság ellenőrzése | ||
| 154. sor: | 155. sor: | ||
% A megfelelő Simulink-modell megnyitása | % A megfelelő Simulink-modell megnyitása | ||
open(' | open('continuous_2'); | ||
% Most már zérus kezdeti értékekkel indítjuk a lengőrendszert és cél, hogy | % Most már zérus kezdeti értékekkel indítjuk a lengőrendszert és cél, hogy | ||
% 1 méterrel kimozdítsuk és stabilan ott tartsuk a testet. | % 1 méterrel kimozdítsuk és stabilan ott tartsuk a testet. | ||
% Várakozás billentyűlenyomásra | |||
pause | |||
</syntaxhighlight> | |||
== A beavatkozó jel kezdeti és végértékének számítása == | |||
<syntaxhighlight lang="matlab" style="font-size: 140%;"> | |||
% A feladat, hogy határozzuk meg az alapjel miatti korrekciót tartalmazó rendszer beavatkozó | |||
% jelének (u) kezdeti u(0) és végértékét u(inf), nulla kezdeti feltételek és r = k * 1(t) egységugrás alapjel esetén. | |||
r=1; % Egységugrás jellegű alapjel értéke (k = 1 választás mellett) | |||
% Kezdeti érték meghatározása: | |||
% A hatásvázlatról látszik, hogy u(t) = Nu*r(t) + K*( Nx*r(t) - x(t) ) | |||
% Ezt t=0-ra felírva: u(0) = Nu*r(0) + K*( Nx*r(0) - x(0) ) | |||
% Mivel tudjuk, hogy a szakasz 0 kezdeti feltételekkel indul így x(0)=0, tehát | |||
% u(0) = Nu*r(0) + K*Nx*r(0) | |||
u0=Nu*r+K*Nx*r | |||
% Végérték meghatározása: | |||
% Állandósult állapotban a szakasz bemenetére konstans beavatkozó jel kell, hogy kerüljön. Ehhez az szükségeltetik, | |||
% hogy a visszacsatolás zérus értékű legyen, azaz a K erősítés ki és ezáltal bemenete is zérus legyen. | |||
% Ebből következik, hogy Nx*r(inf) = x(inf). Ilyenkor mivel a visszacsatolás zérus, így u(inf) = r(inf) * Nu. | |||
uinf=r*Nu | |||
% Várakozás billentyűlenyomásra | % Várakozás billentyűlenyomásra | ||
| 175. sor: | 205. sor: | ||
% xhat' = F * xhat + G * y + H *u | % xhat' = F * xhat + G * y + H *u | ||
% Ahol xhat a becsült állapotok OSZLOP-vektora, valamint dim{xhat}=dim{x}=n. | % Ahol xhat a becsült állapotok OSZLOP-vektora, valamint dim{xhat}=dim{x}=n. | ||
% Továbbá éljünk az F=A-G*C és H=B választással. | % Továbbá éljünk az F = A-G*C és H = B választással. | ||
% A becslés hibájára (xtilde = xhat - x) így az alábbi differenciálegyenlet adódik: xtilde' = F * xtilde | % A becslés hibájára (xtilde = xhat - x) így az alábbi differenciálegyenlet adódik: xtilde' = F * xtilde | ||
% Látható, hogy az F mátrix sajátértékei fogják meghatározni, hogy milyen gyorsan csengjenek le a megfigyelés | % Látható, hogy az F mátrix sajátértékei fogják meghatározni, hogy milyen gyorsan csengjenek le a megfigyelés | ||
| 194. sor: | 224. sor: | ||
soinf=-5 | soinf=-5 | ||
% A megfigyelő karakterisztikus polinomjának gyökei | % A megfigyelő karakterisztikus polinomjának gyökei - soinf megfelelő multiplicitással (n) | ||
phio=[soinf soinf] | phio=[soinf soinf] | ||
% A megfigyelő karakterisztikus polinomja | |||
polyphio=poly(phio) | |||
% A megfigyelhetőség ellenőrzése | % A megfigyelhetőség ellenőrzése | ||
| 209. sor: | 241. sor: | ||
% A megfelelő Simulink-modell megnyitása | % A megfelelő Simulink-modell megnyitása | ||
open(' | open('continuous_obs'); | ||
% Ugyanaz a felállás mint | % Ugyanaz a felállás mint a sima állapot-visszacsatolás esetén, csak most állapotmegfigyelővel. | ||
% Látható, hogy a szabályzás ugyanolyan hatékony maradt. | % Látható, hogy a szabályzás ugyanolyan hatékony maradt, hiszen a becsült állapotok értékei körülbelül | ||
% 1 másodperc után már szinte megegyeznek az állapotok valódi értékeivel. | |||
% Állapotmegfigyelőt és alapjel miatti korrekciót is tartalmazó Simulink-modell megnyitása | |||
open('continuous_3'); | |||
% Várakozás billentyűlenyomásra | % Várakozás billentyűlenyomásra | ||
| 226. sor: | 262. sor: | ||
% kompenzálhatjuk a zavarás hatását. Ezt úgy oldjuk meg, hogy a zajt egy új állapotváltozónak (xd) tekintjük. | % kompenzálhatjuk a zavarás hatását. Ezt úgy oldjuk meg, hogy a zajt egy új állapotváltozónak (xd) tekintjük. | ||
% Mivel a zaj szakaszosan hosszú ideig konstans, ezért a deriváltja 0, a bemenettől pedig független, ezért a | % Mivel a zaj szakaszosan hosszú ideig konstans, ezért a deriváltja 0, a bemenettől pedig független, ezért a | ||
% differenciálegyenlete: xd' = 0*x + xd + 0*u. Viszont a többi változó differenciálegyenletébe már beleszól | % differenciálegyenlete: xd' = 0*x + 0*xd + 0*u. Viszont a többi változó differenciálegyenletébe már beleszól | ||
% az xd zavarást modellező fiktív állapotváltozó, méghozzá a B bemeneti mátrixon keresztül: x' = A*x + B*(xd+u). | % az xd zavarást modellező fiktív állapotváltozó, méghozzá a B bemeneti mátrixon keresztül: x' = A*x + B*(xd+u). | ||
% Tehát a kibővített rendszerünk állapotegyenletei: | % Tehát a kibővített rendszerünk állapotegyenletei: | ||
| 259. sor: | 295. sor: | ||
% Megfigyelőtervezés a kibővített rendszerhez | % Megfigyelőtervezés a kibővített rendszerhez | ||
% Ugyanaz, mint az állapotmegfigyelőnél, csak most a 'tilde rendszerre | |||
Gtilde=acker(Atilde',Ctilde',phiotilde)' | Gtilde=acker(Atilde',Ctilde',phiotilde)' | ||
Ftilde=Atilde-Gtilde*Ctilde; | Ftilde=Atilde-Gtilde*Ctilde; | ||
| 279. sor: | 316. sor: | ||
% Az integráló szabályzó célja a zavarelnyomás és a paraméterbizonytalanságok kiküszöbölése. Ezt úgy érjük el, | % Az integráló szabályzó célja a zavarelnyomás és a paraméterbizonytalanságok kiküszöbölése. Ezt úgy érjük el, | ||
% hogy új állapotként felvesszük a kimenet integrálját: xI = integrál (0->t) y(tau) dtau --> xI' = y = C* | % hogy új állapotként felvesszük a kimenet integrálját: xI = integrál (0->t) y(tau) dtau --> xI' = y = C*x | ||
% Ezzel már felírhatók a kibővített rendszer állapotegyenletei: | % Ezzel már felírhatók a kibővített rendszer állapotegyenletei: | ||
% | % | ||
| 322. sor: | 359. sor: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
[[ | [[Kategória:Villamosmérnök]] | ||
A lap jelenlegi, 2014. március 13., 17:18-kori változata
Simulink modellek
- Töltsd le!
- Csomagold ki!
- Másold be a Matlab aktuális munkakönyvtárába!
A mechanikai lengőrendszer leírása
%% Állapotteres szabályozás folytonos időben
%% Mechanikai lengőrendszer leírása
% A rendszer paraméterei:
m=2; % A test tömege
k=0.75; % Rugóállandó
b=0.25; % Csillapítás
% A rendszer differenciálegyenlete:
% F = mx'' + bx' +kx
%% Állapotteres leírás mátrixokkal
% Állapotváltozók, be es kimenet:
% x_ = [x x']'
% u = F
% y = x
%
% Az állapotegyenletek:
% x' = x'
% x'' = -(k/m)x - (b/m)x' + (1/m)F
%
% Az állapotteres leírás:
% x_' = Ax_ + Bu
% y = Cx_ + Du
%
% Az állapotteres leírás mátrixai:
A = [0 1; -k/m -b/m]
B = [0; 1/m]
C = [1 0]
D = 0
sys=ss(A,B,C,D); % A rendszer összeállítása
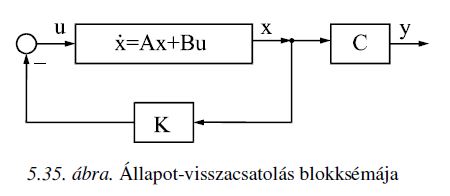
Állapotvisszacsatolás tervezése
% Az állapotteres szabályzás alapelve, hogy a zárt körben előre meghatározott pólusokat szeretnénk.
% Ezek általában egy domináns komplex konjugált póluspár (sdom1 és sdom2 - ez határozza meg a tranzienseket),
% és megfelelő számú, a domináns póluspárnál 3-5ször gyorsabb pólus (scinf).
% Ezekből a segédpólusokból n-2 darabra van szükség, ahol n az állapotváltozók száma.
% Ezt a kívánt póluselrendezést úgy érhetjük el, hogy a bemenetre egy K erősítésvektoron keresztül negatívan
% visszacsatoljuk az állapotváltozókat, azaz u = -K*x. Ha ezt behelyettesítjük a rendszer állapotegyenletébe, akkor
% x' = A*x + B*u = A*x + B*(-K*x) = (A-B*K)*x lesz a módosult rendszer állapotegyenlete. Látható hogy úgy kell
% a K értékét megválasztani, hogy az A-B*K módosult rendszermátrix sajátértékei éppen az általunk előírt
% pólusok legyenek. Az ehhez szükséges K erősítés SOR-vektor az Ackermann képlettel egyszerűen meghatározható.
damp(A) % A rendszer sajátértékei, azok csillapítása (xi)
% és csillapítatlan sajátfrekvenciája (w0)
% Gyorsabb, de jobban csillapított zárt kört szeretnénk
w0=1;
xi=0.8;
% A zárt kör általunk előírt sajátértékei
sdom1=-w0*xi+j*w0*sqrt(1-xi^2);
sdom2=conj(sdom1);
% A zárt kör sajátértékeit tartalmazó vektor, valamint ha a rendszernek 2-nél több állapotváltozója lenne,
% akkor n-2 darab, a domináns póluspárnál 3-5ször gyorsabb, valós segédpólust (scinf) is bele kellene vennünk.
phic=[sdom1 sdom2];
% A zárt kör karakterisztikus polinomja
polyphic=poly(phic);
% Az irányíthatóság ellenőrzése
Mc=ctrb(A,B); % Az irányíthatósági mátrix...
rank(Mc) % ... és rangja
% Ha rank(Mc) = n, akkor a rendszer irányítható!
% Állapotvisszacsatolás tervezése az Ackermann-képlet segítségével
K=acker(A,B,phic)
% Ellenőrizhető, hogy a zárt kör sajátértékei az általunk előírt domináns póluspár lett
damp(A-B*K)
% A megfelelő Simulink-modell megnyitása
open('continuous_1');
% A rendszerünk itt egy [-1 -0.1] kezdőértéket kap, azaz t=0-ban a lengőrendszer
% a nullpontjához képest -1 méterrel ki van mozdítva és éppen 0.1 m/s pillanatnyi
% sebességgel mozog a nullponja felé. A PLAY gombra nyomva láthatjuk, hogy a
% lengőrendszer a szabályzó segítségével beáll a nullhelyzetébe.
% Várakozás billentyűlenyomásra
pause
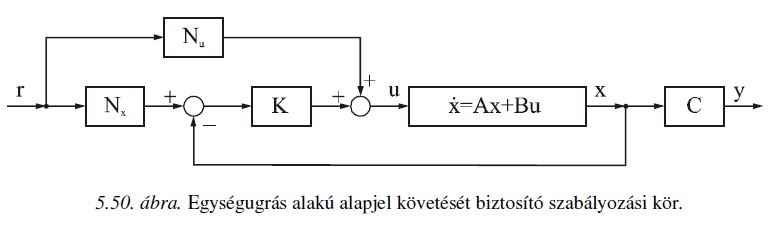
Alapjel miatti korrekció
% Amikor az állapot-visszacsatolás 0-ba (alaphelyzetbe) viszi a rendszert, a beavatkozó jel is 0 lesz,
% azaz beáll a stabilis egyensúlyi állapot. Azonban a szabályozásnak nem feltétlenül az a célja,
% hogy 0-ba irányítsunk, hanem célszerű, ha alapjelet is tud követni az eszköz. Ehhez az állapot-visszacsatolót
% "átverjük", az alábbi hatásvázlatnak megfelelően (Nx - oszlopvektor, Nu - skalár):
% Adott a szakaszunk állapotegyenletei: x' = A*x + B*u és y = C*x (legyen D=0)
% Egységugrás alapjel követése esetén célunk, hogy állandósult állapotban a kimenet 1 értékű legyen.
% Továbbá tudjuk, hogy állandósult állapotban, azaz "végtelenben" x'(inf) = 0.
% A hatásvázlatról látszik, hogy állandósult állapot esetén a K erősítő bemenetén 0 kell, hogy legyen.
% Ekkor x(inf) = Nx*r(inf) = Nx, mivel r(inf)=1 egységugrás alapjel esetén.
% Ha azonban a K bemenete 0, akkor a kimenete is 0, így u(inf) = Nu*r(inf) = Nu.
% Ezek lapján felírható az alábbi egyenletrendszer:
%
% 0 = A*x(inf) + B * u(inf) = A*Nx + B*Nu
% 1 = C*x(inf) = C*Nx
%
% Melyeket mátrixos alakban felírva:
%
% ( A B ) ( Nx ) ( 0 )
% ( C 0 ) * ( Nu ) = ( 1 )
%
% Melyből már kapásból adódik az Nx és Nu erősítések:
%
% ( Nx ) ( A B )^-1 ( 0 )
% ( Nu ) = ( C 0 ) * ( 1 )
% A keresett erősítésvektor meghatározása:
N=inv([A B; C 0])*[0;0;1];
% n darab 0-át kell az oszlopvektorba pakolni és a végére egyetlen 1-est.
% Az Nx-et és Nu-t tartalmazó vektor szétválasztása
Nx=N(1:2) % Annyi elem, ahány állapotunk van -> Nx=N(1:n)
Nu=N(end) % Skalár
% A megfelelő Simulink-modell megnyitása
open('continuous_2');
% Most már zérus kezdeti értékekkel indítjuk a lengőrendszert és cél, hogy
% 1 méterrel kimozdítsuk és stabilan ott tartsuk a testet.
% Várakozás billentyűlenyomásra
pause
A beavatkozó jel kezdeti és végértékének számítása
% A feladat, hogy határozzuk meg az alapjel miatti korrekciót tartalmazó rendszer beavatkozó
% jelének (u) kezdeti u(0) és végértékét u(inf), nulla kezdeti feltételek és r = k * 1(t) egységugrás alapjel esetén.
r=1; % Egységugrás jellegű alapjel értéke (k = 1 választás mellett)
% Kezdeti érték meghatározása:
% A hatásvázlatról látszik, hogy u(t) = Nu*r(t) + K*( Nx*r(t) - x(t) )
% Ezt t=0-ra felírva: u(0) = Nu*r(0) + K*( Nx*r(0) - x(0) )
% Mivel tudjuk, hogy a szakasz 0 kezdeti feltételekkel indul így x(0)=0, tehát
% u(0) = Nu*r(0) + K*Nx*r(0)
u0=Nu*r+K*Nx*r
% Végérték meghatározása:
% Állandósult állapotban a szakasz bemenetére konstans beavatkozó jel kell, hogy kerüljön. Ehhez az szükségeltetik,
% hogy a visszacsatolás zérus értékű legyen, azaz a K erősítés ki és ezáltal bemenete is zérus legyen.
% Ebből következik, hogy Nx*r(inf) = x(inf). Ilyenkor mivel a visszacsatolás zérus, így u(inf) = r(inf) * Nu.
uinf=r*Nu
% Várakozás billentyűlenyomásra
pause
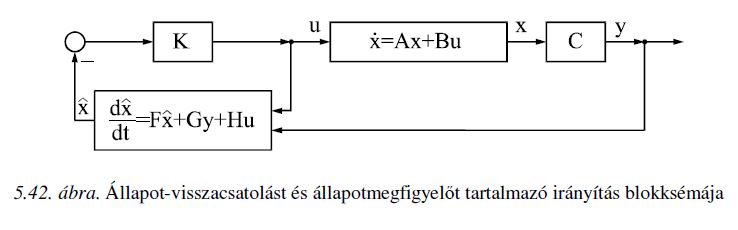
Állapotmegfigyelő tervezése
% Az állapot-visszacsatolásnál minden egyes időpillanatban szükségünk van az állapotok aktuális értékeire.
% Ez a gyakorlatban mérésekkel lenne megvalósítható, ám ez nem mindig lehetséges, vagy ha lehetséges,
% akkor csak nagyon drágán. Éppen ezért használunk állapotmegfigyelőt, ami képes minden időpillanatban
% nagyon jó közelítéssel előállítani az állapotok aktuális értékeit, a szakasz kimenetének (y) és
% bemenetének (u) ismeretében.
% A megfigyelő maga is egy lineáris folytonos idejű rendszer, melynek állapotegyenlete:
% xhat' = F * xhat + G * y + H *u
% Ahol xhat a becsült állapotok OSZLOP-vektora, valamint dim{xhat}=dim{x}=n.
% Továbbá éljünk az F = A-G*C és H = B választással.
% A becslés hibájára (xtilde = xhat - x) így az alábbi differenciálegyenlet adódik: xtilde' = F * xtilde
% Látható, hogy az F mátrix sajátértékei fogják meghatározni, hogy milyen gyorsan csengjenek le a megfigyelés
% tranziensei, azaz hogy milyen pontos legyen a megfigyelésünk. Így szeretnénk ha az F mátrix sajátértékei az
% általunk előírt gyorsaságú (a domináns póluspárnál ~5ször gyorsabb) soinf pólusok lennének.
% phio(s) = det (sI - F) = det (sI-(A-G*C)) = det (sI-(A'-C'*G')
% A fenti egyenlőség azért igaz, mivel egy rendszer és annak duálisának azonos a karakterisztikus polinomja.
% Így visszavezettük a feladatot egy fiktív rendszerhez történő állapot-visszacsatolás (K2=G') megtervezésére,
% mely fiktív rendszer rendszermátrixa A' (A transzponált), bemeneti erősítésvektora pedig C' (C transzponált).
% Ezek ismeretében az állapotmegfigyelő G vektora (vagyis annak transzponáltja) már számítható az
% Ackermann képlettel.
% A megfigyelő sajátértékei jóval gyorsabbak mint a zárt kör sajátértékei
soinf=-5
% A megfigyelő karakterisztikus polinomjának gyökei - soinf megfelelő multiplicitással (n)
phio=[soinf soinf]
% A megfigyelő karakterisztikus polinomja
polyphio=poly(phio)
% A megfigyelhetőség ellenőrzése
Mo=obsv(A,C); % A megfigyelhetőségi mátrix...
rank(Mo) % ... és rangja
% Ha rank(Mo) = n, akkor a rendszer megfigyelhető!
% Megfigyelő tervezése
% VIGYÁZAT: Itt A és C transzponáltja szerepel, továbbá az acker eredményét is transzponálni kell!
G=acker(A',C',phio)'
F=A-G*C
H=B
% A megfelelő Simulink-modell megnyitása
open('continuous_obs');
% Ugyanaz a felállás mint a sima állapot-visszacsatolás esetén, csak most állapotmegfigyelővel.
% Látható, hogy a szabályzás ugyanolyan hatékony maradt, hiszen a becsült állapotok értékei körülbelül
% 1 másodperc után már szinte megegyeznek az állapotok valódi értékeivel.
% Állapotmegfigyelőt és alapjel miatti korrekciót is tartalmazó Simulink-modell megnyitása
open('continuous_3');
% Várakozás billentyűlenyomásra
pause
Terhelésbecslő tervezése
% Tegyük fel, hogy a bemenetre rárakódik egy szakaszosan hosszú ideig konstans zaj. Az állapotmegfigyelővel
% ezt is becsülni tudjuk és ezt a becsült értéket kivonhatjuk a bemenetből (beavatkozó jelből), így
% kompenzálhatjuk a zavarás hatását. Ezt úgy oldjuk meg, hogy a zajt egy új állapotváltozónak (xd) tekintjük.
% Mivel a zaj szakaszosan hosszú ideig konstans, ezért a deriváltja 0, a bemenettől pedig független, ezért a
% differenciálegyenlete: xd' = 0*x + 0*xd + 0*u. Viszont a többi változó differenciálegyenletébe már beleszól
% az xd zavarást modellező fiktív állapotváltozó, méghozzá a B bemeneti mátrixon keresztül: x' = A*x + B*(xd+u).
% Tehát a kibővített rendszerünk állapotegyenletei:
%
% ( x' ) ( A B ) ( x ) ( B )
% ( xd' ) = ( 0 0 ) * ( xd ) + ( 0 ) * u
%
% ( x )
% y = ( C 0 ) * ( xd )
%
% Új jelöléseket bevezetve a kibővített rendszerünk állapotegyenletei:
%
% xtilde' = Atilde * xtilde + Btilde * u
% y = Ctilde * xtilde
%
% Tehát az állapotmegfigyelőnket most ehhez a kibővített "tilde" rendszerhez kell megterveznünk.
% A módosult állapotmegfigyelő differenciálegyenlete a hatásvázlatról leolvasható!
% A kibővített rendszer mátrixai:
Atilde=[A B; 0 0 0]; % n+1 nulla az utolsó sorba (SISO)
Btilde=[B;0]; % Fixen 1 darab nulla a végére (SISO)
Ctilde=[C 0]; % Fixen 1 darab nulla a végére (SISO)
% A megfigyelő sajátértékeit tartalmazó vektorban soinf most egyel nagyobb
% multiplicitással szerepel (n+1), hiszen felvettünk egy új (fiktív) állapotot
phiotilde=[soinf soinf soinf];
% Megfigyelőtervezés a kibővített rendszerhez
% Ugyanaz, mint az állapotmegfigyelőnél, csak most a 'tilde rendszerre
Gtilde=acker(Atilde',Ctilde',phiotilde)'
Ftilde=Atilde-Gtilde*Ctilde;
Htilde=Btilde;
% A megfelelő Simulink-modell megnyitása
open('continuous_4');
% t=10 secnél egy egységugrás jellegű zavarás adódik a szakasz bemenetére.
% A modellben a K,Nu és Nx paraméterek ugyanazok, mint amiket korábban meghatároztunk.
% FONTOS: A Simulink alapból 10 secundumig számol, szóval ezt az időt át kell írni 20-ra az ablak tetején!
% Várakozás billentyűlenyomásra
pause
Integráló szabályozás tervezése
% Az integráló szabályzó célja a zavarelnyomás és a paraméterbizonytalanságok kiküszöbölése. Ezt úgy érjük el,
% hogy új állapotként felvesszük a kimenet integrálját: xI = integrál (0->t) y(tau) dtau --> xI' = y = C*x
% Ezzel már felírhatók a kibővített rendszer állapotegyenletei:
%
% ( x' ) ( A 0 ) ( x ) ( B )
% ( xI' ) = ( C 0 ) * ( xI ) + ( 0 ) * u
%
% ( x )
% y = ( C 0 ) * ( xI )
%
% Új jelöléseket bevezetve a kibővített rendszerünk állapotegyenletei:
%
% xi' = Ai * xi + Bi * u
% y = Ci * xi
%
% Most ehhez a kibővített rendszerhez kell egy új Ktilde = [Kt Ki] állapot-visszacsatolást megterveznünk.
% A kibővített rendszer mátrixai:
Ai=[A zeros(2,1);C 0]; % Az első sorban n*1-es nullmátrix
% A második sorban fixen 1 darab nulla (SISO)
Bi=[B;0]; % Fixen 1 darab nulla a végére
% Az integrátor állapotának (-3)-as sajátértéket írunk elő
phictilde=[sdom1 sdom2 -3];
% Állapot-visszacsatolás számítása a kibővített rendszerre
Ktilde=acker(Ai,Bi,phictilde);
% Az állapot-visszacsatolás vektorának felbontása
Kt=Ktilde(1:2); % Annyi eleme van, ahány valódi állapotunk (n)
Ki=Ktilde(3); % Skalár
% A megfelelő Simulink-modell megnyitása
open('continuous_5');
% Vigyázat ez itt a terhelésbecslő nélküli modell továbbfejlesztése.
% Az integráló szabályozás is a bemenetre szuperponálódott zavarjelek kiküszöbölésére való.
% Itt Nu helyett egy Ki erősítés van és egy integrátor, valamint K helyett Kt !!!
% Várakozás billentyűlenyomásra
pause