„Tömegkiszolgálás - Házi feladatok 2004” változatai közötti eltérés
aNincs szerkesztési összefoglaló |
aNincs szerkesztési összefoglaló |
||
| (2 közbenső módosítás ugyanattól a felhasználótól nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
{{Vissza|Tömegkiszolgálás}} | |||
==1. feladat== | ==1. feladat== | ||
Egy részecske az origóból indulva mozog az (<i>x</i>,<i>y</i>)-síkon. Minden lépése során az _x_ és _y_ irányú elmozdulása egy-egy egymástól független, a [-1,1] intervallumon egyenletes eloszlású folytonos valószínűségi változóval írható le. Az egyes lépései függetlenek a korábbi lépésektől. Átlagosan milyen messze jut el a részecske az origótól n lépés megtétele után, ha a távolságot négyzetes középértékben számoljuk? | Egy részecske az origóból indulva mozog az (<i>x</i>,<i>y</i>)-síkon. Minden lépése során az _x_ és _y_ irányú elmozdulása egy-egy egymástól független, a [-1,1] intervallumon egyenletes eloszlású folytonos valószínűségi változóval írható le. Az egyes lépései függetlenek a korábbi lépésektől. Átlagosan milyen messze jut el a részecske az origótól n lépés megtétele után, ha a távolságot négyzetes középértékben számoljuk? | ||
| 43. sor: | 45. sor: | ||
Hogyan változnak az előbbi értékek, ha a 8 közül 4 forrás 300 csomag/perc, 4 pedig 60 csomag/perc intenzitású Poisson-folyamat szerint generál csomagokat? | Hogyan változnak az előbbi értékek, ha a 8 közül 4 forrás 300 csomag/perc, 4 pedig 60 csomag/perc intenzitású Poisson-folyamat szerint generál csomagokat? | ||
[[ | [[Kategória:Mérnök informatikus MSc]] | ||
A lap jelenlegi, 2014. március 13., 13:53-kori változata
1. feladat
Egy részecske az origóból indulva mozog az (x,y)-síkon. Minden lépése során az _x_ és _y_ irányú elmozdulása egy-egy egymástól független, a [-1,1] intervallumon egyenletes eloszlású folytonos valószínűségi változóval írható le. Az egyes lépései függetlenek a korábbi lépésektől. Átlagosan milyen messze jut el a részecske az origótól n lépés megtétele után, ha a távolságot négyzetes középértékben számoljuk?
2. feladat
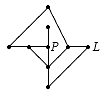
Az ábrán látható pókháló _L_ pontjába ragadt egy légy. A pók a _P_ pontból indul, és minden lépésben az aktuális pont szomszédai közül egyenletes eloszlás szerint választva halad tovább (függetlenül a korábbi választásaitól). Várhatóan hány lépésben fogja meg a pók a legyet?
3. feladat
Adott egy végtelen állapotú homogén Markov-lánc a {0,1,2,...} állapothalmazon az alábbi állapotátmeneti valószínűségekkel:
Ha a láncot az X0=0 állapotból indítjuk, mennyi lesz a valószínűség értéke?
4. feladat
Bizonyítsd be, hogy egy homogén Markov-lánc akkor és csak akkor erősen stacionárius, ha azonos eloszlású.
5. feladat
Vizsgáljunk egy _M_ forrásból és 2 kiszolgálóból álló rendszert. A források egymástól függetlenül, emlékezetmentesen generálnak igényeket, 1/2 valószínűséggel _A_ típusút, 1/2 valószínűséggel _B_ típusút (melyeket mindegyikük a saját várakozási sorában FIFO módon sorbaállít). Az _A_ típusú igényeket csak az egyik, míg a _B_ típusúakat csak a másik kiszolgáló tudja kezelni; mindkettő egy-egy igénnyel végez időegységenként.
- Stacionárius állapotban mekkora a rendszer áteresztőképessége, azaz hány igényt tud kiszolgálni időegységenként?
- M=2 forrás esetén hogyan változik a rendszer áteresztőképessége, ha a források nem egyenlő valószínűséggel generálják a kétféle igényt?
6. feladat
Tekintsük az {Sn} (n≥0) szimmetrikus bolyongást, ahol a felfelé és a lefelé lépések valószínűsége egyaránt 1/2, és S0=0. (Vagyis , ahol {Xn} független valószínűségi változók sorozata, melyek közös eloszlása P(Xn=1) = P(Xn=-1) = 1/2 ∀n≥1-re.) Legyen τ := min{n: Sn=2}, vagyis az a (minimális) lépésszám, amikor a bolyongás során először jutunk a kezdeti 0 állapotból a 2-be. Határozzuk meg a τ valószínűségi változó eloszlását generátorfüggvény segítségével!
7. feladat
Egy egyirányú úton az autók λ paraméterű Poisson-folyamat szerint érkeznek. Egy gyalogos szeretne átjutni az egyik oldalról a másikra. Mivel az út jól belátható, csak akkor indul el, amikor biztosan tudja, hogy áthaladás közben nem érkezik autó. Átlagosan mennyi ideig kell várnia a gyalogosnak a biztonságos átjutásra, ha _v_ m/s sebességgel halad és az út _x_ méter széles? Mi a valószínűsége annak, hogy nem kényszerül várakozásra?
8. feladat
Két bolha ugrál egy négyzet csúcsain, egymástól függetlenül. Az egyik mindig pozitív körüljárási irányban halad, és az ugrásai között eltelt idő λ paraméterű exponenciális eloszlású valószínűségi változó szerinti. A másik pedig mindig negatív körüljárási irányban halad μ paraméterű exponenciális eloszlású valószínűségi változó által megadott időközönként ugorva. Mi a valószínűsége annak, hogy egy t>0 időpontban a négyzet azonos csúcsán áll a két bolha? A valószínűség zárt alakban való megadásához szükséges az alábbi két hatványsor ismerete:
Értelmezés sikertelen (formai hiba): {\displaystyle \cosh x = \sum_{i=0}^\infty \frac{x^{2n}}{(2n)!}, \hspace{1em} \cos x = \sum_{i=0}^\infty (-1)^n \frac{x^{2n}}{(2n)!}. }
9. feladat
Egy távközlési társaság két város közötti digitális összeköttetés sebességét szeretné optimálisan méretezni. A felhasználók 30 hívás/perc intenzitású Poisson-folyamat szerint generálnak hívásokat, melyek hossza egymástól és a hívások között eltelt időtől teljesen független, exponenciális eloszlású 3 perc/hívás várható értékkel. Minden olyan hívást elveszettnek tekintünk, amely akkor érkezik, amikor az összeköttetés teljes kihasználtsággal üzemel ("az összes vonal foglalt"). Egy hívás 64 Kbit/sec sebességű digitális csatornát igényel. Milyen sebességű összeköttetést kell a társaságnak kiépítenie ahhoz, hogy a hívásoknak csak az 1%-a vesszen el? Hogyan változik a szükséges sebesség, ha az elveszett hívások arányát 0,1% alá akarjuk szorítani?
10. feladat
Egy 64 Kbit/sec sebességű adatátviteli csatornán szeretnénk 8 (egymástól független) igényforrás csomagjait továbbítani. Minden forrás 180 csomag/perc intenzitású Poisson-folyamat szerint generál csomagokat. A csomagok hossza exponenciális eloszlású 1024 bit/csomag várható értékkel. Határozd meg a rendszerben tartózkodó csomagok átlagos számát és egy csomag átlagos késleltetését, ha
- a források időosztás szerint használják a csatornát;
- statisztikus multiplexálást (csomagkoncentrátort) alkalmazunk.
Hogyan változnak az előbbi értékek, ha a 8 közül 4 forrás 300 csomag/perc, 4 pedig 60 csomag/perc intenzitású Poisson-folyamat szerint generál csomagokat?