„Bode-diagram kézi rajzolása” változatai közötti eltérés
A VIK Wikiből
a átláthatóbb |
aNincs szerkesztési összefoglaló |
||
| 1. sor: | 1. sor: | ||
A '''Bode-diagram kézi rajzolása''' több tantárgyból is előjöhet. Ehhez nyújt segítséget az alábbi leírás, melyet [[ZrupkoAndras|Ndroo]] készített a Keviczky-féle Szabályozástechnika-könyv | A '''Bode-diagram kézi rajzolása''' több tantárgyból is előjöhet. Ehhez nyújt segítséget az alábbi leírás, melyet [[ZrupkoAndras|Ndroo]] készített a Keviczky-féle Szabályozástechnika-könyv alapján. | ||
<div class="noautonum">__TOC__</div> | |||
==A Bode-diagram készítésének lépései== | ==A Bode-diagram készítésének lépései== | ||
=== 1. Átviteli függvény átalakítása: === | |||
#'''Átviteli függvény átalakítása:''' Ha a feladatban ehhez hasonló alak van: <math>L(s)=10\frac{s+10}{s^3+51s^s+50s}</math>, akkor át kell alakítani ilyen alakká: <math>L(s)=\frac{2(1+0,1s)}{(s(1+s)(1+0,02s))}</math>. Először a számlálót és a nevezőt is szorzattá kell alakítani, aztán annyit emelünk ki, hogy az s nélküli tagok értéke 1 legyen: <math>L(s)=10\frac{s+10}{s^3+51s^s+50s}=10\frac{s+10}{s(s+1)(s+50)}=10\frac{10}{50}\frac{1+0,1s}{s(1+s)(1+0,02s)}=\frac{2(1+0,1s)}{s(1+s)(1+0,02s)}</math>. Így minden tényező <math>1+sT</math> alakú lesz; ha eleve így adták meg, akkor ezt a lépést ki kell hagyni. | #'''Átviteli függvény átalakítása:''' Ha a feladatban ehhez hasonló alak van: <math>L(s)=10\frac{s+10}{s^3+51s^s+50s}</math>, akkor át kell alakítani ilyen alakká: <math>L(s)=\frac{2(1+0,1s)}{(s(1+s)(1+0,02s))}</math>. Először a számlálót és a nevezőt is szorzattá kell alakítani, aztán annyit emelünk ki, hogy az s nélküli tagok értéke 1 legyen: <math>L(s)=10\frac{s+10}{s^3+51s^s+50s}=10\frac{s+10}{s(s+1)(s+50)}=10\frac{10}{50}\frac{1+0,1s}{s(1+s)(1+0,02s)}=\frac{2(1+0,1s)}{s(1+s)(1+0,02s)}</math>. Így minden tényező <math>1+sT</math> alakú lesz; ha eleve így adták meg, akkor ezt a lépést ki kell hagyni. | ||
=== 2. Pólusok/zérusok felírása: === | |||
#'''Pólusok/zérusok felírása:''' Zérusok: azok a helyek ahol a számláló értéke 0 lesz, pólusok: azok a helyek, ahol a nevező értéke lesz 0. Minden szorzatalakra fel kell írni a következőt: <math>1+sT=0</math>, itt lesz a számláló/nevező értéke nulla, pl.: <math>1+0,02s=0 ~\rightarrow~ s=-50</math> az egyik pólus, a többi: <math>s=-1</math>-nél, <math>s=0</math>-nál van, a zérus: <math>s=-10</math>-nél van. | #'''Pólusok/zérusok felírása:''' Zérusok: azok a helyek ahol a számláló értéke 0 lesz, pólusok: azok a helyek, ahol a nevező értéke lesz 0. Minden szorzatalakra fel kell írni a következőt: <math>1+sT=0</math>, itt lesz a számláló/nevező értéke nulla, pl.: <math>1+0,02s=0 ~\rightarrow~ s=-50</math> az egyik pólus, a többi: <math>s=-1</math>-nél, <math>s=0</math>-nál van, a zérus: <math>s=-10</math>-nél van. | ||
=== 3. Fel/letörés: === | |||
#'''Fel/letörés:''' Ez az amplitúdó-körfrekvencia görbéhez kell (a dB-es). A pontok, ahol a görbe fel/letörik: <math>1+sT</math> alakból vagy s abszolútértéke, vagy <math>\frac{1}{T}</math> értéke (a kettő abszolútértékben ugyanaz, úgy számold ki, ahogy jól esik). A görbe feltörik, ha zéruson megy át, ilyenkor a meredeksége 20dB/dekáddal nő (a függvény meredekéségét magasabbra rajzolod), illetve letörik, ha póluson megy át, a meredeksége itt 20dB/dekáddal csökken. | #'''Fel/letörés:''' Ez az amplitúdó-körfrekvencia görbéhez kell (a dB-es). A pontok, ahol a görbe fel/letörik: <math>1+sT</math> alakból vagy s abszolútértéke, vagy <math>\frac{1}{T}</math> értéke (a kettő abszolútértékben ugyanaz, úgy számold ki, ahogy jól esik). A görbe feltörik, ha zéruson megy át, ilyenkor a meredeksége 20dB/dekáddal nő (a függvény meredekéségét magasabbra rajzolod), illetve letörik, ha póluson megy át, a meredeksége itt 20dB/dekáddal csökken. | ||
=== 4. A görbe kezdő meredeksége: === | |||
#'''A görbe kezdő meredeksége:''' ezt az integrátorokból (szimpla s szorzótagok az átviteli függvényben) nézhető meg, ha nincs ilyen: a meredekség 0, a görbe vízszintesen indul, ha egy van (egyszeres integrátor): -20dB/dekád a kezdő meredekség, ha kettő van, azaz <math>s^2</math> van (kétszeres integrátor): -40dB/dekád. A fenti példában egyszeres integrátor van, azaz -20dB/dekád a kezdő meredekség. | #'''A görbe kezdő meredeksége:''' ezt az integrátorokból (szimpla s szorzótagok az átviteli függvényben) nézhető meg, ha nincs ilyen: a meredekség 0, a görbe vízszintesen indul, ha egy van (egyszeres integrátor): -20dB/dekád a kezdő meredekség, ha kettő van, azaz <math>s^2</math> van (kétszeres integrátor): -40dB/dekád. A fenti példában egyszeres integrátor van, azaz -20dB/dekád a kezdő meredekség. | ||
=== 5. Az x tengely metszésének pontja: === | |||
#'''Az x tengely metszésének pontja:''' (vágási körfrekvencia, <math>\omega_c</math>): ezt a meredekség és az átviteli függvény szorzókonstansa (K) határozzák meg: ha a görbe meredeksége 0dB/dekád akkor nem metszi az x tengelyt (mert vízszintesen halad), ha -20dB/dekád, akkor K-nál metszi, ha -40dB/dekád, akkor <math>\sqrt{K}</math>-nál. Az egyes fel/letörések miatt úgy lehet nyomon követni, hol lesz a metszés helye, hogy megnézzük az integrátorokat/a kezdő meredekséget: ha K-ig nem változik a görbe meredeksége, akkor a meredekségnek megfelelően metszi (pl: egyszeres integrátor, K=5, ekkor -20dB/dekádos meredekséggel megy át az x tengelyen 5-nél), ha előtte megváltozik, akkor annak megfelelően (pl: kétszeres integrátor, K=16, 2-nél feltörik, ekkor 2-ig -40dB/dekád a meredekség, a tengelyt <math>\sqrt{16}</math>-nál metszené, de a feltörés miatt 2 után -20dB/dekáddal metszi az x tengelyt 16-nál.). A fenti példában K=2, egyszeres integrátor, -1-nél letörés van, ezért -40dB/dekád meredekséggel a <math>\sqrt{2}</math> pontban metszi. | #'''Az x tengely metszésének pontja:''' (vágási körfrekvencia, <math>\omega_c</math>): ezt a meredekség és az átviteli függvény szorzókonstansa (K) határozzák meg: ha a görbe meredeksége 0dB/dekád akkor nem metszi az x tengelyt (mert vízszintesen halad), ha -20dB/dekád, akkor K-nál metszi, ha -40dB/dekád, akkor <math>\sqrt{K}</math>-nál. Az egyes fel/letörések miatt úgy lehet nyomon követni, hol lesz a metszés helye, hogy megnézzük az integrátorokat/a kezdő meredekséget: ha K-ig nem változik a görbe meredeksége, akkor a meredekségnek megfelelően metszi (pl: egyszeres integrátor, K=5, ekkor -20dB/dekádos meredekséggel megy át az x tengelyen 5-nél), ha előtte megváltozik, akkor annak megfelelően (pl: kétszeres integrátor, K=16, 2-nél feltörik, ekkor 2-ig -40dB/dekád a meredekség, a tengelyt <math>\sqrt{16}</math>-nál metszené, de a feltörés miatt 2 után -20dB/dekáddal metszi az x tengelyt 16-nál.). A fenti példában K=2, egyszeres integrátor, -1-nél letörés van, ezért -40dB/dekád meredekséggel a <math>\sqrt{2}</math> pontban metszi. | ||
=== 6. Amplitúdó-körfrekvencia görbe felrajzolása: === | |||
#'''Amplitúdó-körfrekvencia görbe felrajzolása:''' ''(Lásd: könyv 88. old.)'' Itt az eddigieket kell összegyúrni eggyé, előbb bejelölöd a pontokat, ahol történik valami, majd utána rajzolod meg a görbét, az y tengelyen <math>|L(j\omega|</math>, az x tengelyen <math>\omega</math> értékével.<br/>[[Fájl:Bode-diagram_amplitudo.jpg]] | #'''Amplitúdó-körfrekvencia görbe felrajzolása:''' ''(Lásd: könyv 88. old.)'' Itt az eddigieket kell összegyúrni eggyé, előbb bejelölöd a pontokat, ahol történik valami, majd utána rajzolod meg a görbét, az y tengelyen <math>|L(j\omega|</math>, az x tengelyen <math>\omega</math> értékével.<br/>[[Fájl:Bode-diagram_amplitudo.jpg]] | ||
=== 7. Fázisgörbe értéke: === | |||
#'''Fázisgörbe értéke:''' (ez a másik görbe, a <math>\varphi</math>-s, rendes nevén: fázis-körfrekvencia görbe) a görbéhez képzeljünk el sávokat, ahol 90° a lépték az egyes értékek közt. A fenti fel/letöréseknek megfelelően változik, ha feltörik, akkor az érték nő 90°-al, ha letörik, akkor csökken 90°-al. Viszont ez nem egyik pillanatról a másikba megy végbe, hanem "átmenetszerűen", rajzban ez azt jelenti, hogy fel/letörésnél már félúton van az új állapot felé.<br/>[[Fájl:Bode-diagram fazis.jpg]] | #'''Fázisgörbe értéke:''' (ez a másik görbe, a <math>\varphi</math>-s, rendes nevén: fázis-körfrekvencia görbe) a görbéhez képzeljünk el sávokat, ahol 90° a lépték az egyes értékek közt. A fenti fel/letöréseknek megfelelően változik, ha feltörik, akkor az érték nő 90°-al, ha letörik, akkor csökken 90°-al. Viszont ez nem egyik pillanatról a másikba megy végbe, hanem "átmenetszerűen", rajzban ez azt jelenti, hogy fel/letörésnél már félúton van az új állapot felé.<br/>[[Fájl:Bode-diagram fazis.jpg]] | ||
=== 8. Fázisgörbe kezdőértéke: === | |||
#'''Fázisgörbe kezdőértéke:''' ez az integrátorok, és az átviteli függvény szorzókonstansán múlik: | #'''Fázisgörbe kezdőértéke:''' ez az integrátorok, és az átviteli függvény szorzókonstansán múlik: | ||
## a konstans ha pozitív, akkor 0° a kezdőérték, ha negatív, akkor -180° | ## a konstans ha pozitív, akkor 0° a kezdőérték, ha negatív, akkor -180° | ||
| 14. sor: | 40. sor: | ||
## ha a számlálóban volt egy szimpla s tag, akkor az 90°-al növeli. | ## ha a számlálóban volt egy szimpla s tag, akkor az 90°-al növeli. | ||
## Pl: konstans negatív, egyszeres integrátor: -180°+(-90°)=-270°, konstans pozitív, számlálóban egy szimpla s: 0°+90°=90°. A fenti példában konstans pozitív, egyszeres integrátor: 0°-90°=-90°. | ## Pl: konstans negatív, egyszeres integrátor: -180°+(-90°)=-270°, konstans pozitív, számlálóban egy szimpla s: 0°+90°=90°. A fenti példában konstans pozitív, egyszeres integrátor: 0°-90°=-90°. | ||
=== 9. Fázistöbblet meghatározása: === | |||
#'''Fázistöbblet meghatározása:''' ''(Lásd: könyv 190-191. old)'' fázistöbblet fázis-körfrekvencia görbe értékének különbsége -180°-tól a vágási körfrekvenciánál. Azaz ahol a dB-es görbe metszi az x tengelyt, ott megnézed a <math>\varphi</math>-s görbe értéke mennyire tér el a -180°-os vonaltól. Ezt a meredekség határozza meg mekkora lesz: ha -20dB/dekáddal metszi az x tengelyt: a fázistöbblet biztosan pozitív ''(Lásd: könyv 191.old, 5.35 ábra)'', ha -40dB/dekáddal metszi: a fázistöbbletet nem lehet meghatározni biztosan, olyat rajzolsz, mint az 5.36-os ábrán, ha -60dB/dekáddal metszi: a fázistöbblet biztosan negatív, ekkor a 180°-os vonal alatt megy el. A fenti példában -40dB/dekád meredekséggel a <math>\sqrt{2}</math> pontban metszi az x tengelyt a dB-es függvény, ezért a fázistöbbletet nem tudjuk meghatározni biztosan, a stabilitás határhelyzetében van. | #'''Fázistöbblet meghatározása:''' ''(Lásd: könyv 190-191. old)'' fázistöbblet fázis-körfrekvencia görbe értékének különbsége -180°-tól a vágási körfrekvenciánál. Azaz ahol a dB-es görbe metszi az x tengelyt, ott megnézed a <math>\varphi</math>-s görbe értéke mennyire tér el a -180°-os vonaltól. Ezt a meredekség határozza meg mekkora lesz: ha -20dB/dekáddal metszi az x tengelyt: a fázistöbblet biztosan pozitív ''(Lásd: könyv 191.old, 5.35 ábra)'', ha -40dB/dekáddal metszi: a fázistöbbletet nem lehet meghatározni biztosan, olyat rajzolsz, mint az 5.36-os ábrán, ha -60dB/dekáddal metszi: a fázistöbblet biztosan negatív, ekkor a 180°-os vonal alatt megy el. A fenti példában -40dB/dekád meredekséggel a <math>\sqrt{2}</math> pontban metszi az x tengelyt a dB-es függvény, ezért a fázistöbbletet nem tudjuk meghatározni biztosan, a stabilitás határhelyzetében van. | ||
=== 10. Fázis-körfrekvencia görbe felrajzolása: === | |||
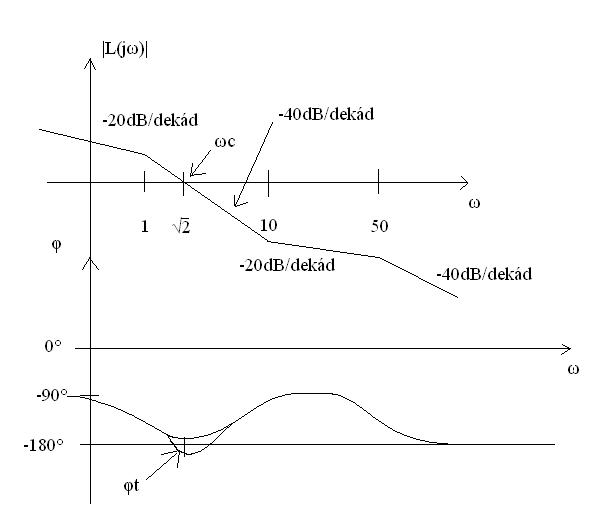
#'''Fázis-körfrekvencia görbe felrajzolása:''' <br/>[[Fájl:Bode-diagram fazis teljes.jpg]] | #'''Fázis-körfrekvencia görbe felrajzolása:''' <br/>[[Fájl:Bode-diagram fazis teljes.jpg]] | ||
=== 11. A rendszer stabilitásvizsgálata: === | |||
#'''Stabilis-e a rendszer:''' vagy azt nézed, hogy a fázistöbblet pozitív-e, vagy azt, hogy a jobboldali számsíkon van-e pólus: ha nincs, akkor stabilis. | #'''Stabilis-e a rendszer:''' vagy azt nézed, hogy a fázistöbblet pozitív-e, vagy azt, hogy a jobboldali számsíkon van-e pólus: ha nincs, akkor stabilis. | ||
=== 12. Statikus hiba: === | |||
#'''Statikus hiba:''' megnézed az integrátorok számát, az adja a típusszámot, és azt a sort írod le a táblázatból ''(Lásd: könyv 140. oldal)''. | #'''Statikus hiba:''' megnézed az integrátorok számát, az adja a típusszámot, és azt a sort írod le a táblázatból ''(Lásd: könyv 140. oldal)''. | ||
<br/> | <br/> | ||
| 31. sor: | 70. sor: | ||
*0 jelentése: hiba nélkül követi<br/> | *0 jelentése: hiba nélkül követi<br/> | ||
*<math>\infty</math> jelentése: nem tudja követni | *<math>\infty</math> jelentése: nem tudja követni | ||
[[Kategória:Infoalap]] | [[Kategória:Infoalap]] | ||
[[Kategória:Villanyalap]] | [[Kategória:Villanyalap]] | ||
A lap 2014. január 20., 19:56-kori változata
A Bode-diagram kézi rajzolása több tantárgyból is előjöhet. Ehhez nyújt segítséget az alábbi leírás, melyet Ndroo készített a Keviczky-féle Szabályozástechnika-könyv alapján.
A Bode-diagram készítésének lépései
1. Átviteli függvény átalakítása:
- Átviteli függvény átalakítása: Ha a feladatban ehhez hasonló alak van: , akkor át kell alakítani ilyen alakká: . Először a számlálót és a nevezőt is szorzattá kell alakítani, aztán annyit emelünk ki, hogy az s nélküli tagok értéke 1 legyen: . Így minden tényező alakú lesz; ha eleve így adták meg, akkor ezt a lépést ki kell hagyni.
2. Pólusok/zérusok felírása:
- Pólusok/zérusok felírása: Zérusok: azok a helyek ahol a számláló értéke 0 lesz, pólusok: azok a helyek, ahol a nevező értéke lesz 0. Minden szorzatalakra fel kell írni a következőt: , itt lesz a számláló/nevező értéke nulla, pl.: az egyik pólus, a többi: -nél, -nál van, a zérus: -nél van.
3. Fel/letörés:
- Fel/letörés: Ez az amplitúdó-körfrekvencia görbéhez kell (a dB-es). A pontok, ahol a görbe fel/letörik: alakból vagy s abszolútértéke, vagy értéke (a kettő abszolútértékben ugyanaz, úgy számold ki, ahogy jól esik). A görbe feltörik, ha zéruson megy át, ilyenkor a meredeksége 20dB/dekáddal nő (a függvény meredekéségét magasabbra rajzolod), illetve letörik, ha póluson megy át, a meredeksége itt 20dB/dekáddal csökken.
4. A görbe kezdő meredeksége:
- A görbe kezdő meredeksége: ezt az integrátorokból (szimpla s szorzótagok az átviteli függvényben) nézhető meg, ha nincs ilyen: a meredekség 0, a görbe vízszintesen indul, ha egy van (egyszeres integrátor): -20dB/dekád a kezdő meredekség, ha kettő van, azaz van (kétszeres integrátor): -40dB/dekád. A fenti példában egyszeres integrátor van, azaz -20dB/dekád a kezdő meredekség.
5. Az x tengely metszésének pontja:
- Az x tengely metszésének pontja: (vágási körfrekvencia, ): ezt a meredekség és az átviteli függvény szorzókonstansa (K) határozzák meg: ha a görbe meredeksége 0dB/dekád akkor nem metszi az x tengelyt (mert vízszintesen halad), ha -20dB/dekád, akkor K-nál metszi, ha -40dB/dekád, akkor -nál. Az egyes fel/letörések miatt úgy lehet nyomon követni, hol lesz a metszés helye, hogy megnézzük az integrátorokat/a kezdő meredekséget: ha K-ig nem változik a görbe meredeksége, akkor a meredekségnek megfelelően metszi (pl: egyszeres integrátor, K=5, ekkor -20dB/dekádos meredekséggel megy át az x tengelyen 5-nél), ha előtte megváltozik, akkor annak megfelelően (pl: kétszeres integrátor, K=16, 2-nél feltörik, ekkor 2-ig -40dB/dekád a meredekség, a tengelyt -nál metszené, de a feltörés miatt 2 után -20dB/dekáddal metszi az x tengelyt 16-nál.). A fenti példában K=2, egyszeres integrátor, -1-nél letörés van, ezért -40dB/dekád meredekséggel a pontban metszi.
6. Amplitúdó-körfrekvencia görbe felrajzolása:
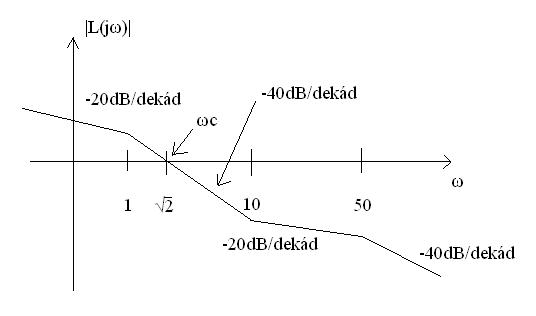
- Amplitúdó-körfrekvencia görbe felrajzolása: (Lásd: könyv 88. old.) Itt az eddigieket kell összegyúrni eggyé, előbb bejelölöd a pontokat, ahol történik valami, majd utána rajzolod meg a görbét, az y tengelyen , az x tengelyen értékével.
7. Fázisgörbe értéke:
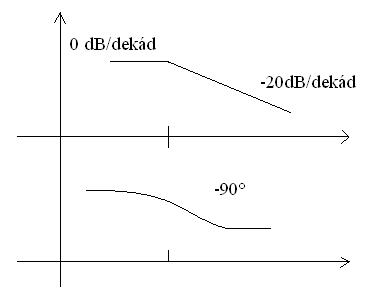
- Fázisgörbe értéke: (ez a másik görbe, a -s, rendes nevén: fázis-körfrekvencia görbe) a görbéhez képzeljünk el sávokat, ahol 90° a lépték az egyes értékek közt. A fenti fel/letöréseknek megfelelően változik, ha feltörik, akkor az érték nő 90°-al, ha letörik, akkor csökken 90°-al. Viszont ez nem egyik pillanatról a másikba megy végbe, hanem "átmenetszerűen", rajzban ez azt jelenti, hogy fel/letörésnél már félúton van az új állapot felé.
8. Fázisgörbe kezdőértéke:
- Fázisgörbe kezdőértéke: ez az integrátorok, és az átviteli függvény szorzókonstansán múlik:
- a konstans ha pozitív, akkor 0° a kezdőérték, ha negatív, akkor -180°
- az integrátor(ok) miatt 0-ban -90°-al jobban változik (-180°-al, ha kétszeres)
- ha a számlálóban volt egy szimpla s tag, akkor az 90°-al növeli.
- Pl: konstans negatív, egyszeres integrátor: -180°+(-90°)=-270°, konstans pozitív, számlálóban egy szimpla s: 0°+90°=90°. A fenti példában konstans pozitív, egyszeres integrátor: 0°-90°=-90°.
9. Fázistöbblet meghatározása:
- Fázistöbblet meghatározása: (Lásd: könyv 190-191. old) fázistöbblet fázis-körfrekvencia görbe értékének különbsége -180°-tól a vágási körfrekvenciánál. Azaz ahol a dB-es görbe metszi az x tengelyt, ott megnézed a -s görbe értéke mennyire tér el a -180°-os vonaltól. Ezt a meredekség határozza meg mekkora lesz: ha -20dB/dekáddal metszi az x tengelyt: a fázistöbblet biztosan pozitív (Lásd: könyv 191.old, 5.35 ábra), ha -40dB/dekáddal metszi: a fázistöbbletet nem lehet meghatározni biztosan, olyat rajzolsz, mint az 5.36-os ábrán, ha -60dB/dekáddal metszi: a fázistöbblet biztosan negatív, ekkor a 180°-os vonal alatt megy el. A fenti példában -40dB/dekád meredekséggel a pontban metszi az x tengelyt a dB-es függvény, ezért a fázistöbbletet nem tudjuk meghatározni biztosan, a stabilitás határhelyzetében van.
10. Fázis-körfrekvencia görbe felrajzolása:
11. A rendszer stabilitásvizsgálata:
- Stabilis-e a rendszer: vagy azt nézed, hogy a fázistöbblet pozitív-e, vagy azt, hogy a jobboldali számsíkon van-e pólus: ha nincs, akkor stabilis.
12. Statikus hiba:
- Statikus hiba: megnézed az integrátorok számát, az adja a típusszámot, és azt a sort írod le a táblázatból (Lásd: könyv 140. oldal).
| Típusszám | 0 | 1 | 2 |
| egységugrás | 0 | 0 | |
| sebességugrás | 0 | ||
| gyorsulásugrás |
- 0 jelentése: hiba nélkül követi
- jelentése: nem tudja követni