„Algoritmuselmélet - Vizsga, 2013.06.06.” változatai közötti eltérés
| 203. sor: | 203. sor: | ||
Ebből következik néhány dolog. Például az, hogy B legalább olyan nehéz probléma, mint A. Ha például B NP-teljes, akkor A is az. Ha B NP-nehéz, akkor A is az. Ha B coNP-beli, akkor A is az. Ez miért van? Hát azért, mert polinom időben át lehet alakítani az A problémát B-vé. Ezt indirekten könnyen lehet bizonyítani. Indirekt tegyük fel, hogy annak ellenére hogy B probléma NP-teljes és létezik egy olyan Karp-redukció ami A problmémát átalakítja B-vé, szóval mindezek ellenére A probléma P-beli. Ekkor A problémát egy polinom idejű f függvénnyel simán átalakítjuk B problémává, erről szól ugye a Karp-redukció. Ezek után ha bármikor B problémát akarnánk megoldani, akkor az f-függvény fordítva végrehajtásával a B inputját átalakítjuk A inputjává, megoldjuk az A problémát polinom időben, és kész is. Ez ellentmondás mivel B-ről azt mondtuk hogy NP-teljes. A másik érdekesség, hogy ha például egy NP-teljes vagy NP-nehéz problémáról kiderülne hogy P-beli, akkor az összes NP-beliről kiderülne hogy P-beli, mivel az NP-nehéz definíciója az, hogy legalább olyan nehéz mint bármely tetszőleges NP-beli. <br><br> | Ebből következik néhány dolog. Például az, hogy B legalább olyan nehéz probléma, mint A. Ha például B NP-teljes, akkor A is az. Ha B NP-nehéz, akkor A is az. Ha B coNP-beli, akkor A is az. Ez miért van? Hát azért, mert polinom időben át lehet alakítani az A problémát B-vé. Ezt indirekten könnyen lehet bizonyítani. Indirekt tegyük fel, hogy annak ellenére hogy B probléma NP-teljes és létezik egy olyan Karp-redukció ami A problmémát átalakítja B-vé, szóval mindezek ellenére A probléma P-beli. Ekkor A problémát egy polinom idejű f függvénnyel simán átalakítjuk B problémává, erről szól ugye a Karp-redukció. Ezek után ha bármikor B problémát akarnánk megoldani, akkor az f-függvény fordítva végrehajtásával a B inputját átalakítjuk A inputjává, megoldjuk az A problémát polinom időben, és kész is. Ez ellentmondás mivel B-ről azt mondtuk hogy NP-teljes. A másik érdekesség, hogy ha például egy NP-teljes vagy NP-nehéz problémáról kiderülne hogy P-beli, akkor az összes NP-beliről kiderülne hogy P-beli, mivel az NP-nehéz definíciója az, hogy legalább olyan nehéz mint bármely tetszőleges NP-beli. <br><br> | ||
Még egy fontos megjegyzés a Karp-redukcióhoz: ugye A problémát akarjuk megoldani, de csak B-t megoldó gépünk van. Az egyik gyakorlaton elhangzott, és fontos tudni, hogy a B-t megoldó gépet az A eldöntési probléma megoldásához csak EGYSZER használhatjuk. Azért mert a Karp-redukció az ilyen.<br><br> | |||
<big>'''(''Nem kérdezték, csak kieg.'') SAT probléma? '''<br><br></big> | <big>'''(''Nem kérdezték, csak kieg.'') SAT probléma? '''<br><br></big> | ||
A lap 2013. június 7., 17:50-kori változata
2013.06.06. vizsga megoldásai
1. Feladat (Van megoldás)
Ebben a feladatban a mélységi bejárással kapcsolatos kérdésekre kell válaszolni.
- (a) Adja meg a keresztél definícióját!
- (b) A mélységi bejárás során hogyan lehet a mélységi és a befejezési számok alapján felismerni a keresztéleket? Vizsgán megjegyzést fűztek hozzá: irányított gráfokra kell gondolni.
- (c) Bizonyítsa be, hogy irányítatlan gráf mélységi bejárásánál nincsenek keresztélek!
(a)
Tekintsük a G irányított gráf egy mélységi bejárását és a kapott T mélységi feszítő erdőt. Ezen bejárás szerint G egy x → y éle keresztél, ha x és y nem leszármazottjai egymásnak.
(b)
msz - mélységi szám
bsz - befejezési szám
Ha és , akkor az x → y egy keresztél.
Fájl:Keresztel 1.png
(c)
A b) rész alapján könnyen belátható. Ha lenne keresztél, az azt jelentené, hogy van olyan x → y él, amire fennáll, hogy és , vagyis y-ban előbb jártunk, mint x-ben, és y-nak van befejezési száma. Ennél fogva nem lehet keresztél, hiszen ha lenne, akkor y-ból eljuthattunk volna még x-be, mielőtt befejeztük volna.
Másképpen mondva: Nem fejezhettük volna be y-t anélkül, hogy ne jártunk volna x-ben.
2. Feladat
Milyen műveletek vannak a nyitott címzésű hash-elésnél? Hogyan kell megvalósítani a keresést, ha a nyitott címzésű hashelésnél kvadratikus maradék próbát használunk?
Nyitott címzésű hash-elés műveletei:
todo
(Nem kérdezték, csak kieg.) Mi az a nyitott címzésű hash-elés?
todo
(Nem kérdezték, csak kieg.) Mi az a kvadratikus maradék próba, nyitott címzésű hash-elésnél?
todo
keresés megvalósítása nyitott címzésű hash-elés esetén kvadratikus maradék próbánál:
3. Feladat
Adja meg az UNIÓ-HOLVAN adatszerkezet definícióját! (A fákkal való implementálást nem kell leírnia.) Mutassa meg, hogy mikor és hogyan használjuk az UNIÓ és a HOLVAN műveleteket a Kruskal algoritmusban!
UNIÓ-HOLVAN adatszerkezet definíciója:
todo
(Nem kérdezték, csak kieg.) Mi az a Kruskal algoritmus?
todo
Mikor és hogyan használjuk az UNIÓ és a HOLVAN műveleteket a Kruskal algoritmusban:
4. Feladat
Pista bácsi fel akar ugrálni egy n hosszú, fekete illetve fehér fokokból álló csigalépcsőn. Legfeljebb k fokot tud ugrani, de arra vigyáznia kell, hogy páros (>=2) sok foknyi ugrás után páratlan sokat és páratlan sok után mindig páros (>=2) sokat ugorjon. Adjon O(nk) lépésszámú algoritmust, amely megmondja, hogy fel tud-e úgy ugrálni a csigalépcső tetejére, hogy csak egyféle színű lépcsőfokot használ. (A lépcső fokai rendszertelenül vannak színezve, a színezést ismerjük.) Vizsgán megjegyzést fűztek hozzá: a talaj és a legteteje nem színes, csak a lépcsők; csak fölfele (előrefele) ugrál, visszafele nem.
todo
5. Feladat (Van megoldás)
A hátizsák probléma órán tanult algoritmusát futtattuk egy konkrét inputon, melyben 3 tárgy szerepel. Mi lehetett ez a konkrét input, ha az alábbi táblázat keletkezett?
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 10 | 10 | 10 | 10 |
| 2 | 0 | 0 | 5 | 5 | 10 | 10 | 15 | 15 |
| 3 | 0 | 0 | 5 | 5 | 13 | 13 | 18 | 18 |
Az egyszerűség kedvéért a súly legyen kg, az érték pedig €.
- Az első sor alapján az 1-es csomag értéke €10, súlya 4kg.
- A második sor alapján a 2-es csomag értéke €5, súlya 2kg.
- A 3. sornál kicsit rafkósnak kell lenni. Leírhatnám egyből a megoldást, de talán több értelme van, ha a logikai zsákutcákat is leírom.
- Először gondolhatnánk arra, hogy a [4,3]-as cella 10+3 formában áll elő, így a 3-as csomag értéke €3. Viszont így a súlyának 0kg-nak kéne lennie, ami nyílván fatal error.
- Második gondolatunk az lehetne, hogy akkor 5+8 formában áll elő, így a 3-as csomag értéke €8. Súlya ekkor 2kg kellene legyen, viszont akkor a [2,3]-as cellába 8-nak, és nem 5-nek kéne szerepelnie, tehát ez se jó megoldás.
- Harmadik ötletnek nagyon más nem jöhet szóba, hogy akkor a 3-as csomag értéke €13, súlya pedig 4kg. És ha leellenőrizzük, látszik, hogy ez lesz a jó megoldás.
Tehát végeredményben a megoldás:
- 1-es csomag (€10, 4kg)
- 2-es csomag (€5, 2kg)
- 3-as csomag (€13, 4kg)
6. Feladat (Van megoldás)
Egy irányítatlan, élsúlyozott gráf az alábbi éllistával adott (zárójelben az élsúlyok):
- (a) Mi lehet x és y értéke, ha tudjuk, hogy az élsúlyok egész számok, és azt is tudjuk, hogy a B csúcsból indított Prim algoritmus az alábbi sorrendben vette be az értékeket: BE, ED, BA, BC. Vizsgán megjegyzést fűztek hozzá: az élsúlyok pozitív egész számok, a pozitív szót kifelejtették véletlenül.
- (b) Mely éleket és milyen sorrendben választja ki a Kruskal algoritmus? (Ha több megoldás is van, akkor az összeset adja meg!)
a) Prim algoritmus - Ugyebár úgy dolgozik, hogy az aktuális fához a vele szomszédos élek közül a legkisebb súlyút veszi be. Prim: BE → ED → BA → BC
- A fához hozzáadjuk a BE élt.
- Most az ED élt választottuk. Ez alapján x értéke csak 1 lehet, így . (Feladatból kihagyták, hogy pozitív egészekről van szó, amúgy lehetne.)
- Most az AB élt adjuk hozzá, ez alapján .
- Most a BC élt adjuk hozzá, ez alapján , így végül .
b) Kruskal algoritmus - Éleket nagyság szerint sorrendbe rakjuk, és növekvő sorrendben felvesszük a fához az éleket, vigyázva, hogy ne csináljunk kört.
1 súlyú - AB, BE, ED
2 súlyú - AE
3 súlyú - BC, AD, EC (és DC, ha )
Az összes megoldás:
- Az 1 súlyú éleket féleképpen veheti fel az algoritmus (nem lehet belőlük kört csinálni, így itt nincsen para).
- Utána megpróbálná felvenni az AE élt, de azzal egy kört kapna, így nem veszi fel. Az AD éllel szintén így járna (~ezeket kéne pirosra színezni, ha olyan lenne a feladat).
- Maradtak a BC, EC és DC oldalak.
- Ha , akkor ezeket szintén 6 féleképpen veheti fel, tehát összesen 36 féleképpen futhat az algoritmus.
- Ha , akkor a DC oldal kiesik, a maradék 2 élt 2 féleképpen veheti fel, így 12 féleképpen futhat az algoritmus.
7. Feladat
Létezik-e olyan X eldöntési probléma, amire X∉NP és X≺SAT egyszerre fennáll?
(Nem kérdezték, csak kieg.) NP osztály?
A problémáknak lehet több típusú több bemenete, és több típusú több kimenete. Ezeket átfogalmazzuk olyanra, hogy a kimenete egyetlen bit legyen (IGEN / NEM), mert ezen algoritmusok felhasználásával is teljesen jól lehet dolgozni, ugyanakkor könnyebb őket nehézség / bonyolultság szerint osztályozni. Az ilyen 1 bites kimenetű problémákat nevezzük eldöntési problémáknak.
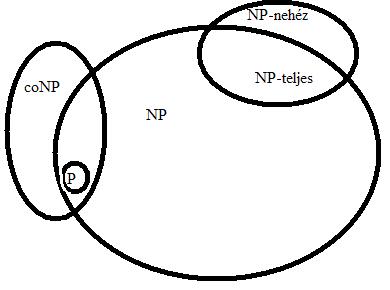
Az eldöntési problémákat nehézség / bonyolultság szerint osztályokba soroljuk, ezen osztályok között olyan kapcsolatok vannak mint a halmazoknál; ez a fenti rajzon látszik.
A P osztályba olyan problémák tartoznak, amelyekre ismert olyan algoritmus, ami a bemenet polinomjával megadott idő alatt lefut. Vagyis ha a bemenet n, akkor az algoritmusra azt mondjuk, hogy nagy_ordó(valami), ahol a valami n egy polinomja, például n négyzet, n köb, három n négyzet meg négy meg nyolc n köb, és ilyesmik.
Az NP osztályba olyan problémák tartoznak, amelyekre (jelenleg) nem ismert polinom idejű (P-beli) algoritmus, de igen válasz esetén létezik hatékony tanúsítvány. Vagyis, adott egy nagy csomó bemenet és van egy kérdés. P-idő alatt nem tudjuk megmondani a választ, de ha valaki megsúgja hogy a válasz IGEN, akkor P-időben meg tudjuk mondani, hogy ez hülyeség vagy nem hülyeség. Ha azt súgják meg hogy NEM, akkor fogalmunk sincs, P-időben nem tudjuk eldönteni hogy hülyeség-e vagy sem. (Ha így lenne, vagyis igen és nem válasz esetén is P-időben ellenőrizni tudnánk a válasz helyességét, akkor az egész probléma P-beli lenne, hiszen megsúgjuk saját magunknak hogy NEM és ha helyes akkor NEM egyébként igen. Persze ha az IGEN-ről P-időben kiderül hogy hülyeség attól még lehet hogy IGEN, csak éppen nem az a konkrét ami meg lett súgva, hanem egy másik.)
A coNP osztály lényegében ugyanaz mint az NP osztály, csak NEM válaszra. Vagyis (jelenleg) nem ismerünk rá P-beli algoritmust, de ha a válasz NEM, akkor P-időben (hatékonyan) ellenőrizni tudjuk, hogy ez-e a jó válasz vagy sem. Szintén, IGEN válasz esetén semmit sem tudunk mondani P-időben, a fenti okok miatt (ami a zárójelben van).
Az NP nehéz osztályba tartozó eldöntési problémák közül bármelyik legalább olyan nehéz, mint bármelyik másik NP-beli eldöntési probléma. Itt jön képbe a Karp-redukció fogalma. Jó dolog sok NP nehéz problémát ismerni, mert akkor ha találunk egy problémát, akkor ha találunk olyan Karp-redukciót, ami azt mutatja, hogy ez a probléma visszavezethető egy közismert NP nehéz problémára, akkor a mi ismeretlen problémánk is NP nehéz lesz. Ez azért van, mert a Karp-redukció tranzitív művelet, továbbá a Karp-redukcónál használt f függvény P-beli, amit kétszer egymás után alkalmazva is még mindig P-beli lesz ez a dolog (az inputok átalakítása).
Az NP teljes problémák azok, amik NP nehezek és NP-beliek is egyszerre. A fenti dolog ide is érvényes, vagyis jó dolog ha sok nevezetes NP teljes problémát ismerünk, mert ha egy ismeretlen problémához találunk egy olyan Karp-redukciót, ami alapján az ismeretlen problémánkat visszavezethetjük egy közismert NP teljes problémára, akkor az ismeretlen problémánkról is kiderült, hogy NP teljes.
(Nem kérdezték, csak kieg.) Karp-redukció?
Van egy olyan gépünk, ami kizárólag B problémát tudja megoldani. Nekünk viszont A problémánk van. Ekkor ha szerencsénk van, akkor fogunk találni egy olyan Karp-redukciót, hogy A≺B. Ennek persze vannak feltételei. Az A eldöntési probléma inputját át kell alakítani B eldöntési probléma inputjává, és meg is kell adni ezt a függvényt, nevezzük el ezt a függvényt f függvénynek. Feltétel, hogy f függvény polinom időben kiszámolható legyen, és ezt be is kell bizonyítani. Továbbá azt is be kell bizonyítani, hogy amennyiben a normális inputra A azt válaszolná, hogy IGEN, akkor az f(normális input)-ra a B szintén ugyanezt válaszolná (és ugyanezt be kell bizonyítani NEM válaszra is). Magyarul a B dolgot megoldó gépet megerőszakoljuk hogy A problémát is hajlandó legyen megoldani.
Ebből következik néhány dolog. Például az, hogy B legalább olyan nehéz probléma, mint A. Ha például B NP-teljes, akkor A is az. Ha B NP-nehéz, akkor A is az. Ha B coNP-beli, akkor A is az. Ez miért van? Hát azért, mert polinom időben át lehet alakítani az A problémát B-vé. Ezt indirekten könnyen lehet bizonyítani. Indirekt tegyük fel, hogy annak ellenére hogy B probléma NP-teljes és létezik egy olyan Karp-redukció ami A problmémát átalakítja B-vé, szóval mindezek ellenére A probléma P-beli. Ekkor A problémát egy polinom idejű f függvénnyel simán átalakítjuk B problémává, erről szól ugye a Karp-redukció. Ezek után ha bármikor B problémát akarnánk megoldani, akkor az f-függvény fordítva végrehajtásával a B inputját átalakítjuk A inputjává, megoldjuk az A problémát polinom időben, és kész is. Ez ellentmondás mivel B-ről azt mondtuk hogy NP-teljes. A másik érdekesség, hogy ha például egy NP-teljes vagy NP-nehéz problémáról kiderülne hogy P-beli, akkor az összes NP-beliről kiderülne hogy P-beli, mivel az NP-nehéz definíciója az, hogy legalább olyan nehéz mint bármely tetszőleges NP-beli.
Még egy fontos megjegyzés a Karp-redukcióhoz: ugye A problémát akarjuk megoldani, de csak B-t megoldó gépünk van. Az egyik gyakorlaton elhangzott, és fontos tudni, hogy a B-t megoldó gépet az A eldöntési probléma megoldásához csak EGYSZER használhatjuk. Azért mert a Karp-redukció az ilyen.
(Nem kérdezték, csak kieg.) SAT probléma?
todo
A feladat megoldása:
8. Feladat
P-ben van vagy NP-teljes az alábbi eldöntési probléma:
- Input: irányítatlan G gráf
- Kérdés: Igaz-e, hogy G-ben vagy van Hamilton-út vagy G 3 színnel színezhető?
(Nem kérdezték, csak kieg.) P osztály?
todo
(Nem kérdezték, csak kieg.) NP-teljes osztály?
todo
(Nem kérdezték, csak kieg.) H-út?
todo
(Nem kérdezték, csak kieg.) 3 színnel színezhetőség problémája?
todo
A feladat megoldása: