„Mikroökonómia alapfogalmak” változatai közötti eltérés
Pár új fogalom a jegyzetből |
a Halott sablon eltávolítása |
||
| (5 közbenső módosítás, amit 5 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
{{Vissza|Mikro- és makroökonómia}} | {{Vissza|Mikro- és makroökonómia}} | ||
==Keresleti és kínálati függvény== | ==Keresleti és kínálati függvény== | ||
Egy mennyiség (Q, x tengely) – ár (p, y tengely) koordinátarendszerben ábrázolt (általában) lineáris függvény a keresleti és a kínálati függvény is. A keresleti függvény mindig csökkenő, jele D. A kínálati függvény mindig növekvő, jele S. (Kivétel: | Egy mennyiség (Q, x tengely) – ár (p, y tengely) koordinátarendszerben ábrázolt (általában) lineáris függvény a keresleti és a kínálati függvény is. A keresleti függvény mindig csökkenő, jele D. A kínálati függvény mindig növekvő, jele S. (Kivétel: [https://hu.wikipedia.org/wiki/Giffen-javak Griffen javak]) Ha a két függvényt egyszerre ábrázoljuk egy közös koordinátarendszerben, akkor Marshall-keresztről beszélünk. | ||
Például egy termék piaci keresleti függvénye: Q = 400-2p, a kínálati függvénye: Q = p-20. | Például egy termék piaci keresleti függvénye: Q = 400-2p, a kínálati függvénye: Q = p-20. | ||
| 27. sor: | 26. sor: | ||
A fogyasztói többlet (FT) a keresleti függvény és az ár, mint konstans függvény közé eső terület. Mivel órán a keresleti függvény mindig lineáris függvény, ez egy egyszerű háromszög területszámítása. | A fogyasztói többlet (FT) a keresleti függvény és az ár, mint konstans függvény közé eső terület. Mivel órán a keresleti függvény mindig lineáris függvény, ez egy egyszerű háromszög területszámítása. | ||
Például az előző Q=400-2p keresleti függvény és p=140 illetve Q=120 egyensúlyi árral és mennyiséggel egy ( | Például az előző Q=400-2p keresleti függvény és p=140 illetve Q=120 egyensúlyi árral és mennyiséggel egy (400-140) és 120 befogókkal rendelkező háromszöget kapunk, így FT=280*120/2=15600. | ||
==Termelői többlet== | ==Termelői többlet== | ||
[[File:mikmak_fttt_20190603.png|right|350px]] | |||
A termelői többlet (TT) az ár és a kínálati függvény közé eső terület. Ez megint egy lineáris és egy konstans függvény által meghatározott háromszög. | A termelői többlet (TT) az ár és a kínálati függvény közé eső terület. Ez megint egy lineáris és egy konstans függvény által meghatározott háromszög. | ||
Például az előző Q=p-20 kínálati függvény és p=140, Q=120 adatokkal egy (140-20) és 120 befogókkal rendelkező háromszöget kapunk, így TT=120*120/2=7200. | Például az előző Q=p-20 kínálati függvény és p=140, Q=120 adatokkal egy (140-20) és 120 befogókkal rendelkező háromszöget kapunk, így TT=120*120/2=7200. | ||
| 43. sor: | 47. sor: | ||
<math> | <math> | ||
\epsilon = \frac{\Delta Q \%}{\Delta p \%} = \frac{Q_2 - Q_1}{p_2 - p_1} \cdot \frac{p_1 + p_2}{Q_1 + Q_2} | \epsilon = \frac{\Delta Q \%}{\Delta p \%} = \frac{Q_2 - Q_1}{p_2 - p_1} \cdot \frac{p_1 + p_2}{Q_1 + Q_2} | ||
</math> | </math> - ívrugalmasság | ||
<math> | |||
\epsilon_P^Q = \frac{\delta Q}{\delta p} \cdot \frac{p}{Q} = Q'(p) \cdot \frac{p}{Q} | |||
</math> - pontrugalmasság | |||
* | * ϵ > 0 paradox árhatás, Giffen javak | ||
* =0 Tökéletesen rugalmatlan kereslet | * ϵ = 0 Tökéletesen rugalmatlan kereslet | ||
* <1 Rugalmatlan kereslet (ár nő, összbevétel nő) | * |ϵ| < 1 Rugalmatlan kereslet (ár nő, összbevétel nő) | ||
* =1 Egységnyi rugalmasság (maximális bevétel) | * |ϵ| = 1 Egységnyi rugalmasság (maximális bevétel) | ||
* >1 Rugalmas kereslet (ár nő, bevétel csökken) | * |ϵ| > 1 Rugalmas kereslet (ár nő, bevétel csökken) | ||
==Giffen javak== | ==Giffen javak== | ||
A lap jelenlegi, 2024. október 28., 17:38-kori változata
Keresleti és kínálati függvény
Egy mennyiség (Q, x tengely) – ár (p, y tengely) koordinátarendszerben ábrázolt (általában) lineáris függvény a keresleti és a kínálati függvény is. A keresleti függvény mindig csökkenő, jele D. A kínálati függvény mindig növekvő, jele S. (Kivétel: Griffen javak) Ha a két függvényt egyszerre ábrázoljuk egy közös koordinátarendszerben, akkor Marshall-keresztről beszélünk.
Például egy termék piaci keresleti függvénye: Q = 400-2p, a kínálati függvénye: Q = p-20.
Egyensúlyi ár
Egyensúlyi árról beszélünk, ahol a keresleti és kínálati függvény metszi egymást. Az egyensúlyi árhoz tartozik egy egyensúlyi mennyiség is.
Például az előző Q=400-2p és Q=p-20 függvényekhez a p=140 egyensúlyi ár és Q=120 egyensúlyi mennyiség tartozik.
Kereslet
Az a termék és szolgáltatásmennyiség, amelyet a fogyasztók adott időpontban, adott piaci feltételek mellett képesek és hajlandók megvásárolni. Keresleten mindig fizetőképes keresletet értünk, vagyis olyan vásárlói szándékot, amely mögött megfelelő pénzösszeg áll.
Kínálat
Az a termék- és szolgáltatás mennyiség, amelyet a vállalatok adott időpontban az adott piaci feltételek mellett képesek és hajlandók eladni.
Túlkínálat
Egy adott pontban túlkínálat van, ha a kínálati függvény értéke nagyobb, mint a keresleti függvényé. (Azaz többet kínálnak, mint keresnek). A piaci ár csökkenni fog, amíg el nem éri az egyensúlyi árat.
Túlkereslet
Egy adott pontban túlkereslet van, ha a keresleti függvény értéke nagyobb, mint a kínálati függvényé. (Azaz többet keresnek, mint kínálnak). A piaci ár növekedni fog, amíg el nem éri az egyensúlyi árat.
Fogyasztói többlet
A fogyasztói többlet (FT) a keresleti függvény és az ár, mint konstans függvény közé eső terület. Mivel órán a keresleti függvény mindig lineáris függvény, ez egy egyszerű háromszög területszámítása.
Például az előző Q=400-2p keresleti függvény és p=140 illetve Q=120 egyensúlyi árral és mennyiséggel egy (400-140) és 120 befogókkal rendelkező háromszöget kapunk, így FT=280*120/2=15600.
Termelői többlet
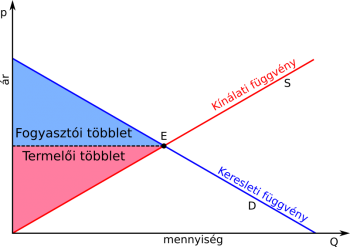
A termelői többlet (TT) az ár és a kínálati függvény közé eső terület. Ez megint egy lineáris és egy konstans függvény által meghatározott háromszög.
Például az előző Q=p-20 kínálati függvény és p=140, Q=120 adatokkal egy (140-20) és 120 befogókkal rendelkező háromszöget kapunk, így TT=120*120/2=7200.
Holtteherveszteség
Az árak minimalizálása, maximalizálása vagy adóztatása esetén jelenik meg.

Árrugalmasság
A kereslet árrugalmassága megmutatja, hogy hány %-kal változik a kereslet, ha az ár 1%-kal változik. Általában negatív érték az eredmény, ami azt jelenti, hogy az ár növekedésével kevesebbet fogunk fogyasztani.
- ívrugalmasság
- pontrugalmasság
- ϵ > 0 paradox árhatás, Giffen javak
- ϵ = 0 Tökéletesen rugalmatlan kereslet
- |ϵ| < 1 Rugalmatlan kereslet (ár nő, összbevétel nő)
- |ϵ| = 1 Egységnyi rugalmasság (maximális bevétel)
- |ϵ| > 1 Rugalmas kereslet (ár nő, bevétel csökken)
Giffen javak
Abban az esetben, ha az árrugalmasság pozitív, Giffen javakról beszélünk.
Ilyen például a kenyér: ha drágul a kenyér, a szegényebb családok nem engedhetik meg maguknak a drágább ételeket, így kenyérből fognak többet fogyasztani
Kereszt-árrugalmasság
A számítása ugyanúgy működik, mint az árrugalmasságnak, de itt nem önmagához, hanem egy másik termékhez viszonyítjuk. Ha pozitív, akkor a két termék helyettesíti egymást. Ha negatív, akkor kiegészíti egymást.
Jövedelem
A gazdasági szereplők termelési, illetve fogyasztási döntéseik során a jövedelmet, mint választási lehetőségeiket korlátozó tényezőt veszik számba.
Nomináljövedelem
Egy adott időszakban a gazdasági szereplő által realizált pénzösszeg
Reáljövedelem
Az az árumennyiség, amennyit a gazdasági szereplő a nomináljövedelméből vásárolni tudna.
Jövedelemrugalmasság
Hasonlóan az előzőekhez, csak itt nem az árat, hanem a jövedelmet kell figyelembe venni és arra ad egy számot, hogy nagyobb fizetéskor hogy fog fogyni egy termék. Például nagyobb jövedelemnél az S-Budget májkrém helyett jobb minőségűt veszünk, tehát az S-Budget májkrém kereslete csökkenni fog.
Termelési függvény
A termelési függvény azt mondja meg, hogy ha hatékonyan alkalmazzuk az erőforrásokat, akkor mennyit tudunk termelni. Rövid távú termelési függvényeknél a munkát szoktuk változónak hagyni, és az összes többi erőforrást fixnek választjuk. Hosszabb távú termelési függvénynél minden egyéb tényező is változhat.
Átlagtermék
Az átlagtermék (AP) megmutatja, hogy egy tényező mekkora mennyiséget állít elő átlagosan. A termelési függvényt egyszerűen leosztjuk a változóval.
Határtermék
A határtermék (MP) megmutatja, hogy az utolsó erőforrásváltozás mennyivel módosította a termelést. Itt a termelési függvény változását kell leosztani a tényező változásával.
Isoquant
Olyan görbe, ahol a termelési függvény értéke fix. Itt lehet jól kielemezni, hogy milyen tényezőből érdemes többet szerezni.
Teljes költség
A teljes költség (TC) megmutatja, hogy az adott kibocsátáshoz szükséges ráfordítás mennyibe került a vállalatnak. Felbontható fix és változó költségre.
Fix költség
A fix költség (FC) megmutatja, hogy a fix tényező ráfordítása mennyibe került a vállalatnak.
Változó költség
A változó költség (VC) megmutatja, hogy a termeléshez szükséges változó tényezők ráfordításának mekkora a költsége.
Határköltség
A határköltség (MC) megmutatja, hogy egy pótlólagos termékmennyiség előállítása mennyivel változtatná meg az összköltséget/változó költséget. A teljes költség deriváltja.
Átlagos költségek
A fenti költségek egy darabra levetített értéke (azaz q-val osztunk). Jelei AC, AFC, AVC attól függően, melyik költséget vetítjük le.
Profitmaximalizáló vállalat
A profitmaximalizáló vállalat annyit termel, hogy a határköltség megegyezzen a határbevétellel (azaz a határprofit 0): MR=MC. Tökéletes verseny esetén MR=p.
Fedezeti pont
Fedezeti pont: az a piaci ár, amely esetében a vállalat bevételei éppen fedezik az összes költséget, azaz a profit nulla.
Üzemszüneti pont
Üzemszüneti pont: az a piaci ár, ami alatt már érdemes bezárni az üzletet és beszüntetni a termelést. Ha pl. rövidtávon negatív a profit, viszont a fix költségeket a termeléssel fedezik, akkor nem éri meg leállni.
Jövőérték
Jelenlegi pénzünk értéke t idő múlva r kamatláb mellett.
Jelenérték
Jövőérték ellentettje: ha t idő múlva kapunk egy fix hozamot, az ennyit érne most.
Tökéletes verseny
Sok a piaci szereplő, a piaci belépésnek nincs akadálya, nem különböztetik meg a terméket gyártó alapján.
Monopolisztikus verseny
Szabad a belépés a versenyre, de kevés a piaci szereplő. A termelők termékei kis mértékben különböznek (próbálnak kiemelkedni).
Oligopólium
Kevés a piaci résztvevő, a cégek marketingmunkát folytatnak, reagálnak egymás lépéseire.
Monopólium
Egyedül van a piacon, befolyásolni tudja a termék árát.
Transzformációs ráta
Azt méri, hogy az egyik termékcsoport mennyiségének egységnyi növelése érdekében a másik termékcsoport hány egységéről kell lemondani. Az egyik termék ily módon elveszített mennyisége egyben a másik termék mennyiségének növelésével járó költsége, vagyis az alternatív költség.
Határelemzés
Az a megközelítés, amikor a gazdasági szereplők mindig egy adott döntéssel együtt járó pótlólagos hasznokat és pótlólagos költségeket mérlegelik, és ezeket összehasonlítva döntenek.
Termelői (kínálati) rezervációs ár
Az a legalacsonyabb ár, amelyért a termelők hajlandók megtermelni és eladásra felkínálni valamely jószágot.
Technikai hatékonyság
Technikailag hatékonyak azok a termelési eljárások, amelyek egyik inputtényezőből sem használnak fel felesleges mennyiséget.
Gazdasági hatékonyság
Gazdaságilag hatékony az az eljárás, amelyik az adott kibocsátást a lehető legkisebb költségekkel valósítja meg ill. adott költségszint mellett a legnagyobb kibocsátást biztosítja.
Optimális üzemméret
A hosszú távú átlagköltség függvény minimuma. Ennél a termelési mennyiségnél az átlagköltség mind rövid, mind hosszú távon a legkisebb.
Származékos kereslet
A termelési tényezők iránti kereslet úgynevezett származékos kereslet, mert a termelési tényezők felhasználásával előállítható termékek iránti kereslet miatt létezik. Ha a mögöttes áruk kereslete nő, a származékos kereslet is nőni fog!
